当前位置：文档之家 › 计量经济学 第三章 基本回归模型.

计量经济学 第三章 基本回归模型.

  • 格式：ppt
  • 大小：661.50 KB
  • 文档页数：73

下载文档原格式

  / 73

合集下载

计量经济学第三章多元线性回归模型

计量经济学第三章多元线性回归模型

⒈零均值假定
E( i) 0 i 1,2,, n
E(U) 0
⒉同方差和无自相关假定
COV (i , j ) E(i E(i ))( j E( j ))
2 i j

E(i
j
)


0
i j
VAR(U ) E(U E(U))(U E(U))
Yˆi ˆ1 ˆ2 X 2i ˆK X Ki
i 1,2,, n
Yi Yˆi ei
Yˆi

ˆ j
E(Y
j
X 2i ,,
X Ki
)
注意：β1一般情况下没有明确的经济含义，但一般 总包含在回归模型中。
3.1多元线性回归模型及古典假定
二、多元线性回归模型的矩阵形式
总体回归函数描述了一个被解释变量与多个解释
变量之间的线性关系，线性是针对参数而言的。
其中， j 为偏回归系数，表示：在控制其他变量 不变的条件下，第j个解释变量的单位变动对被解释 变量平均值的影响。
j

Y X j(保持其他变量不变)

Y X j
3.1多元线性回归模型及古典假定
样本回归函数：
(XX)1 X 2ΙX(XX)1 2 (XX)1 XX(XX)1 2 (XX)1
i 1
ei 0





N
( ei2 )
i 1
ˆ2
N

2
N i 1
(Yi
ˆ1

ˆ2 X 2i
ˆK
X Ki ) X 2i

2
ei X 2i 0
偏 导

第三章多元线性回归模型(计量经济学,南京审计学院)

第三章多元线性回归模型(计量经济学,南京审计学院)

Yˆ 116.7 0.112X 0.739P
R2 0.99
(9.6) (0.003) (0.114)
Y和X的计量单位为10亿美元 (按1972不变价格计算).
P
食品价格平减指数 总消费支出价格平减指数
100，（1972
100）
3
多元线性回归模型中斜率系数的含义
上例中斜率系数的含义说明如下： 价格不变的情况下，个人可支配收入每上升10
c (X X )1 X D
从而将 的任意线性无偏估计量 * 与OLS估计量 ˆ 联系
起来。
28
cX I
由
可推出：
(X X )1 X X DX I
即 I DX I
因而有 D X 0
cc (X X )1 X D (X X )1 X D ( X X )1 X D X ( X X )1 D
第三章 多元线性回归模型
简单线性回归模型的推广
1
第一节 多元线性回归模型的概念
在许多实际问题中，我们所研究的因变量的变动 可能不仅与一个解释变量有关。因此，有必要考虑线 性模型的更一般形式，即多元线性回归模型：
Yt β0 β1X1t β2 X 2t ... βk X kt ut t=1,2,…,n
Yt
ˆ0
βˆ 1
X
1t
... βˆ K X Kt
2
为最小，则应有：
S
S
S
ˆ0 0, ˆ1 0, ..., ˆ K 0
我们得到如下K+1个方程（即正规方程）：
13
β0 n
β1 X1t ...... β K X Kt Yt
β 0 X 1t β1 X 1t 2 ...... β K X 1t X Kt X 1tYt

第3章 多元线性回归模型 《计量经济学》PPT课件

第3章 多元线性回归模型 《计量经济学》PPT课件

于是：
βˆ
ˆ1 ˆ 2
0.7226 0.0003
0.0003 1.35E 07
15674 39648400
01.0737.71072
⃟ 正规方程组 的另一种写法
对于正规方程组 XY XXβˆ
XXβˆ Xe XXβˆ
于是 Xe 0 (*)
或
ei 0
(**)
X jiei 0
i
(*) 或（ ** ）是多元线性回归模型正规方程 组的另一种写法。
第三章 经典单方程计量经济学模型： 多元线性回归模型
• 多元线性回归模型 • 多元线性回归模型的参数估计 • 多元线性回归模型的统计检验 • 多元线性回归模型的预测 • 回归模型的其他形式
§ 3. 1 多元线性回归模型
一、多元线性回归模型 二、多元线性回归模型的基本假定
一、多元线性回归模型
多元线性回归模型 : 表现在线性回归模型 中的解释变量有多个。
的秩 =k+1 ，即 X 满秩。
假设 2. 随机误差项零均值，同方差。
0
0
0
E
(μ
μ
)
E
1
n
1
n
E
12
n 1
1 n
2 n
var(1 ) cov(1, n ) 2 0
2I
cov(
n
,
1
)
var(n )
0
2
i E(i )
βˆ (xx)1 xY
ˆ0 Y ˆ1 X 1 ˆk X k
⃟ 随机误差项的方差的无偏估计
可以证明，随机误差项的方差的无偏 估计量为：
ˆ 2
ei2 n k 1
ee n k 1

计量经济学第三章-回归模型的扩展

计量经济学第三章-回归模型的扩展
验的结果，或直接取成 1/|ei|、1/ei2
第二节 自相关性
一Байду номын сангаас自相关性的概念及其产生原因：
1.定义：随机误差项的各期值之间存在相关性 COV(t, s)0, ts
例：投资函数、生产函数
2.产生原因： 1)模型遗漏了自相关的解释变量； 2)模型函数形式的设定误差； 3)经济惯性； 4)随机因素影响； （注：自相关性更易产生于时序数据）
原理：辅助回归检验 命令：View\ResidualTest \SerialCorrelation LM
Test
四、自相关性的修正方法
1.利用广义差分变换消除自相关性：
步骤： 实质：GLS估计
2.的估计方法：
1）近似估计； 2）迭代估计；
3.Eviews软件的实现：
1）检验自相关性的阶数； 2）在LS命令中增加AR项；
二、异方差的影响
1.OLS估计不再是最佳估计量； 2.T检验可靠性降低； 3.增大预测误差； 三、异方差的检验 ★1.图形分析： (1)观察Y、X相关图：SCAT Y X (2)残差分析:观察回归方程的残差图
在方程窗口直接点击Residual按钮； 或：点击View\Actual,Fitted,Residual\Table
1. 调整季节波动
y a bx 1D1 2D2 3D3
2. 检验模型结构的稳定性（P141）
y a bx D XD
3. 混合回归
例8．教材P132
第五节 滞后变量模型
一、滞后效应与滞后变量的作用 1、产生滞后效应的原因：
1)心理因素：消费习惯、消费心理（如价格、利率） 2)技术原因：农民收入、农产品价格、天气条件 3)制度原因：

第三章 一元线性回归模型

第三章 一元线性回归模型

第三章一元线性回归模型第一节一元线性回归模型及其基本假设一元线性回归模型第二章回归分析的基本思想指出，由于总体实际上是未知的，必须根据样本回归模型估计总体回归模型，回归分析的目的就是尽量使得样本回归模型接近总体回归模型，那么采取什么方法估计样本回归模型才使得估计出的样本回归模型是总体回归模型的一个较好估计值呢？这里包括两个问题：一是采用什么方法估计样本回归模型；二是怎样验证估计出的样本回归模型是总体回归模型的一个较好估计值。

这些将在接下来的内容中讲到。

这一章介绍最简单的一元线性回归模型，下一章再扩展到多元线性回归模型。

一元线性回归模型及其基本假设一、一元线性回归模型的定义一元线性回归模型是最简单的计量经济学模型，在该一元模型中，仅仅只含有一个自变量，其一般形式为：yi = β0 + β1xi + μi（3.1.1）其中yi是因变量，xi是自变量，β0、β1是回归参数，μi是随机项。

由于式（3.1.1）是对总体而言的，也称为总体回归模型。

随机项μ代表未被考虑到模型中而又对被解释变量y有影响的所有因素产生的总效应。

二、一元线性回归模型的基本假设由于模型中随机项的存在使得参数β0和β1的数值不可能严格计算出来，而只能进行估计，在计量经济学中，有很多方法可以估计出这些参数值，但采用什么方法能够尽可能准确地估计出这些参数值，取决于随机项μ和自变量x的性质。

因此，对随机项μ和自变量x的统计假定以及检验这些假定是否满足的方法，在计量经济学中占有重要的地位。

估计方法中用得最多的是普通最小二乘法（Ordinary Least Squares），同样为了保证利用普通最小二乘法估计出的参数估计量具有良好的性质，也需要对模型的随机项μ和自变量x 提出若干种假设。

当模型中的随机项μ和自变量x满足这些假设时，普通最小二乘法就是适合的估计方法；当模型中的随机项μ和自变量x不满足这些假设时，普通最小二乘法就不是适合的方法，这时需要利用其他的方法来估计模型。

计量经济学-3多元线性回归模型

计量经济学-3多元线性回归模型
计量经济学-3多元线性 回归模型
2020/12/8
计量经济学-3多元线性回归模型
•第一节 概念和基本假定
•一、基本概念： • 设某经济变量Y 与P个解释变量：X1，X2，…，XP存在线性依
存关系。 • 1.总体回归模型：
•其中0为常数项， 1 ~ P 为解释变量X1 ~ XP 的系数，u为随机扰动项。 • 总体回归函数PRF给出的是给定解释变量X1 ~ XP 的值时，Y的期 望值：E ( Y | X1，X2，…，XP )。 • 假定有n组观测值，则可写成矩阵形式：
计量经济学-3多元线性回归模型
•2.样本回归模型的SRF
计量经济学-3多元线性回归模型
•二、基本假定： • 1、u零均值。所有的ui均值为0，E（ui）=0。 • 2、u同方差。Var（ui）=δ2，i=1，2，…，n
计量经济学-3多元线性回归模型
•
计量经济学-3多元线性回归模型
•
•第二节 参数的最小二乘估 计
•五、预测
•（一）点预测 •点预测的两种解释：
计量经济学-3多元线性回归模型
•（二）区间预测
计量经济学-3多元线性回归模型
计量经济学-3多元线性回归模型
计量经济学-3多元线性回归模型
计量经济学-3多元线性回归模型
计量经济学-3多元线性回归模型
•例5，在例1中，若X01=10，X02=10，求总体均值E（Y0|X0） 和总体个别值Y0的区间预测。
•
Yi=β0+β1Xi1+β2Xi2+ui
计量经济学-3多元线性回归模型
计量经济学-3多元线性回归模型
计量经济学-3多元线性回归模型
•三、最小二乘估计的性质
计量经济学-3多元线性回归模型

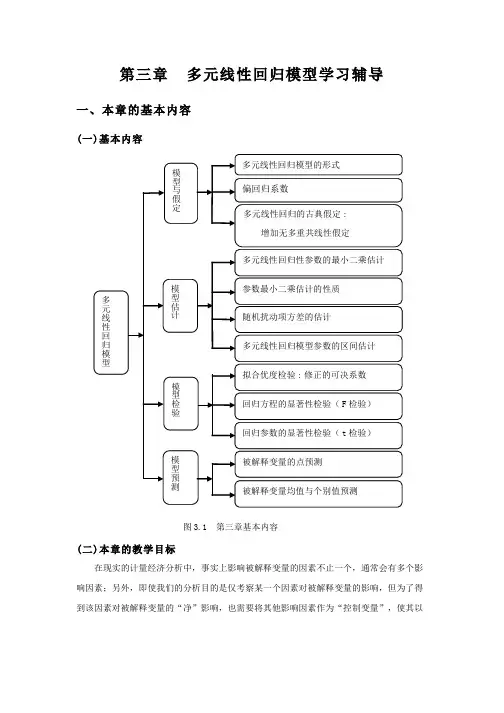
庞皓计量经济学第三章多元线性回归模型学习辅导

庞皓计量经济学第三章多元线性回归模型学习辅导

第三章 多元线性回归模型学习辅导一、本章的基本内容(一)基本内容图3.1 第三章基本内容(二)本章的教学目标在现实的计量经济分析中，事实上影响被解释变量的因素不止一个，通常会有多个影响因素；另外，即使我们的分析目的是仅考察某一个因素对被解释变量的影响，但为了得到该因素对被解释变量的“净”影响，也需要将其他影响因素作为“控制变量”，使其以显性形式出现在模型中，以提高模型估计精度。

因此，在对现实经济问题进行计量经济分析时，通常需要建立包含两个及两个以上解释变量的计量模型，此类模型称为多元回归模型。

多元回归模型是在简单回归模型理论基础上的扩展，其建模的理论基础、基本思路、模型估计等与一元回归模型基本一致，只是因解释变量增多，从而带来一些新的内容，比如模型整体显著性检验（F 检验）、修正的可决系数（2R ）以及解释变量之间多重共线性等问题。

本章的教学目标是：深刻理解建立多元回归模型的目的；掌握多元线性回归模型估计、检验的理论与方法；熟练掌握多元线性回归EViews 输出结果的解释。

二、重点与难点分析1.对多元线性回归模型参数意义的理解多元线性回归模型的参数与简单线性回归模型的参数有重要区别。

在多元线性回归模型中，解释变量对应的参数是偏回归系数，表达的是控制其他解释变量不变的条件下，该解释变量的单位变动对被解释变量平均值的“净”影响。

为了更深刻理解偏回归系数，可以两个解释变量的多元线性回归模型为例加以说明1。

例如，被解释变量Y 与解释变量2X 和3X 都有关，如果分别建立模型:多元线性回归: 12233i i i i Y X X u b b b =+++简单线性回归 : 1221i i i Y a a X u =++由于Y 与3X 有关，可以作回归:1332i i i Y b b X u =++，若用OLS 估计其参数，并计算残差213333ˆˆˆi i i i i e Y b b X y b x =--=-，这里的2i e 表示除去3i X 影响后的i Y 。

5、计量经济学【多元线性回归模型】

5、计量经济学【多元线性回归模型】

二、多元线性回归模型的参数估计
2、最小二乘估计量的性质 当 ˆ0, ˆ1, ˆ2, , ˆk 为表达式形式时，为随机变量， 这时最小二乘估计量 ˆ0, ˆ1, ˆ2, , ˆk 经过证明同样也 具有线性性、无偏性和最小方差性（有效性）。 也就是说，在模型满足那几条基本假定的前提 下，OLS估计量具有线性性、无偏性和最小方差性 （有效性）这样优良的性质， 即最小二乘估计量
用残差平方和 ei2 最小的准则： i
二、多元线性回归模型的参数估计
1、参数的普通最小二乘估计法（OLS） 即：
min ei2 min (Yi Yˆi )2 min Yi (ˆ0 ˆ1X1i ˆ2 X 2i ˆk X ki )2
同样的道理，根据微积分知识，要使上式最小，只 需求上式分别对 ˆj ( j 0,1, k) 的一阶偏导数，并令 一阶偏导数为 0，就可得到一个包含 k 1 个方程的正 规方程组，这个正规方程组中有 k 1个未知参数 ˆ0, ˆ1, ˆ2, , ˆk ；解这个正规方程组即可得到这 k 1 个参数 ˆ0, ˆ1, ˆ2, , ˆk 的表达式，即得到了参数的最小 二乘估计量；将样本数据代入到这些表达式中，即可 计算出参数的最小二乘估计值。
该样本回归模型与总体回归模型相对应，其中残差 ei Yi Yˆi 可看成是总体回归模型中随机误差项 i 的 估计值。
2、多元线性回归模型的几种形式： 上述几种形式的矩阵表达式： 将多元线性总体回归模型 (3.1) 式表示的 n 个随机方 程写成方程组的形式，有：
Y1 0 1 X11 2 X 21 .Y.2.........0.......1.X...1.2........2.X...2.2. Yn 0 1 X1n 2 X 2n
ˆ0, ˆ1, ˆ2, , ˆk 是总体参数真值的最佳线性无偏估计 量（ BLUE ）；即高斯—马尔可夫定理 (GaussMarkov theorem)。

计量经济学第三章 双变量线性回归模型

计量经济学第三章 双变量线性回归模型

xtYt
Y
xt
xt2
xt2
xt2
xt2
由于
xt (X t X ) X t X nX nX 0
从而
ˆ xtYt xt ( X t ut )
xt2
xt2
23
ˆ xtYt xt ( X t ut )
xt2
xt2
1 ( xt2
xt
14
残差平方和
我们的目标是使拟合出来的直线在某种意义上是最佳的， 直观地看，也就是要求估计直线尽可能地靠近各观测点，这意
味着应使残差总体上尽可能地小。要做到这一点，就必须用某
种方法将每个点相应的残差加在一起，使其达到最小。理想的 测度是残差平方和，即
et 2 (Yt Yˆt )2
15
最小二乘法
第三章 双变量线性回归模型 （简单线性回归模型）
（Simple Linear Regression Model）
2021/7/22
1
第一节 双变量线性回归模型的估计 第二节 最小二乘估计量的性质 第三节 拟合优度的测度 第四节 双变量回归中的区间估计和假
设检验 第五节 预测 第六节 有关最小二乘法的进一步讨论
9
（3）E(ut2)= 2, t=1,2,…,n 即各期扰动项的方差是一常数，也就是假定各扰
动项具有同方差性。
实际上该假设等同于：
Var( ut) = 2, t=1,2,…,n 这是因为：
Var(ut)=E{[ut-E(ut)]2}= E(ut2) ——根据假设（1）
10
（4） Xt为非随机量 即Xt的取值是确定的, 而不是随机的。 事实上，我们后面证明无偏性和时仅需要解释变量X与扰
是线性估计量。

计量经济学 詹姆斯斯托克 第3章 多元线性回归模型

计量经济学 詹姆斯斯托克 第3章 多元线性回归模型

i 2 i
10 21500 21500 53650000
1 X Y X1
1 X2
Y1 1 Y2 Yi 15674 X n X iYi 39468400 Yn
i i
638 1122 1155 1408 1595 1969 2078 2585 2530
ˆ 1
x y x
2 i
5769300 0.777 7425000
ˆ Y ˆ X 1567 0.777 2150 103 .172 0 0
因此，由该样本估计的回归方程（样本回归函数） 为：
i 1
n
2
ˆ ˆ X ˆ X ˆ X ))2 Q (Yi ( 0 1 1i 2 2i k ki
i 1
n
于是得到关于待估参数估计值的正规方程组：
ˆ ˆ X ˆ X ˆ X ) Y ( 0 1 1i 2 2i k ki i ˆ ˆ X ˆ X ˆ X ) X Y X ( 0 1 1i 2 2i k ki 1i i 1i ˆ ˆ X ˆ X ˆ X ) X Y X ( 0 1 1i 2i 2i k ki 2i i 2i ˆ ˆ ˆ ˆ ( 0 1 X 1i 2 X 2 i k X ki ) X ki Yi X ki
习惯上：把常数项看成为一个虚变量的系 数，该虚变量的样本观测值始终取1。这样： 模型中解释变量的数目为（k +1）。
Yi 0 1 X 1i 2 X 2 i k X ki i
也被称为 总体回归函数 的 随机表达形式 。它的 非随机表达式为:

计量经济学第三章第3节多元线性回归模型的显著性检验

计量经济学第三章第3节多元线性回归模型的显著性检验
2
当增加一个对被解释变量有较大影响的解释变量时， 残差平方和减小的比n-k-1 减小的更显著，拟合优度 就增大，这时就可以考虑将该变量放进模型。 如果增加一个对被解释变量没有多大影响的解释变量， 残差平方和减小没有n-k-1减小的显著，拟合优度会减 小，其说明模型中不应该引入这个不重要的解释变量， 可以将其剔除。
在对话框中输入：
y c x y(-1)
y c x y(-1) y(-2)
字母之间用空格分隔。 注：滞后变量不需重新形成新的时间序列，软件 自动运算实现，k期滞后变量，用y(-k)表示。
• 使用k期滞后变量，数据将损失k个样本观察值， 例如：
序号 2000 2001 2002 2003 2004 2005 2006 2007 2008 y 3 4 5 6 7 8 9 10 11 Y(-1) Y(-2) Y(-3)
2
2
2
*赤池信息准则和施瓦茨准则
• 为了比较所含解释变量个数不同的多元回归模型的 拟合优度，常用的标准还有: 赤池信息准则（Akaike information criterion, AIC） e e 2( k 1) AIC ln n n 施瓦茨准则（Schwarz criterion，SC）
一元、二元模型的系数均大于0，符合经济意义，三元模型 系数的符号与经济意义不符。 用一元回归模型的预测值是1758.7，二元回归模型的预测值 是1767.4，2001年的实际值是1782.2。一元、二元模型预测 的绝对误差分别是23.5、14.8。
3) 三个模型的拟合优度与残差
二元：R2 =0.9954，E2 ei2 13405 三元：R2 =0.9957，E3 ei2 9707
746.5 788.3

《计量经济学》第三章-多元线性回归模型(1)

《计量经济学》第三章-多元线性回归模型(1)

两边乘 X 有： X Y = X Xβˆ + X e
因为 Xe = 0 ，则正规方程为：
X Xβˆ = X Y
22
OLS估计式
由正规方程 多元回归中 二元回归中
X Xβˆ = X Y ( X X )kk 是满秩矩阵,其逆存在
βˆ = (X X)-1 X Y
ˆ1 Y - βˆ2 X2 - βˆ3X3
注意： x 和 y为 X,Y 的离差
23
二、OLS估计式的性质
OLS估计式
1.线性特征: βˆ = (X X)-1 X Y
βˆ 是 Y的线性函数，因 ( X X)-1 X 是非随机
或取固定值的矩阵
2.无偏特性: E(βˆk ) βk
24
3. 最小方差特性
在 βk 所有的线性无偏估计中，OLS估计 βˆk具有
E
u2
E
u2
0
un
E
un
0
假设２＆３：
Var(U ) E(U EU)(U EU) E(UU )
E(u1u1) E(u1u2 ) E(u1un ) 2 0 0
E
(u2u1
)
E(u2u2 )
E
(u2un
)
0
2
0
E
(unu1
)
E(unu2 )
E(unun )
求偏导,令其为0:
( ei2 )
ˆ j
0
20
即
-2 Yi - (ˆ1 ˆ2 X2i ˆ3X3i ... ˆki Xki ) 0
-2 X2i Yi - (ˆ1 ˆ2X2i ˆ3X3i ... ˆki Xki ) 0
ei 0 X2iei 0

计量经济学----几种常用的回归模型

计量经济学----几种常用的回归模型

• P175图6.10
几种常用的回归模型计量经济学回归模型计量经济学常用模型常用回归模型常用的回归模型计量经济学回归分析计量经济学线性回归计量经济学回归计量经济学逐步回归法计量经济学非线性回归
几种常用的回归模型
1. 对数线性模型 2. 半对数模型 3. 倒数模型 4. 对数倒数模型
1. 对数线性模型（不变弹性模型）
2的含义？
• 其测度了Y的瞬时增长率，即Y随着时间t变化的变 化率。 • 例如，Y为个人的年消费支出，t为年度，那么斜 率系数为个人消费支出的年增长率。
证明：
d(ln Y ) dY Y dY dt 2 dt dt Y
• 注意根据斜率系数的估计值也可以求出复 合增长率r的值。
线性到对数模型
回归子的相对改变量 2 回归元的绝对改变量
• 半对数模型的斜率系数度量了解释变量一个单位 的绝对变化，对应的因变量的相对变化量。 • P166例6.4
对数到线性模型（解释变量对数形式）
Yi 1 2 ln X i i
dY 2 d（lnX ) dX X
dY
2的含义？
证明：
d(ln Y ) dY Y 2 d(ln X ) dX X
适用性？
• 画出lnYi对lnXi的散点图，看是否近似为一 条直线，若是，则考虑此模型。 • P165例6.3
例：柯布--道格拉斯生产函数（P210）
Y AK L e


i
ln Y ln A ln K ln L i ln Y 0 lnK lnL i
• 其测度了X变化1%时Y的绝对变化量，当X变化1% 时，Y绝对变化为0.01 2
3. 倒数模型

计量经济学多元线性回归模型及参数估计

计量经济学多元线性回归模型及参数估计

-973 1314090 1822500 947508
-929 975870 1102500 863784
-445 334050 562500 198381
-412 185580 202500 170074
-159 23910 22500 25408
28 4140 22500
762
402 180720 202500 161283
2.多元线性回归模型的基本假定（矩阵形式）
V
ar
Cov( N
)
E
N
E(N
)N
E(
N
)
E(
NN
)
1
E
n2 1
2
12
n
E
2 1
n1
12 22
n2
1n
2n
n2
2
0
0
0
2
0
2
I
0
0
2
2.多元线性回归模型的基本假定（矩阵形式）
E(X
N )
E
1 X 11
ei 0 X i1ei 0 X i2ei 0
X ik ei 0
(*) (*)或（**）是多 元线性回归模型正
(**) 规方程组的另一种 写法。
离差形式的样本回归方程
由于
Yˆi ˆ0 ˆ1Xi1 ˆ2 Xi2 ˆk Xik
[Yi (ˆ0 ˆ1Xi1 ˆ2 Xi2 ˆk Xik )] 0
????eemm??所以有???eem??mnnee???ee?????????????????????????????????????????????nnnnnnnnmmmmmmmmme??????????????2121222211121121????????????????????????????????????????nnnnnnnnnnmmmmmmmmme?????????????????21221122221121221111因为xxxxim?????1为对称等幂矩阵即mm??mmmm???2????????nnnnnnnnnnmmmmmmmmme?????????????????????????????22112222211211221111??nnnnnmmmememem??????????22112222222111?????1212122??????????????kntrtrtrmtr????????xxxxixxxxi其中符号tr表示矩阵的迹其定义为矩阵主对角线元素的和

计量经济学第三章

计量经济学第三章
第三章 多元线性回归模型
多元线性回归模型及其古典假设 参数估计 最小二乘估计量的统计特性 统计显著性检验 解释变量的选择 中心化和标准化回归方程 利用多元线性回归方程进行预测
山东经济学院统计与数学学院计量经济教研室
第一节 多元线性回归模型 及其古典假设
一、多元线性回归模型的一般形式 二、多元线性回归模型的基本假定
山东经济学院统计与数学学院计量经济教研室
一、多元线性回归模型的一般形式
如果被解释变量（因变量）y与k个解释变量（ 自变量）x1, x2, … , xk 之间有线性相关关系，那么 他们之间的多元线性总体回归模型可以表示为：
y 0 1x1 2 x2 k xk u
(3.1)

(
k
1)1
en

n1
对样本回归模型的系统分量的系数进行估计可得样本回归
方程：
yˆi ˆ0 ˆ1x1i ˆ2x2i ˆk xki
yˆ i
其中， 是y的系统分量，即由自变量决定的理论值， ˆ0,ˆ1,ˆ2,,ˆk
分别是0 ,1 ,…,k的无偏估计量。
方程表示：各变量x值固定时y的平均响应。
j也被称为偏回归系数，表示在其他解释变量
保持不变的情况下，xj每变化1个单位时，y的均 值E(y)的变化;
或者说j给出了xj的单位变化对y均值的“直
接”或“净”（不含其他变量）影响。
山东经济学院统计与数学学院计量经济教研室
总体回归模型n个随机方程的为：
y1 0 1x11 2 x21 k xk1 u1 y2 01x12 2x22 kxk2 u2 yn 0 1x1n 2 x2n k xkn un

计量经济学(第五版)教学课件3

计量经济学(第五版)教学课件3
• 在采用OLS进行参数估计时，不需要正态性假 设。在利用参数估计量进行统计推断时，需要 假设随机项的概率分布。
• 一般假设随机项服从正态分布。
• 正态性假设。The μ’s follow the normal distribution.
i ~ N(0, 2) i ~ NID(0, 2)
在矩阵视角下，上述假设可写成矩阵形式
第三章 经典单方程计量经济学模型：多 元线性回归模型
§3.1 多元线性回归模型
一、多元线性回归模型 二、多元线性回归模型的基本假设
一、多元线性回归模型
1、总体回归模型
• 总体回归模型：总体回归函数的随机表达形式 Yi 0 1 X i1 2 X i2 k X ik i i=1,2…,n
coefficients)，表示在其他解释变量保持不变 的情况下，Xj每变化1个单位时，Y的均值 E(Y)的变化。
或者说j给出了Xj的单位变化对Y均值的
“直接”或“净”（不含其他变量）影响。
3、总体回归模型的矩阵表示
Y Xβ μ
1 X 11
X
1
X 12
1 X 1n
X 21 X 22
X 2n
Yi 0 1 X 1i 2 X 2i k X ki i
注意：“linear in the parameters”的含义是什 么？
2、关于解释变量的假设
• 与随机项不相关假设。The covariances between Xij and μi are zero.
2、关于解释变量的假设
X k1
X
k
2
X
kn
n(k 1)
Y1
Y
Y2
Yn
n1
0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

根据矩阵的概念, 标准的回归可以写为：
y Xβ u
其中: y 是因变量观测值的 T 维向量，X 是解释变量观测值的 T k 维矩阵，T 是观测值个数，k 是解释变量个数， 是 k 维 系数向量，u 是 T 维扰动项向量。 10
§3.2.1
列表法
说明线性方程的最简单的方法是列出方程中要使用的变 量列表。首先是因变量或表达式名，然后是自变量列表。例 如，要说明一个线性消费函数，用一个常数 c 和收入 inc 对 消费 cs 作回归，在方程说明对话框上部输入： cs c inc 注意回归变量列表中的序列 c。这是EViews 用来说明回 归中的常数而建立的序列。 EViews在回归中不会自动包括一 个常数，因此必须明确列出作为回归变量的常数。内部序列 c 不出现在工作文档中，除了说明方程外不能使用它。 在上例中，常数存储于c(1)，inc的系数存储于c(2)，即 回归方程形式为： cs = c(1)+c(2)*inc。
程，并选择估计方法。
3
§3.2 在EViews中对方程进行说明
当创建一个方程对象时，会出现如下对话框：
在这个对话框中需要说明三件事：方程说明，估计方法，估 计使用的样本。在最上面的编辑框中，可以说明方程：因变量 （左边）和自变量（右边）以及函数形式。 有两种说明方程的基本方法：列表法和公式法。列表法简单 但是只能用于不严格的线性说明；公式法更为一般，可用于说明 4 非线性模型或带有参数约束的模型。
标准的单方程回归用最小二乘估计。其他的方法在以后的 章节中介绍。采用 OLS， TSLS ， GMM，和ARCH方法估计的 方程可以用一个公式说明。非线性方程不允许使用 binary ， ordered，censored，count模型，或带有ARMA项的方程。
9
§3.4
方程输出
在方程说明对话框中单击OK钮后，EViews显示估计结果：
6
§3.2.2
公式法说明方程
当列表方法满足不了要求时，可以用公式来说明方程。
许多估计方法（但不是所有的方法）允许使用公式来说明方
程。 EViews 中的公式是一个包括回归变量和系数的数学表 达式。要用公式说明一个方程，只需在对话框中变量列表处 输入表达式即可。 EViews 会在方程中添加一个随机附加扰
量图标 的对象会列在工作文档目录中，在方程说明中就
可以使用这个系数向量。例如，假设创造了系数向量 a 和 beta，各有一行。则可以用新的系数向量代替 c ： log(cs)=a(1)+ beta(1)* log(cs(-1))
8
§3.3
在EViews中估计方程
说明方程后,现在需要选择估计方法。单击Method：进入对 话框，会看到下拉菜单中的估计方法列表：
第三章 基本回归模型
经济计量研究始于经济学中的理论假设，根据经济理 论设定变量间的一组关系，如消费理论、生产理论和各种 宏观经济理论，对理论设定的关系进行定量刻画，如消费 函数中的边际消费倾向、生产函数中的各种弹性等进行实 证研究。单方程回归是最丰富多彩和广泛使用的统计技术 之一。本章介绍EViews中基本回归技术的使用，说明并估 计一个回归模型，进行简单的特征分析并在深入的分析中 使用估计结果。随后的章节讨论了检验和预测，以及更高 级，专业的技术，如加权最小二乘法、二阶段最小二乘法 (TSLS)、非线性最小二乘法、ARIMA/ARIMAX模型、 GMM（广义矩估计）、GARCH模型和定性的有限因变量 模型。这些技术和模型都建立在本章介绍的基本思想的基 础之上。
5
在统计操作中会用到滞后序列，可以使用与滞后序列相同的 名字来产生一个新序列，把滞后值放在序列名后的括号中。 cs c cs(-1) inc 相当的回归方程形式为： cs = c(1)+ c(2) cs(-1)+c(3) inc。 通过在滞后中使用关键词 to 可以包括一个连续范围的滞后 序列。例如：
1
对于本章及随后章节所讨论的技术，可以使用下列的经 济计量学教科书作为参考。下面列出了标准教科书(逐渐变难)： (1) Pindyck，Rubinfeld (1991), Econometric Models and Economic Forecasts, 《经济计量模型和经济预测》，第三版。 (2) Johnston 和 DiNardo (1997)，Economtric Methods, 《经济计量方法》，第四版。 (3) Greene (1997)，Economtric Analysis, 《经济计量分 析》，第三版。 (4) Davidson 和 MacKinon (1993) ， Estimation and Inference in Econometrics , 《经济计量学中的估计和推断》。 在适当的地方，对于特定的专题, 我们也会提供专门的参数。
7
用公式说明方程的好处是可以使用不同的系数向量。
要创建新的系数向量，选择Object/New Object… 并从主 菜单中选择Matrix-Vector-Coef , 为系数向量输入一个名字。 然 后 ， 选 择 OK 。 在 New Matrix 对 话 框 中 ， 选 择 Coefficient Vector 并说明向量中应有多少行。带有系数向
2
§3.1 创建方程对象
EViews中的单方程回归估计是用方程对象来完成 的。为了创建一个方程对象: 从主菜单选择Object/New
Object/Equation 或 Quick/Estimation Equation …，或
者在命令窗口中输入关键词equation。 在随后出现的方程说明对话框中说明要建立的方
cs c cs(-1 to -4) inc 这里cs关于常数，cs(-1)，cs(-2)，cs(-3)，cs(-4)，和inc的回归。 在变量列表中也可以包括自动序列。例如： log(cs) c log(cs(-1)) log((inc+inc(-1))/2) 相当的回归方程形式为： log(cs) = c(1)+c(2) log(cs(-1))+c(3) log((inc+inc(-1))/2)