当前位置：文档之家 › 第三章 多元线性回归模型

第三章 多元线性回归模型

  • 格式：doc
  • 大小：32.50 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

第三章 多元线性回归模型

第三章 多元线性回归模型

即
Y Xb U
X 称为数据矩阵或设计矩阵。
6
二、古典假定
假定1：零均值假定 E(ui ) 0 (i 1,2,...,n)
1 E ( 1 ) E ( ) 2 2 E (μ) E 0 n E ( n )
写成矩阵形式：
Y1 1 X 21 Y 1 X 22 2 Yn 1 X 2 n X 31 X k 1 b 1 u1 X 32 X k 2 b 2 u 2 X 3 n X kn b k un
或
ei 1 X 21 X e 1 X 22 2i i X ki ei 1 X 2 n X 31 X k 1 e1 X 32 X k 2 e2 X e 0 X 3 n X kn en
9
当总体观测值难于得到时，回归系数向 量 b 是未知的，这时可以由样本观测值进行 估计，可表示为
ˆ ˆ Xb Y
但实际观测值与计算值有偏差，记为：
ˆ e Y Y
于是
ˆ e Y Xb
称为多元样本回归函数。
10
ˆ b 1 ˆ b2 ˆ b ˆ b k
同理
ˆ x x b ˆ x 2 x3 i yi b 2 2i 3i 3 3i
x2 i yi x x3 i yi x2 i x3 i ˆ b2 2 2 2 x2 x ( x x ) i 3i 2i 3i
2 3i
x3 i yi x x2 i yi x2 i x3 i ˆ b3 2 2 2 x2 x ( x x ) i 3i 2i 3i

第三章多元线性回归模型(计量经济学,南京审计学院)

第三章多元线性回归模型(计量经济学,南京审计学院)

Yˆ 116.7 0.112X 0.739P
R2 0.99
(9.6) (0.003) (0.114)
Y和X的计量单位为10亿美元 (按1972不变价格计算).
P
食品价格平减指数 总消费支出价格平减指数
100，（1972
100）
3
多元线性回归模型中斜率系数的含义
上例中斜率系数的含义说明如下： 价格不变的情况下，个人可支配收入每上升10
c (X X )1 X D
从而将 的任意线性无偏估计量 * 与OLS估计量 ˆ 联系
起来。
28
cX I
由
可推出：
(X X )1 X X DX I
即 I DX I
因而有 D X 0
cc (X X )1 X D (X X )1 X D ( X X )1 X D X ( X X )1 D
第三章 多元线性回归模型
简单线性回归模型的推广
1
第一节 多元线性回归模型的概念
在许多实际问题中，我们所研究的因变量的变动 可能不仅与一个解释变量有关。因此，有必要考虑线 性模型的更一般形式，即多元线性回归模型：
Yt β0 β1X1t β2 X 2t ... βk X kt ut t=1,2,…,n
Yt
ˆ0
βˆ 1
X
1t
... βˆ K X Kt
2
为最小，则应有：
S
S
S
ˆ0 0, ˆ1 0, ..., ˆ K 0
我们得到如下K+1个方程（即正规方程）：
13
β0 n
β1 X1t ...... β K X Kt Yt
β 0 X 1t β1 X 1t 2 ...... β K X 1t X Kt X 1tYt

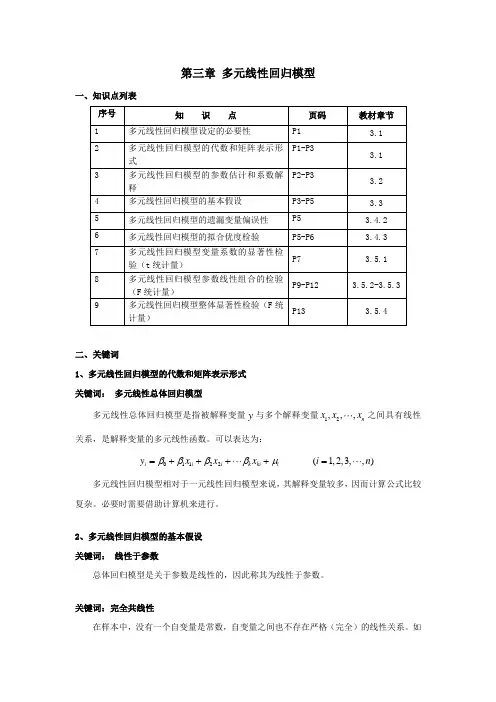
第三章 多元线性回归模型 知识点

第三章 多元线性回归模型 知识点

第三章 多元线性回归模型一、知识点列表二、关键词1、多元线性回归模型的代数和矩阵表示形式 关键词： 多元线性总体回归模型多元线性总体回归模型是指被解释变量y 与多个解释变量12,,,n x x x 之间具有线性关系，是解释变量的多元线性函数。

可以表达为：01122(1,2,3,,)i i i k ki iy x x x i n ββββμ=++++=多元线性回归模型相对于一元线性回归模型来说，其解释变量较多，因而计算公式比较复杂。

必要时需要借助计算机来进行。

2、多元线性回归模型的基本假设 关键词： 线性于参数总体回归模型是关于参数是线性的，因此称其为线性于参数。

关键词：完全共线性在样本中，没有一个自变量是常数，自变量之间也不存在严格（完全）的线性关系。

如果方程中有一个自变量是其他自变量的线性组合，那么我们说这个模型遇到了完全共线性问题。

关键词：零条件数学期望给定解释变量的任何值，误差的期望值为零，即：12(|,,,)0n E u x x x =。

关键词：内生解释变量和外生解释变量如果解释变量满足零条件数学期望，则称该自编为内生解释变量；反之，则为外生解释变量。

关键词：同方差对于解释变量的所有观测值，随机误差项有相同的方差，即：22()(),(1,2,3,,)i i Var u E u i n δ===关键词：无序列相关性随机误差项两两不相关。

即(,)(,)0,(,,1,2,3,,)i i i i Cov u u E u u i j i j n ==≠=关键词：最优线性无偏估计量满足以下假设条件的OLS 估计量称为最优线性无偏估计量：（1）线性与参数；（2）X 固定；（3）X 有变异；（4）不存在完全共线性；（5）零条件数学期望；（6）同方差；（7）无序列相关性。

关键词：经典正态线性回归模型如果回归模型的OLS 估计量为最优线性无偏估计量，并且随机误差项u 服从均值为零，方差为2δ的正态分布，则称该线性回归模型为经典正态线性回归模型。

第3章多元线性回归

第3章多元线性回归



E (β XX1Xε-β)(β XX1Xε-β)
E XX1Xεε XXX1 XX1XE(εε )XXX1
XX1XE( 2In )XXX1 2 XX1
3.3 参数估计量的性质
i 1
i 1
ˆ
2

n

1 p
1
SSE

n

1 p
(ee) 1
n
1 p
1
n i 1
ei2
是σ2的无偏估计
3.2 回归参数的估计
三 、回归参数的最大似然估计
y～N(Xβ ,σ 2In)
似然函数为
L
(2 )n
2
2
n
2
exp(
1
2
2
(y - Xβ)(y - Xβ))
βˆ (XX)-1 Xy
3.2 回归参数的估计
二、回归值与残差
称 yˆi ˆ0 ˆ1xi1 ˆ2xi2 ˆp xip 为回归值
yˆ Xβˆ X(XX)-1 Xy H X(X X)-1X
称为帽子矩阵，其主对角线元素记为hii ，则
3.2 回归参数的估计
二、回归值与残差
n
tr(H ) hii p 1 i 1
此式的证明只需根据迹的性质tr(AB)=tr(BA),因而
tr(H) tr(X(XX)-1X) tr(XX(XX)-1) tr(Ip1) p 1
3.2 回归参数的估计
二、回归值与残差
e y yˆ y Hy (I- H)y
x 2
Lxx
x 2
Lxx

2

L xx

第三章(1) 多元线性回归模型课件

第三章(1) 多元线性回归模型课件

分离差的大小
解释的那部分离差的大小。也
称剩余平方和。
第三章 多元线性回归模型
§ 3-3 多元线性回归模型的统计检验 一、 拟合优度检验 检验模型对样本观测值的拟合程度。用在总离差分解 基础上确定的可决系数R2 (调整的可决系数 ) 度量。 1、总离差平方和的分解
总离差平方和TSS 回归平方和ESS
3、随机误差项在不同 样本点之间是独立的，
Cov( i,
不存在序列相关
因为 i与 j相互独立，有：
j)=0 i≠j
无自相关假定表明：产生 误差(干扰)的因素是完 全随机的，此次干扰与彼 次干扰互不相关，互相独 立。由此应变量Yi的序列 值之间也互不相关。
第三章 多元线性回归模型
§ 3-1 多元线性回归模型及其基本假定
3、有效性(最小方差性)：
指在所有线性、无偏估计量中， OLS参数估计量的 方差最小。
4、 服从正态分布，即：
其中，
， G2是随机误差项的方差，
Cjj是矩阵(X’X)-1 中第j行第j列位置上的元素。
第三章 多元线性回归模型
§ 3-2 多元线性回归模型的参数估计
一、 参数的最小二乘估计
二、 OLS估计量的统计性质及其分布
三、随机误差项方差Q2的估 计
参数估计的另一项任务是： 求随机误差项 i 的分布参数
称作回归标准差 (standard error of regression)， 常作为对所估计回归线的拟
合优度的简单度量。
i~N(0, Q2)
随机误差项 i 的 方差的估计量为：
可以
证明：
说明 是QS 的无偏估计量。
t-Statistic 6.411848 22.00035 4.187969

5、计量经济学【多元线性回归模型】

5、计量经济学【多元线性回归模型】

二、多元线性回归模型的参数估计
2、最小二乘估计量的性质 当 ˆ0, ˆ1, ˆ2, , ˆk 为表达式形式时，为随机变量， 这时最小二乘估计量 ˆ0, ˆ1, ˆ2, , ˆk 经过证明同样也 具有线性性、无偏性和最小方差性（有效性）。 也就是说，在模型满足那几条基本假定的前提 下，OLS估计量具有线性性、无偏性和最小方差性 （有效性）这样优良的性质， 即最小二乘估计量
用残差平方和 ei2 最小的准则： i
二、多元线性回归模型的参数估计
1、参数的普通最小二乘估计法（OLS） 即：
min ei2 min (Yi Yˆi )2 min Yi (ˆ0 ˆ1X1i ˆ2 X 2i ˆk X ki )2
同样的道理，根据微积分知识，要使上式最小，只 需求上式分别对 ˆj ( j 0,1, k) 的一阶偏导数，并令 一阶偏导数为 0，就可得到一个包含 k 1 个方程的正 规方程组，这个正规方程组中有 k 1个未知参数 ˆ0, ˆ1, ˆ2, , ˆk ；解这个正规方程组即可得到这 k 1 个参数 ˆ0, ˆ1, ˆ2, , ˆk 的表达式，即得到了参数的最小 二乘估计量；将样本数据代入到这些表达式中，即可 计算出参数的最小二乘估计值。
该样本回归模型与总体回归模型相对应，其中残差 ei Yi Yˆi 可看成是总体回归模型中随机误差项 i 的 估计值。
2、多元线性回归模型的几种形式： 上述几种形式的矩阵表达式： 将多元线性总体回归模型 (3.1) 式表示的 n 个随机方 程写成方程组的形式，有：
Y1 0 1 X11 2 X 21 .Y.2.........0.......1.X...1.2........2.X...2.2. Yn 0 1 X1n 2 X 2n
ˆ0, ˆ1, ˆ2, , ˆk 是总体参数真值的最佳线性无偏估计 量（ BLUE ）；即高斯—马尔可夫定理 (GaussMarkov theorem)。

第三章 多元线性回归模型

第三章 多元线性回归模型
R 2 = 1− RSS /( n − k − 1) TSS /( n − 1)
其中：n-k-1为残差平方和的自由度，n-1为总体平 方和的自由度。
检验) 三、方程的显著性检验(F检验 方程的显著性检验 检验
方程的显著性检验， 方程的显著性检验，旨在对模型中被解释变 量与解释变量之间的线性关系在总体上 在总体上是否显著 量与解释变量之间的线性关系在总体上是否显著 成立作出推断。 成立作出推断。 即检验模型
写成矩阵形式： 写成矩阵形式：
Y = Xb + µ
其中
Y1 Y2 Y = M Yn
1 1 X = M 1 X 11 X 12 M X 1n X 21 X 22 M X 2n L L L X k1 X k2 M X kn n × ( k +1 )
回归系数的显著性检验（ 检验 检验） 第五节 回归系数的显著性检验（t检验）
方程的总体线性 总体线性关系显著≠每个解释变量 总体线性 ≠每个解释变量对被 解释变量的影响都是显著的 因此，必须对每个解释变量进行显著性检验， 以决定是否作为解释变量被保留在模型中。 检验完成的。 这一检验是由对变量的 t 检验完成的。
或
1 x ′x → Q n
其中：Q为一非奇异固定矩阵，矩阵x是由各解释变量 的离差为元素组成的n×k阶矩阵
x11 L x k1 x= M L M x 1n L x kn
假设6，回归模型的设定是正确的。
第二节 参数的最小二乘估计
一、回归参数的最小二乘估计 二、随机项µ的方差的估计量 随机项 的方差的估计量
( )
( )
( )
= E ( X ′X
)

第三章多元线性回归模型

第三章多元线性回归模型

命令或特殊函数命令得到。特殊函数命令：在工作文件窗
口，使用GSexi nr命S令y 生成，x如i 序列y的标准为
），
@ stdev( y)
26
案例2 我国房地产行业资本结构分析
资本结构是指企业各种资本的价值构成及其 比例关系。合理安排资本结构有利于增加公司的市场价 值。本案例运用多元回归分析方法研究了我国房地产上 市公司的资本结构，证实了成长能力、营运效率、内部 流动率、盈利能力等因素对房地产上市公司的资本结构 （以资产负债率为衡量指标）有显著影响。
28
表3.2资本结构的影响因素对应指标和变量
影响因素 对应指标
变量
成长能力 总资产增长率
x1
股东权益周转率 x2
营运效率 总资产周转率
x3
内部流动率 流动比率
x4
盈利能力 销售净利率
x5
29
根据以上的叙述，拟建立如下截面多元线 性回归模型：
yi 0 1x1i 2 x2i 3x3i 4 x4i 5x5i ui


Q
k
2
( yt 0 1x1t 2 x2t
k xkt ) =0 k xkt )x1t =0
k xkt )xkt =0
化简整理得多元线性回归正规方程组：
13


yt = n0 +1 x1t yt 0 x1t 1 x2t yt 0 x2t 1
进一步改写为：
1 1

x11
x12

x21
x22

xk1 xk2
1 1 x11 x21
x1n

三章多元线回归模型

三章多元线回归模型

多元模型的矩阵表达式
Y X
1
1
11
Y X
21
12
Y X
n
1
1n
X21 X22
X2n
X X X bbbb uuu kkk12n
k102
1 2 n
YXB U
矩阵形式
Y XB U
Y 1
Y
Y 2
Y n
b 0
B
b b
1 2
b k
X 1
11
X X
（4）应变量估计值 Y i 与残差 ei不相关；
（5）解释变量
X
与残差
i
ei不相关
2.3 随机扰动项方差的估计
2
扰动项的方 2估 差计：
ei2
nk
其中n为样本容量 k为， 待估参数个数。
（比较：一元情 2 形e： i2，待估参数 2个有 ）
n2
注解：k与k+1
凡是按解释变量的个数为k的，那么共有k+1 个参数要估计。而按参数个数为k的，则实 际有k-1个解释变量。总之两者相差1而已！ 要小心所用的k是什么意思！
E(NN)(X X )1 X X ( X X )1
2 ( X X )1
2.2 OLS回归线的性质
完全同一元情形：
（1）回归线过样本均值
Y 1 2 X 2i 3 X 3i ... k X ki
(2)估计值 Y i 的均值等于实际观测值 Yi的均值
(3)剩余项（残差） ei的均值为 0
1
12
X 1
1n
X 21 X 22
X 2n
u 1
U
u2
u n

《计量经济学》第三章 多元线性回归模型

《计量经济学》第三章 多元线性回归模型
总体回归函数也可表示为:
Yi 1 2 X 2i 3 X 3i ... k X ki ui
7
多元样本回归函数
Y 的样本条件均值表示为多个解释变量的函数
ˆ ˆ ˆ ˆ ˆ Yi 1 2 X 2i 3 X3i ... k X ki
或
ˆ ˆ ˆ ˆ Yi 1 2 X 2i 3 X3i ... k X ki ei
22
ˆ ˆ 因 2 是未知的，可用 2代替 2 去估计参数 β 的标
准误差:
ˆ ● 当为大样本时，用估计的参数标准误差对 β 作标 准化变换，所得Z统计量仍可视为服从正态分布 ˆ ●当为小样本时，用估计的参数标准误差对 β 作标
准化变换，所得的t统计量服从t分布： ˆ βk - βk t ~ t (n - k ) ^ ˆ SE( βk )
i i
i
e e 0 4.残差 ei 与 X 和
3.
i
e X
i
3i
ei X 2i 0
2i
X 3i 都不相关，即
ˆ 5.残差 ei 与 Yi 不相关，即
e Yˆ 0
i i
18
二、OLS估计式的性质－统计性质
OLS估计式（用矩阵表式） 1.线性特征:
ˆ = (X X)-1 X Y β
2 i
ˆ ei2 (Yi - Yi )2
ˆ X X ... X )]2 ˆ min e [Yi -(1 ˆ2 2i ˆ3 3i k ki
求偏导,令其为0:
( ei2 ) 0 ˆ
j
13
即 ˆ ˆ ˆ ˆ -2 Yi - (1 2 X 2i 3 X 3i ... ki X ki ) 0

第03章-多元线性回归模型

第03章-多元线性回归模型
2 u2
M u u2 1
K u uT 1 K u uT 1 O M 2 K uT
2 E(u1 ) E(u2u1) = M E(uT u1)
E(u1u2 ) K E(u1uT ) σ 2 0 K 0 2 E(u2 ) K E(u2uT ) 0 σ 2 K 0 = σ 2I = M M M M O M 0 K σ2 0 2 E(uT u2 ) K E(uT )
因此： 这个模型相应的矩阵表示形式 因此： 这个模型相应的矩阵表示形式为：Y = Xβ + U 矩阵表示形式为
y1 y2 Y= M yT (T ×1)
1 1 X= L 1 x11 x21 L xT 1 x12 x22 L xT 2 x13 L x1k x23 L x2 k L L L xT 3 L xTk T ×( k +1)
§3.2 最小二乘法
一、参数的最小二乘估计…… 参数的最小二乘估计 二、随机误差项方差σ2的估计量 随机误差项方差σ 的估计量……
一、参数的最小二乘估计
– 根据最小二乘准则： 根据最小二乘准则：
ˆ ˆ ˆ ˆ Q ( β 0 , β 1 , β 2 , … , β k）
=
∑
=
T
t =1
et =
2
二、随机误差项方差σ 二、随机误差项方差σ2的估计量
首先，残差的表示形式： 首先，残差的表示形式：
) ˆ e = Y − Y = Y − Xβ = ( Xβ + u) − X [( X' X ) −1 X' Y ] = ( Xβ + u) − X [( X' X )−1 X' ( Xβ + u)]

第三章多元线性回归模型

第三章多元线性回归模型

第三章 多元线性回归模型一、名词解释1、多元线性回归模型：在现实经济活动中往往存在一个变量受到其他多个变量影响的现象，表现在线性回归模型中有多个解释变量，这样的模型被称做多元线性回归模型，多元是指多个解释变量2、调整的可决系数2R ：又叫调整的决定系数，是一个用于描述多个解释变量对被解释变量的联合影响程度的统计量，克服了2R 随解释变量的增加而增大的缺陷，与2R 的关系为2211(1)1n R R n k -=----。

3、偏回归系数：在多元回归模型中，每一个解释变量前的参数即为偏回归系数，它测度了当其他解释变量保持不变时，该变量增加1单位对被解释变量带来的平均影响程度。

4、正规方程组：采用OLS 方法估计线性回归模型时，对残差平方和关于各参数求偏导，并令偏导数为0后得到的方程组，其矩阵形式为ˆX X X Y β''=。

5、方程显著性检验：是针对所有解释变量对被解释变量的联合影响是否显著所作的检验，旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出判断。

二、单项选择题1、C ：F 统计量的意义2、A ：F 统计量的定义3、B ：随机误差项方差的估计值1ˆ22--=∑k n e iσ4、A ：书上P92和P93公式5、C ：A 参看导论部分内容；B 在判断多重共线等问题的时候，很有必要；D 在相同解释变量情况下可以衡量6、C ：书上P99，比较F 统计量和可决系数的公式即可7、A ：书P818、D ：A 截距项可以不管它；B 不考虑beta0；C 相关关系与因果关系的辨析 9、B ：注意！只是在服从基本假设的前提下，统计量才服从相应的分布10、D ：AB 不能简单通过可决系数判断模型好坏，还要考虑样本量、异方差等问题；三、多项选择题1、ACDE ：概念性2、BD ：概念性3、BCD ：总体显著，则至少一个参数不为04、BC ：参考可决系数和F 统计量的公式5、AD ：考虑极端情况，ESS=0，可发现CE 错四、判断题、 1、√2、√3、×4、×：调整的可决系数5、√五、简答题 1、 答：多元线性回归模型与一元线性回归模型的区别表现在如下几个方面：一是解释变量的个数不同；二是模型的经典假设不同，多元线性回归模型比一元线性回归模型多了个“解释变量之间不存在线性相关关系”的假定；三是多元线性回归模型的参数估计式的表达更为复杂。

第三章-多元线性回归模型ppt课件

第三章-多元线性回归模型ppt课件

32
§3.5 最小二乘估计量的特征
上一章中谈到，经典一元线性回归模
型的OLS估计量满足线性、无偏及方差最
小性，即高斯——马尔可夫定理，对于经
典多元线性回归模型的普通最小二乘估计
量，这一性质仍然存在，换言之，对于满
足经典假设的多元线性回归模型，采用
OLS方法所得估计量 也满足线性、无偏
及方差最小性。 ppt精选版
ˆ 3
yi x3i
x
2 2i
x
2 2i
yi x2i
x2i x3i
x32i ( x2i x3i ) 2
ppt精选版
30
解方程时的系数行列式：
x22i
x2ix3i
x2ix3i
x32i
解 ˆ2 时的分子行列式：
yix2i
x2ix3i
yix3i
x32i
ppt精选版
31
第三章 第五节
ppt精选版
Y 01P2D P 3P I 2 U
ppt精选版
5
二、多元总体线性回归模型 总体模型： 1、分量式：
Y i 0 1 X 1 i 2 X 2 i k X k u ii
2、总量式
Y 01X 1 ppt精选版2X 2 kX k 6U
称 之 为 变 量 Y 关 于 变 量 X1, X2, …, Xk的k元总体线性回 归模型，Y称为被解释变量 ，X1, X2, …, Xk称为解释变 量，k 称为解释变量个数， U 称为随机扰动项，或随机 项，或扰动项。
一、多元总体线性回归模型的矩阵表示
YX βU Y1
Y
Y
2
Yn
1 X 21 X k1
X
1
X 22

计量经济学 詹姆斯斯托克 第3章 多元线性回归模型

计量经济学 詹姆斯斯托克 第3章 多元线性回归模型

i 2 i
10 21500 21500 53650000
1 X Y X1
1 X2
Y1 1 Y2 Yi 15674 X n X iYi 39468400 Yn
i i
638 1122 1155 1408 1595 1969 2078 2585 2530
ˆ 1
x y x
2 i
5769300 0.777 7425000
ˆ Y ˆ X 1567 0.777 2150 103 .172 0 0
因此，由该样本估计的回归方程（样本回归函数） 为：
i 1
n
2
ˆ ˆ X ˆ X ˆ X ))2 Q (Yi ( 0 1 1i 2 2i k ki
i 1
n
于是得到关于待估参数估计值的正规方程组：
ˆ ˆ X ˆ X ˆ X ) Y ( 0 1 1i 2 2i k ki i ˆ ˆ X ˆ X ˆ X ) X Y X ( 0 1 1i 2 2i k ki 1i i 1i ˆ ˆ X ˆ X ˆ X ) X Y X ( 0 1 1i 2i 2i k ki 2i i 2i ˆ ˆ ˆ ˆ ( 0 1 X 1i 2 X 2 i k X ki ) X ki Yi X ki
习惯上：把常数项看成为一个虚变量的系 数，该虚变量的样本观测值始终取1。这样： 模型中解释变量的数目为（k +1）。
Yi 0 1 X 1i 2 X 2 i k X ki i
也被称为 总体回归函数 的 随机表达形式 。它的 非随机表达式为:

第三章多元线性回归模型

第三章多元线性回归模型

( k + 1 )×1
1 2 μ= M n n ×1
用来估计总体回归函数的样本回归函数 ： 样本回归函数为： 样本回归函数
Yi = β 0 + β1 X1i + β 2 X 2i + L+ β ki X ki
样本观测值: 样本观测值:
Yi = β0 +β1X1i +β2 X2i +L+βkiXki +ei
b10、 β1的经济涵义、先验符号？
例1 “期望扩充”菲利普斯曲线
估计结果
原始菲利普斯曲线
yt = 6.127172+ 0.244934x1t se : 4.285283 0.630456 t : 1.429817 0.388502 p : 0.180552 0.705058 R2 = 0.013536 F = 0.150934 p( F ) = 0.705058
1i 2 i 2 1i
2 2i
对有k 对有k个解释变量的多元回归模型
, 对于随机抽取的n组观测值 (Yi , X ji ),i =1,2,L n, j = 0,1,2,Lk
如果样本函数 样本函数的参数估计值已经得到，则有： 样本函数
Yi = β 0 + β 1 X 1i + β 2 X 2i + L + β ki X Ki
n n
n
i=1,2…n
2
Q = ∑ei2 = ∑(Yi Yi )2 = ∑(Yi (β0 + β1X1i + β2 X2i +L+ βk Xki ))
i =1 i=1
i=1
根据最小二乘原理 最小二乘原理， 最小二乘原理 参数估计值应该是右列 方程组的解

第三章 多元回归模型

第三章 多元回归模型
其计算公式如下:
r0i,12i1i1k
r r r 0i,12i1i1k 1 0k ,12k 1 ik ,12i1i1k 1
1 r02k,12k1
1
r2
ik ,12i1i1k
1
问题：在多元回归中 r12(i1)(i1)k ,0 是越大越好，
还是越小越好？
17
模型显著性检验（F检验）: F统计量
核心思想：残差平方和最小准则
min ei2 min yi yˆi 2
min yi ˆ0 ˆ1x1i ˆ2x2i ˆk xki 2
求解原理
ei2
ˆ j
0
结论
j 0,1,2,, k
ˆ X ' X 1 X 'Y
8
例子
经过研究，发现家庭书刊消费水平受家庭 收入及户主教育年数的影响。现对某地区 的家庭进行抽样调查，得到的样本数据如 表所示，其中 y 表示家庭书刊消费水平
其中，n k 1为 ei2 的自由度，n 1 为 yi y2
的自由度
引入修正的样本决定系数R 2的作用：
用自由度调整后，可以消除拟合优度评价中解释变量多 少对决定系数计算的影响
对于包含的解释变量个数不同的模型，可以用调整后的 决定系数直接比较它们的拟合优度的高低，但不能用原 来未调整的决定系数来比较
零阶偏相关系数、一阶偏相关系数、k 1 阶偏相关系数
r01 为零阶偏相关系数、 r02,1 称为一阶偏相关系数、 r01,23 称
为二阶偏相关系数、r01,234 称为三阶偏相关系数，依此类推
16
偏相关系数：一般公式
一般地，在研究多个变量的偏相关系数时，因变量 y
与解释变量 xi i 1,2,, k 的k 1 阶偏相关系数时，

计量经济学课件：第三章 多元线性回归模型

计量经济学课件：第三章 多元线性回归模型

第三章 多元线性回归模型第一节 多元线性回归模型及基本假定问题：只有一个解释变量的线性回归模型能否满足分析经济问题的需要？简单线性回归模型的主要缺陷是：把被解释变量Y 看成是解释变量X 的函数是前提是，在其它条件不变的情况下，并且，所有其它影响Y 的因素都应与X 不相关，但这在实际情况中很难满足。

怎样在一元线性回归的基础上引入多元变量的回归？ 看教科书第72—73页关于汽车销售量的影响因素的讨论。

一、多元线性回归模型的意义1、建立多元线性回归模型的意义，即一元线性回归模型的缺陷，多个主要影响因素的缺失对模型的不利影响。

在一元线性回归模型中，如果总体回归函数的设定是正确的，那么，根据样本数据得到的样本回归模型就应该有较好的拟合效果，这时，可决系数就应该较大。

相反，如果在模型设定时忽略了影响被解释变量的某些重要因素，拟合效果可能就会较差，此时可决系数会偏低，并且由于忽略了一些重要变量而对误差项的影响会加大，这时误差项会表现出一些违背假定的情况。

2、从一个解释变量到多个解释变量的演变。

一个生产函数的例子，一个商品需求函数的例子，（教材第74页）。

二、多元线性回归模型及其矩阵表示1、一般线性回归模型的数学表达式。

设 12233i ii k k ii Y XXXu ββββ=+++++i=1，2，3，…，n在模型表达式里，1β仍是截距项，它反映的是当所有解释变量取值为零时，被解释变量Y 的取值；j β（j=2，3，…，k ）为斜率系数，它的经济含义：在其它变量不变的情况下，第j 个解释变量每变动一个单位，Y 平均增加（或减少）j β个单位，这就是所谓的运用边际分析法对多元变量意义下回归参数的解释。

因此，称j β为偏回归系数，它反映了第j 个解释变量对Y 的边际影响程度。

4、2、总体回归函数，即12233(|)i i i k ki E Y X X X X ββββ=++++3、样本回归函数，即12233ˆˆˆˆˆi i k k iY X X Xββββ=++++ 4、将n 个样本观测值代入上述表达式，可得到从形式上看，像似方程组的形式。

第三章多元线性回归模型课件

第三章多元线性回归模型课件
的元素
故有：βˆ j ~ N ( β j , σ 2c jj ) j 1, 2,..., k
3、估计量的性质
多元回归中σ 2 的无偏估计为：
σˆ2
ei2
或表示为 σˆ2 ee
n-k -1
n-k 1
将 βˆk 作标准化变换：
zk
βˆk - βk SE( βˆk )
βˆk σ
- βk c jj
给定显著性水平 ，查F分布表得临界值 F (k, n - k 1)
并通过样本观测值计算 F 值
▼如果 F F (k,n - k 1) (小概率事件发生了) 则拒绝 H0 : β2 = β3 = ...= βk = 0 ，说明回归模型 有显著意义，即所有解释变量联合起来对
（如收入、价格、费用、道路状况、能源、政策环境等）
各种因素对汽车销量影响的性质怎样？（正、负） 各种因素影响汽车销量的具体数量关系是什么？ 所得到的数量结论是否可靠？ 中国汽车行业今后的发展前景怎样？应当如何制定汽车的 产业政策？ 很明显，只用一个解释变量已很难分析汽车产业的发展, 还需要寻求有更多个解释变量情况的回归分析方法。
x1i yi βˆ 2
x2i yi ... βˆ k yi2
xki yi
证明详见附录A.3
可决系数
R 2 ESS 1 RSS TSS TSS
• 该统计量越接近于1，模型的拟合优度越高。
• 从R2的表达式中发现，如果在模型中增加解释 变量， R2往往增大。
这就给人一个错觉：要使得模型拟合得好，只 要增加解释变量即可。
u1
u
u2
un
X1k
X
2k
X nk
1、模型的数学形式
总体回归函数 E(Y) = Xβ 或 Y = Xβ + u

第3章 多元线性回归模型

第3章 多元线性回归模型

TSS
TSS
该统计量越接近于1，模型的拟合优度越高。
问题：在应用过程中发现，如果在模型中增加一个解 释变量， R2往往增大（Why?)
因为残差平方和往往随着解释变量个数的增加而减少。
这就给人一个错觉：要使得模型拟合得好，只要增加 解释变量即可。—— 但是，现实情况往往是，由增加 解释变量个数引起的R2的增大与拟合好坏无关，因此在 多元回归模型之间比较拟合优度，R2 就不是一个合适 的指标，必须加以调整。
所以，在多元线性回归模型中，依然有
n
n
即
yi2 （[ Yˆi Y） ei ]2
i 1
i 1
n
n
n
（Yˆi Y）2 ei2 2 e（i Yˆi Y）
i 1
i 1
i 1
n
n
（Yˆi Y）2 ei2
i 1
i 1
（3-20）
TSS ESS RSS
（3-21）
可决系数
R 2 ESS 1 RSS
μ~ N(0, 2I)
假设5，回归模型的设定是正确的。
第二节 多元线性回归模型的 参数估计
任务
模型结构参数 0 、1、2 、L 、k 的估计
随机误差项的方差 2 的估计
方法
普通最小二乘法
内容
一、参数的普通最小二乘估计 二、参数的普通最小二乘估计量的性质 三、普通最小二乘样本回归函数性质 四、随机误差项的方差的普通最小二乘估计 五、样本容量问题
第三章 经典单方程计量经济学模型： 多元线性回归模型
• 多元线性回归模型 • 多元线性回归模型的参数估计 • 多元线性回归模型的统计检验 • 多元线性回归模型的预测
§3.1 多元线性回归模型
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章多元线性回归模型
前一章讲的简单线性回归模型，主要讨论的是一个应变量和一个解释变量之间的线性关系。

而在实际的经济问题中，一个经济变量往往同多个经济变量相联系。

比如，我们前面一直在举的例子：说消费支出与收入有关，而在实际生活中，消费支出同时又会与家庭的财富总量有关，还可能会与所处的年龄段、性别、所受教育程度等因素有关。

所以，我们有必要将一个解释变量的情况推广到多个解释变量。

利用多元回归方法进行分析/
第一节多元线性回归模型及古典假定
一、多元线性回归模型
1、多元线性回归模型的一般形式：
总体回归方程：E（Y│X1，X2，…Xk）=β0+β1X1+β2X2+β3X3+…+βkXk
Y=β0+β1X1+β2X2+β3X3+…+βkXk+µ
样本回归方程：Y=β0+β1X1+β2X2+β3X3+…+βkXk
Y=β0+β1X1+β2X2+β3X3+…+βkXk+e
2、回归系数的经济意义：
简单线性回归中的回归系数的经济意义：如 Y=50.78+0.86X 系数代表每增加一元收入,消费支出要增加0.86元
多元线性回归中的回归系数的经济意义:由于多个解释变量会同时对应变量的变动发挥作用,因此,如果我们要考察其中某个解释变量对应变量的影响,就必须使其他解释变量保持不变来进行分析.所以,模型中的单个回归系数βj就表示当控制其他解释变量不变的条件下,第j个解释变量的单位变动对应变量均值的影响.
多元线性回归模型中这样的回归系数,称为偏回归系数。

与简单线性回归分析一样，多元线性回归分析要解决的主要问题仍是：根据观测样本估计模型中的各个参数；对估计的参数及回归方程进行统计检验；利用回归模型进行预测和经济分析。

二、模型的古典假定
在回归分析中，为了使所作出的估计具有较好的统计性质，我们对模型中的随机扰动项和解释变量作出一些假定。

多元线性回归模型的假定条件有：
假定1：零均值假定: 即假定随机扰动项彻底均值为零E（μi）= 0
假定2：同方差假定: μi 的方差为某个相同的常数Var（μi）=σ2
假定3：无自相关假定: 随机扰动项μi的逐次值互不相关
Cov(μi , μj )=0 （i≠j）
假定4：随机扰动项μi与解释变量Xi 不相关。

Cov(μi ,Xi )=0
假定5：正态性假定，即假定μi服从均值为零、方差为σ2的正态分布u~ N (0, σ2)
假定6：无多重共线性假定：即假定各解释变量之间不存在线性关系，或者说各解释变量的观测值之间线性无关。

（这是多元线性回归模型与简单线性回归模型基本假定的区别）
多元线性回归模型参数所采用的最小二乘法估计思路以及估计的性质都与简单线性回归模型参数的估计是类似的，由于采用了矩阵，计算过程比较复杂，我们就省略了，因为实际操作过程中，这部分可以由软件代劳了。

第二节多元线性回归模型的检验
一、拟合优度检验
在简单线性回归模型中，我们用可决系数r2来衡量估计模型对观测值的拟合程度。

在多元线性回归模型中，我们也需要讨论所估计的模型对观测值的拟合程度。

1、多重可决系数
R2=ESS/TSS=1—RSS/TSS
大小意义
在应用过程中，人们发现R2的大小对于解释变量的数目容易作出灵敏的反映。

也就是说，随着模型中解释变量的增多，多重可决系数的值往往会变大，从而增加模型的解释功能。

这给人们一个错觉：要使模型拟合得好，就必须增加解释变量。

但是，在样本容量一定的情况下，增加解释变量必定使得待估计参数的个数增加，从而损失自由度（n—k—1）（回忆我们说的区间估计，置信区间，随着自由度的减小，临界值增大，置信区间增大，估计的精度降低）
而且，在实际应用中，有时所增加的解释变量并非必要，违背了我们尽可能采用最简单形式的原则。

因此，在比较应变量相同而解释变量个数不同的两个模型的拟合程度时，不能简单地比较多重可决系数。

为此，人们引入了修正可决系数：R2=1—RSS/（n-k-1）/TSS/（n-1）
修正的思路就是用平方和的自由度，消除可决系数对解释变量个数的依赖度。

多重可决系数与修正可决系数的关系是：
修正可决系数的性质：
（1）若K≥1，则R2≤R2
（2）修正可决系数可能出现负值。

如n=10，k=2，R2=0.1时，R2=—0.157.显然,负的拟合优度没有任何意义,在这种情况下,我们取R2=0
（3）在实际应用中,我们往往希望所建模型的R2和R2越大越好,但它们越大,只说明列入模型中的解释变量对应变量联合影响程度越大,并不能说明模型中各个解释变量对应变量的影响程度显著.
二、回归参数的显著性检验(t检验)
目的:在与检验当其他解释变量不变时,该回归系数对应的解释变量是否对应变量有显著影响。

检验方法与简单线性回归模型的检验基本相同。

三、回归方程的显著性检验（F检验）
与简单线性回归方程一样，方程的显著性检验，目的是判断模型中的多个解释变量同应变量之间是否存在显著的线性关系。

即对回归系数进行整体检验。

四、简单线性回归模型中的T检验与F检验的关系与多元线性回归方程中的有和区别：
简单线性回归模型中的T检验与F检验结果是一致的；
多元线性回归方程中的T检验与F检验的结果有可能不一致。

多元线性回归模型的预测与简单线性回归模型是类似的，同样包括对应变量均值和个别值的预测，其中又分点预测和区间预测。