应用EViews进行Chow检验法
- 格式:docx
- 大小:71.83 KB
- 文档页数:2
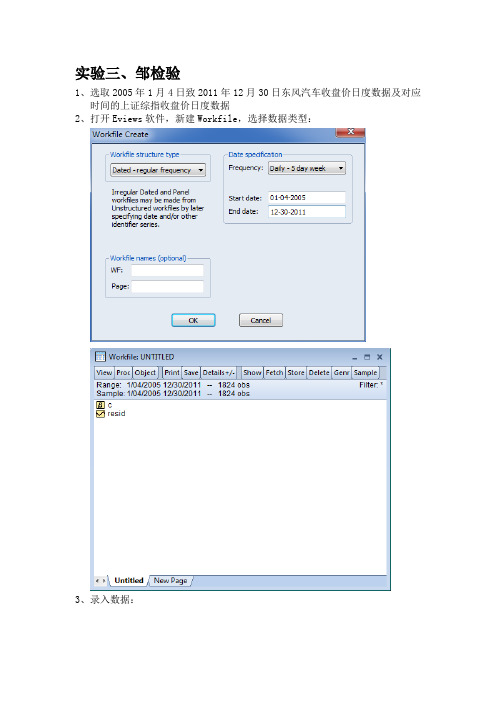
实验三、邹检验1、选取2005年1月4日致2011年12月30日东风汽车收盘价日度数据及对应时间的上证综指收盘价日度数据2、打开Eviews软件,新建Workfile,选择数据类型:3、录入数据:对两个收盘价数据进行处理,计算每天的收益率,定义为:rd和rs genr rd=(df-df(-1))/df(-1)genr rs=(sz-sz(-1))/sz(-1)4、对rd和rs做回归分析,ls rd c rs:Dependent Variable: RDMethod: Least SquaresDate: 06/22/14 Time: 19:13Sample (adjusted): 1/05/2005 7/12/2011Included observations: 1700 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.C 9.57E-05 0.000450 0.212485 0.8318RS 1.077154 0.024237 44.44232 0.0000R-squared 0.537723 Mean dependent var 0.000644 Adjusted R-squared 0.537450 S.D. dependent var 0.027301 S.E. of regression 0.018567 Akaike info criterion -5.133649 Sum squared resid 0.585379 Schwarz criterion -5.127251 Log likelihood 4365.601 Hannan-Quinn criter. -5.131280 F-statistic 1975.120 Durbin-Watson stat 1.858855 Prob(F-statistic) 0.000000rs系数的P值为0,说明rd与rs存在显著的线性关系。

数学与统计学院实验报告院(系):数学与统计学学院学号:姓名:实验课程:计量经济学指导教师:实验类型(验证性、演示性、综合性、设计性):验证性实验时间:2017年 3 月15 日一、实验课题Chow检验(邹氏检验)二、实验目的和意义1 建立财政支出模型表1给出了1952-2004年中国财政支出(Fin)的年度数据(以1952年为基期,用消费价格指数进行平减后得数据)。
试根据财政支出随时间变化的特征建立相应的模型。
表1obs Fin obs Fin obs Fin1952 173.94 1970 563.59 1988 1122.881953 206.23 1971 638.01 1989 1077.921954 231.7 1972 658.23 1990 1163.191955 233.21 1973 691 1991 1212.511956 262.14 1974 664.81 1992 1272.681957 279.45 1975 691.32 1993 1403.621958 349.03 1976 656.25 1994 1383.741959 443.85 1977 724.18 1995 1442.191960 419.06 1978 931.47 1996 1613.191961 270.8 1979 924.71 1997 1868.981962 229.72 1980 882.78 1998 2190.31963 266.46 1981 874.02 1999 2616.461964 322.98 1982 884.14 2000 3109.611965 393.14 1983 982.17 2001 3834.161966 465.45 1984 1147.95 2002 4481.41967 351.99 1985 1287.41 2003 5153.41968 302.98 1986 1285.16 2004 6092.991969 446.83 1987 1241.86步骤提示:(1)做变量fin的散点图,观察规律,看在不同时期是否有结构性变化。

数学与统计学院实验报告院(系):数学与统计学学院学号:姓名:实验课程:计量经济学指导教师:实验类型(验证性、演示性、综合性、设计性):验证性实验时间:2017年 3 月 15 日一、实验课题Chow检验(邹氏检验)二、实验目的和意义1 建立财政支出模型表1给出了1952-2004年中国财政支出(Fin)的年度数据(以1952年为基期,用消费价格指数进行平减后得数据)。
试根据财政支出随时间变化的特征建立相应的模型。
表1obs Fin obs Fin obs Fin19521970198819531971198919541972199019551973691199119561974199219571975199319581976199419591977199519601978199619611979199719621980199819631981199919641982200019651983200119661984200219671985200319681986200419691987步骤提示:(1)做变量fin的散点图,观察规律,看在不同时期是否有结构性变化。
(2)建立时间变量t=1,2,…,做Fin关于t的线性回归模型,并对其做参数结构稳定性检验(Chow检验或Chow预测检验)(建立变量t的方法是:t=@trend()+1)三、解题思路(1)Eviews6---建立fin的连续序列(object--series)---画散点图(view—graph—dot plot)(2)建立t的时间变量(quick—generate series—t=@trend()+1)---建立fin、t的方程(quick--estimate equation—fin c t)---chow检验(view—stability test—chow breakpoint test—断点为1996)---建立三个方程(一个受约束方程,两个不受约束方程)---比较1996年属于不受约束方程那个方程四、实验过程记录与结果(1)、散点图通过散点图可以发现,1996年存在结构性变化(针对斜率96年前后突然变大)(2)chow检验受约束模型:由该方程发现,残差存在明显的相关性,即存在自相关性,进行以1996年为断点分阶段检验不受约束模型(1)、1952-1996(2)1997-2004根据受约束模型相比,各统计量明显有转好的趋势。

操作步骤1.建立工作文件(1)建立数据的exel电子表格(2)将电子表格数据导入eviewsFile-open-foreign data as workfile,得到数据的Eviews工作文件和数据序列表。
2.计算变量间的相关系数在窗口中输入命令:cor coilfuture dow shindex nagas opec ueurope urmb,点击回车键,得到各序列之间的相关系数。
结果表明Coilfuture数列与其他数列存在较好的相关关系。
3.时间序列的平稳性检验(1)观察coilfuture序列趋势图在eviews中得到时间序列趋势图,在quick菜单中单击graph,在series list对话框中输入序列名称coilfuture,其他选择默认操作。
图形表明序列随时间变化存在上升趋势。
(2)对原序列进行ADF平稳性检验quick-series statistics-unit root test,在弹出的series name对话框中输入需要检验的序列的名称,在test for unit root in 选择框中选择level,得到原数据序列的ADF检验结果,其他保持默认设置。
得到序列的ADF平稳性检验结果,检测值0.97大于所有临界值,则表明序列不平稳。
以此方法,对各时间序列依次进行ADF检验,将检验值与临界值比较,发现所有序列的检验值均大于临界值,表明各原序列都是非平稳的。
(3)时间序列数据的一阶差分的ADF检验quick-series statistics-unit root test,在series name对话框中输入需要检验的序列的名称,在test for unit root in 选择框中选择1nd difference,对其一阶差分进行平稳性检验,其他保持默认设置。
得到序列的ADF平稳性检验结果,检测值-7.8远小于所有临界值,则表明序列一阶差分平稳。
以此方法,对各时间序列的一阶差分依次进行ADF检验,将检验值与临界值比较,发现所有序列的检验值均小于临界值,表明各序列一阶差分都是平稳的。

我用的是Eviews3.1注册版(因为其他的版本没注册都不稳定容易自己关闭程序),但大抵操作应该是相同的。
首先建立新的workfile,在命令窗口输入series,弹出新建的数列窗口,把要检验的数据存进去。
然后再数列窗口下点击view,找到unit root test就是单位根检验,弹出来的窗口的左上角是选择检验方式,一般保持默认的DF那一项就好了,Eviews里面的这个DF选项是把DF与ADF检验都包括在一起了。
右边的intercept啦intercept and trend啦是针对ADF 检验的不同模型,如果搞不清楚干脆就按默认吧。
左下角的level,1st differential,2st什么的是问你是针对原始数据、还是一阶差分、二阶差分来做检验,默认是level,就是原始数据。
都选好之后点击OK就好了。
输出的结果主要是看上面的表,第一个表左边给出一个值,右边给了三个值,分别是置信度99%,95%,90%的ADF检验临界值。
左边的值如果小于右边的某个值,说明该数据落在右边那个对应值的置信区间里。
比如左边给出-3,右边对应95%置信度的值是-1,-3<-1所以数据不存在单位根,是平稳的,这一检验的置信度是95%。
大概是这样吧,具体的ADF模型选择等等最好看一看相关书籍。
Eviews不难学的~~嘿嘿我也就是三天恶补大概看完的。
ADF检验的原假设是存在单位根,一般EVIEWS输出的是ADF检验的统计值,只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设,认为数据平稳。
注意,ADF值一般是负的,也有正的,但是它只有小于1%水平下的才能认为是及其显著的拒绝原假设这样的话,如果你的变量是水平变量。
那么,你需要取对数,一般来说,取对数后的变量一般是平稳的,这样,你无需作协整;如果对数变量非平稳,再取一阶差分(绝大多数的水平变量取对数后再一阶差分是平稳的),你就可以作协整了了。
如果你的变量已是相对数,xt 与yt 并非I(1),那么,不能作协整,仅作一般的时间序列分析即可。

应用EViews进行Chow检验法(兰州财经大学金融学院 14级金融工程2班王满全)数据:1992-12-31,,2016—12-31中国GDP(单位:亿元)和INDEX为了分析中国INDEX和GDP的关系,根据上表做如下散点图:从散点图可以看出INDEX和GDP大体呈线性关系,为分析中国INDEX随GDP变动的数量规律性,可建立简单回归模型。
第一步:构建回归模型。
其中:——INDEX;——GDP应用EViews软件进行数据处理,得到如下回归结果:对回归结果的几点说明:1.经济意义:所估计的参数â=1085。
150,=0。
003287,说明GDP每增加1亿元,可导致INDEX平均增加0。
003287点。
2.拟合优度:R-squared=0.445876说明所建模型整体上对样本数据拟合可以,即解释变量GDP对被解释变量INDEX的部分差异做出了解释。
3.回归系数的t检验:取,因为t(â)=4。
101768〉,t()=4.301969〉,所以可得出GDP对INDEX确有影响。
4.F值(模型总体显著性检验的指标,数值越大,模型越好):因为Prob(F-ststistic)=0。
000265<0。
01,所以通过了0.01水平的显著性检验,说明模型总体显著。
5.Durbin—Watson检验:因为<Durbin—Watson stat=1。
572790<,所以不拒绝零假设,并且没有显著的残差自相关。
第二步:进行Chow氏稳定性检验。
第三步:确定结构变化的转折点(如2004年12月31日),进行检验。
可得:从输出结果看,发现在0.1的水平上拒绝模型稳定原假设,说明2004年12月31日以后的中国股市发生了结构性变化.。
数学与统计学院实验报告院(系):数学与统计学学院学号:姓名:实验课程:计量经济学指导教师:实验类型(验证性、演示性、综合性、设计性):验证性实验时间:2017年 3 月15 日一、实验课题Chow检验(邹氏检验)二、实验目的和意义1 建立财政支出模型表1给出了1952-2004年中国财政支出(Fin)的年度数据(以1952年为基期,用消费价格指数进行平减后得数据)。
试根据财政支出随时间变化的特征建立相应的模型。
表1obs Fin obs Fin obs Fin1952 173.94 1970 563.59 1988 1122.881953 206.23 1971 638.01 1989 1077.921954 231.7 1972 658.23 1990 1163.191955 233.21 1973 691 1991 1212.511956 262.14 1974 664.81 1992 1272.681957 279.45 1975 691.32 1993 1403.621958 349.03 1976 656.25 1994 1383.741959 443.85 1977 724.18 1995 1442.191960 419.06 1978 931.47 1996 1613.191961 270.8 1979 924.71 1997 1868.981962 229.72 1980 882.78 1998 2190.31963 266.46 1981 874.02 1999 2616.461964 322.98 1982 884.14 2000 3109.611965 393.14 1983 982.17 2001 3834.161966 465.45 1984 1147.95 2002 4481.41967 351.99 1985 1287.41 2003 5153.41968 302.98 1986 1285.16 2004 6092.991969 446.83 1987 1241.86步骤提示:(1)做变量fin的散点图,观察规律,看在不同时期是否有结构性变化。
应用EViews进行Chow检验法
(兰州财经大学金融学院14级金融工程2班王满全)数据:1992-12-31,⋯,2016-12-31中国GDP(单位:亿元)和INDEX
为了分析中国INDEX和GDP的关系,根据上表做如下散点图:
从散点图可以看出INDEX和GDP大体呈线性关系,为分析中国INDEX随GDP变动的数量规律性,可建立简单回归模型。
第一步:构建回归模型。
Y t=α+βX t+u t
其中:Y t——INDEX;X t——GDP
应用EViews软件进行数据处理,得到如下回归结果:
对回归结果的几点说明:
1.经济意义:所估计的参数â=1085.150,β=0.003287,说明GDP每增加1亿元,
可导致INDEX平均增加0.003287点。
2.拟合优度:R-squared=0.445876说明所建模型整体上对样本数据拟合可以,
即解释变量GDP对被解释变量INDEX的部分差异做出了解释。
3.回归系数的t检验:取α=0.05,因为t(â)=
4.101768>t0.025(25−2)=2.069,
t(β)=4.301969>t0.025(25−2)=2.069,所以可得出GDP对INDEX确有影响。
4.F值(模型总体显著性检验的指标,数值越大,模型越好):因为Prob(F-ststistic)
=0.000265<0.01,所以通过了0.01水平的显著性检验,说明模型总体显著。
5.Durbin-Watson检验:因为d u=1.21<Durbin-Watson stat=1.572790<4−d u=
2.79,所以不拒绝零假设,并且没有显著的残差自相关。
第二步:进行Chow氏稳定性检验。
第三步:确定结构变化的转折点(如2004年12月31日),进行检验。
可得:
从输出结果看,发现在0.1的水平上拒绝模型稳定原假设,说明2004年12月31日以后的中国股市发生了结构性变化。