高一数学周周练一

心尺引州丑巴孔市中潭学校一中高一数学2021春学期第十九周双休练习班级 成绩一、填空题〔本大题共14小题，每题5分，共70分。

请把答案填写在答题卡相应的位置上．．．．．．．．．.〕1、不等式(1)(2)0x x --<的解集是 ▲ 。

2、数列：1111,,,12233445--⨯⨯⨯⨯，……的一个通项公式为 ▲ 。

3、不等式003x y x y x -≥⎧⎪+≥⎨⎪≤⎩表示的区域面积为 ▲ 。

4、等比数列}{n a 中，340,2na a a >=，那么212226log log log a a a +++= ▲ 。

5、假设关于x 不等式2210xax ++≥的解集为R ，那么实数a 的取值范围是 ▲ 。

6、函数cos 2tan sin y ααα=+，(0,)2πα∈的最小值为 ▲ 。

7、将一颗骰子先后抛掷2次，那么向上的点数之和为3的倍数的概率为 ▲ 。

8、ABC ∆的外接圆半径为1，那么sin sin sin a b c A B C+-=+- ▲ 。

9、在ABC ∆中，2cos c a B =,那么ABC ∆的形状为 ▲ 。

10、}{n a 为等差数列，{}n b 为正项等比数列，其公比1q≠，假设111111,a b a b ==，那么66,a b 的大小关系为 ▲ 。

11、数列}{n a 的通项为224nn a n =+，那么}{n a 的最大项是第 ▲ 项。

12、假设0,0,2a b a b >>+=，那么以下不等式对一切满足条件的,a b 恒成立的是 ▲ 。

①1ab ≤；+≤； ③ 222a b +≥；④333a b +≥； ⑤112a b+≥ 13、正数数列{n a }的前n 项和为n S，且1n a =+,(*n N ∈),那么n a = ▲ 14、假设关于x 的不等式22(21)x ax -≤的解集中的整数恰有2个，那么实数a 的取值范围是 ▲ ．一中高一数学2021春学期第十九周双休练习答题卡1、__________________ 6、__________________ 11、________________2、__________________ 7、__________________ 12、________________3、__________________ 8、__________________ 13、________________4、_________________ 9、_________________ 14、________________5、_________________ 10、_________________二、解答题〔本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤〕15、〔此题总分值14分〕{}n a 是公差不为零的等差数列，11a =，且139,,a a a 成等比数列.〔1〕求数列{}n a 的通项公式;〔2〕求数列{}n a 的前n 项和n S 。

高一数学周周练（1）（角的概念·弧度制共150分） 学生__________一、选择题（每小题5分，共60分）1．下列命题中的真命题是（ ）A ．三角形的内角是第一象限角或第二象限角 C ．第二象限的角比第一象限的角大B ．第一象限的角是锐角 D ．角α是第四象限角的充要条件是2k π－2π＜α＜2k π(k ∈Z ) 2．设k ∈Z ，下列终边相同的角是（ ）A ．（2k +1）·180°与（4k ±1）·180°B ．k ·90°与k ·180°+90°C ．k ·180°+30°与k ·360°±30°D ．k ·180°+60°与k ·60°3．已知弧度数为2的圆心角所对的弦长也是2，则这个圆心角所对的弧长是（ ）A ．2B ．1sin 2 C ．1sin 2 D ．2sin 4．一钟表的分针长10 cm ，经过35分钟，分针的端点所转过的长为：（ ） A ．70 cm B ．670 cm C ．(3425-3π)cm D ．3π35 cm 5．若90°＜－α＜180°，则180°－α与α的终边（ ）A ．关于x 轴对称B ．关于y 轴对称C ．关于原点对称D ．以上都不对6．若角α终边上有一点P （－3，0），则下列函数值不正确的是（ ） A ．si n α=0B ．cos α=－1C ．ta n α=0D ．cot α=0 7．某扇形的面积为12cm ，它的周长为4cm ，那么该扇形圆心角的度数为（ ）A ．2°B ．2C ．4°D ．48．中心角为60°的扇形，它的弧长为2π，则它的内切圆半径为 （ ）A ．2B ．3C ．1D ．23 9．如果弓形的弧所对的圆心角为3π，弓形的弦长为4 cm ，则弓形的面积是：（ ） A ．（344-9π） B ．（344-3π ） C ．（348-3π） D ．（328-3π） 10.若α是第三象限角，则下列四个三角函数式中一定为正数的是（ ） A ．sin α+cos α B ．tan α+sin α C ．sin α·sec α D ．cot α·sec α11.1sin 、1cos 、1tan 的大小关系为（ ）A ．1tan 1cos 1sin >>B ．1cos 1tan 1sin >> C ．1cos 1sin 1tan >> D ．1sin 1cos 1tan >> 12．设集合M ={α|α=k π±6π，k ∈Z }，N ={α|α=k π+(－1)k 6π，k ∈Z }那么正确的是（ ） A ．M =N B ．M N C ．N M D ．M N 且N M第Ⅱ卷（非选择题，共90分）二、填空题（每小题5分，共20分）13．若角α是第三象限角，则2α角的终边在 . 14．与－1050°终边相同的最小正角是 .15．已知α是第二象限角，且,4|2|≤+α则α的范围是 .16．已知扇形的周长为20 cm ，当扇形的中心角为多大时，它有最大面积，最大面积是三、解答题（本大题共70分）17．用集合表示下列终边落在阴影部分的角。

高一数学“每周一练”系列试题及答案
1．某初级中学领导采用系统抽样方法，从该校预备年级全体800名学生中抽50名学生做牙
齿健康检查。

现将800名学生从1到800进行编号，求得间隔数k
800
50
=16
，即每16
人抽取一个人。

在1~16中随机抽取一个数，如果抽到的是7，则从33 ~ 48这16个数中应取的数是（）
A．40．B．39．C．38．D．37．
2．某工厂有工人1 000名，其中250名工人参加过短期培训(称为A类工人)，另外750名工人参加过长期培训(称为B类工人)．现用分层抽样方法(按A类，B类分二层)从该工厂的工人中共抽查100名工人，调查他们的生产能力(生产能力指一天加工的零件数)．
(1)A类工人中和B类工人中各抽查多少工人？
(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.
生产能
力分组
[100,110)[110,120)[120,130)[130,140)[140,150) 人数48x 5 3 生产能
力分组
[110,120)[120,130)[130,140)[140,150) 人数6y 3618
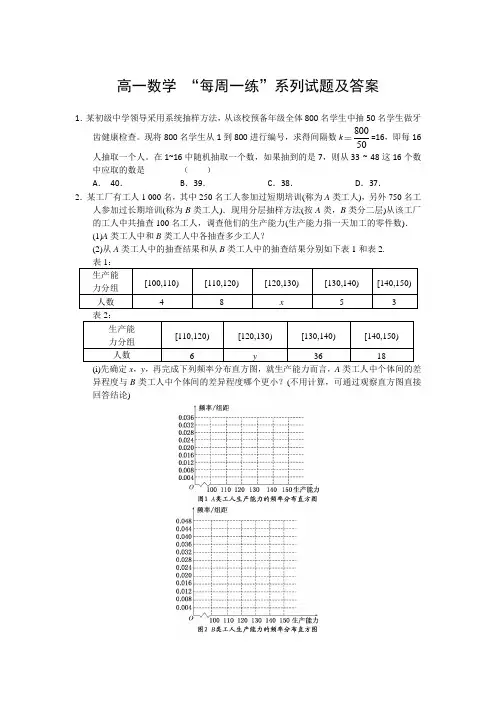
(i)先确定x，y，再完成下列频率分布直方图，就生产能力而言，A类工人中个体间的差
异程度与B类工人中个体间的差异程度哪个更小？(不用计算，可通过观察直方图直接回答结论)。

高一数学下册每周一练测试题及答案高一数学“每周一练”系列试题（39）一、选择题：本大题共10小题，每小题2分，满分20分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1、设A＝，U=R，求 =( ) A、 B、 C、 D、 2、设集合A＝{x|－5≤x＜1}，B＝{x|x≤2}，则A B＝（） A．{x|－5≤x＜1} B．{x|－5≤x≤2} C．{x|x＜1} D．{x|x≤2} 3、已知全集U＝{0，1，2，3}且＝{2}，则集合A的真子集共有（）A．3个 B．5个 C． 8个D．7个 4、下列四句话中：① ＝｛0｝；②空集没有子集；③任何一个集合必有两个或两个以上的子集；④空集是任何一个集合的子集．其中正确的有（） A．0个 B．1个 C．2个 D．3个 5、若集合M= ， , 则下面结论中正确的是（） A. B. C. D. 6、下列函数中是奇函数的是( D ) A、 B、 C、 D、 7、下列函数与表示同一函数的是（） A. B. C. D. 8、已知，则的值为（） A、100 B、10 C、－10 D、－100 9、函数y=-x+a与y=a-x (其中a＞0且a≠1) 在同一坐标系中的图象可能为（）A． B． C． D． 10、已知，，，则下列关系中正确的是（）Ａ．Ｂ．Ｃ．Ｄ．二、填空题: 本大题共5小题，每小题5分，满分25分． 11、函数的递增区间是＝ 12、在平面直角坐标系中，角的终边关于一、三象限的角平分线对称，且角的终边经过点，则＝ 13、如图，菱形ABCD的边长为1，，E、F分别为AD、CD的中点，则＝ 14、已知函数是定义在上的奇函数，且当时，，则＝ . 15、已知函数，对于上的任意有如下条件：① ；② ③ ，其中能使恒成立的条件是（填写序号）三、解答题：本大题共6小题，共75分。

解答须写出文字说明，证明过程或演算步骤． 16、（本题14分）已知全集，， . （1）用列举法表示集合（2）求，，。

高中数学必修一周周练（第一周）一、选择题1．①某班视力较好的同学；②方程x 2－1＝0的解集；③漂亮的花儿；④空气中密度大的气体．其中能组成集合的是( )A. ②B. ①③C. ②④D. ①②④2、由a 2,2－a,4组成一个集合A ，A 中含有3个元素，则实数a 的取值可以是( )A. 1B. －2C. 6D. 23、设集合A ＝⎭⎬⎫⎩⎨⎧∈=N n x x n ,31，若x1∈A ，x 2∈A ，则必有( )A. x 1＋x 2∈AB. x 1x 2∈AC. x 1－x 2∈AD. x1x 2∈A 4．已知集合A ＝{x |x 2＋4x ＋3≤0}，B ＝{x |x 2－ax ≤0}，若A ⊆B ，则实数a 的取值范围是() A. [－3,3] B. [0，＋∞) C. (－∞，－3] D. R5、若函数f (x )＝ax 2－1，a 为一个正常数，且f (f (－1))＝－1，那么a ＝( )A. 1B. 0C. －1D. 26．下列各组函数表示相等函数的是( )A. f (x )＝⎩⎪⎨⎪⎧ x ， x >0，－x ， x <0与g (x )＝|x |B. f (x )＝2x ＋1与g (x )＝2x 2＋x xC. f (x )＝|x 2－1|与g (t )＝(t 2－1)2D. f (x )＝x 2与g (x )＝x二、填空题7、已知集合A 由方程(x －a )(x －a ＋1)＝0的根构成，且2∈A ，则实数a ＝________.8、由实数t ，|t |，t 2，－t ，t 3所构成的集合M 中最多含有________个元素．9设集合A ＝{x |－1<x <2}，B ＝{x |x <a }，若A ∩B ≠∅，则a 的取值范围是________．10、若[a,3a －1]为一确定区间，则a 的取值范围是________．三、解答题11、已知集合A 是由a －2,2a 2＋5a,12三个元素组成的，且－3∈A ，求a 的值．12、设S 是由满足下列条件的实数所构成的集合：①1∉S ；②若a ∈S ，则11－a ∈S .请回答下列问题：(1)若2∈S ，则S 中必有另外两个数，求出这两个数；(2)求证：若a ∈S ，则1－1a∈S ； (3)在集合S 中元素能否只有一个？若能，把它求出来；若不能，请说明理由．13、若集合A ＝{x |x 2＋x －6＝0}，B ＝{x |x 2＋x ＋a ＝0}，且B ⊆A ，求实数a 的取值范围．14、已知集合A ＝{x |1<ax <2}，B ＝{x |－1<x <1}，求满足A ⊆B 的实数a 的取值范围．。

汝城一中高一数学周周练（1）满分：150分 时量：120分钟注 意：交卷时只交答卷一、选择题：每小题5分，共50分，每小题有且只有一个正确答案。

1．设集合P=｛立方后等于自身的数｝，那么集合P 的真子集个数是A ．3B ．4C ．7D ．8 2．如果偶函数在],[b a 具有最大值，那么该函数在],[a b --有 A ．最大值 B ．最小值 C ．没有最大值 D ． 没有最小值3．下列各组函数中，表示同一函数的是A ．xx y y ==,1 B ．y y ==C ．33,x y x y ==D ． 2)(|,|x y x y == 4．函数b x k y ++=)12(在实数集上是增函数，则A ．21->k B ．21-<k C ．0>b D ．0>b 5．函数px x x y +=||，R x ∈是 A ．偶函数B ．奇函数C ．不具有奇偶函数D ．与p 有关6．设全集}7,6,5,4,3,2,1{=U ，集合}5,3,1{=A ，集合}5,3{=B ，则 A ．B A U ⋃= B ． B A C U U ⋃=)( C ．)(B C A U U ⋃= D ．)()(B C A C U U U ⋃=7．已知集合 },61|{Z m m x x M∈+==，},312|{Z n n x x N ∈-==，=P x x |{+=2p },61Z p ∈，则P N M ,,的关系A ．N M =PB ．M PN =C ．M N PD ． N P M8．图中阴影部分所表示的集合是A.B ∩［C U (A ∪C)］B.(A ∪B) ∪(B ∪C)C.(A ∪C)∩(C U B)D.［C U (A ∩C)］∪B9．已知g (x )=1-2x, f [g (x )]=)0(122≠-x xx , 则f (21)等于 A ．1B ．3C ．15D ．3010．定义在R 上的偶函数)(x f ，满足)()1(x f x f -=+，且在区间]0,1[-上为递增，则A ．)2()2()3(f f f <<B ．)2()3()2(f f f <<C ．)2()2()3(f f f <<D ．)3()2()2(f f f <<二、填空题：每小题5分，共25分，将正确答案填在横线上。

智才艺州攀枝花市创界学校淳中高一数学周周练试题一．选择题〔每一小题5分，一共50分〕1．⎭⎬⎫⎩⎨⎧∈+==Z k k x x M ,412|，⎭⎬⎫⎩⎨⎧∈+==Z k k x x N ,214|，那么〔〕 〔A N M =〔B 〕M N 〔C 〕N M 〔D 〕N M ⊆ 2．设全集{}+∈≤=N x x x U ,8|，假设{}8,1)(=⋂B C A U ，{}6,2)(=⋂B A C U ， {}7,4)()(=⋂B C A C U U ，那么〔〕〔A 〕{}{}6,2,8,1==B A 〔B 〕{}{}6,5,3,2,8,5,3,1==B A 〔C 〕{}{}6,5,3,2,8,1==B A 〔D 〕{}{}6,5,2,8,3,1==B A3．集合{}01|2=++=x m x x A ，假设Φ=⋂R A ，那么实数m 的取值范围是〔〕 〔A 〕4<m 〔B 〕4>m 〔C 〕40<<m 〔D 〕40<≤m4．假设关于x 的不等式|x+2|+|x-1|<a 的解集为φ，那么a 的取值范围是 〔〕 〔A 〕〔3，+∞〕〔B 〕[3，+∞〕 〔C 〕〔-∞，3] 〔D 〕〔-∞，3〕 5．设P=}|),{(},|{22x y y x Q x y x ===，那么P 、Q 的关系是〔〕 〔A 〕P Q 〔B 〕P Q 〔C 〕P=Q 〔D 〕P Q=Φ 6．以下四组函数，表示同一函数的是〔〕〔A 〕f (x )＝2x ,g (x )＝x 〔B 〕f (x )＝x ,g (x )＝x x 2 〔C 〕f (x )＝42-x ,g (x )＝22-+x x 〔D 〕f (x )＝|x ＋1|,g (x )＝⎩⎨⎧-<---≥+1111x x x x 7．假设奇函数f(x)在区间[3，7]上是增函数且最小值为5，那么f(x)在区间[－7，－3]上是〔〕 〔A 〕增函数且最大值为－5 〔B 〕增函数且最小值为－5≠⊂≠⊂〔C 〕减函数且最小值为－5 〔D 〕减函数且最大值为－58．)(x f 是偶函数,且当0>x 时,x x x f -=2)(,那么当0<x 时,)(x f 的解析式为〔〕〔A 〕x x x f -=2)(〔B 〕x x x f --=2)(〔C 〕x x x f +=2)(〔D 〕x x x f +-=2)(9．函数24)(2++=ax x x f 在)6,(-∞内递减，那么a 的取值范围是〔〕 〔A 〕3≥a 〔B 〕3≤a 〔C 〕3-≥a 〔D 〕3-≤a10．函数x y 111+=的定义域是〔〕〔A 〕0>x 〔B 〕0>x 或者1-≤x 〔C 〕0>x 或者1-<x 〔D 〕10<<x二．填空题〔每一小题5分，一共10分〕11．=A ｛23|≤≤-x x ｝，=B ｛1212|+≤≤-m x m x ｝，且BA ，那么实数m 的 取值范围为。

高一数学周周练（ 必修4综合）班级__________ 姓名_________ 学号______一、选择题: 本大题共10小题,每小题4分,共40分 1、若),1,3(),2,1(-==则=-2 （ ）A 、 )3,5(B 、 )1,5(C 、 )3,1(-D 、 )3,5(--2、5a b ==，a与b的夹角为3π，则a b -等于（ ）A ．35B ．235 C ．3 D ． 53．已知角α 的终边过点P （-4，3），则ααcos sin 2+的值为（ ） A ．54- B ．53C ．52D ．24、 已知函数f (x)sin(x )cos(x )=+ϕ++ϕ为奇函数，则ϕ的一个取值为（ ） A 、0 B 、2π C 、4π-D 、π5.设),6,2(),3,4(21--P P 且P 在21P P=,则点P 的坐标是 （ ）A 、)15,8(-B 、 (0,3)C 、)415,21(-D 、)23,1( 6．已知a=（4，3），向量b是垂直于a的单位向量，则b=（ ）A ．5354)54,53(，或（）B ．5354)54,53(，或（-- ）C ．5453)54,53(--，或（ ）D ． 5453)54,53(，或（--）7．a =1，b=2，c a b =+ ，且c ⊥a ，则向量a 与b 的夹角为（ ）A ．30°B ．60°C ．120°D ．150→→→→→→→→b a a b b a b a 的模与，则方向的投影为在，方向的投影为在是非零向量，与、设438的模之比值为（ ）A 、43 B 、34 C 、73 D 、749.函数44f (x)sin(x)sin(x)ππ=+-是（ ）A 、周期为2π的奇函数B 、周期为2π的偶函数C 、周期为π的奇函数D 、周期为π的偶函数10. 设两个向量22(2,cos )a λλα=+- 和(,sin ),2m b m α=+ 其中,,m λα为实数.若2,a b = 则mλ的取值范围是（ ）A .[6,1]-B .[4,8]C .(,1]-∞D .[1,6]-二、填空题：本大题共6小题，每小题4分，满分24分.11、已知113a (,2sin ),b (cos ,),a 322=α=α 且∥b ，则锐角α的值为 ；12、若|a |＝|b |＝1，a ⊥b ，且2a ＋3b 与k a －4b 也互相垂直，则k 的值为 ；13、函数y cos 2x 4cos x,x [,]32ππ=-∈-的值域是 ；14、若为则ABC AB BC AB ∆=+∙,02三角形；15将π2cos 36x y ⎛⎫=+ ⎪⎝⎭的图象按向量π24⎛⎫=-- ⎪⎝⎭，a平移，则平移后所得图象的解析式为 16、下列命题：①若c a cb b a =⋅=⋅，则 ②若a 与b 是共线向量，b 与c 是共线向量，则a 与c 是共线向-=+0=⋅ba ④若a 与b 是单位向量，则1=⋅其中真命题的序号为 。

2021年高一下学期周周练数学试题1一、填空题(每小题5分，共70分)1.已知集合,,24|,,22|⎭⎬⎫⎩⎨⎧∈+==⎭⎬⎫⎩⎨⎧∈+==Z k k x x B Z k k x x A ππππ则集合与的关系是 .2.如果与角终边相同，那么是第 象限角.3.设，角的终边经过点那么= .4. 已知扇形的周长是，圆心角为2rad ，则该扇形的面积为 .5.若点在角终边上，且满足，，则= .6. 已知角和的终边关于对称，且，则 .7.已知则 .8. 将表示为其中的形式是 .9. 已知集合，，则=.10.已知则 .11．.已知角的终边上一个点的坐标为，则的值为.12. 则= .13. 在扇形中，,弧长为，则扇形内切圆的面积为14．已知对一切实数恒成立，且则的值为 .二、解答题（共90分），写出详细的解答过程，作图题要保留作图痕迹.15.（本题满分14分）已知角终边上一点且，试求和的值.16. （本题满分14分）已知,其中为第三象限角,求的值.17. （本题满分14分）已知一扇形的周长是，当它的半径和圆心角取何值时，才能使扇形的面积最大？最大面积是多少？18.（本题满分16分）已知求下列各式的值.(1); (2).19.（本题满分16分）已知(1)求证：；(2)求的值.20. （本题满分16分）已知函数是定义在上周期为的偶函数，且.（1）求的值；（2）若时，求当时，的解析式.26503 6787 枇Me28736 7040 灀24186 5E7A 幺40622 9EAE 麮40707 9F03 鼃ah31777 7C21 簡34902 8856 衖21230 52EE 勮。