高一数学 周练答案 试题

高一上学期数学周练13一、选择题．请把答案直接填涂在答题卡相应位置上．．．．．．．．． 1.已知函数()f x 的定义域为[]-2,2，则函数()()3g x f x = （ D ）A ．2,13⎡⎤⎢⎥⎣⎦B ．[]1,1-C ．123,⎡⎤-⎢⎥⎣⎦D ．22,33⎡⎤-⎢⎥⎣⎦2．设⎭⎬⎫⎩⎨⎧-∈3,21,1,1α，则使函数αx y =的定义域为R 且为奇函数的所有的α的值为 （ A ）A.1，3B.-1，1C.-1，3D.-1，1，3 3．若幂函数()()22433m f x m m x -=--在()0,+∞上为减函数，则实数m =（ B ）A.41m m ==-或B.1m =-C. 21m m ==-或D. 4m =4．已知ba cb a ==⎪⎭⎫ ⎝⎛=,2.0log ,31312.0，则c b a 、、的大小关系为（ B ）A 、c b a <<B 、b a c <<C 、b c a <<D 、a c b <<5．已知函数()()log 4(0a f x ax a =->且1a ≠)在[]0,2上单调递减,则a 的取值范围是 （ B ） A ．()0,1 B ．()1,2 C ．()0,2 D ．[)2,+∞6．已知函数()()()()21,11log ,013aa x x f x x x ⎧->⎪=⎨-<≤⎪⎩，当1>0x ，20x >，且12x x ≠时，()()12120f x f x x x -<-，则实数a 的取值范围是 （ C ）A ．10,2⎛⎫ ⎪⎝⎭B ．11,32⎡⎫⎪⎢⎣⎭C ．10,3⎛⎤ ⎥⎝⎦D ．1,3⎛⎤-∞ ⎥⎝⎦ 7．函数()ln 1f x x =-的图象大致是 （ B ）A ．B ．C ．D ．8．已知函数()3122xxf x x =+-，若()()2120f a f a -+≤，则实数a 的取值范围为 （ D ）春雨教育A. (]1,1,2⎡⎫-∞-+∞⎪⎢⎣⎭B. 1,12⎡⎤-⎢⎥⎣⎦ C. [)1,1,2⎛⎤-∞-+∞ ⎥⎝⎦ D.11,2⎡⎤-⎢⎥⎣⎦二、多选题：（每小题给出的四个选项中，不止一项是符合题目要求的，请把正确的所有选项填涂在答题卡相应的位置上）9．（多选）下列各式比较大小，正确的是 （ BC ）A ．1.72.5＞1.73 B ．24331()22-> C ．1.70.3＞0.93.1D ．233423()()34>10．（多选）若,,()()(y)x y R f x y f x f ∀∈+=+有，则函数()f x 满足 （ ACD ）A． (0)0f = B．为偶函数()f x C．()f x 为奇函数 D．(2020)2020(1)f f = 11．（多选）下列说法正确的是 （ ABD ）A ．函数()24f x x x =-在区间()2,+?上单调递增B ．函数()24xxf x e -=在区间()2,+?上单调递增C ．函数()()2ln 4f x x x =-在区间()2,+?上单调递增D ．若函数()()1f x x ax =-在区间()0,+?上单调递增，则0a ≤12．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数“为：设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，例如：[ 3.5]4-=-，[2.1]2=．已知函数1()12=-+x xe f x e ，则关于函数()[()]g x f x =的叙述中正确的是 ( BC )A．()g x 是偶函数 B．()f x 是奇函数C．()f x 在R 上是增函数D．()g x 的值域是{}1,0,1-【解析】选BC ()()()111[012e g f e ==-=+，1111(1)[(1)][[]112121e g f e e-=-=-=-=-++，()()11g g ∴≠-，则()g x 不是偶函数，故A 错误； 1()12=-+x x e f x e 的定义域为R ， 111()()11121211xxx x x x x x e e e e f x f x e e e e---+=-+-=+-++++11011x x xe e e=+-=++，()f x ∴为奇函数，故B 正确； 111111()121221x x x xxe ef x e e e +-=-=-=-+++， 又x e 在R 上单调递增，11()21xf x e ∴=-+在R 上是增函数，故C 正确；春雨教育0x e > ，11x e ∴+>，则1011x e <<+，可得11112212x e -<-<+，即11()22f x -<<． ()[()]{1g x f x ∴=∈-，0}，故D 错误．故选BC.三、填空题．请把答案直接填写在答题卡相应位置上．．．．．．．．． 13．已知定义在R 上的奇函数，当0x <时有3()2x f x x =-+，则()f x =____332,00,02,0x x x x x x x -⎧+>⎪=⎨⎪-+<⎩_____14．若关于x 的函数12(log )x y a =是R 上的减函数，则实数a 的取值范围是1(,1)2． 15．设函数2()log )f x x =，若对任意的(1,)x ∈-+∞，不等式(ln )(24)0f x a f x -++<恒成立，则a 的取值范围是___(0,]e ____.16．设函数()()()2,142,1x a x f x x a x a x ⎧-<⎪=⎨--≥⎪⎩. ①若1a =，则()f x 的最小值为____1-___；②若()f x 恰有2个零点，则实数a 的取值范围是___[)1,12,2⎡⎫+∞⎪⎢⎣⎭____.四、解答题．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．17. 设函数()()⎪⎭⎫ ⎝⎛⋅=4log 8log 22x x x f ，144x ≤≤，(1)求⎪⎭⎫⎝⎛41f 的值(2)若2log t x =，求t 取值范围；(3)求()f x 的最值，并给出最值时对应的x 的值。

高一数学周末练习 2015-5-241.不等式2x x <的解集是2. 从1，2，3，4这四个数中一次随机取两个数，则其中一个数是另一个 的两倍的概率为 .3. 阅读右边的程序框图，运行相应的程序，则输出的值为 .4.在各项均为正数的等比数列{}n b 中，若783b b ⋅=， 则3132log log b b ++……314log b += .5. 数列{}n a 的前n 项和*23()n n S a n N =-∈，则=n a .6. 一支田径队有男运动员48人，女运动员36人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为 . 7.ABC ∆中，若a ，b ，c 成等差数列，30B =，ABC ∆的面积为23， 那么b =________.8.数列{}n a 满足12a =，112n n na a --=，则n a = . 9.已知31x y +=，则28x y +的最小值为____________.10.若ABC ∆的三个内角,,A B C 成等差数列，1AB =，4BC =，则边BC 上的中线AD 的长为 .11. 设y x ,为实数，若1422=++xy y x ，，则y x +2的最大值是 . 12.在ABC ∆中边,,a b c 成等比数列，则B 的取值范围是 . 13.若关于的不等式对任意的正实数恒成立，则实数的取值范围是 .14.ABC ∆中，D 在边BC 上，且2BD =，1DC =，60B ∠=，150ADC ∠=，则ABC ∆的面积为 .15. 在△ABC 中，设角A ，B ，C 的对边分别为a ，b ，c ，且．（1）求角A 的大小；（2）若，求边c 的大小．i x 2(20)lg 0aax x-≤x a 1cos 2a C cb +=a =4b =16.经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量y （千辆/小时）与汽车的平均速度v （千米/小时）之间的函数关系为：2920(0)31600vy v v v =>++． （1）在该时段内，当汽车的平均速度v 为多少时，车流量有何最大值？（保留分数形式） （2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？17.将n 2个数排成n 行n 列的一个数阵：111213121222323132333123n n n n n n nna a a a a a a a a a a a a a aa 已知a 11＝2，a 13＝a 61＋1．该数阵第一列的n 个数从上到下构成以m 为公差的等差数列，每一行的n 个数从左到右构成以m 为公比的等比数列，其中m 为正实数． （Ⅰ）求第i 行第j 列的数a ij ；（Ⅱ）求这n 2个数的和．参考答案：1、{|1x x >或0}x <.2、31. 3、4. 4、7. 5、123-⋅=n n a . 6、12. 7、1、51()22n -. 9、、. 12、(0,]3π. 14、解：在△ABC 中，∠BAD ＝150o －60o ＝90o ，∴AD ＝2sin60o＝3．在△ACD 中，AC 2＝(3)2＋12－2×3×1×cos150o ＝7，∴AC ＝7．∴AB ＝2cos60o ＝1．S △ABC ＝21×1×3×sin60o ＝343． 15（2）用余弦定理，得16、解：（Ⅰ）依题意，,83920160023920)1600(3920=+≤++=vv y 当且仅当1600v v =，即40v =时，max 92083y =（千辆/小时）（Ⅱ）由条件得,10160039202>++v v v整理得v 2－89v +1600<0, 即（v －25）（v －64）<0,解得25<v <64.答：当v =40千米/小时，车流量最大，最大车流量约为11.1千辆/小时.如果要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应大于25千米/小时且小于64千米/小时．2222cos .a b c bc A =+-17、解：（Ⅰ）由a 11＝2，a 13＝a 61＋1，得2m 2＝2＋5m ＋1．………2分解得m ＝3或m ＝12-（舍去）． ………………………………………4分11113[2(1)]3(31)3j j j ij i a a i m i ---=⋅=+-=-．…………………………7分（Ⅱ）S ＝111212122212()()()n n n n nn a a a a a a a a a ++++++++++＝11121(13)(13)(13)131313n n n n a a a ---+++---………………………………10分＝1(231)1(31)(31)(31)224n n n n n n +--⋅=+-．…………………………15分。

高一年级下学期数学周测试卷一、选择题（本题12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求）。

1、= 210sin A 23 ；B 23- ；C 21 ；D 21- 2、函数|sin |x y =的一个单调增区间是A 、)4,4(ππ-B 、)43,4(ππ C 、)23,(ππ D 、)2,23(ππ 3、不等式0412>--x x 的解集是 A 、（－2，1） B 、（2，+∞） C ),2()1,2(+∞- D ),1()2,(+∞--∞4、设集合}23{<<-∈=m Z m M ,}31{≤≤-∈=n Z n N ,则=⋂N M A ．}1,0{ B. }1,0,1{- C. }2,1,0{ D }2,1,0,1{-5、函数x xx f -=1)(的图像关于 A ． y 轴对称 B.直线y=-x C.坐标原点对称 D.直线y=x6、若动直线a x =与函数x x f sin )(=和x x g cos )(=的图像分别交于M 、N 两点，则MN 的最大值为（ ）A ．1 B. 2 C. 3 D.27、已知正四棱锥S-ABCD 的侧棱长与底面边长都相等，E 是SB 的中点，则AE 、SD 所成的角的余弦值为（ ）A ． 31 B. 32 C. 33 D. 32 8、要得到函数y ＝sin(4x －π3)的图像，只需将函数y ＝sin4x 的图像( ) A ．向左平移π12个单位 B ．向右平移π12个单位 C ．向左平移π3个单位 D ．向右平移π3个单位 9．a 、b 为非零向量，且|a ＋b |＝|a |＋|b |，则( )A ．a ∥b ，且a 与b 方向相同B ．a 、b 是方向相反的向量C ．a ＝－bD ．a 、b 无论什么关系均可10．某单位有老年人27人，中年人54人，青年人81人，为了调查他们的身体状况的某项指标，需从他们中间抽取一个容量为36的样本，则老年人、中年人、青年人分别应抽取的人数是（ ）A ．7，11，19B ．6，12，18C ．6，13，17D ．7，12，1711．把函数f (x )＝sin 2x ＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数g (x )的图象，则g (x )的最小正周期为( )A ．2πB ．Π C.π2D.π412．sin 120°cos 210°的值为( )A ．－34 B.34 C ．－32D.14 二、填空题（每小题5分，共20分）13．在△ABC 中，＝a ，＝b ，＝c ，则a ＋b ＋c ＝________. 14、1－tan 15°1＋tan 15°= 15、设f(x)是周期为2的奇函数，当0≤x ≤1时，f(x)=2x(1-x),则⎪⎭⎫ ⎝⎛-25f = 16、已知⎪⎭⎫ ⎝⎛∈ππα,2，55sin =α，则tan2α=_______________。

高一数学周考试题 参考答案一.选择题： 1-5：ABDAC6——10：BBADA 10.解：()f x =====令1sin 2cos x m x +=-，则1sin 2cos x m m x +=-，sin cos 21x m x m +=-)2n(1x m ϕ=+-得)sin(x ϕ=+1≤解得403m ≤≤，()f x =单增，值域为⎡⎢⎣11 .； 12. 1344a b +； 13. 20； 14. 1； 15.⎫⎪⎭. 15.解： 222221122(2),2,0()21211(1),,0x x x x x x x f x x x x x x x x -≤-----≤⎧⎧==⎨⎨->-----+>⎩⎩，绘出简图 若方程()f x m =有三个根，则104m <<，且当0x >时方程可化为20x x m -+-=，易知，231x x +=，23x x m =；当0x ≤时方程可化为220x x m --=，可解得1x = 记y=2222212312323()212x x x x x x x x m ++=++-=-3928m =-+令t =，则2312116816y t t =--+，求得y ⎫∈⎪⎭三.解答题.( 本大题共6小题,共75分.解答须写出文字说明、证明过程和演算步骤.)16. 解：(Ⅰ)令tan x α=，则132x x -=-，22320x x +-=，解得12x =或2x =-， 2παπ<<，tan 0α<，故tan 2α=-； （Ⅱ）3cos()cos()sin cos 2tan 1211cos sin()2παπααααπαα+--+==+=-+=-- 17. 解：(Ⅰ) 571510714,,(,3)885888d a b λλλλλλλλ⎛⎫⎛⎫=+=+-= ⎪ ⎪⎝⎭⎝⎭2||d λ=+=1±，(1,3)d =或(1,3)d =--(Ⅱ) (34,2),2(5,2)a kc k k b a +=++-=-，由题得(34)(5)(2)02k k ⨯+--⨯+=，解得1613k =- 18.解：(Ⅰ)当1a >时，21max min (),()f x a f x a -==，则2218a a a -==，解得2a =； 当01a <<时，12max min (),()f x a f x a -==，则1328a a a --==，解得12a =； (Ⅱ) 当1a >时，由前知2a =，不等式2log (22)log (1)a a a x x +<+即为222log (42)log (1)x x +<+224202421230x x x x x x +>>-⎧⎧⇔⇔⎨⎨+<+-->⎩⎩213x x >-⎧⇔⎨<->⎩或得解集为(2,1)(3,)--+∞.19. 解：（Ⅰ）当2ω=时，2()4sin(2)3g x x π=+2()4sin(2)4sin(2)6333g x x x ππππ-=-+=+ ()4sin(2)3p x x π=+，令23x k ππ+=，得62k x ππ=-+，中心为,0()62k k Z ππ⎛⎫-+∈ ⎪⎝⎭； （Ⅱ）2()4sin()(cos )3f x x x πωω=+-14sin ()cos cos 2x x x ωωω⎡=-⋅-+⎢⎣22sin cos x x x ωωω=-sin 2cos2)x x ωω=-+2sin(2)3x πω=--由题意，Tπ=，2,12ππωω∴== 令23t x π=-是x的增函数，则需2sin y t =-是t 的增函数 故222232k x k πππππ-≤-≤+，522266k x k ππππ-≤≤+，51212k x k ππππ-≤≤+ 函数()f x 的单增区间是5,()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. 20.解：(Ⅰ) 若()f x 是偶函数，则有()()f x f x -=恒成立，即：22log (41)log (41)x x mx mx -+-=++ 于是2222412log (41)log (41)log ()log (41)24x x xx x mx x -+=+-+=-+=- 即是22mx x =-对x R ∈恒成立，故1m =- (Ⅱ)当0m >时，2log (41)x y =+，在R 上单增，y mx =在R 上也单增所以2()log (41)x f x mx =++在R 上单增，且(0)1f = 则()242418(log )2log 41f x x m ++-=可化为()242418(log )2log 4(0)f x f x m ++-= 又()f x 单增，得242418(log )2log 40x x m ++-=，换底得2222log 48()2log 40log 4x x m -+-=即22242(log )2log 40x x m -+-=，令2log t x =，则3[0,]2t ∈，问题转换化为 242240t t m -+-=在3[0,]2t ∈有两解24224t t m⇔=-++ 令2224y t t =-++，29312()(0)222y t t =--+≤≤，max 19()22y y ==， 作出29312()(0)222y t t =--+≤≤与4y m =的简图知，4942m ≤<解得819m <≤ 又0m >，故819m <≤. 21.解：(Ⅰ)由[][]()()(2)(1)(1)1(1)(1)1f x f y f xy x y f x y y f y x +=--+=-+-+=--+ 令1,1m x n y =-=-，则,0m n >，且有(1)(1)(1)f m f n f mn +++=+对任意,0m n >均成立 令1m n ==即有(2)(2)(2)f f f +=，得(2)0f =；(Ⅱ)由(1)(1)(1)f m f n f mn +++=+有(1)(1)(1)f mn f n f m +-+=+，只需1m >就好 设211,1x mn x n =+=+，其中,0,1n m m >>，则21(1)0x x n m -=->，故21x x >则21()()(1)(1)(1)f x f x f mn f n f m -=+-+=+，1,12m m >+>所以(1)0f m +>， 即21()()0f x f x ->，21()()f x f x >，()f x 在(1,)+∞单调递增(Ⅲ)由(1)(1)(1)f m f n f mn +++=+令3m n ==，有(4)(4)(10)f f f +=，(10)2f = 令19,9m n ==，由1(91)(1)(911)099f f f ⋅+++==+，故10()29f =-，由奇偶性10()29f -=- 则()2f x <的解集是 10(,)(1,10)9-∞-于是问题等价于是否存在实数k 使10sin 2(4)(sin cos )9k k θθθ--++<-或1sin 2(4)(sin cos )10k k θθθ<--++<对任意的[0,]θπ∈恒成立令sin cos ,[t t θθ=+∈-，问题等价于210(4)19t k t k --+-<-或21(4)110t k t k <--+-<对[t ∈-恒成立令2()(4)1g t t k t k =--+-，则10()9g t <-对[t ∈-恒成立的必要条件是10(1)9109g g ⎧-<-⎪⎪⎨⎪<-⎪⎩即123091109k k ⎧-+<⎪⎪⎨⎪+++<⎪⎩得1391989k k ⎧<⎪⎪⎨⎪>+++⎪⎩，此时无解； 同理1()10g t <<恒成立的必要条件是1(1)10110g g <-<⎧⎪⎨<<⎪⎩，即124101(1110k k <-<⎧⎪⎨<-++<⎪⎩解得57218k k ⎧<<⎪⎨⎪--<<+⎩，得572k <<； 当572k <<时，2()(4)1g t t k t k =--+-的对称轴042k t -=33,42⎛⎫∈- ⎪⎝⎭， （1）当47k +≤<时，对称轴04322k t -⎫=∈⎪⎭，在区间[-的右侧 2()(4)1g t t k t k =--+-在[-单调递减，1()10g t <<恒成立1(1)10110g g <-<⎧⎪⇔⎨<<⎪⎩成立故47k +≤<时，1()10g t <<恒成立；（2）当542k <<+042k t -=34⎛∈- ⎝ ，2()(4)1g t t k t k =--+-在[-先减后增 1()10g t <<恒成立还需min 4()12k g t g -⎛⎫=> ⎪⎝⎭，即2(4)4(4)1142k k k k ----+-> 化简为212240k k -+<，2(6)12k -<，即6k -<-<，解得66k -<<+故有66542k k ⎧-<<+⎪⎨<<+⎪⎩解得64k -<<+；综上所述存在()67k ∈-，使()sin 2(4)(sin cos )2f k k θθθ--++<对任意的[0,]θπ∈恒成立.。

高一数学周练(15)一、选择题：（本题共12小题，每小题5分，共60分）1．tan390°的值等于（）A．B．C．﹣D．﹣2．已知M={0，1，2}，N={x|x=2a，a∈M}，则M∪N=（）A．{0}B．{0，1}C．{0，1，2}D．{0，1，2，4}3．设P是△ABC所在平面内的一点，，则（）A．P、A、C三点共线B．P、A、B三点共线C．P、B、C三点共线D．以上均不正确4．给出下列四个式子：①=x；②a3＞a2；③（log a3）2=2log a3；④log23＞log49．其中正确的有（）A．0 个B．1个C．2个D．3个5．如图，已知∠AOB=2弧度，点A1、A2、A3在OA上，点B1、B2、B3在OB上，其中每一条实线段和虚线段长度均为1个单位．一个动点M从点O出发，沿着实线段和以点O为圆心的实线圆弧匀速运动，速度为1单位/秒．则动点M到达A2处所需时间为（）秒．A．6B．8C．2+πD．2+3π6．下列四个函数中，在（0，+∞）上为增函数的是（）A．y=﹣1B．y=x2﹣3x C．y=﹣D．y=﹣|x|7．设f（x）=3x+3x﹣8，用二分法求方程3x+3x﹣8=0在x∈（1，3）内近似解的过程中取区间中点x0=2，那么下一个有根区间为（）A．（1，2）B．（2，3）C．（1，2）或（2，3）D．不能确定8．已知函数f （x ）=，若f （f （﹣1）=18，那么实数a 的值是（ ）A ．0B ．1C ．2D ．39．若，则sin2α的值为（ ）A ．B ．C ．D ．10．如图2-3-6所示，△ABC 中，若D ，E ，F 依次是AB 的四等分点，则以CB →＝e 1，CA →＝e 2为基底时，CF →＝________.A. 34e 1＋14e 2 B.C. D.11．已知函数f （x ）=Asin （wx +φ）（A ＞0，w ＞0，|φ|＜，x ∈R ）在一个周期内的图象如图所示．则y=f （x ）的图象可由函数y=cosx 的图象（纵坐标不变）（ ）A ．先把各点的横坐标缩短到原来的倍，再向左平移个单位B ．先把各点的横坐标缩短到原来的倍，再向右平移个单位C ．先把各点的横坐标伸长到原来的2倍，再向左平移个单位D ．先把各点的横坐标伸长到原来的2倍，再向右平移个单位12．设函数f （x ）为偶函数，且当x ≥0时，f （x ）=（）x ，又函数g （x ）=|xsinπx |，则函数h （x ）=f （x ）﹣g （x ）在[﹣，2]上的零点的个数为（ ）个． A ．3B ．4C ．5D ．6二、填空题（共4小题，每小题5分，满分20分）13．（5分）已知集合M={x |log 2（x ﹣3）≤0}，N={x |y=}，则集合M ∩N 为 ．14．（5分）函数的单调增区间为 ．15．（5分）甲、乙二人从A 地沿同一方向去B 地，途中都使用两种不同的速度v 1与v 2（v 1＜v 2）．甲前一半的路程使用速度v 1，后一半的路程使用速度v 2；乙前一半的时间使用速度v 1，后一半时间使用速度v 2．请在如图坐标系中画出关于甲、乙二人从A 地到达B 地的路程与时间的函数图象（其中横轴t 表示时间，纵轴s 表示路程，C 是AB 的中点，t 1是t 2的一半）．16．定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当]2,0[π∈x 时，x x f sin )(=，则)35(πf 的值是 ． 三.解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．（1）已知||=1，||=，若与的夹角为，求|﹣|．（2）已知=（﹣4，3），=（1，2），求（﹣3）•（2+）的值．18．已知角α的顶点在坐标原点，始边与x 轴的非负半轴重合，终边经过点P （﹣3，4）．（1）求sinα，cosα的值；（2）的值．19．已知函数)32sin(23π+-=x y ．（1）求函数的值域； （2）求函数取最小值时x 的集合； （3）当⎥⎦⎤⎢⎣⎡-∈3,3ππx 时，求函数的最大值．20．设函数f （x ）=log a x ，x （0＜a ＜1）． （1）比较f （sin1）与f （cosl ）的大小；（2）记函数f （x ）的反函数为g （x ），若a +kg （x ﹣1）≥0在x ∈[2，+∞）上恒成立，求k 的最小值．21．已知函数2()log (21)x f x =+（1）求证：函数()f x 在(,)-∞+∞内单调递增；（2）若关于x 的方程2log (21)()x m f x -=+在[1,2]上有解，求m 的取值范围。

高一数学“每周一练”系列试题及答案
1．某初级中学领导采用系统抽样方法，从该校预备年级全体800名学生中抽50名学生做牙
齿健康检查。

现将800名学生从1到800进行编号，求得间隔数k
800
50
=16
，即每16
人抽取一个人。

在1~16中随机抽取一个数，如果抽到的是7，则从33 ~ 48这16个数中应取的数是（）
A．40．B．39．C．38．D．37．
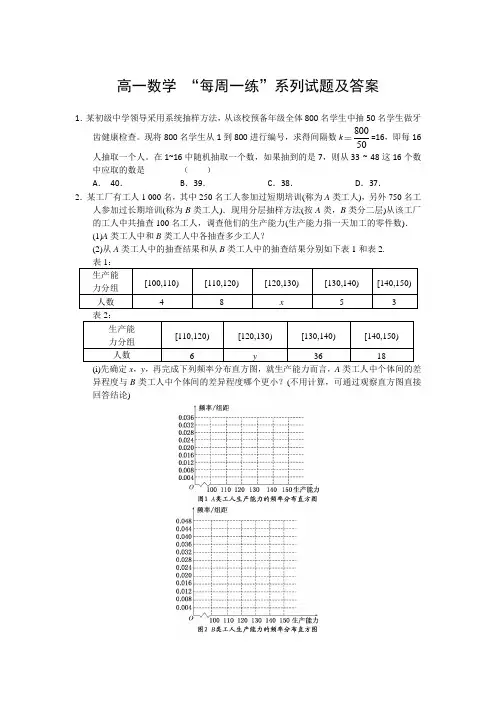
2．某工厂有工人1 000名，其中250名工人参加过短期培训(称为A类工人)，另外750名工人参加过长期培训(称为B类工人)．现用分层抽样方法(按A类，B类分二层)从该工厂的工人中共抽查100名工人，调查他们的生产能力(生产能力指一天加工的零件数)．
(1)A类工人中和B类工人中各抽查多少工人？
(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.
生产能
力分组
[100,110)[110,120)[120,130)[130,140)[140,150) 人数48x 5 3 生产能
力分组
[110,120)[120,130)[130,140)[140,150) 人数6y 3618
(i)先确定x，y，再完成下列频率分布直方图，就生产能力而言，A类工人中个体间的差
异程度与B类工人中个体间的差异程度哪个更小？(不用计算，可通过观察直方图直接回答结论)。

高一春季数学周测答案一．选择题1．下列命题中正确的是（ ）A ．终边和始边都相同的角一定相等B ．始边相同而终边不同的角一定不相等C ．小于90︒的角一定是锐角D ．大于或等于0︒且小于90︒的角一定是锐角 【答案】B2．下图终边在阴影部分的角的集合可表示为（ ）A ．{}18018030,k k k Z αα⋅<<⋅+∈B ．{}18018030,k k k Z αα⋅≤≤⋅+∈C ．{}36036030,k k k Z αα⋅<<⋅+∈D ．{}36036030,k k k Z αα⋅≤≤⋅+∈【答案】B3．一个半径是R 的扇形，其周长为3R ，则该扇形圆心角的弧度数为（ ）A ．1B ．3C ．πD ．3π 【答案】A4．下列两组角的终边不相同的是()k ∈Z （ ）A ．512k ππ+与712k ππ−+ B ．223k ππ−+与423k ππ+ C ．126k ππ+与1326k ππ+D ．14k ππ+与124k ππ±+【答案】D5．当α为第二象限角时，sin cos sin cos αααα−的值是（ ）． A ．1B ．0C ．2D ．2−【答案】C6．角α的终边上有一点P (a,a )，a ∈R ，且a ≠0，则sinα的值是（ ） A ．√22B ．−√22C ．±√22D ．1【答案】C 7．已知sinα−2cosθ3sinα+5cosα=−5,则tanα的值为( )A ．−2B ．2C ．2316 D ．−2316 【答案】D8． 已知函数()()2242,1,log 1,1,x x x f x x x ⎧++≤⎪=⎨−>⎪⎩，若关于x 的方程()f x t =有四个不同的实数解1x ，2x ，3x ，4x ，且1234x x x x <<<，则)1234122x x x x ++的最小值为（ ） A ．72 B ．8 C ．92D ．12 【答案】D【分析】先画出分段函数图像，确定1x ，2x ，3x ，4x 的范围，由()()3334log 1log 1x x −−=−结合对数运算可得()()34111x x −−=，)12x x 与34122x x +分别利用均值不等式求最小值，确认取等条件相同，即可得最小值.【详解】函数图像如图所示，()17f =，(]0,7t ∈，1234212x x x x <−<≤<<<，124x x +=−，由()()()()()()333433434log 1log 1log 110111x x x x x x −−=−⇒−−=⇒−−=， ∴()()34342112122251x x x x =−+++−5922≥=，当且仅当343,32x x ==时，等号成立，此时1t =；)()2212121212422x x x x x x x x ⎛⎫+⎛⎫=−≥−=−=− ⎪ ⎪ ⎪⎝⎭⎝⎭，当且仅当1222x x =−=−+1t =.所以)1234122x x x x ++的最小值为91422−=.9．终边在直线y =的角的集合为（ ）A ．{}0=60+360,k k Z αα−∈B ．{}0=60+180,k k Z αα−∈C ．{}=120+360,k k Z αα∈D ．{}=120+180,k k Z αα∈【答案】BD10．化简√1−sin 2160°的结果是( ) A ．cos160° B ．|cos160°| C ．±cos160° D ．cos20°【答案】BD11．下列各式中，值为1的是（ ） A ．122sin45−︒B ．4222sin sin cos cos αααα++C ．9tan π4D ．lg2lg5⨯【答案】ABC12．已知π1sin 33x ⎛⎫−= ⎪⎝⎭，且π02x <<，则以下结论正确的有( )A.π1sin 63x ⎛⎫+= ⎪⎝⎭B.πsin 6x ⎛⎫+ ⎪⎝⎭C.2π1cos 33x ⎛⎫+=− ⎪⎝⎭D.2πcos 3x ⎛⎫+= ⎪⎝⎭【答案】BD 二．填空题13.25cos 4π⎛⎫−= ⎪⎝⎭__________.【答案】√2214．已知:p “角α的终边在第一象限”，:q “sin 0α>”，则p 是q 的________ 条件（填“充分非必要”、“必要非充分”、“充要”或“既不充分也不必要”） 【答案】充分非必要”15.设()cos 24n f n ππ⎛⎫=+ ⎪⎝⎭，则(1)(2)(3)(2022)f f f f ++++=__________.【答案】-√216．已知()()222log 2log 24f x x t x t =−++，在1,164x ⎡⎤∈⎢⎥⎣⎦时，()f x 的最小值为()g t ，当关于t 的方程有()10g t t a −−+=有两个不等实根时，a 的取值范围是__________． 【答案】()5,−+∞【分析】换元[]2log 2,4s t =∈−，求出二次函数2224y s ts t =−++在[]2,4s ∈−上的最小值()g t 的表达式，然后作出函数y a =−与函数()1y g t t =−−的图象，利用数形结合思想可求出实数a 的取值范围.【详解】当1,164x ⎡⎤∈⎢⎥⎣⎦时，令[]2log 2,4s x =∈−，则()g t 为二次函数2224y s ts t =−++在[]2,4s ∈−上的最小值，该二次函数图象开口向上，对称轴为直线s t =.①当2t ≤−时，函数2224y s ts t =−++在区间[]2,4−上单调递增， 此时，()()()22222468g t t t t =−−⨯−++=+；②当24t −<<时，二次函数2224y s ts t =−++在s t =处取得最小值，即()224g t t t =−++；③当4t ≥时，二次函数2224y s ts t =−++在区间[]2,4−上单调递减，此时，()242424620g t t t t =−⨯++=−+.综上所述，()268,224,24620,4t t g t t t t t t +≤−⎧⎪=−++−<<⎨⎪−+≥⎩.由()10g t t a −−+=得()1a g t t −=−−，则函数y a =−与函数()1y g t t =−−的图象有两个交点，令()()2277,233,2115,14721,4t t t t t h t g t t t t t t t +≤−⎧⎪−++−<<⎪=−−=⎨−++≤<⎪⎪−+≥⎩，作出函数y a =−与函数()y h t =的图象如下图所示：如图所示，当5a −<时，即当5a >−时，函数y a =−与函数()y h t =的图象有两个交点，此时，关于t 的方程有()10g t t a −−+=有两个不等实根. 因此，实数a 的取值范围是()5,−+∞. 故答案为：()5,−+∞. 三．解答题 17. 【答案】 (1)3sin 5α=−(2)5418. 【答案】（1）17；（2）15−. 19. 【答案】（1）−√39；（2）√22.20．【答案】（1）函数()()233log a f x a a x =−+是对数函数，233101a a a a ⎧−+=⎪∴>⎨⎪≠⎩，解得2a =，()2log f x x ∴=，211log 122f ⎛⎫∴==− ⎪⎝⎭（2）()2log f x x =在定义域()0,∞+上单调递增，()121f f m m ⎛⎫∴>− ⎪⎝⎭可得到21010121m mm m⎧⎪−>⎪⎪>⎨⎪⎪>−⎪⎩，解得112m <<，∴不等式()121f f m m ⎛⎫>−⎪⎝⎭解集为1,12⎛⎫ ⎪⎝⎭．21． 【答案】（1）(,4][2,)−∞−+∞；（2）存在，91,4⎛−+− ⎝⎦． 【解析】（1）利用绝对值三角不等式求得()f x 的最小值，进而根据不等式恒成立的意义得到关于a 的含绝对值的不等式，求解即得；（2）根据a 和x 的范围化简得到含有参数a 的关于x 的一元二次不等式，利用二次函数的图象和性质，并根据不等式恒成立的意义得到关于实数a 的有关不等式（组），求解即得.【详解】解：（1）∵()|31||3|f x x x a =−++，的∴()|(31)(3)||1|f x x x a a ≥−−+=+， 当且仅当(31)(3)0x x a −+≤时，取等号． ∴原不等式等价于13a +≥， 解得2a ≥或4a ≤−．故a 的取值范围是(,4][2,)−∞−+∞． （2）∵1a >−，∴133a −<， ∵1,33a x ⎡⎤∈−⎢⎥⎣⎦，∴()|31||3|1f x x x a a =−++=+，()(1) g x a x =+，∴原不等式恒成立22(1)53(6)30a x x x x a x ⇔+≥−−⇔−+−≤在1,33a x ⎡⎤∈−⎢⎥⎣⎦上恒成立，令2()(6)3u x x a x =−+−，2423039a u a a ⎛⎫−=+−≤ ⎪⎝⎭得a ≤≤且14410393u a ⎛⎫=−−≤ ⎪⎝⎭，得443a ≥−，又1a >−，得914a −+−<≤．故实数a 的取值范围是91,4⎛−+− ⎝⎦．22．【答案】(1)略；(2)17,18⎡⎤−−⎢⎥⎣⎦；(3)1⎡⎣. 【分析】（1）根据“伪奇函数”的概念，可以求出1x =±满足()()f x f x −=−，得到()f x 是“伪奇函数”；（2）由幂函数的概念求出n 的值，把结论转化为对勾函数在1,44⎡⎤⎢⎥⎣⎦的值域问题，进而解不等式得答案；（3）由题意把结论化为关于22x x −+的二次方程有解的问题，通过换元引入二次函数，进而转化二次函数为在给定的区间有零点问题，列不等式解得答案.【详解】（1）若函数2()21f x x x =−−为“伪奇函数”，则方程()()f x f x −=−有实数解， 即222121x x x x +−=−++有解，整理得21x =解得1x =±，所以()f x 为“伪奇函数”； （2）因为3()(1)(R)n g x n x n −=−∈为幂函数，所以11n −=即2n =，所以()g x x =， 则由()2x f x m =+为定义在[2,2]−上的“伪奇函数”， 所以22x x m m −+=−−在[2,2]−有解，整理得122222x x x xm −−=+=+， 令2x t =，则144t ≤≤，对于函数()1h t t t=+， 设12144t t ≤<≤，则()()()212121211t t h t h t t t t t −−=−⋅ 当121,,14t t ⎡⎤∈⎢⎥⎣⎦时，有()()21h t h t <，所以()h t 是减函数，当[]12,1,4t t ∈时，有()()21h t h t >，所以()h t 是增函数， 又()111744444h h ⎛⎫==+= ⎪⎝⎭，()12h =，所以()1724h t ≤≤，所以17224m ≤−≤解得1718m −≤≤−，所以实数m 的取值范围是17,18⎡⎤−−⎢⎥⎣⎦；（3）若12()422x x f x m m +=−⋅+−是定义在R 上的“伪奇函数”，则()()f x f x −=−在R 上有实数解，即2242224222x x x x m m m m −−−⋅+−=−+⋅−+，整理得()244222240x x x x m m −−+−++−=，()()2222222260x x x x m m −−+−++−=，令122222x x x x s −=+=+≥=，当且仅当0x =取到等号， 则222260s ms m −+−=在[)2,+∞上有解，令()()22222266h s s ms m s m m =−+−=−+−在[)2,+∞上有零点，所以()222Δ44260m m m ≥⎧⎪⎨=−⨯−≥⎪⎩，即2m m ≥⎧⎪⎨≤≤⎪⎩2m ≤或者()()222222420Δ44260m h m m m m ⎧<⎪⎪=−−≤⎨⎪=−⨯−≥⎪⎩，即211m m m <⎧⎪≤≤+⎨⎪≤≤⎩12m <，综上可得m的取值范围是1⎡⎣。

高一数学周考试题及答案一、选择题（每题3分，共30分）1. 函数f(x)=x^2-6x+8的零点个数是（）。

A. 0B. 1C. 2D. 32. 已知函数f(x)=2^x，g(x)=x+1，则f[g(x)]等于（）。

A. 2^(x+1)B. 2^x + 1C. x^2 + 2x + 2D. 2^x + 2^(x+1)3. 若a，b∈R，且a>b，则下列不等式中一定成立的是（）。

A. a^2 > b^2C. 1/a < 1/bD. a/b > 14. 已知向量a=(3, -2)，b=(1, 2)，则向量a+2b的坐标为（）。

A. (5, 2)B. (5, -2)C. (1, -6)D. (1, 2)5. 已知集合A={x|x^2-5x+6=0}，则A的元素个数为（）。

A. 0B. 1C. 2D. 36. 若函数f(x)=x^3-3x，求f'(x)的值（）。

A. 3x^2-3C. x^2-3D. x^2+37. 已知等差数列{an}的首项a1=1，公差d=2，则a5的值为（）。

A. 9B. 10C. 11D. 128. 已知双曲线x^2/a^2 - y^2/b^2 = 1的焦点在x轴上，且a=2，b=1，则该双曲线的离心率为（）。

A. √3B. √5C. √6D. √79. 已知函数f(x)=|x|，求f(-2)的值为（）。

A. 2B. -2C. 0D. 410. 已知圆的方程为(x-2)^2 + (y+1)^2 = 9，求该圆的半径为（）。

A. 3B. 4C. 5D. 6二、填空题（每题4分，共20分）11. 已知函数f(x)=x^2-4x+3，求f(1)的值为______。

12. 若向量a=(2, 3)，b=(-1, 2)，则向量a·b的值为______。

13. 已知等比数列{bn}的首项b1=2，公比q=3，则b3的值为______。

14. 已知直线l的方程为y=2x+3，求该直线的斜率为______。