计算过程
- 格式:doc
- 大小:429.50 KB
- 文档页数:15

乘法的运算顺序乘法是数学中的基本运算之一,它在我们日常生活和学习中有着广泛的应用。
然而,在进行乘法运算时,有时候会出现疑惑,不知道该按照什么顺序进行计算。
本文将为大家介绍乘法的运算顺序,帮助读者正确理解和应用乘法。
1. 什么是乘法运算顺序?乘法运算顺序是指当一个式子中包含多个乘法运算时,应该按照什么顺序进行计算。
乘法运算按照先算乘法后算加减的原则,即乘法运算优先于加法和减法运算。
2. 乘法运算顺序的规则乘法运算顺序的规则可以简单记为“括号里面先,乘除后,加减最后”。
这是因为在数学中,乘法和除法的优先级高于加法和减法。
3. 示例一:简单乘法运算让我们通过一个简单的例子来说明乘法运算顺序。
假设我们有一个式子:3 × 5 + 2根据乘法运算顺序,我们先进行乘法运算,再进行加法运算。
所以计算过程如下:3 × 5 + 2 = 15 + 2 = 17因此,结果为17。
4. 示例二:带有括号的复杂乘法运算有时候,乘法运算会与其他运算符(如括号)一起出现。
让我们看一个带有括号的复杂乘法运算的例子:(4 + 3) × 2根据乘法运算顺序规则,“括号里面先”。
所以我们先计算括号内的加法运算,得到:(4 + 3) × 2 = 7 × 2然后我们进行乘法运算,得到结果:7 × 2 = 14因此,结果为14。
5. 示例三:多个乘法运算的运算顺序当一个式子中包含多个乘法运算时,我们需要按照从左往右的顺序进行计算。
让我们看一个例子:3 × 2 × 4根据乘法运算顺序,我们先计算3 × 2,得到6。
然后再将6与4相乘,得到最终结果:3 × 2 ×4 = 6 × 4 = 24因此,结果为24。
6. 结论在数学中,乘法运算顺序是根据乘法的优先性来确定的。
乘法运算优先于加法和减法运算,且在乘法运算中,我们按照“括号里面先,乘除后,加减最后”的规则进行计算。

等额本息计算公式的推导过程
等额本息是一种常见的贷款还款方式,也是银行和金融机构常用的一种计算公式。
它的推导过程可以从以下几个步骤进行描述。
假设某人向银行贷款一笔金额为X的钱,期限为n个月,月利率为r。
根据等额本息的定义,每个月需要偿还的本息金额是固定的。
我们将每个月的还款额设为P。
根据贷款金额、期限和月利率,我们可以得到每个月的利息和本金的具体数值。
第一个月的利息为贷款金额X乘以月利率r,第一个月的本金为还款额P减去利息。
以此类推,第二个月的利息为剩余本金乘以月利率r,第二个月的本金为还款额P减去利息,依此类推。
然后,我们可以将贷款金额、利息和本金的计算过程用数学公式总结起来。
每个月的利息可以表示为X乘以r,每个月的本金可以表示为P减去利息。
根据等额本息的定义,每个月的还款额P应满足下面的等式:X乘以r加上(P减去(X乘以r))等于P。
我们通过求解上述等式,可以得到还款额P的具体数值。
根据上述推导过程,我们可以得到等额本息的计算公式:P等于X乘以r乘以(1加上r的n次方)除以(1加上r的n次方减去1)。
通过这个公式,我们可以计算出每个月的还款额P,并按照这个数值进行还款。
每个月还款额相同,由于每个月的利息递减,所以每
个月还款的本金会逐渐增加。
最终,在n个月的还款期限内,我们可以完成等额本息的贷款还款。
通过以上推导过程,我们可以看出等额本息的计算公式是如何得出的,并且明白了每个月还款额的变化规律。
这个计算公式在实际贷款中经常被使用,帮助借款人合理规划还款计划,同时也方便了银行和金融机构的贷款管理。
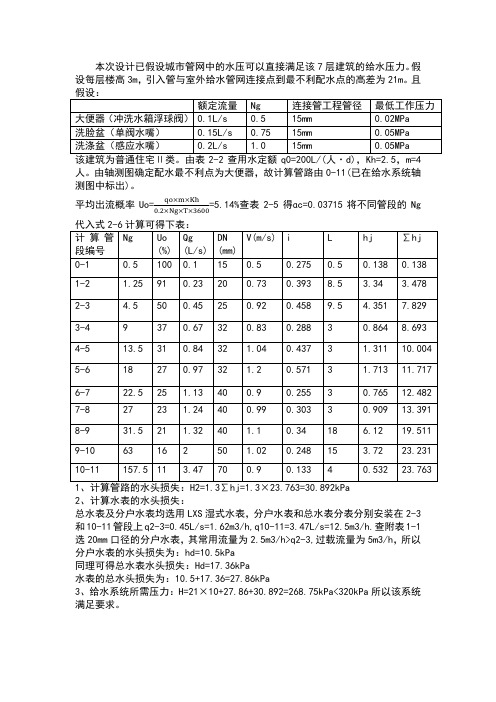
本次设计已假设城市管网中的水压可以直接满足该7层建筑的给水压力。
假设每层楼高3m,引入管与室外给水管网连接点到最不利配水点的高差为21m。
且
人。
由轴测图确定配水最不利点为大便器,故计算管路由0-11(已在给水系统轴测图中标出)。
=5.14%查表2-5得ɑc=0.03715将不同管段的Ng 平均出流概率Uo=qo×m×Kh
0.2×Ng×T×3600
2、计算水表的水头损失:
总水表及分户水表均选用LXS湿式水表,分户水表和总水表分表分别安装在2-3和10-11管段上q2-3=0.45L/s=1.62m3/h,q10-11=3.47L/s=12.5m3/h.查附表1-1选20mm口径的分户水表,其常用流量为2.5m3/h>q2-3,过载流量为5m3/h,所以分户水表的水头损失为:hd=10.5kPa
同理可得总水表水头损失:Hd=17.36kPa
水表的总水头损失为:10.5+17.36=27.86kPa
3、给水系统所需压力:H=21×10+27.86+30.892=268.75kPa<320kPa所以该系统满足要求。

2X2-2X+3M-1=0的两个实数根X1,X2,且X1&MIDDOT;X2》X1+X2-4,则21、(2005天津)若关于x的一元二次方程2x,2x,3m,1,0的两个实数根x,x,且x?x1212,x,x,4,则实数m的取值范围是 D 1251,(A)m, (B) m? 32551,,(C) m, (D) ,m? 332xy,,7,,2、(2005天津)解方程组 ,xy,12.,2x、x3、已知是一元二次方程的两个实根。
2x,2x,m,1,012(1)求实数的取值范围; m22(2)如果满足不等式,且为整数。
求的值。
7,4xx,x,xmmm121224、(淄博市2004).若关于x的一元二次方程有实数根,则k的取值范kx,2x,1,0围是(,)k,,1 (,)k?,1(,)k,,1且k?0 (,)k?,1且k?02x5、,2004年湖北省襄樊,已知关于的方程有两个实数mxmxm,,,,2(1)0根.m,1, 求的取值范围,,2, 若方程的两个实数根的平方和为6~求m的值.6、,2004年湖北省襄樊,汉江上游的某一牧场有162公顷~为了改善流域环境~把一部分牧场改为林场~改造后牧场面积是林场面积的20%~则退牧还林后~林场面积为____公顷.22,xyx,,,,210,7、,2004年湖北省襄樊,二元二次方程组的解是______. ,xy,,20,628、(遂宁市2004)解方程:( ,x—x,12x—x29、(遂宁市2004)已知关于x的一元二次方程 x,,2k—1,x—k—1,0(1) 试判断此一元二次方程根的存在情况;11x和x(2) 若方程有两个实数根,且满足,求k的值( ,,112xx1210、(泰州2004)四边形ABCD中,AB?CD,且AB、CD长是关于x的方程22的两个实数根,则四边形ABCD是 x,3mx,2m,m,2,0A. 矩形B. 平行四边形C. 梯形D. 平行四边形或梯形11、(泰州2004)用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt?BCE 就是拼成的一个图形.EM D M A AB BC C 图1 图2 图3 图4(1)用这两部分纸片除了可以拼成图2中的Rt?BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.(2)若利用这两部分纸片拼成的Rt?BCE是等腰直角三角形,设原矩形纸片中的边AB和2BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程x,(m,1)x,m,1,0的两个实数根,试求出原矩形纸片的面积.? S,ab,m,1,8矩形1x,1,12、(安徽理科实验班2004)若是方程的根,则的值为 mx,2m,2,0x,mm 【】A(0 B(1 C(,1 D(213、(安徽理科实验班2004)设为正整数,若是完全平方数,则它前面的一个完全x,1x平方数是【】A( B( C( D( xx,2x,1x,2x,1,1x,2x,1,2※※※14、(安徽理科实验班2004)甲、乙两个粮库原来各存有整袋的粮食,如果从甲库调90袋到乙库,则乙库存粮是甲库的2倍;如果从乙库调若干袋到甲库,则甲库存粮是乙库的6倍(问甲库原来最少存粮多少袋,答:甲库原来最少存粮153袋(215、(2004年苏州)已知关于x的一元二次方程 ax+x—a=0 ( a?0 )(1) 求证:对于任意非零实数a,该方程恒有两个异号的实数根;(2) 设x、 x是该方程的两个根,若?x?+ ?x?=4,求a的值。

简述mapreduce计算的主要流程
MapReduce计算是一种分布式计算模型,其主要流程可以简述为以下几个步骤:
1. 输入分片:将输入数据分成若干个小块进行处理,每个小块称为一个输入分片。
2. Map阶段:将每个输入分片分配给一个或多个Map任务进行处理。
每个Map任务读取一个输入分片,并将其转换为一系列<key, value>对。
这些<key, value>对称为Map输出。
3. Shuffle阶段:将Map输出按照key值进行排序,将具有相同key值的<key, value>对分组在一起,并将它们发送给同一个Reduce任务进行处理。
这个过程称为shuffle。
4. Reduce阶段:将每个Reduce任务处理的<key, value>对按照一定的规则进行合并(如求和、求平均值等),并输出结果。
5. 输出合并:将所有Reduce任务的输出结果合并成一个最终的输出结果,并将其存储到输出文件中。
以上就是MapReduce计算的主要流程,其中Map阶段、Shuffle 阶段和Reduce阶段是整个计算过程中最关键的三个阶段,它们的正确性和效率对整个计算的性能影响非常大。
- 1 -。

化学方程式计算的一般方法步骤
化学方程式计算的一般方法步骤如下:
1. 确定实验条件:确定实验所涉及的物质及其量,确定反应条件(如温度、压力等)。
2. 解析化学方程式:分解出反应物和生成物的化学式,并根据反应物的质量比例写出
反应式。
3. 计算物质的量:根据反应物的质量或体积,利用摩尔质量或气体摩尔体积计算物质
的摩尔数。
4. 确定摩尔比例:根据化学方程式中的系数,确定反应物之间的摩尔比例。
5. 计算所需量:根据摩尔比例,确定所需的反应物的摩尔数。
6. 计算生成物的量:根据化学方程式中的系数,确定生成物的摩尔数。
7. 计算生成物的质量或体积:根据生成物的摩尔数,利用摩尔质量或气体摩尔体积计
算生成物的质量或体积。
8. 检查答案:检查计算结果是否符合实验条件和化学方程式。
需要注意的是,化学方程式计算需要遵循质量守恒和摩尔守恒的原则,同时考虑到温度、压力等影响因素。
在计算过程中,还需要将化学式转化为摩尔数来进行计算。
另外,要注意反应的实际情况和理论情况可能存在偏差,因此计算结果仅为理论参考值。
顺序分配法计算步骤嘿,小伙伴们!今天咱们来唠唠顺序分配法的计算步骤,这就像是一场有趣的数字接力赛呢!首先啊,你得找到那个先起跑的“数字选手”,这就好比在一群小动物里找到最勇敢的那只小老鼠先出洞一样。
这个最先起跑的就是受益少、分配出去费用少的辅助生产车间啦。
把它的费用按照一定的规则分配给其他车间和部门,就像是小老鼠把自己的小坚果分给其他小伙伴一样,这个过程得仔仔细细地算哦,不然就乱套啦。
然后呢,第一个车间分配完了,就轮到下一个啦。
这个下一个车间就像是在小老鼠后面跑出来的小兔子。
它现在可就有点特殊了,因为它之前收到了小老鼠给的“小坚果”,也就是费用,所以它自己本身的费用再加上收到的那些,就像小兔子本来自己有胡萝卜,又收到了小坚果,现在它要带着这些一起分配给其他地方啦。
在计算这个“小兔子车间”分配的时候,那可不能马虎。
它就像一个背着重重包裹的快递员,要把包裹准确地送到各个收件人手里。
这里的收件人就是其他车间和部门啦。
计算它分配出去的比例和数额,就像快递员要按照地址精准投递一样。
接着呢,一个一个车间这样接力下去。
每一个车间都像是一个接力选手,带着前面选手交过来的“接力棒”,也就是费用,然后再加上自己的那部分,去传给下一个。
这个过程就像是一场滑稽的数字大游行,每个数字都有自己的任务和位置。
如果中间算错了一步呢?那就像是搭积木的时候抽错了一块,整个大楼就会摇摇欲坠啦。
所以每一步都要小心谨慎,就像走在钢丝上的杂技演员一样。
而且啊,这个顺序可不能乱,要是乱了就像是一群小动物排队去领食物,结果顺序乱了,大家就会挤成一团,谁也吃不到啦。
在整个计算过程中,那些数据就像是一群调皮的小猴子,你得好好抓住它们,让它们按照顺序分配法的规则乖乖听话。
要是哪个小猴子乱跑了,那算出的结果肯定是错得一塌糊涂,就像把盐当成糖放进蛋糕里一样,完全不是那么回事儿啦。
最后呢,当所有的车间都完成了自己的接力任务,这场顺序分配法的大狂欢就结束啦。
二年级数学简算,并写出主要过程例1:计算:96+15解:96+15 =96+(4+11)=(96+4)+11=100+11=111解析:把15分拆成15=4+11,这是因为96+4=100,可凑整先算。
这样拆分后再凑百,计算时就会比原先的算式计算起来更加简便,正确率也更高。
例2 :计算:52+69解:52+69 =(21+31)+69=21+100=121解析:观察题目,有一个特殊的数字69,因为69+31=100,所以把52分拆成21与31之和,再把31+69=100凑整先算。
例3:计算: 76+96解:76+96 =76+100-4=176-4=172解析:观察题目,这是两个数相加减的题目,其中一个数接近整百数,所以计算时,我们可以将96看作整百来计算,然后根据“多加要减,少加要加,多减要加,少减还要减”的原则来计算,这样计算时就会简便的多。
例4:计算231-102解:231-102=231-100-2=131-2=129解析:观察题目中的算式,减去102,我们先让它变成减去100,因为还少减了2,所以我们再减去2,就是最后的得数。
三个数的简便运算例1:计算:24+44+56解:24+44+56=24+(44+56)=24+100=124解析:先观察题目中的数,有没有能够凑成整百或者整十的,通过观察我们可以发现44和56可以凑成整百。
所以先计算44+56,再和第三个数相加。
这样计算是不是又快又准确呢?例2:计算:53+36+47解:53+47+36= ( 53+47)+36=100+36=136解析:观察题目。
先寻找有没有能够凑成整百的数。
因为53+47是能够凑成整百的数,所以先把+47带着符号搬家,搬到+36前面,然后再把53+47的和算出来。
算出来凑成整百以后当然就只需用一百加上第三个数36就可以得出结果136即可。
例3:计算124-26-74解:124-26-74 =124-(26+74)=124-100=24解析:观察算式,我们发现,连续减去两次,也就是减去两个数的总和,而且26和74的总和正好可以凑成整百,所以我们就直接用第一个数124减去后两个数总和就是最后的正确答案。
计算过程释义
计算过程是指进行数学运算或逻辑推理时所采取的一系列步
骤或方法。
计算过程可以涉及算术运算、代数运算、几何推理、逻辑推理等各种数学操作,也可以涉及到数据处理、图像处理、信号处理等实际应用中的算法和方法。
计算过程的释义可以从以下几个方面来理解:
1.数学运算过程:数学运算过程是指进行基本算术运算(如
加减乘除)、代数运算(如多项式的合并、因式分解)、几何
推理(如图形的构造、证明)、逻辑推理(如命题关系的判断、论证过程的推导)等数学操作时所采取的一系列方法和步骤。
在数学教育中,教师通常会教授学生们如何进行正确的计算过程,以使他们能够准确地得出正确的结果。
2.算法和方法:计算过程也可以指在实际应用领域中的算法
和方法。
例如,在计算机科学中,计算过程通常是指通过算法
来解决问题的方法,如排序算法、搜索算法、机器学习算法等。
在数据处理、图像处理、信号处理等领域,计算过程是指通过
一系列的数据操作和数学运算来处理数据和信号,以达到特定
的目的。
3.计算思维和推理能力:计算过程也可以理解为一种思维方
式和能力,即通过分析和推理来解决问题的能力。
计算思维强
调逻辑思维、问题分解、抽象建模、算法设计等能力,通过运
用这些能力来解决各种问题,不仅包括数学问题,还包括生活中的实际问题和工作中的挑战。
总之,计算过程是指进行数学运算或逻辑推理时所采取的一系列步骤或方法,它可以涉及数学运算、算法和方法,也可以涉及计算思维和推理能力。
计算过程在学习和实际应用中具有重要的作用,可以帮助我们解决各种问题并提高问题解决的效率和准确性。
单梁试验计算步骤计算基本过程:1、确定荷载,包括汽车、人群、二期等;2、在迈达斯中输入要计算的单梁截面尺寸;3、在桥梁博士中计算横向影响线坐标,然后按照坐标绘制横向影响线;4、查找规范,选择车道数目,在横向影响线上布载,人群按照线荷载布置在人行道的中心,求出移动荷载和人群荷载的横向分布系数;5、在迈达斯中建立单梁模型(若为连续梁,则建立单梁连续模型);6、求出移动荷载下单个车道的最大弯矩值(此处要考虑冲击系数)和单侧人群荷载作用下的弯矩值;7、求出二期荷载的总和,按照线荷载平均分配到每一片梁;8、将每一片梁分配的弯矩之和求出,不同截面尺寸的单梁各选一个最大弯矩值作为求加载效率的分母;9、迈达斯建立最大弯矩所在单梁的简支模型,在跨中进行加载试算,直到求出满足加载效率的加载值;9、查找控制截面的挠度和应变测点的应力值。
下面介绍某桥单梁试验的具体计算过程:一、确定荷载,包括汽车、人群、二期等;1)设计荷载:公路—Ⅱ级,人群荷载:3.0KN/m2;2)二期:60KN/m(图纸上如果没有二期的荷载,则需根据图纸材料表计算)3)桥梁宽度:净9m+2×4m(人行道+防护栏);二、在迈达斯中输入要计算的单梁截面尺寸;若截面为不对称截面,则应该在CAD中按照图纸绘出该截面,然后在迈达斯中使用截面特性值计算器,具体操作步骤可观看迈达斯教学视频中关于截面特性值计算器的内容,应该注意的是单位必须一致,CAD中使用的是什么单位,在截面特性值计算器中也必须选择该单位。
三、绘制横向影响线;在绘制横向影响线之前,首先查看桥梁图纸中单梁间的连接方式,一般有铰接(常用于空心板)、湿接缝(用于小箱梁、T梁)。
打开桥梁博士软件,选择新建,选择横向分布文件,如下图点确定之后进入下一窗口,选择刚接板梁法:然后按下结构描述按钮,如下图首先将填主梁跨度、G/E,然后输入主梁宽度,注意如果主梁间是湿接缝连接,主梁的宽度还应包括湿接缝。
一、卷帘机构的运动和受力分析1. 建立卷筒中心运动方程⑴求任一时刻卷筒与屋面切点P 的坐标 ①圆弧段O →A 令OC=e ,()θe =t S则⎪⎪⎭⎫⎝⎛+=22041t t r e πδωωθ切点P 在某时刻的坐标为:⎩⎨⎧++=+-=)sin()cos(11θθθθe y y e x x c p c p ②直线段A →B AB 直接:442.0665.2===αtg k︒=24αAC 直线:262.2442.011-=-=-=kk ACb x k y AC +=将A (1,1)代入→ -2.262+b=1 → b=3.262 AC 直线:262.3262.2+-=x y262.3262.2+-=c c x y ①()CA y x y x CO c c c c =-+-=+=22221)1(01=--∴c c y x ②联立方程组①、②,可得79.0,79.1-==c c y x C(1.79,-0.79) 279.079.122=+=e()56.65.12e 43246767279.0cos 2479.179.018043180431111==⨯==∴=︒=︒-︒=∴︒=+⇒=+︒=⇒=AB mOA tg πθπθθθθθθθ弧长P 点坐标:⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛++-=⎪⎪⎭⎫⎝⎛++-=απδωωααπδωωαsin 4sin 5.11cos 4cos 5.11220220t t r y t t r x p p ⑵卷筒中心运动方程①圆弧段O →A()()⎩⎨⎧+++=++-=)sin()()cos()(11θθθθt R e y y t R e x x c c ②直线度A →B()()⎪⎪⎩⎪⎪⎨⎧+⎪⎪⎭⎫ ⎝⎛++-=-⎪⎪⎭⎫⎝⎛++-=ααπδωωαααπδωωαcos sin 4sin 5.11sin cos 4cos 5.11220220t R t t r y t R t t r x2.任一时刻卷筒中心的速度和加速度 ⑴圆弧段O →A)()[]()()()[]()⎪⎩⎪⎨⎧++++'='++++'-='dt d t R e t R y dt d t R e t R x θθθθθθθθθθ1111cos sin )(sin cos )(()()2222)(⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++'='+'=dt d t R e t R y x v θ由于R ˊ(t)为小量,可略去 又()ωθt R e dtd 1=则()()ωt R e t R v ⎥⎦⎤⎢⎣⎡+=1 ()()()()()()⎪⎩⎪⎨⎧+-+'=''+++'=''dt d t R t R y dt d t R t R x θθθωθθωθθθωθθω1111sin cos )(cos sin )( ()()()()()et R dt d t R t R y x a 22222ωθωω≈⎪⎭⎫ ⎝⎛+'=''+''=⑵直线段A →B()()⎩⎨⎧'+=''-='ααωααωcos sin )(sin cos )(t R t R y t R t R x ()ωt R y x v ≈'+'=22⎩⎨⎧'='''=''αωαωsin )(cos )(t R y t R x ()πδωω2222='=''+''=t R y x a⑶求最大速度和加速度B 点处为最大速度,R(t)是越来越大mr 03.0min /6==δπω总的展开长度 m AB S 85.1=+=()()min8.28403.066025.022=⇒=⨯+⨯=t tt t S πππm t w r R B 295.03203.06025.020=⨯⨯+=+=πππδ()s mm s m m t R v B /7.92/0927.0min /561.56295.0max ===⨯==πω()224222/471.0/10712.4min/696.1203.062s mm sm m a =⨯==⨯==-πππδω化纤保温被在整个卷动过程中速度和加速度都很小,惯性作用不大。
3.受力分析电机质量 m=25kg 卷帘机质量 m=50kg 卷轴 m=300kg保温被加雪的重量 m=714+945=1659kg M 总=2034kg惯性力Fg=ma=2034×0.0004712=0.958N (方向与a 相反) 因为а不变,所以惯性力矩=J а=0MN T T R mg T ⋅==⨯⨯⨯-=-23520295.056.665.28.920340sin α二、传动比Z Z Z Z i 314231mZ Z i n 7.46631400n--====减总通过试凑法取:401=Z ,372=Z ;383=Z ,414=Z 估计 67.506i 1=H 查表得 mm m 3=三、内齿轮副的几何计算: 内齿轮 401=Z 外齿轮 372=Z ︒=20α齿顶高系数75.0=*a h 初选外齿轮变位系数:12=x 初选啮合角︒='31α0598086.0180/3131tan 3118506.11)2031(20tan 23740)(tan 22211=-︒=︒=+︒-︒︒-=+-'-=παααinv inv inv xinv inv Z x Z0149044.0180/2020tan 20=-︒=︒πinv标准中心距5.42)3740(32)(21=-⨯=-=Z Z m a实际中心距933.431cos 20cos 5.4cos cos =︒︒⨯='='ααa a啮合角α':︒='︒⨯='='9953.30933.420cos 5.4cos cos αααa a分离系数:144.035.4933.4=-=-'=ma a y反变位系数:041.0144.0118506.121=--=--=y x x σ分度圆直径:mm mZ r 602403211=⨯==mm mZ r 5.552373222=⨯==基圆半径: mm r r b 382.5620cos 60cos 11=︒⨯==αmm r r b 153.5220cos 5.55cos 22=︒⨯==α齿顶圆半径:mm m x h Z r a a 182.613)041.018506.175.0240()2(111=⨯-+-=-+-=*σmmm x h Z r a a 75.603)175.0237()2(222=⨯++=++=*齿顶压力角 921546.0182.61382.56cos 111===a b a r r α︒=85.221a α 858486.075.60153.52cos 222===a b a r r α︒=85.302a α 0588690.085.300225808.085.22=︒=︒inv inv()[]()[]1122.185.22tan 4085.30tan 379953.30tan 374021tan tan tan 21112221>=︒-︒+︒-=-+'-=παααπεα 重合度:a a Z Z Z Z外齿轮 383=Z 内齿轮 414=Z︒=20α齿顶高系数75.0=*a h 初选外齿轮变位系数:13=x 初选啮合角︒='31α0598086.0180/3131tan 3118506.11)2031(20tan 23841)(tan 23344=-︒=︒=+︒-︒︒-=+-'-=παααinv inv inv xinv inv Z x Z0149044.0180/2020tan 20=-︒=︒πinv标准中心距5.42)3841(32)(34=-⨯=-=Z Z m a实际中心距933.431cos 20cos 5.4cos cos =︒︒⨯='='ααa a啮合角α':︒='︒⨯='='9953.30933.420cos 5.4cos cos αααa a分离系数:144.035.4933.4=-=-'=ma a y反变位系数:041.0144.0118506.134=--=--=y x x σ分度圆直径:mm mZ r 572383233=⨯==mm mZ r 5.612413244=⨯==基圆半径: mm r r b 562.5320cos 57cos 33=︒⨯==αmm r r b 791.5720cos 5.61cos 44=︒⨯==α齿顶圆半径:mm m x h Z r a a 25.623)175.0238()2(333=⨯++=++=*mmm x h Z r a a 68.623)041.018506.175.0241()2(444=⨯-+-=-+-=*σ齿顶压力角 860433.025.62562.53cos 333===a b a r r α︒=63.303a α 922001.068.62791.57cos 444===a b a r r α︒=78.224a α 022365.078.22057511.063.30=︒=︒inv inv()[]()[]1127.178.22tan 4163.30tan 389953.30tan384121tan tan tan 21443334>=︒-︒+︒-=-+'-=παααπεα 重合度:a a Z Z Z Z四、一对内齿轮副的干涉及一些参数的限制 ⎩⎨⎧==374021Z Z (一)、内齿轮的齿顶圆不小于基圆 401320cos 1)041.018506.175.0(2cos 1)2382.56182.611111=<-=︒-+-⨯=-+-=>=*Z x h mm r mm r a b a ασ(又∴该内齿轮满足要求(二)、外齿轮的齿顶不得变尖,要有足够的厚度4.0~25.074.0)2085.30(3720tan 12285.30cos 20cos )(tan 22cos cos s 22222a >=⎥⎦⎤⎢⎣⎡︒-︒⨯-︒⨯⨯+︒︒=⎥⎦⎤⎢⎣⎡--+=inv inv inv inv Z x ma a παααπαα齿顶厚系数查图4-1也可知,变位系数未超过图中曲线,能保证足够的齿顶厚。
(三)、内齿轮的齿顶不得变尖,要有足够的厚度4.0~25.004.1)2085.22(4020tan 18506.12285.22cos 20cos )(tan 22cos cos s 11111a >=⎥⎦⎤⎢⎣⎡︒-︒⨯+︒⨯⨯-︒︒=⎥⎦⎤⎢⎣⎡-+-=inv inv inv inv Z x ma a παααπαα齿顶厚系数∴内齿轮的齿顶有足够的厚度(四)、过渡曲线的干涉 1、外齿轮的过渡曲线干涉 外齿轮用齿条刀切制21.219953.30sin 933.4382.56182.61sin 2221212=︒⨯--=''--=αρa r r b a∵ 外齿轮用正常齿高的齿条刀加工 ∴00=*a h98.1820sin 3)11(20sin 5.55sin )(sin 20202=︒⨯--︒⨯=--=*ααρmx h r a022ρρ>即由于,所以不会发生外齿轮的过渡曲线干涉2、内齿轮的过渡曲线干涉 内齿轮用插齿刀切制 ①选取内齿轮的插齿刀a. 确定不发生切入顶切所要求的插齿刀齿数查表4-11,在m=3、实际的齿顶高系数为8.0791.0041.075.0==+=+*σa h 、1x 1=、401=Z 时,可查得插齿刀的齿数及相应的最大变位系数为:b. 参考表4-3初步确定插齿刀的最小变位系数min 01x当插齿刀齿数3001≤Z ,取263.0min 01-=x 当插齿刀齿数3001>Z ,取315.0min 01-=xC.确定内齿轮不发生渐开线干涉顶切所要求插齿刀的最少齿数min 01Z 由表4-9查得:当401263.01101==-=Z x x 、、时,要求插齿刀的齿数不小于12 当401315.01101==-=Z x x 、、时,要求插齿刀的齿数不小于12 d .结果根据以上的选用,可确定插制内齿轮时的插齿刀的齿数、最小和最大变位系数我选取的插齿刀为:263.0,120.0,25min 01max 0101-===x x Z②选取的插齿刀参数: 25.1h 22.83d 25、75mm =d 3=m 00a 00===*a mm Z 、、、 所以:mm r r mm rb 24.35cos 61.41r 37.5mm =000a 0===α、、 mm a 5.225.376001=-=mm a a 67.2431cos 20cos 5.22cos cos 010101=︒︒⨯='='αα 83.349953.30sin 67.2424.3561.41sin 220101202001=︒⨯+-=''+-=αρa r r b a695.339953.30sin 933.4153.5275.60sin 2222221=︒⨯+-=''+-=αρa r r b a由于101ρρ>,所以不会发生内齿轮的过渡曲线干涉(五)、渐开线的开涉 1.切制外齿轮用齿条刀切制外齿轮时,不会产生顶切,所以只要考虑根切。