过渡过程的计算
- 格式:docx
- 大小:513.29 KB
- 文档页数:10

水力过渡过程计算嘿,朋友!咱们今天来聊聊水力过渡过程计算这回事儿。
你知道吗,水力过渡过程就像是一场水流的大冒险!想象一下,水在管道里、渠道中奔跑,突然遇到了一些状况,比如阀门关闭、水泵启动或者管道破裂。
这时候,水的流动状态可就发生了巨大的变化,就像一个调皮的孩子突然改变了玩耍的方式。
水力过渡过程计算,那可是相当重要的!比如说,在城市的供水系统中,如果不进行准确的计算,一旦出现紧急情况,比如突然停水或者水压骤变,那可就麻烦大啦!家里的水龙头可能不出水,洗澡洗到一半变成冷水澡,这得多难受啊!水力过渡过程计算其实就像是给水流规划路线。
我们要考虑水的速度、压力、流量这些因素,就像给一个旅行团安排行程,要考虑路程、时间和费用一样。
如果计算不准确,水流就可能“迷路”,造成各种问题。
比如说,在水电站中,水轮机的调节如果没有基于准确的水力过渡过程计算,那电力供应可能就会不稳定,一会儿亮堂堂,一会儿黑黢黢,这可咋整?再看看长距离的输水管道,如果不精心计算水力过渡过程,管道可能承受不住压力,出现破裂,那水就像脱缰的野马一样四处乱跑,这得造成多大的损失啊!那怎么进行水力过渡过程计算呢?这可不是拍拍脑袋就能搞定的。
得有专业的知识和工具。
就像厨师做菜要有好的食材和刀具一样。
我们要建立复杂的数学模型,把水流的各种特性都考虑进去。
这可不容易,就跟拼图一样,一块一块地拼凑,直到呈现出完整清晰的画面。
而且,还得根据实际情况不断调整参数,这就好比裁缝给人做衣服,得量体裁衣,不断修改,才能合身。
计算过程中,每一个数据都不能马虎,一个小差错可能就会导致整个结果大错特错,这难道不就像下棋走错一步满盘皆输吗?总之,水力过渡过程计算可不是一件轻松的事儿,但它又极其重要。
只有把这个计算做好了,我们的水利工程才能稳定运行,为我们的生活带来便利,不是吗?。




过渡态反应路径的计算⽅法及相关问题过渡态、反应路径的计算⽅法及相关问题SoberevaDepartment of Chemistry, University of Science and Technology Beijing, Beijing100083, China前⾔:本⽂主要介绍过渡态、反应路径的计算⽅法,并讨论相关问题。
由于这类算法极多,可以互相组合,限于精⼒不可能⾯⾯俱到展开,所以只介绍常⽤,或者实⽤价值有限但有启发性的⽅法。
⽂中图⽚来⾃相关⽂献,做了⼀定修改。
由于本⽂作为帖⼦发布,⽂中⽆法插⼊复杂公式,故⽂中尽量将公式转化为⽂字描述并加以解释,这样必然不如公式形式严谨,⽽且过于复杂的公式只能略过,但我想这样做的好处就是更易把握⽅法的梗概,有兴趣可以进⼀步阅读原⽂了解细节。
对于Gaussian中可以实现的⽅法,⽂中对其在Gaussian中的使⽤进⾏了⼀些讨论,希望能纠正⼀些⽹上流传的误区。
虽然绝⼤多数⼈不专门研究计算⽅法,其中很多⽅法也不会⽤到,但多了解⼀下对开阔思路就是很有好处的。
⽂中指的“反应”包括构象变化、异构化、单分⼦反应等任何涉及到过渡态的变化过程。
“反应物”与“产物”泛指这些过程的初态与末态。
“优化”若未注明,包括优化⾄极⼩点与优化⾄过渡态。
势能⾯就是⾼维的,但为了直观以及表述⽅便,⽂中⼀般⽤⼆维势能⾯模型来讨论,应推⼴⾄⾼维情况。
限于纯⽂本格式,向量、矩阵⽆法加粗表⽰,但容易⾃⾏判断。
⽬录:1、过渡态2、过渡态搜索算法2、1 基于初猜结构的算法2、1、1 ⽜顿-拉弗森法(Newton-Raphson,NR)与准⽜顿法(quasi-Newton,QN)2、1、2 AH⽅法(augmented Hessian)2、1、2、1 RFO法(Rational Function Optimization,有理函数优化)2、1、2、2 P-RFO法(Partitioned-RFO)2、1、2、3 QA法(Quadratic Approximation,⼆次逼近)2、1、2、4 TRIM法(trust-region image minimization,置信区域镜像最⼩化)2、1、2、5 在⾼斯中的常见问题2、1、3 GDIIS法(Geometry Direct Inversion in the Iterative Subspace)2、1、4 梯度模优化(gradient norm minimization)2、1、5 Dimer⽅法2、2 基于反应物与产物结构的算法2、2、1 同步转变⽅法(synchronous transit,ST)2、2、2 STQN⽅法(Combined Synchronous Transit and Quasi-Newton Methods)2、2、3 赝坐标法(pseudo reaction coordinate)2、2、4 DHS⽅法(Dewar-Healy-Stewart,亦称Saddle⽅法)与LTP⽅法(Line-Then-Plane)2、2、5 Ridge⽅法2、2、6 Step-and-Slide⽅法2、2、7 Müller-Brown⽅法2、2、8 CI-NEB、ANEBA⽅法2、3 基于反应物结构的算法2、3、1 最缓上升法(least steep ascent,shallowest ascent)2、3、2 本征向量/本征值跟踪法(eigenvector/eigenvalue following,EF。
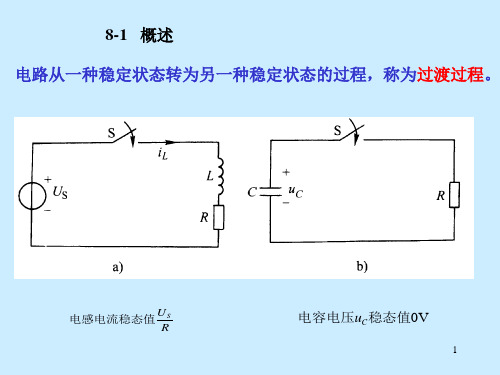
§8-4一阶电路的零输入响应仅含一个独立储能元件的电路称为一阶电路。
当电路中没有激励,仅由储能元件的初始储能引起的响应,称为零输入响应。
一、RC 电路的零输入响应如图8-4-1所示电路,开关S 原在位置1,电路已达稳态,电压源电压为U ,则u (0—)=U 。
在t =0时刻,S 由1切换至2,下面推求零输入响应u (t )、i (t )。
C 0C(式8-4-5)中的负号表示实际的电容放电电流方向与假设的参考方向相反。
i 还可以这样求,即:du将i =C 才代入上式得:du RC C +u=0 dt c(式8-4-2)(式8-4-2)是一个一阶线性常系数齐次微分方程,其特征方程为:RCs +1=01特征根为:s =--Rct齐次方程的通解为:u (t )=Ae st =Ae -RCc(式8-4-3)(式843)中的积分常数A 由初始条件确定。
由换路定则得:u c (0+)="J0-)=U 0,代入(式8-4-3),则有:u (0+)=A =Uc 0于是:u (t )=Ue -RC(式8-4-4)du i (t )=C-dtU--R 0-e RC(式8-4-5)CU -—-R-e RC过程维持的时间越短、过渡过程进行得越快。
下面以电容电压u 的衰减曲线为例,介绍求时间常数C 的图解法。
在图8-4-3中,从衰c则:通过实验得出uc 或i 的衰减曲线,再由图解法求出T,这在实际工作中是一种有用的方法。
图8-4-31"时间常数T 的大小取决于电路的结构和参数,而与激励无关减曲线上任一点P 作切线,它与t 轴的交点为Q ,从P 点作t 轴的垂直线,与t 轴的交点为P ', PQ =PP'-Cd ttUe Z——0 1UeT =T。
RC 串联电路的时间常数图8-4-2绘出了"。
«)、i (t )的曲线图,它们都按指数规律衰过程进展的快慢。
C 越大,过渡过程维持的时间越长、过渡过程进行得越慢;T 越小,过渡1T =RC 。
大波动过渡过程计算分析总结水电站输水系统和机组过渡过程的计算分析具有重要的意义,该计算分析对于机组参数GD2的选择、导叶关闭规律的确定、调压室参数的选择和管道线路的布置等方面都有重要的指导作用。
水电站过渡过程计算分析由大波动过渡过程计算分析和小波动过渡过程计算分析两部分组成。
以下对大波动过渡过程计算分析进行总结说明。
大波动过渡过程计算分析主要包含以下几个部分:①该类系统数学计算模型的建立和求解;②仿真计算程序的编制;③具体输水系统有关原始数据的准备(包含实际系统概化问题);④各种大波动控制工况的计算分析;⑤《水力过渡过程计算分析报告》的撰写。
一.数学计算模型的建立水电站输水系统数学模型由输水道数学模型和边界数学模型两部分构成。
1.输水道数学模型目前,输水道数学模型是根据一元总流流体的运动方程和连续方程,建立有压管道水力瞬变的弹性水锤基本方程组,然后利用特征线法对方程组进行简化、求解(这里暂不讨论无压输水道);由于在建立和求解模型的过程中,存在一些简化和假定条件,因此存在以下几个值得研究的问题:①现模型采用一元流假定,该假定在某些情况下不适用,应该改用“二元流”或“三元流”原理构造数模。
②该模型要求“同一段管道为单特性管”,因此须对非单特性管进行合理概化。
③该模型中管道阻力系数采用的是阀门关闭前稳态流动的值,实际应该采用动态的阻力系数。
④计算时间步长和波速调整的优化。
⑤含气水锤模型的建立。
2.边界数学模型不同边界具有不同的数学模型,目前基本边界的数学模型已较成熟,满足仿真计算精度要求。
3.数模的求解方法有压输水道数学模型采用特征线法求解;简单边界数学模型(如一元非线性代数方程)采用改进的不动点迭代法求解;复杂边界数学模型(如二元非线性代数方程组)采用牛顿-莱甫生法求解。
二.仿真计算程序的编制利用FORTRAN语言将已建立的数学模型和所选的求解方法编制成仿真计算程序。
同时,须注意以下几个问题:①水轮机特性曲线的变换(目前采用改进的Suter法)。
过渡态反应路径的计算方法及相关问题过渡态反应路径的计算是化学领域中的重要研究方向之一。
通过理解和计算过渡态反应路径,我们可以更好地理解反应机理、预测反应速率和优化催化剂等方面的问题。
本文将介绍一些常用的过渡态反应路径计算方法,并探讨与之相关的问题。
一、过渡态反应路径的计算方法1. 颜色指数法颜色指数法是一种常见的计算过渡态反应路径的方法。
该方法基于反应物和产物的颜色差异,通过可见光吸收光谱分析来确定过渡态的存在与否。
通过测量吸收峰的位置和强度,可以确定过渡态的反应路径。
2. 动力学方法动力学方法是计算过渡态反应路径的常用方法之一。
该方法通过实验观察物质在不同温度下的反应速率,来获得反应物到产物之间的激活能和反应路径。
常用的动力学方法包括Arrhenius方程和瞬态反应动力学等。
3. 量子化学计算方法量子化学计算方法是一种基于量子力学理论的计算过渡态反应路径的方法。
通过计算反应物和产物之间的势能面和振动光谱,可以确定过渡态的存在和反应路径。
常用的量子化学计算方法包括密度泛函理论和分子力学模拟等。
二、相关问题的讨论1. 过渡态的能量计算过渡态的能量计算是计算过渡态反应路径的关键步骤。
准确计算过渡态的能量可以提供反应物转化为产物所需的激活能信息。
这需要使用高精度的量子化学计算方法,并考虑溶剂效应和零点能等因素的影响。
2. 路径搜索算法路径搜索算法是计算过渡态反应路径的另一个重要问题。
由于反应物和产物之间可能存在多个反应路径,需要寻找最低能量的路径。
常用的路径搜索算法包括伸缩内坐标法、线性配位搜索法和改进的克拉米法等。
3. 动力学和热力学性质计算过渡态反应路径还涉及到动力学和热力学性质的研究。
动力学性质主要包括反应速率常数和活化能等,可以通过实验数据和量子化学计算来得到。
热力学性质则涉及到反应的热力学稳定性和平衡常数等,可以通过热力学计算和统计力学模拟来得到。
4. 催化剂的作用催化剂在过渡态反应路径中起着重要的作用。
关于共振过渡过程计算的数值方法摘要本文介绍了一种数值方法来计算一种固有频率下的共振过渡并为此进行了分析。
这种数值方法被用于计算涡轮叶片的共振过渡。
并把此结果与通过建立简化的并联模型并实现了很好的实验结果的完整共振过渡进行比较。
另外进行了一些参数研究例如结构阻尼共振过渡时间和激励振幅。
介绍在涡轮加速和减速的过程中,压气机的转子叶片和静子叶片受到增加或减少的频率和振幅的摆动压力,因此转子叶片和静子叶片的振动是非周期的,导致关于这些振动的计算变得困难。
但是对加速和减速涡轮过程的分析对研究共振过渡过程非常重要。
另外,关于完整的共振状态的过渡过程的计算需要不可接受的长时间计算。
共振状态的过渡已经被研究了很多年。
相关出版物是参考书目【1】和【2】和一些令人关注的论文。
在这些论文中,参考【3】和【6】,关于模型做一些低自由度的近似包围曲线已经发展成熟。
在【5】中研究了结构阻尼对共振过渡过程的影响。
在【7】中做了使用相位调制使转子共振过渡过程的振幅减小的研究。
在【8】中做了小激励下的非线性耦合系统共振过渡过程的理论研究。
在【4】中证明了对并联模型共振过渡过程的直接计算是可行的。
但是就作者的知识面而言,迄今为止对于完整模型此方面的计算是失败的。
本文提供了对共振过渡的一种简单的数值方法,并经过普遍地分析证明适用于研究涡轮叶片共振过渡过程。
并把此结果与发动机测试结果进行比较,但是因为公司所有权问题,本文中没有提供测试数据。
1、理论背景本文的主要内容是对于一个转动或非转动构件的振动过渡过程的调查研究。
假设过渡过程时间短和离心力是近似恒定的,在使用有限元法后,在构件本身加速和减速或一个不转动的构件因为构件附件的部件加速或减速而受到气动激励作用的情况下,构件(转动与否)振动的总体弹性方程如下:MX+CX+KX=P t,dim(M ) = dim(C ) = dim(K ) = n ⋅ n(1)dim( X ) = dim(P) = n ⋅1一个首要坐标系的转化,在C的正交性假设条件下,通过X = ∅Q,Q− 基本方程让步于l非耦合方程【9】:q i+2εiωi+ωi2q=h i t.i=1,l;l≤n,(2)和m i=∅i T M∅i,2εiωi=∅i T C∅i,k i=∅i T K∅i,ωi=k im i ,h i t=∅i T P(t)m i(3)在加速和减速的情况下,函数h i(t)是非周期的。
在本文中已假设,激励频率的变化是线性的如(4).理想情况下,激励作用下的振幅应该对每一个转子转速均适合,本文中已假设,振幅线性增加。
不变的幅度和过渡过程转速的最大振幅可以使用。
h i t=A i tsin(a i t22)(4)分析跟随一个独立方程(2)的假设解耦:q+2εωq+ω2q=h t=Atsin(at22)(5)对于已知的固有频率f=ω2π,最大的激励振幅A max,到达共振是的时间t res,阶次 j,相当转子转速R res,公式(5)中的a和A可以被简单估算:R res=60fj ,a=2πft res,A=A maxt res(6)不管怎样,实际的R res和t res取决于结构阻尼且实际稍大一些。
(5)的齐次解可被写为q h=c1q1t+c2q2(t), (7)q1t=e−εωt sin(ωD t),q1t=e−εωt cos(ωD t), (8)ωD=ω 1−ε2,c1和c2是积分常数。
此方法的使用,恒定变量引入特殊情况【10】作为形式上(5)的通解:q g=c1t q1t+c2t q2t(9)c1t=−h(τ)q2(τ)y(τ)dτ+c1(t0)tc 2 t = −h (τ)q 2(τ)y (τ)d τ+c 2(t 0)t 0(10)在当时边界值t 0和y =q 1q 2+q 2q 1。
在【11】中可以清楚得知,如果(1)中的激励P(t)是周期的(近似周期),(1)的特解也同样是周期的(近似周期)且轨道稳定。
像(4)中的激励不是周期或近似周期的,也会有完全周期性的振幅。
在【12】中研究了这种激励在线性和准线性系统上的渐进影响。
假设周期激励被作用在0边界条件下某一构件的解答提供了(5)特解的指数稳定性的证明。
此解答和任何边界条件下解答的比较表明:q g t ,0,0,0 −q g (t ,t 0,q 0,q 0) ≤ v i 2 2i=1,(11)v 1=−e −εωωD h (τ)e εωτsin ωD τ−t t 00d τ,(12) v 2= q i (t )(c i 0 −c i t 0 ) 2i=1,(13)因为t 0=const ,(12)中的齐次化积分受到限制,对此归于(8)中v 1,2→0伴随着t →+∞以指数方式。
因此同时证明了在解耦的假设下,(1)在周期激励下特解的指数稳定性。
在像(1)的方法中,为不同接触面(侧支、机械阻尼等等)的模型增加一些附加的条款,只需要小的修改则稳定性证明也同样会被提供:不同方法的分解针对于不同的状态单就接触表面的滑动、粘性和分离而言。
关于上述证明指数稳定性的重要推论如下:共振过渡过程的计算是不需要从0边界条件开始的(意思是转动速度从0开始)。
计算的开始只需从任何提前于共振过渡过程的边界条件就已足够。
为了得到最大限度的稳定解的短时间内的瞬间转化,则需要选择接近于真实条件的边界条件。
2、 参考模型为了验证应用程序的结果接近于被选择的涡轮叶片的共振过渡过程计算结果,一个参考模型—一个简化的并联模型—适合于对第一拍打模型形状的分析已经发展成熟了(图a )。
通常每个模型都会通过使用有限元模型用数值方法进行分析(第3章),但是简化模型逐步发展的方法并不是对每个模型都是使用的。
a)b)图1:简化并联模型a)涡轮叶片模型b)在这个模型中,替代质量来源于叶片模型(图1b)。
代替品的刚度和阻尼都是最优化的(刚度基于对涡轮叶片的有限元频率分析,阻尼基于构件的试验))来用于分析第一拍打模型形状。
激励力被模仿如下:F e=At sin at2,(14)2鉴于A和a取决于叶片的最大振幅区别于发动机试验和阶次激励。
假设试验结果预先不知,激励应该调整到一个水平以适应于叶片振幅级根据临界或叶片疲劳应力。
不同于线性增加,激励振幅的定义也是合理的:更多粗糙估计的恒量或二次时间或发动机速度都为了更精确的模拟。
作为一个参考解答—供以后解答—通过共振区的完整过渡,实例1F/11EO在不同条件下的计算已经完成。
在图2中引入了在排除发动机条件的情况下共振过渡过程包围曲线的形式。
此曲线是标准化的,如下:在横坐标上变量与旋转速度有关,然后关注红线变化情况,在纵坐标上是关于最大振幅的,假设谐波激励或激励和固有频率相同根据发动机情况而定。
在首要主题陈述之前,由于不同的影响,先描述了参考系的一些附加的参数研究。
目标是关于参数敏感性和依赖性普遍特征的调查。
正常地,所有的参数均会给出公差值。
首先,研究了共振过渡过程的时间变化(图3)。
图3中的最大振幅的曲线被展示在图4中。
此研究的结果如下:-过渡时间对最大振幅的非线性影响;-最大振幅间的相对小的偏差对于接近于发动机条件实例的分析模型。
图2:最高物块的共振过渡过程—包围曲线图3:共振过渡过程时间的影响(最高物块在并联模型中)图4:穿过标准化共振过渡过程时间的的标准化最大振幅第二个参数研究关于激励振幅(图5)。
激励振幅对大过渡振幅的影响是线性的—正如预期的(图6)。
既然如此,与其他的图表不同,纵坐标的标准化是关于最大振幅的,通过引用激励能级计算出。
图5:最大振幅的影响(最高物块在并联模型中)在最后的参数研究中,结构阻尼是变化的(图7:a)—增加,b)—结构阻尼的减少)。
我们可以看到此对最大过渡振幅的非线性影响。
图6:共振过渡过程的标准化最大振幅随标准化激励振幅的变化a)b)图7:结构阻尼的影响a)—增加,b)—减少(最高物块在并联模型中)图8:共振过渡过程的标准化最大振幅随标准化结构阻尼的变化3应用到涡轮叶片计算在任何边界条件下的共振过渡过程开始于共振开始的瞬间的可能性取决于对一个真正无覆盖涡轮叶片的共振过渡分析。
在图9中描述了叶片的几何模型和两种不同的激励力。
虽然只有翼型被描述,但是此模型依然包括一个长柄和一个圆盘断面。
激励力F e1和F e2是类型14的,F e1是作用于靠近翼尖的一个表面节点,F e2是作用于完整的翼型表面的(一边)。
两个激励都被调整以至于对第一拍打模型的稳态动力学分析引到了对受到两种激励的翼尖特征节点的振幅(图9)等于发动机试验测到的振幅。
结构阻尼以瑞利阻尼的®部分形式被提供,数值按照结构试验的经验确定,当然其值具有相同的作用在第二章中的简化模型中。
图9:分析叶片的模型对于这两种多变的,不明显的,和无覆盖的动力时积分均用有限元工具对模型进行网格化建模。
通过使用子方程式激励被模式化。
跟随特征节点的计算结果可以描述出标准化的包围曲线形式下的解答在切线上的数值。
“标准化”的意思是:尖端的最大振幅被分离出以区别于发动机试验结果并乘以100%。
在图10中描述了四条这样的包围曲线:-通过引用并联模型计算共振过渡过程在发动机加速的情况下(深蓝线);-“迅速”(直到过渡开始的时间=真实的发动机加速时间(3)“迅速”引用并联模型来进行共振过渡过程的相关计算(红线);-发动机在激励F e1的试验条件下用有线元分析法进行共振过渡过程的相关计算(黑线)(非常缓慢的加速以使振幅接近于谐波激励的频率与叶片固有频率相一致情况下的振幅);-在激励F e1作用下,用有限元法进行快速过渡过程的相关计算(浅蓝线)。
图10:通过参考并联模型计算出的完全共振过渡过程和在激励F e1作用下用有限元法计算出的不完全过渡过程的比较由不同的方法(在简化模型上的完全过渡过程的计算和在相同结构阻尼的有限元模型上的不完全过渡过程计算))计算出的结果(最大振幅)与实际发动机计算结果的一致性非常好。
通过有限元分析法计算出的不完全过渡过程的包围曲线可以看出稳定解的瞬间转换是明显的。
此外,还研究了不同激励类型和启动时间对过渡过程计算的影响。
图11表示了这些,可以看出使用不同的激励类型(F e1和F e2),结果是相同的。
图11:不同类型的激励对不完全共振过渡过程计算的影响与此相反,如果选择的最后一个点太接近于共振要点,则开始时间的影响是值得注意的(图12)。
图12:起始点对不完全共振过渡过程计算的影响4总结以上的工作记述了一种新的数值方法来快速计算一个构件经共振区的过渡过程。
构件可以是旋转的,也可以是非旋转的。
此方法也适用于涡轮或压气机的转子叶片或静子叶片。
此方法是经分析提供的,它不仅适用于任何共振情况(模型形状+阶次激励)的快速共振过渡过程的计算,还适用于有附加阻尼设计(机械,涡流等)的构件的快速共振过渡过程的计算。