过程控制的计算方法

统计过程控制中Z值的计算与分析统计过程控制中的Z值计算与分析是一种常见的统计方法，用于评估和控制一个过程的性能。

Z值计算的基础是正态分布的理论，通过计算样本的平均值与标准偏差来确定过程的性能是否达到标准要求。

下面是关于Z值计算与分析的详细介绍。

在统计过程控制中，假设一个过程的输出符合正态分布。

通过收集样本数据并计算其平均值和标准偏差，可以确定过程的性能。

Z值（也称为标准分数）是指一个观测值与平均值之间的差异，以标准差的单位来度量。

Z值的计算公式如下：Z=(X-μ)/σ其中，Z表示标准分数，X表示观测值，μ表示平均值，σ表示标准偏差。

通过计算每个样本的Z值，并将其与一个预先设置的阈值进行比较，可以确定过程是否正常运行。

如果Z值超过了阈值范围，就意味着过程存在异常或者超出了预定的控制限，需要采取相应的措施来调整过程。

Z值的分析可以提供一些重要的信息。

首先，Z值可以告诉我们一个过程的中心性能。

通常情况下，一个过程的Z值应接近于0，表示过程的中心值与目标值相近。

如果Z值显著偏离于0，就表明过程存在偏差或者漂移，需要进行调整。

其次，Z值还可以告诉我们一个过程的稳定性。

如果Z值较小且稳定，就表示过程运行稳定，处于控制状态；如果Z值较大或者不稳定，就表示过程存在变化或者波动，需要进行进一步的调查和改进。

Z值的分析还可以帮助我们识别过程中的特殊原因变异和常因变异。

特殊原因变异是指由于一些特殊因素引起的可辨识的异常值，例如机器故障、操作错误等；常因变异是指由于正常因素引起的正常波动，例如材料批次变化、环境温度变化等。

通过分析Z值，我们可以确定出现异常值的具体原因，并采取相应的措施来修正。

在进行Z值分析时，需要注意以下几个方面。

首先，样本大小要足够大，以确保结果的准确性和可靠性。

通常情况下，样本大小应大于30，但具体的要求可以根据具体情况来确定。

其次，选择合适的阈值来判断过程是否正常运行。

阈值的选择应综合考虑过程的要求、可靠性和成本等因素。

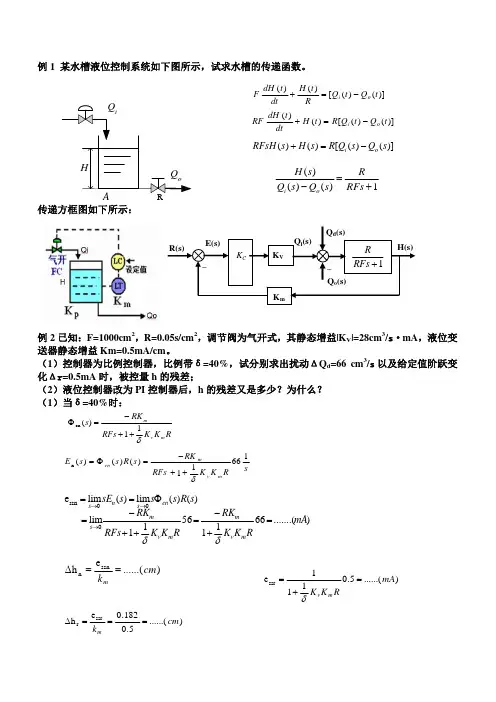
cpk计算公式及详细解释cpk（简称：Cp）是一个统计指标，它可以衡量特定程序的质量水平。

Cp评估是指对过程的控制状况（特别是在稳定的工艺过程中）的评估。

利用该指标，可以清楚地了解过程的控制水平，从而快速、有效地发现未控制的过程，从而可以采取措施进行优化，从而改善产品质量。

Cpk由以下公式组成：Cpk = min ( (T1 me) / (3σ) , (T2 me) / (3σ) ) 其中，T1和T2分别是规定的控制限，me是样本的平均值，σ是样本的标准差。

Cpk的计算方法及其解释：1、先确定规定控制限：既然要评估控制能力，那就要首先确定规定的控制限，即T1和T2，T1和T2分别是工艺上最高接受限度和最低接受限度，均为小于或等于0；2、计算样本的平均值：随后，利用样本测量结果计算出样本的平均值me，统一按照标准计算；3、计算样本的标准差：接下来，用测量结果计算样本的标准差σ，取其绝对值；4、计算Cpk：最后，使用以上参数计算Cpk，公式如上所示；5、解释Cpk：Cpk的值反映了过程的控制水平，Cpk的取值范围一般是0到10，若Cpk的取值在0-1之间，表明过程的控制水平低，需要重新检查并找出数据中的异常值；若Cpk的取值在1-2之间，表明过程的控制水平一般，需要多做努力，提高控制水平；若Cpk的取值在2-3之间，表明过程的控制水平良好，但仍可能存在较小改进空间；若Cpk的取值在3-4之间，表明过程的控制水平非常良好，此时可以进行改善，以进一步提高控制水平；若Cpk的取值大于4，表明过程的控制水平非常出色，可以放心使用。

Cpk具有以下优点：1、能够综合评估过程的控制水平：Cpk指标能够准确反映工艺过程中变量的控制水平；2、能够快速发现未控制的过程：Cpk指标可以很快地将未控制的过程从其他控制的过程中区分出来，因此可以确保良好的质量控制；3、能够及时对工艺过程进行优化：Cpk指标可以帮助发现问题，以及对工艺过程进行优化，从而改善产品的质量。

CPK的详细计算方法CPK是一种用于评估一个过程的稳定性和能力的统计量，它衡量了过程所产生的偏差与允许的偏差之间的差异。

该统计量常用于制造业，特别是在质量控制方面。

CPK是过程能力指数的一种度量，该指数通常用于描述一个过程是否稳定并且能够产生符合规格要求的产品。

具体来说，CPK通过比较过程的平均值和标准偏差与规格限制之间的关系来评估过程能力。

计算CPK需要以下几个步骤：1.收集数据：首先，我们需要收集一组与所评估过程相关的数据。

数据可以包括产品尺寸、重量、化学成分等等。

通常情况下，我们需要至少30个样本数据来进行计算。

2.计算平均值和标准偏差：根据收集到的数据，计算过程的平均值（记作x̄）和标准偏差（记作σ）。

平均值可以通过将所有数据相加并除以数据总数来得到，标准偏差可以通过计算每个数据点与平均值之间的差异，并将差异的平方求和后再除以数据总数减1来得到。

3.确定规格限制：在进行CPK计算之前，需要明确规格限制，即产品或过程在尺寸、重量等方面允许的上下限。

4.计算过程上下控制限：根据收集到的数据，可以利用统计方法计算出过程的上下控制限。

上控制限可以通过将平均值加上3倍的标准偏差来得到，下控制限可以通过将平均值减去3倍的标准偏差来得到。

5.计算CPK值：根据已有的数据和计算结果CPK = min((上控制限 - 平均值) / (3 * 标准偏差), (平均值 - 下控制限) / (3 * 标准偏差))其中，上控制限和下控制限是在步骤4中计算得到的控制限值。

6.解读CPK值：根据CPK值的大小，可以对过程的稳定性和能力进行评估。

一般来说，CPK值大于1表示过程能够满足规格要求，CPK值大于1.33表示过程的效果更好，CPK值大于2表示过程非常稳定。

通过以上的计算步骤，就可以获得一个准确评估过程稳定性和能力的CPK值。

这个指标对于制造业的质量控制非常重要，能够帮助企业识别并改进不符合规格要求的产品或过程，从而提高产品质量，降低生产成本，并提升客户满意度。

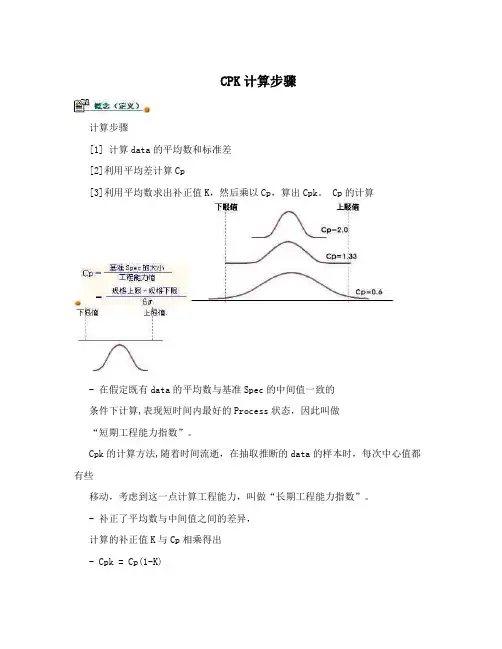
CPK计算步骤计算步骤[1] 计算data的平均数和标准差[2]利用平均差计算Cp[3]利用平均数求出补正值K，然后乘以Cp，算出Cpk。

Cp的计算- 在假定既有data的平均数与基准Spec的中间值一致的条件下计算,表现短时间内最好的Process状态，因此叫做“短期工程能力指数”。

Cpk的计算方法,随着时间流逝，在抽取推断的data的样本时，每次中心值都有些移动，考虑到这一点计算工程能力，叫做“长期工程能力指数”。

- 补正了平均数与中间值之间的差异，计算的补正值K与Cp相乘得出- Cpk = Cp(1-K)工程能力指数的测定值大致分为Cp和Cpk两种。

Cp是在假定既有data的平均数与基准Spec的中间值一致的条件下计算的。

短期工程能力指数”。

表示的是短时间内最好的Process状态，因此叫做“就具体数值的计算来看，首先根据data计算出平均数与标准差，利用标准差按如下公式计算出Cp的值。

例如，在钢板的生产中，产品的规格上限是40毫米，规格下限是35毫米，那么Cp分子部分的(规格上限-规格下限)就是5毫米吧。

另外，如果根据所生产钢板的厚度测定的data求得的标准差是0.8毫米，那么Cp的值就是5/(6×0.8)=1.04。

下面是Cpk的计算方法，即利用平均数求出如下的补正值K，然后乘以Cp即可。

Cpk = Cp(1-K)K如果是0的话，Cp与Cpk一致。

测定值的平均数离中间值越远，Cpk就越小，表示工程能力的不足。

因此，Cpk是考虑到“时间的流逝”、“每次应用测定的data的样本时”中心值稍微有所不同的问题来计算出的，叫做“长期工程能力指数”。

什么是SPC?SPC即统计过程控制(Statistical Process Control)。

SPC主要是指应用统计分析技术对生产过程进行实时监控，科学的区分出生产过程中产品质量的随机波动与异常波动，从而对生产过程的异常趋势提出预警，以便生产管理人员及时采取措施，消除异常，恢复过程的稳定，从而达到提高和控制质量的目的。

统计过程控制程序1目的通过应用统计技术，对公司有关的数据进行收集分析，以证实质量管理体系的适宜性和有效性，确保过程能力及产品质量得到有效控制和改进。

2范围本程序适用于公司顾客要求和需做统计过程控制(Cp、Cpk、Pp、Ppk、Cmk、PPM)的所有过程和产品。

3职责3.1品质管理部：数据分析的归口管理部门，负责统计技术应用的指导、检查、分析和管理；并对检验数据进行收集、整理、统计、分析，提出改进要求。

3.2工程技术：确定过程和产品的技术要求、控制要求，并组织进行改进。

3.3**事业部：负责收集、统计生产过程的数据，并根据SPC控制图研究结果对过程、产品实施改进。

3.4其它部门：负责与本部门有关的数据的收集、分析与传递。

4定义4.1统计过程控制(SPC)利用统计技术把数据转换成过程状态信息，以便确认、纠正和改进过程效能。

4.2统计过程控制体系为实施SPC技术管理所需的组织机构、程序、过程和资源。

4.3工序能力(B)处于稳定、标准状态下，工序的实际加工能力，表达式B=6o=6S，其影响因素是人、机、料、法、环、测。

4.4稳定过程能力(Cp)衡量工序能力对产品规格要求满足程度的数量值，是规格范围(T)与工序能力(B)的比值，表达式Cp=T/B(T二规格上限Tu 一规格下限TL)。

4.5稳定过程能力指数(Cpk)是一项有关稳定过程能力的指数，计算时需同时考虑过程数的趋势及该趋势接近于规格界限的程度。

4.6初期过程能力(Pp)是一项类似于Cp的指数，但计算时是以新产品的初期过程的性能。

4.7初期过程能力指数(Ppk)1是一项类似于Cpk的指数，但计算时是以新产品的初期过程性能研究所得的数据为基础。

4.8质量水准(PPM)每百万个零件不合格数，指一种根据实际的缺陷材料来反映过程能力的一种方法，PPM数据常用来优先制定纠正措施。

4.9设备能力指数(Cmk)反映机械设备在受控条件下，当其人/料/法不变时的生产能力大小。

SPC计算公式范文SPC（Statistic Process Control）是一种通过统计方式对过程进行控制的方法，它可以帮助我们检测并识别过程中的特殊因子，并及时采取纠正措施，以保持过程处于控制状态。

SPC计算公式是SPC方法中常用的一些统计计算公式，包括均值、标准差、控制图等。

以下是SPC方法中常用的几个计算公式。

1. 均值（Mean）均值是一组数据的平均值，用于描述数据集中的集中趋势。

均值的计算公式如下：Mean = (x1 + x2 + x3 + ... + xn) / n其中，x1、x2、x3等是数据集中的各个数据点，n是数据点的个数。

2. 范围（Range）范围表示一组数据的最大值和最小值之间的差值，用于描述数据集中的离散程度。

范围的计算公式如下：Range = xmax - xmin其中，xmax是数据集中的最大值，xmin是数据集中的最小值。

3. 标准差（Standard Deviation）标准差表示数据集中各个数据点与均值之间的离散程度，用于描述数据集的分布情况。

标准差的计算公式如下：Standard Deviation = √ ((x1 - M ean)² + (x2 - Mean)² + (x3 - Mean)² + ... + (xn - Mean)² ) / (n-1)其中，x1、x2、x3等是数据集中的各个数据点，Mean是数据集的均值，n是数据点的个数。

4. 方差（Variance）方差是标准差的平方，也是描述数据集的分布情况的统计指标。

方差的计算公式如下：Variance = ((x1 - Mean)² + (x2 - Mean)² + (x3 - Mean)² + ... + (xn - Mean)² ) / (n-1)其中，x1、x2、x3等是数据集中的各个数据点，Mean是数据集的均值，n是数据点的个数。

Spc应用计算公式SPC(统计过程控制)是一种使用统计方法来监测和控制过程稳定性和能力的方法。

在SPC中，有一些常用的计算公式，用于帮助我们计算和分析数据，从而做出相应的决策。

本文将介绍一些常见的SPC应用计算公式。

1. 总体平均值（X-Bar）的计算公式:X-Bar = ΣXi / n其中，Xi是每个样本的值，n是样本的数量。

2.总体标准差（R）的计算公式:R = Max(Xi) - Min(Xi)其中，Xi是每个样本的值。

3. 级别平均值（X-Double Bar）的计算公式:X-Double Bar = ΣX-Bar / k其中，X-Bar是每个样本的平均值，k是样本组的数量。

4. 标准偏差（sbar）的计算公式:sbar = Σs / k其中，s是每个样本的标准差，k是样本组的数量。

5.控制图中的控制限计算公式:上控制限 (UCL) = X-Double Bar + A2 * R中心线 (CL) = X-Double Bar下控制限 (LCL) = X-Double Bar - A2 * R其中，A2是常数，根据样本组大小来确定。

6.总体标准差（σ）的计算公式:σ = sbar * √(1 + (1 / k))其中，sbar是每个样本的标准差，k是样本组的数量。

7.过程能力指数(Cp)的计算公式:Cp=(USL-LSL)/(6*σ)其中，USL是上限规范限制，LSL是下限规范限制，σ是总体标准差。

8. 过程性能指数 (Cpk) 的计算公式:Cpk = min[(USL - X-Bar) / (3 * s), (X-Bar - LSL) / (3 * s)]其中，USL是上限规范限制，LSL是下限规范限制，X-Bar是样本平均值，s是样本标准差。

9.异常规则检测的计算公式:-1σ规则:如果一个点落在CL±1σ之外，表示过程存在特殊因素。

-2σ规则:如果一个点落在CL±2σ之外，表示过程可能出现一般性问题。

统计过程控制中Z 值的计算与分析Z 值是统计过程控制SPC(Statistical Process Control)的常用统计量之一，本文将就Z 的计算与分析做一简单介绍。

一、Z 值的计算公式Z 值是某一特征值与均值之间标准偏差的数量，其是一个相对量。

Z 值的计算公式为：()σµ−=x z 其中：x-某一特征值；μ-总体均值；σ-总体的标准差在实际中都是通过抽样来估计总体，则Z 值的计算公式变化为：()sx x z −=其中：x-某一特征值；x -样本均值；s-样本的标准差如果一个过程仅有单侧公差时，则：σµσµLSL Z USL Z LSL USL −=−=其中：USL-上规范线；LSL-下规范线；μ-总体均值；σ-总体的标准差二、Z 的计算与分析如果有一个学生在中考的数学和英语成绩分别为112和108，他的成绩好吗？是数学成绩还是英语成绩相对更好一些？通过Z 值的计算就可以看出该学生的成绩距离均值的程度，也可以看出来哪个成绩相对更好一些。

如果已知全市数学成绩的均值为108，标准差为21，英语成绩的均值为97，标准差为18，那么：σσ0.6118111897-1080.1921421108-112======英语数学Z Z 将Z 值转化为百分数常用以下几种方式：（1）查正态分布-Z 值表；（2）通过Excel 的公式“=Normsdist（x）”计算；（3）利用一些软件，例如：minitab、Z 值-百分数计算器。

通过上述三种方法里的任意一种，我们可知：该学生数学成绩对应的百分数为57.53%，英语成绩对应的百分数为72.91%，通过下图可以看到该学生的数学和英语成绩在总体中的位置，同时也可以看出英语的成绩相对要好于数学成绩。

数学英语在实际生活中有一些过程仅有规范上线或规范下线。

例如：某产品的安装时间规定不允许超过120分钟，经抽样10个样本的安装时间分别为：100、99、101、125、100、123、100、123、96、90、98、116，则其均值为：104.8，标准差为：12.03，则：σ26.103.122.1503.128.104120==−=USL Z如果样本具有随机性和代表性，从上图可以看出，在实际的安装过程中89.6%的产品安装时间小于120分钟，同时10.4%的产品安装时间会超过120分钟，这样的过程显然是不能满足要求的，经过改进后又随机抽取了10个样本，其分别为：60、75、99、88、65、72、75、72、87、65，则其均值为：78.5，标准差为：12.14，则：σ42.314.125.4114.125.78120==−=USL Z由上面的计算和图示对比，可以清楚的看到改进的效果非常的明显，改进后仅有0.03%的产品安装时间会超过120分钟。