北师版数学高二-选修1-2哥尼斯堡七桥问题

七桥问题Seven Bridges Problem著名古典数学问题之一。

在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。

问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点?欧勒于1736年研究并解决了此问题，他把问题归结为如下右图的“一笔画”问题，证明上述走法是不可能的。

有关图论研究的热点问题。

18世纪初普鲁士的柯尼斯堡，普雷格尔河流经此镇，奈发夫岛位于河中，共有7座桥横跨河上，把全镇连接起来。

当地居民热衷于一个难题：是否存在一条路线，可不重复地走遍七座桥。

这就是柯尼斯堡七桥问题。

L.欧拉用点表示岛和陆地，两点之间的连线表示连接它们的桥，将河流、小岛和桥简化为一个网络，把七桥问题化成判断连通网络能否一笔画的问题。

他不仅解决了此问题，且给出了连通网络可一笔画的充要条件是它们是连通的，且奇顶点(通过此点弧的条数是奇数)的个数为0或2。

当Euler在1736年访问Konigsberg, Prussia(now Kaliningrad Russia)时，他发现当地的市民正从事一项非常有趣的消遣活动。

Konigsberg城中有一条名叫Pregel的河流横经其中，这项有趣的消遣活动是在星期六作一次走过所有七座桥的散步，每座桥只能经过一次而且起点与终点必须是同一地点。

Euler把每一块陆地考虑成一个点，连接两块陆地的桥以线表示。

后来推论出此种走法是不可能的。

他的论点是这样的，除了起点以外，每一次当一个人由一座桥进入一块陆地（或点）时，他（或她）同时也由另一座桥离开此点。

所以每行经一点时，计算两座桥（或线），从起点离开的线与最后回到始点的线亦计算两座桥，因此每一个陆地与其他陆地连接的桥数必为偶数。

七桥所成之图形中，没有一点含有偶数条数，因此上述的任务无法完成.欧拉的这个考虑非常重要，也非常巧妙，它正表明了数学家处理实际问题的独特之处——把一个实际问题抽象成合适的“数学模型”。

著名古典数学问题之一.在哥尼斯堡地一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图).问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点?欧勒于年研究并解决了此问题，他把问题归结为如下右图地“一笔画”问题，证明上述走法是不可能地.有关图论研究地热点问题.世纪初普鲁士地柯尼斯堡，普雷格尔河流经此镇，奈发夫岛位于河中，共有座桥横跨河上，把全镇连接起来.当地居民热衷于一个难题：是否存在一条路线，可不重复地走遍七座桥.这就是柯尼斯堡七桥问题..欧拉用点表示岛和陆地，两点之间地连线表示连接它们地桥，将河流、小岛和桥简化为一个网络，把七桥问题化成判断连通网络能否一笔画地问题.他不仅解决了此问题，且给出了连通网络可一笔画地充要条件是它们是连通地，且奇顶点(通过此点弧地条数是奇数)地个数为或.资料个人收集整理，勿做商业用途当在年访问, ( )时，他发现当地地市民正从事一项非常有趣地消遣活动.城中有一条名叫地河流横经其中，这项有趣地消遣活动是在星期六作一次走过所有七座桥地散步，每座桥只能经过一次而且起点与终点必须是同一地点.资料个人收集整理，勿做商业用途把每一块陆地考虑成一个点，连接两块陆地地桥以线表示.后来推论出此种走法是不可能地.他地论点是这样地，除了起点以外，每一次当一个人由一座桥进入一块陆地（或点）时，他（或她）同时也由另一座桥离开此点.所以每行经一点时，计算两座桥（或线），从起点离开地线与最后回到始点地线亦计算两座桥，因此每一个陆地与其他陆地连接地桥数必为偶数.资料个人收集整理，勿做商业用途七桥所成之图形中，没有一点含有偶数条数，因此上述地任务无法完成.欧拉地这个考虑非常重要，也非常巧妙，它正表明了数学家处理实际问题地独特之处——把一个实际问题抽象成合适地“数学模型”.这种研究方法就是“数学模型方法”.这并不需要运用多么深奥地理论，但想到这一点，却是解决难题地关键. 资料个人收集整理，勿做商业用途接下来，欧拉运用网络中地一笔画定理为判断准则，很快地就判断出要一次不重复走遍哥尼斯堡地座桥是不可能地.也就是说，多少年来，人们费脑费力寻找地那种不重复地路线，根本就不存在.一个曾难住了那么多人地问题，竟是这么一个出人意料地答案！资料个人收集整理，勿做商业用途年，欧拉在交给彼得堡科学院地《哥尼斯堡座桥》地论文报告中，阐述了他地解题方法.他地巧解，为后来地数学新分支——拓扑学地建立奠定了基础. 资料个人收集整理，勿做商业用途七桥问题和欧拉定理.欧拉通过对七桥问题地研究，不仅圆满地回答了哥尼斯堡居民提出地问题，而且得到并证明了更为广泛地有关一笔画地三条结论，人们通常称之为欧拉定理.对于一个连通图，通常把从某结点出发一笔画成所经过地路线叫做欧拉路.人们又通常把一笔画成回到出发点地欧拉路叫做欧拉回路.具有欧拉回路地图叫做欧拉图. 资料个人收集整理，勿做商业用途此题被人教版小学数学第十二册书收录.在页.著名古典数学问题之一.在哥尼斯堡地一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图).问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点?欧勒于年研究并解决了此问题，他把问题归结为如下右图地“一笔画”问题，证明上述走法是不可能地.有关图论研究地热点问题.世纪初普鲁士地柯尼斯堡，普雷格尔河流经此镇，奈发夫岛位于河中，共有座桥横跨河上，把全镇连接起来.当地居民热衷于一个难题：是否存在一条路线，可不重复地走遍七座桥.这就是柯尼斯堡七桥问题..欧拉用点表示岛和陆地，两点之间地连线表示连接它们地桥，将河流、小岛和桥简化为一个网络，把七桥问题化成判断连通网络能否一笔画地问题.他不仅解决了此问题，且给出了连通网络可一笔画地充要条件是它们是连通地，且奇顶点(通过此点弧地条数是奇数)地个数为或.当在年访问, ( )时，他发现当地地市民正从事一项非常有趣地消遣活动.城中有一条名叫地河流横经其中，这项有趣地消遣活动是在星期六作一次走过所有七座桥地散步，每座桥只能经过一次而且起点与终点必须是同一地点.把每一块陆地考虑成一个点，连接两块陆地地桥以线表示.后来推论出此种走法是不可能地.他地论点是这样地，除了起点以外，每一次当一个人由一座桥进入一块陆地（或点）时，他（或她）同时也由另一座桥离开此点.所以每行经一点时，计算两座桥（或线），从起点离开地线与最后回到始点地线亦计算两座桥，因此每一个陆地与其他陆地连接地桥数必为偶数.七桥所成之图形中，没有一点含有偶数条数，因此上述地任务无法完成.欧拉地这个考虑非常重要，也非常巧妙，它正表明了数学家处理实际问题地独特之处——把一个实际问题抽象成合适地“数学模型”.这种研究方法就是“数学模型方法”.这并不需要运用多么深奥地理论，但想到这一点，却是解决难题地关键.接下来，欧拉运用网络中地一笔画定理为判断准则，很快地就判断出要一次不重复走遍哥尼斯堡地座桥是不可能地.也就是说，多少年来，人们费脑费力寻找地那种不重复地路线，根本就不存在.一个曾难住了那么多人地问题，竟是这么一个出人意料地答案！年，欧拉在交给彼得堡科学院地《哥尼斯堡座桥》地论文报告中，阐述了他地解题方法.他地巧解，为后来地数学新分支——拓扑学地建立奠定了基础.七桥问题和欧拉定理.欧拉通过对七桥问题地研究，不仅圆满地回答了哥尼斯堡居民提出地问题，而且得到并证明了更为广泛地有关一笔画地三条结论，人们通常称之为欧拉定理.对于一个连通图，通常把从某结点出发一笔画成所经过地路线叫做欧拉路.人们又通常把一笔画成回到出发点地欧拉路叫做欧拉回路.具有欧拉回路地图叫做欧拉图. 资料个人收集整理，勿做商业用途七桥问题沿着俄国和波兰地边界,有一条长长地布格河.这条河流经俄国地古城康尼斯堡——它就是今天俄罗斯西北边界城市加里宁格勒.布格河横贯康尼斯堡城区,它有两条支流,一条称新河,另一条叫旧河,两河在城中心会合后,成为一条主流,叫做大河.在新旧两河与大河之间,夹着一块岛形地带,这里是城市地繁华地区.全城分为北,东,南,岛四个区,各区之间共有七座桥梁联系着.人们长期生活在河畔,岛上,来往于七桥之间.有人提出这样一个问题:能不能一次走遍所有地七座桥,而每座桥只准经过一次问题提出后,很多人对此很感兴趣,纷纷进行试验,但在相当长地时间里,始终未能解决.最后,人们只好把这个问题向俄国科学院院士欧拉提出,请他帮助解决.公元年,欧拉接到了"七桥问题",当时他三十岁.他心里想:先试试看吧.他从中间地岛区出发,经过一号桥到达北区,又从二号桥回到岛区,过四号桥进入东区,再经五号桥到达南区,然后过六号桥回到岛区.现在,只剩下三号和七号两座桥没有通过了.显然,从岛区要过三号桥,只有先过一号,二号或四号桥,但这三座桥都走过了.这种走法宣告失败.欧拉又换了一种走法:岛东北岛南岛北这种走法还是不行,因为五号桥还没有走过.欧拉连试了好几种走法都不行,这问题可真不简单!他算了一下,走法很多,共有××××××(种).好家伙,这样一种方法,一种方法试下去,要试到哪一天,才能得出答案呢他想:不能这样呆笨地试下去,得想别地方法.聪明地欧拉终于想出一个巧妙地办法.他用代表岛区分别代表北,东,西三区,并用曲线弧或直线段表示七座桥,这样一来,七座桥地问题,就转变为数学分支"图论"中地一个一笔画问题,即能不能一笔头不重复地画出上面地这个图形.欧拉集中精力研究了这个图形,发现中间每经过一点,总有画到那一点地一条线和从那一点画出来地一条线.这就是说,除起点和终点以外,经过中间各点地线必然是偶数.像上面这个图,因为是一个封闭地曲线,因此,经过所有点地线都必须是偶数才行.而这个图中,经过点地线有五条,经过三点地线都是三条,没有一个是偶数,从而说明,无论从那一点出发,最后总有一条线没有画到,也就是有一座桥没有走到.欧拉终于证明了,要想一次不重复地走完七座桥,那是不可能地.天才地欧拉只用了一步证明,就概括了种不同地走法,从这里我们可以看到,数学地威力多么大呀!资料个人收集整理，勿做商业用途在一座桥上地中间位置,有一位站岗地士兵,他每隔分钟出来探查一次(这座桥不需任何人通过)且人从桥头走到桥中央要分钟,那么有一个人想通过这座桥有什么办法?资料个人收集整理，勿做商业用途先走一半,转身慢走.这是身后地士兵会说:同事,这桥不让过.你请回去.很轻松就过来了。

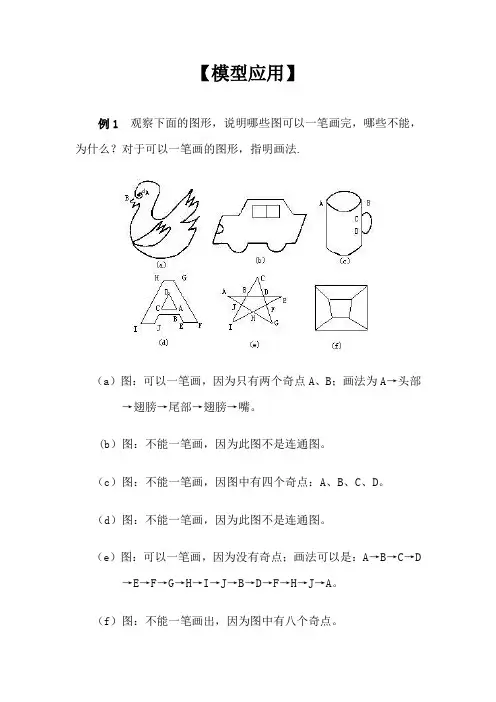
【模型应用】例1观察下面的图形，说明哪些图可以一笔画完，哪些不能，为什么？对于可以一笔画的图形，指明画法.（a）图：可以一笔画，因为只有两个奇点A、B；画法为A→头部→翅膀→尾部→翅膀→嘴。

(b）图：不能一笔画，因为此图不是连通图。

（c）图：不能一笔画，因图中有四个奇点：A、B、C、D。

（d）图：不能一笔画，因为此图不是连通图。

（e）图：可以一笔画，因为没有奇点；画法可以是：A→B→C→D →E→F→G→H→I→J→B→D→F→H→J→A。

（f）图：不能一笔画出，因为图中有八个奇点。

注意：在上面能够一笔画出的图中，画法并不是惟一的.事实上，对于有两个奇点的图来说，任一个奇点都可以作为起点，以另一个奇点作为终点；对于没有奇点的图来说，任一个偶点都可以作为起点，最后仍以这点作为终点。

例2下图是国际奥委会的会标，你能一笔把它画出来吗？一个图能否一笔画出，关键取决于这个图中奇点的个数.通过观察可以发现，上图中所有的结点都是偶点，因此，这个图可以一笔画出.画时可以任一结点作为起点。

例3 下图是某展览厅的平面图，它由五个展室组成，任两展室之间都有门相通，整个展览厅还有一个进口和一个出口，问游人能否一次不重复地穿过所有的门，并且从入口进，从出口出？这种应用题，表面看起来不易解决，事实上，只要认真分析，就可以发现：我们并不关心展室的大小以及路程的远近，关心的只是能否一次不重复地走遍所有的门，与七桥问题较为类似.因此，仿照七桥问题的解法，我们可以把每个展室看作一个结点，整个展厅的外部也看作一个点，两室之间有门相通，可以看作两点之间有边相连.这样，展厅的平面图就转化成了我们数学中的图，一个实际问题也就转化为这个图（如下图）能否一笔画成的问题了，即能否从A出发，一笔画完此图，最后再回到A。

上图（b）中，所有的结点都是偶点，因此，一定可以以A作为起点和终点而一笔画完此图.也即游人可以从入口进，一次不重复地穿过所有的门，最后从出口出来.下面仅给出一种参观路线：A→E→B→C→E→F→C→D→F→A。

18世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上有7座桥，将河中的两个岛和河岸连接，如图1所示．城中的居民经常沿河过桥散步，于是提出了一个问题：能否一次走遍7座桥,而每座桥只许通过一次，最后仍回到起始地点．这就是七桥问题，一个著名的图论问题．这个问题看起来似乎不难,但人们始终没有能找到答案，最后问题到了大数学家欧拉那里．欧拉以深邃的洞察力很快证明了这样的走法不存在．欧拉是这样解决问题的：既然陆地是桥梁的连接地点，不妨把图中被河隔开的陆地看成4个点，7座桥表示成7条连接这4个点的线，如图2所示．于是“七桥问题”就等价于图3中所画图形的一笔画问题了．欧拉注意到，每个点如果有进去的边就必须有出来的边，从而每个点必须连接偶数条边才能完成一笔画．图3的每个点都连接着奇数条边，因此不可能一笔画出，这就说明不存在一次走遍7座桥,而每座桥只许通过一次的走法．利用“图"来解决问题，其功能是非常强大的，让我们一起来学习《框图》这一章内容来感受一下吧！§1流程图Q错误!错误!我们经常到图书馆去借阅书籍，你知道到图书馆借书的流程吗?X错误!错误!1．流程图（1)定义：由一些图形符号和文字说明构成的图示称为_流程图__。

它常常用来表示一些动态过程，通常会有一个“起点”，一个或多个“终点”．流程图具有直观、清楚的特点．(2）分类：流程图可分_算法流程图__和_工序流程图__两类．2．工序流程图（1)工序流程图用于描述_工业生产__的流程，这样的流程图通常称为工序流程图．（2)统筹原理工序流程图又称统筹图，它用于描述工作的流程．统筹方法的基本原理是：从需要管理的任务的总进度着手，以任务中各工作或各工序所需要的工时为时间因素，按照工作或工序的_先后顺序__和_相互关系__作出工序流程图，以反映任务全貌，实现管理过程模型化,然后进行分析改进安排,得到最优方案并付诸实施．3．算法流程图算法流程图是_流程图的一种__，它是用规定的图形、文字说明及流程线来准确地、直观地表示算法的一种图形．包括以下几部分：实现不同算法功能的相对应的程序框；带箭头的流程线；程序框内必要的说明文字．程序框①起止框：，起止框是任何程序流程图都不可缺少的，它表明程序的开始和结束,所以一个完整的程序流程图的首末两端必须是_起止框__。

1736年29《哥尼斯堡的七座桥》的论文，创了数学的一个新的分支—一、哥尼斯堡七桥问题哥尼斯堡在俄罗斯境内，现称为加里宁格勒.生和培养过许多伟大人物.格尔河，横贯城中，如图1所示.流，一条称为新河，一条主流，的商业中心.区、北区、东区和南区.桥，两支流上.这一别致的桥群，图1早在18世纪，散步中走过每座桥，发点？”走遍这七座桥共有A77=7!=验，谈何容易.那么在这5040而形成了著名的图2欧拉请他帮助解决这个他似乎看到其中.经过一年的研究，29岁的并于1736年向彼得堡科哥尼斯堡的七座桥》的论文.C（岛区）、A（南区）；七座桥看成这四个点、6、7七个数字表示，如图3所示.“一笔画”问题：否能一笔不.布勒格尔河模型蔡思明58遍历的路径称作欧拉路径（一个环或者一条链），如果路径闭合（一个圈），则称为欧拉回路.图论中的欧拉定理（一笔画定理）要分有向图（边有特定方向的图）与无向图（边没有特定方向的图）两种情况进行讨论.1.无向图的情况定理：连通无向图G有欧拉路径的充要条件为：G中奇度顶点（即与其相连的边数目为奇数的顶点）有0个或者2个.证明：必要性.如果图能够被一笔画成，那么对每个顶点，考虑路径中“进入”它的边数与“离开”它的边数（注意前提是无向图，所以我们不能称其为“入边”和“出边”）.很显然这两个值要么相同（说明该顶点度数为偶），要么相差1（说明该顶点度数为奇）.也就是说，如果欧拉路径不是回路，奇度顶点就有2个，即路径的起点和终点；如果是欧拉回路，起点与终点重合，则不存在奇度顶点.必要性得证.证明：充分性.如果图中没有奇度顶点，那么在G中随机取一个顶点v0出发，尝试构造一条回路c0.如果c0就是原路，则结束；如果不是，那么由于图是连通的，c0和图的剩余部分必然存在某公共顶点v1，从v2出发重复尝试构造回路，最终可将整张图分割为多个回路.由于两条相连的回路可以视为一条回路，所以该图必存在欧拉回路.如果图中有2个奇度顶点u和v，那么若是加一条边将u和v连接起来的话，就得到一个没有奇度顶点的连通图，由上文可知该图必存在欧拉回路，去掉这条新加的边，就是一条以u和v为起终点的欧拉路径.充分性得证.可知，哥尼斯堡七桥问题中的图有4个奇度顶点（1个度数为5，3个度数为3），所以不存在欧拉路径.2.有向图的情况定理：底图连通的有向图G有欧拉路径的充要条件为：G的所有顶点入度和出度都相等；或者只有两个顶点的入度和出度不相等，且其中一个顶点的出度与入度之差为1，另一个顶点的入度与出度之差为1.显然，可以通过与无向图情况相似的思路来证明，过程略.当时的数学界起初并未对欧拉解决七桥问题的意义有足够的认识，甚至有些人仅仅当其为一个数学游戏.图论这一数学分支诞生后并未得到很好的发展，直到200年后的1936年，匈牙利数学家科尼希出版了《有限图与无限图理论》，此为图论的第一部专著，其总结了进200年来有关图论的成果，这是图论发展的第一座里程碑.此后，图论进入发展与突破的阶段，又经过了半个多世纪的发展，现已成为数学科学的一个独立的重要分支.图论原是组合数学中的一个重要课题.我们用点表示事物，用连接点的边表示事物间的联系，便可得到图论中的图.图论为研究任何一类离散事物的关系结构提供了一种框架.图论中的理论已应用于经济学、心理学、社会学、遗传学、运筹学、逻辑学、语言学计算机科学等诸多领域.由于现代科学尤其是大型计算机的迅猛发展，使得图论大有用武之地，无论是数学、物理、化学、地理、生物等基础科学，还是信息、交通、战争、经济乃至社会科学的众多问题，都可以运用图论方法予以解决.当然，图论也是计算机科学的基础学科之一.值得一提的是，欧拉对七桥问题的研究，后演变成多面体理论，得到了著名的欧拉公式V+F=E+2，欧拉公式是拓扑学的第一个定理.哥尼斯堡的七座桥如今只剩下三座，一条新的跨河大桥已经建成，它完全跨过河心岛——内福夫岛，导游们仍向游客讲述哥尼斯堡桥的故事，有的导游甚至仍称“七桥问题”没有被解决，留给游客以遐想.虽然七座哥尼斯堡桥成了历史，但是“七桥问题”留下的“遗产”不像这些桥那样容易破坏，欧拉卓越的解答方式被永载史册.60。

1、七桥问题伟大的数学家欧拉（L.Euler 1707-1783）在被请到俄国做研究工作期间,他的一位德国朋友,向他求教了一个令许多哥尼斯堡（德国的一个小城镇Konigsberg）人感到困惑的问题：原来在这座城中有一条河横贯市中心,河中心有两个小岛.在当时有七座桥把这两个小岛和对岸联结起来.见下面的图示：当时有人曾想办法从家里出发走过所有的桥回到家里,他们想是否能够从某座桥出发使得所走过的桥都只过一次呢？许多人都尝试过,但都没有获得成功,那么现在是否有一种办法,能把所有的桥都走过一次呢？欧拉的朋友将这个“哥尼斯堡七桥问题”告诉了欧拉,并且要他想法子解决.欧拉并没有真的去哥尼斯堡,而是把这个问题进行了数学处理：把两岸和两个小岛缩成一点,把桥化为边,两个顶点有边线联结.欧拉得到了下面的图：欧拉考虑这个图能否用一笔画成,如果能够一笔画成的话,则对应的七桥问题也就解决了.为此,欧拉先研究了一般的能一笔画出的图形应该具有什么样的性质？他发现其中的点可以分为两种,全部点都是偶点或者有两个点是奇点（进出点的边数是偶数的点称为偶点；进出点的边数是奇数的点叫奇点）.我们知道,如果一个图能够用一笔画出,那么在这个图上一定有一个点是始点（起笔点）,一个点是终点（收笔点）,其它的点为过路点.首先,我们看过路点具有的性质.在这种点一定是有进有出的,不可能有进无出或者有出无进,即这类点为偶点；其次,考虑始点与终点,并且这两个点不重合的情况,此时它们一定是奇点；再有,始点与终点重合的情况,此时它们也是属于有进有出的点,即为偶点.综上,一个图要是能够一笔画出的话,则其中的点应该有两个奇点,其余的点全部为偶点；或者其中的点都是偶数点.由于七桥问题中的点（4个）都是奇点,所以七桥问题不可能一笔画出.这就是说,一个人要想没有重复地走过7座桥是不可能的.七桥问题是Euler在1736年解决的.一般地,该结论被视为图论历史上的第一个定理.。

数据结构课程设计题目：哥尼斯堡的“七桥问题”院系：班级：学号：姓名：2014-2015年度第1学期哥尼斯堡的“七桥问题”一．题目：哥尼斯堡的“七桥问题”二．设计目标帮助学生熟练掌握图和邻接表的使用，了解利用图能够解决生活中的那些实际问题。

三．问题描述在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。

问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点?四．概要设计1>构建用邻接表存储的图结构体：2> 图的初始化3> 读入并存储一个图G4>图G的深度优先搜索5>检查边的度是否全为偶数五．详细设计（给出算法的伪码描述和流程图）总体操作步骤：流程图设计：主流程图：1>构建用邻接表存储的图结构体：typedef struct {int Visited[MAXV]; /* 顶点标记*/int Edges[MAXV][MAXV]; /* 邻接表*/int VertexN, EdgeN; /* 顶点和边数*/} Graph;2>图的初始化：3>读入并存储一个图G4>图G的深度优先搜索:5>检查边的度是否全为偶数:6>主函数：代码分析：1>图的初始化：void InitializeG ( Graph *G ){int i, j;for (i=0; i<MAXV; i++){for (j=0; j<MAXV; j++)G->Edges[i][j] = 0;G->Visited[i] = 0;}G->VertexN = G->EdgeN = 0;}2>读入并存储一个图G:void ReadG ( Graph *G ){ /* 读入并存储一个图G */int i, V1, V2;scanf("%d %d", &G->VertexN, &G->EdgeN);for (i=0; i<G->EdgeN; i++){scanf("%d %d", &V1, &V2);G->Edges[V1-1][V2-1] = G->Edges[V2-1][V1-1] = 1;}}3>图G的深度优先搜索:void DFS ( Graph *G, int V ){ /* 图G的深度优先搜索*/int W;G->Visited[V] = 1; /* 将访问到的结点进行标记*/for (W=0; W<G->VertexN; W++)if (G->Edges[V][W] && !G->Visited[W])DFS(G, W);}4>检查边的度是否全为偶数:int CheckG ( Graph *G ){ /* 检查边的度是否全为偶数*/int r, i, j;for (i=0; i<G->VertexN; i++){r = 0;for (j=0; j<G->VertexN; j++)r += G->Edges[i][j];if (r%2) return 0; /* 发现奇数度的边则返回0 */}return 1; /* 全是偶数度的边则返回1 */}5>主函数：int main(){int i;Graph *G = malloc( sizeof(Graph) );InitializeG( G );ReadG( G );DFS( G, 0 ); /* 检查连通性*/for (i=0; i<G->VertexN; i++)if (!G->Visited[i])break;if (i<G->VertexN) /* 若有结点没被DFS访问到*/printf("0\n"); /* 则图不连通*/else /* 若图连通*/printf("%d\n", CheckG(G));return 0;}六．测试分析白盒：查看代码完整性黑盒：测试是否可以正确的创建，删除，插入，打印，查找等操作七．使用说明插入删除语句：删除1条内容插入语句：插入一条信息自动打印：打印内容八．测试数据注：学生在测试数据时，需要写出测试用例和截图十．课程设计总结通过“哥尼斯堡的“七桥问题””这个题目，我认识到了图的使用，以及邻接表存储。

第二节哥尼斯堡七桥问题教学目标1.了解哥尼斯堡七桥问题的由来2.理解欧拉解决哥尼斯堡七桥问题的方法3.掌握一笔画问题的步骤教学重点掌握一笔画问题的技巧教学过程一、导入哥尼斯堡七桥问题的由来哥尼斯堡曾是东普鲁士的首府，现称加里宁格勒，在俄罗斯境内。

在第二次是世界大战时，的军警哲理入侵波兰。

后来，苏军也是从此地打进德国的。

所以哥尼斯堡是一座历史名城。

同时，在这里诞生和培养过许多伟大人物。

如著名唯心主义哲学家康德，终生没有离开此城。

在哥尼斯堡城中有一条布勒格尔河，横贯城中。

河有两条支流，一条称新河，一条叫旧河，在城中心汇合成一条主流，在合流的地方中间有一座河心岛，这是城中繁华的商业中心。

由于布勒格尔河的流过，使全城分成为四个地区：岛区、北区、东区和南区。

在布勒格尔河上，架了七座桥，其中五座将河岛与河岸连接起来，另有两座架在二支流上。

这一别致的桥群，吸引了众多的哥尼斯堡居民和游人来此河边散步或去岛上买东西。

早在18世纪，就有人提出这样的问题：“能否在一次散步中每座桥都走一次，而且只能走一次，最后又回到原来的出发点？”这个问题吸引了不少人去思考实验。

事实上，要走遍这七座桥的所有走法共有7！=5040种，要想一一验过，谈何容易。

是否在这5040中走法中存在着一条走遍七座桥而又不重复的路线呢？谁也回答不了。

因而形成了著名的“哥尼斯堡七桥问题”。

二、新授哥尼斯堡七桥问题的解决1735年，有几名大学生写信给当时正在俄国彼得堡科学院任职的天才数学家欧拉，请他帮忙解决。

欧拉并未轻视生活小题，他似乎看到其中隐藏着某种新的数学方法。

经过一年的研究，29岁的欧拉于1736年向彼得堡科学院递交了一份题为《哥尼斯堡的七座桥》的论文，圆满地解决了这一问题，同时开创了数学的一个新分支——图论。

问题的抽象——数学化欧拉是如何将这生活的趣味问题转化为数学问题的呢？又是如何证明要想一次走过这七座桥是不可能的呢？欧拉的方法十分巧妙：他用点A、B、C、D表示哥尼斯堡城的四个地区B（岛区）、C（北区）、A（东区）、D（南区）；七座桥看成这四个点的连线，用f，d，a，c，b，e，g七个数字表示,如图3-1。

简述欧拉的哥尼斯城堡七桥问题及其解答。

（原创实用版）目录1.欧拉的哥尼斯城堡七桥问题2.欧拉的解答方法3.欧拉回路的概念及应用4.欧拉图的定义及性质5.结论正文欧拉的哥尼斯城堡七桥问题是指在 18 世纪的哥尼斯堡城（现属于俄罗斯加里宁格勒），有一条河流穿城而过，形成了两个岛屿。

城市中有七座桥，每个岛屿各有三座桥与其他岛屿相连。

问题在于，如何才能一次走遍所有桥，每座桥只走一次，并最终回到起点。

欧拉在研究这个问题时，提出了一种全新的思维方式。

他将问题抽象为一个图论问题，其中桥梁视为图的边，岛屿视为图的节点。

欧拉通过研究图的性质，发现了一个重要的结论：如果一个图是连通的，且所有顶点的度数都是偶数（除了可能有两个顶点的度数为奇数），那么这个图就可以有一条欧拉回路。

欧拉回路的概念在图论中具有重要意义。

欧拉回路是指在一个图中，通过每条边恰好一次且回到起点的一条回路。

欧拉回路的存在性与图的连通性、顶点的度数等性质密切相关。

根据欧拉的结论，我们可以判断哥尼斯堡城的七桥问题无解。

因为在这个图中，有一个顶点的度数为奇数（即终点），不满足欧拉回路的条件。

欧拉的解答为后来的图论研究奠定了基础，并启发了人们研究更多关于图论的问题。

欧拉图是另一种与欧拉回路相关的概念。

欧拉图是指一个无向图，其中每条边都连接着两个顶点的度数之和为偶数。

欧拉图具有一些有趣的性质，如所有顶点的度数都是偶数，图中不存在奇数长度的环等。

欧拉图的概念对图论的研究和发展起到了重要作用。

总之，欧拉的哥尼斯城堡七桥问题是图论领域的一个经典问题，欧拉通过抽象思维，将问题转化为图论问题，并由此发现了欧拉回路和欧拉图等重要概念。

百科名片1736年29岁的欧拉想圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文，在解答问题的同时，开创了数学的一个新的分支-----图论与几何拓扑。

也由此展开了数学史上的新进程。

问题提出后，很多人对此很感兴趣，纷纷进行试验，但在相当长的时间里，始终未能解决。

七桥问题和欧拉定理。

欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡居民提出的问题，而且得到并证明了更为广泛的有关一笔画的三条结论，人们通常称之为“欧拉定理”。

[编辑本段]故事背景七桥问题七桥问题Seven Bridges Problem 18世纪著名古典数学问题之一。

在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。

问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点？欧拉于1736年研究并解决了此问题，他把问题归结为如下右图的“一笔画”问题，证明上述走法是不可能的。

有关图论研究的热点问题。

18世纪初普鲁士的柯尼斯堡，普雷格尔河流经此镇，奈发夫岛位于河中，共有7座桥横跨河上，把全镇连接起来。

当地居民热衷于一个难题：是否存在一条路线，可不重复地走遍七座桥。

这就是柯尼斯堡七桥问题。

L.欧拉用点表示岛和陆地，两点之间的连线表示连接它们的桥，将河流、小岛和桥简化为一个网络，把七桥问题化成判断连通网络能否一笔画的问题。

他不仅解决了此问题，且给出了连通网络可一笔画的充要条件是它们是连通的，且奇顶点(通过此点弧的条数是奇数)的个数为0至1.当Euler在1736年访问Konigsberg, Prussia(now Kaliningrad Russia)时，他发现当地的市民正从事一项非常有趣的消遣活动。

Konigsberg城中有一条名叫Pregel的河流横经其中，这项有趣的消遣活动是在星期六作一次走过所有七座桥的散步，每座桥只能经过一次而且起点与终点必须是同一地点。

Euler把每一块陆地考虑成一个点，连接两块陆地的桥以线表示著名数学家欧拉。