当前位置：文档之家 › 物探精品课程 第二章 第二节 地震波时距曲线

物探精品课程 第二章 第二节 地震波时距曲线

  • 格式：ppt
  • 大小：1.95 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

地震波理论时距曲线

地震波理论时距曲线

1.时距曲线基本概念2.直达波时距曲线3. 反射波时距曲线4. 折射波时距曲线1. 时距曲线的基本概念在地面激发了地震波后，根据地下介质的结构和波的类型（如直达波、折射波和反射波），地震波将具有不同的传播特点。

为了定量地说明不同类型的波在各种介质结构情况下传播的特点，在地震勘探中主要采用“时距曲线”(时距曲线方程)这个概念。

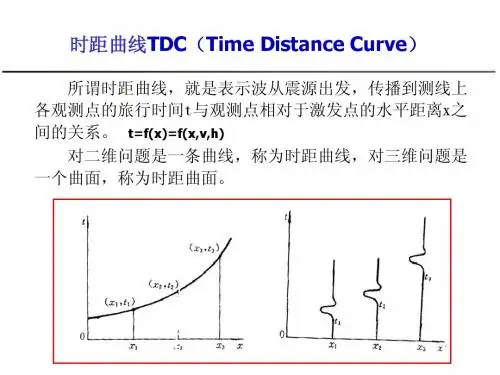
时距曲线：是表示地震波从震源出发，传播到测线上各观测点的旅行时间t，同观测点相对于激发点的水平距离x 之间的关系。

1. 时距曲线的基本概念1.1 时距曲线图a 自激自收，同相轴形态与界面起伏相对应图b 多道接收，同相轴形态与界面起伏不对应1. 时距曲线的基本概念1.2 共炮点和共反射点时距曲线按观测方法的不同分为两种情况：一种是放一炮，在一个多道检波器组成的排列上接收并得到一张地震记录，地下存在反射界面就可以得到相应的反射波时距曲线，称为共炮点反射波时距曲线。

另一种是在许多炮得到的许多张地震记录上，把同属于同一个反射点的道选出来，组成一个共反射点道集，于是可得到界面上某个反射点的共反射点时距曲线。

共炮点记录共反射点记录1.3 几个基本概念•炮检距(offset)：炮点到地面各观测点的距离，也称为偏移距。

•初至时间(first break)：所有波中最先到达检波器(Geophone)并记录下来的地震波第一波峰时间。

•同相轴(event)：各接收点属于同一相位振动的连线。

•共炮点(common shotpoint)：所有接收点具有共同的炮点。

•纵测线(inline)：激发点和观测点在同一条直线上。

•非纵测线(offline)：激发点不在测线上。

1.时距曲线基本概念2.直达波时距曲线3. 反射波时距曲线4. 折射波时距曲线xtxt (x 1,t 1)(x 2,t 2)(x 3,t 3)(x 4,t 4)(x 5,t 5)t10t3t2t4t5x 1x 2x 3x 4x 502. 直达波时距曲线直达波：从震源直接到达检波点的波。

2-1地震波的时距方程与时距曲线

2-1地震波的时距方程与时距曲线

的人组成地震队，工作时间可能几年或十几年。在所研究的 具体对象上也具有明显不同。寻找石油和煤炭的中深层反射 波法勘探，是研究地面以下数百米至数千米的大区域的地质 构造，但是对于近地面1~2百米的地层和较小的构造就难以 精确的定位，达不到工程勘察要求地精度。在找矿勘探中， 由于勘探目标较深，处理地震数据资料时，对于地表面1~2 百米的地层的数据，为了消除干扰和提高地震波信噪比，克 服地表低速层的影响，往往都被切除掉。而浅层反射研究和 应用的区域正是被深层找矿勘探资料处理时切除的部分。浅 层反射这种工作方法，研究地表浅层的构造和地层，要求勘 察的精度高，并能排除表层不均匀和中深层各种各样地震信 号的干扰。因此浅层反射波资料采集处理，难度就较大。这 就构成了工程地震浅层反射法本身的特点。
三）均匀两层介质条件下反射波的时距方程与理论时距曲线 这是一个比较理想化的最简单的地质模型，它表示分界面 两侧的介质都是均匀的。分界面是水平、平界面。 1)建立反射波的时距方程式： 建立反射波的时距方程式： 建立反射波的时距方程式 设两层介质的分界面为R，两侧介质为W1、W2。波阻 设两层介质的分界面为 ，两侧介质为 、 。 不相等。 点激发地震波， 抗Z1和Z2不相等。在O点激发地震波，使用地震检波器，在 和 不相等 点激发地震波 使用地震检波器， 测线上的D1、 、 处接收来自地下分界面R上的 测线上的 、D2、D3…Dn处接收来自地下分界面 上的 、 处接收来自地下分界面 上的A1、 A2、A3…An点的反射波。X1、X2、X3…Xn分别为各道接 点的反射波。 、 、 、 点的反射波 分别为各道接 收点的炮检距。反射波到达各道的时间， 收点的炮检距。反射波到达各道的时间，从地震波的记录图 上可以测量出来。为寻找到X和 t 的函数关系，从图中直接 上可以测量出来。为寻找到 和 的函数关系， 可以看出:： 都是随入射交α的 可以看出 ：OA1、A1D1、OA2、A2D2…都是随入射交 的 、 、 、 都是随入射交 增加而加大，因此比较难以直观、 增加而加大，因此比较难以直观、简单的寻找出 时间 t 和炮 检距X 的函数关系。 检距 的函数关系。

地震波的时距曲线

地震波的时距曲线

正常时差：任一接收点的反射波旅行 时间tX 和同一反射界面的t0之差。
tn t x t0 t0
1 X 2 t0 2V 2
t0
正常时差精确公式有时讨论问题不够直观。在一定的条件下，用二项式展开可以得到简 单的近似公式，以后讨论某些问题时经常用到。
tx t0
1

x2 v2t02
越平缓，曲率越小。
从视速度的角度考虑时距曲线的弯曲情况
视速度定理
t

s v

s' v*
s sin
s'
v* vs' v
s sin
A
△ S‘ B


△ t，△s
由此式可见，视速度一方面反映真速
度，另方面又受传播方向影响，故也 成为识别各种地震波的特征之一。
反射波时距曲线
A工区
B工区
什么情况下直达波的时距离曲线不是直线？
共炮点反射
同一炮点不同接收点 上的反射波，即单炮 记录，也称同炮点道 集。在野外的数据采 集原始记录中，常以 这种记录形式。
可分单边放炮和中间 放炮。
共反射点反射 另一种方式是在许多炮得到的许多张地震记录 上，把同属于某一个反射点的道选出来，组成 一个共反射点道集，于是可得到界面上某个反 射点的共反射点记录。

t0

1


x2 2v2t02
Leabharlann t0x2 2v2t0
x 1 vt0
x2 tn tx t0 2v2t0
结论：
a)、炮检距越大正常时差越大；
b)、反射深度越深正常时差越小；
c)、速度越大正常时差越小。

地震波时距曲线综述

地震波时距曲线综述



在地面激发了地震波后，根据地下介质的结构 和波的类型（如直达波、折射波和反射波）， 地震波将具有不同的传播特点。
4
2019/3/12
一、时距曲线的概念(T-X Curve Conception)

为了定量地说明不同类型的波在各种介质结构 情况下传播的特点，在地震勘探中主要采用 “时距曲线” (时距曲线方程)这个概念。时 间和距离的关系是通过速度联系的。
7
3.
4.
2019/3/12
一、时距曲线的概念(T-X Curve Conception)
单道记录与多道记录
自接 自收 方式 单炮多道 接收方式
多炮 多道 接收 方式
2019/3/12 8
一、时距曲线的概念(T-X Curve Conception)
各种观测方式震源和接收之间的排列
按一定的规律分布称观测系统，在地 震资料采集一章详细描述。 炮检距--激发点到接收点的距离叫炮 检距，也叫偏移距。可有最小炮检距 和最大炮检距。 波传播旅行时--从激发到被接收到所 需的时间即为传播时间
11

2019/3/12
一、时距曲线的概念(T-X Curve Conception)

1 。时距曲线 (T-X Curve)：表示地震波的传播时间 t 和爆炸点与检波点之间的距离x的关系曲线， t-x曲线， 简称时距曲线。 2 。 共 炮 点 时 距 曲 线 Common Shoot Point Time Distance Curve ： 由一点激发，若干接收点接收， 所记录的时距曲线； 3 。共中心点 ( 共反射点 ) 时距曲线 Common Middle Point Time Distance Curve ：炮点与接收点以某一中 心点对称所记录的时距曲线；

工程物探-第二章1理论时距曲线

工程物探-第二章1理论时距曲线

V1
V2 V3
V1
V3
V2
V3 V3
Q KH
H GG
x 2 h1 cos i13 2 h2 cos i23
V3
V1
V2
sin i13
V1 V3
cos i13
V32 V12 V3
sin i23
V2 V3
R2
cos i23
V32 V22 V3
地震勘探 第2章 浅层折射波法和反射波法
2.1 理论时距曲线
地震勘探 第2章 浅层折射波法和反射波法
2.1 理论时距曲线
2.1.2 折射波的时距曲线
1. 水平界面——(3)多层介质
t
x
n1
2
hk
Vn2 Vk2
Vn
k 1
VnVk
如图表示的是五层介质时距
曲线分布图
从图中可以看出：
1> 随着各层波速的逐层增
大，时距曲线的斜率 1 逐
渐减小
Vn
2> 界面越深初至区越远。
2.1.2 折射波的时距曲线
1. 水平界面——(2)三层介质
代入
cos i13 cos i23
V32 V12 V3
V32 V22 V3
t x 2 h1 cos i13 2 h2 cos i23
V3
V1
V2
t x 2 h1 V32 V12 2 h2 V32 V22
V3
V3V1
V3V2
显然也是一条直线
因此引入时 距曲线概念。
地震勘探 第2章 浅层折射波法和反射波法 直达波
反射波
折射波在该点 与反射波相切
折射波
折射波
反射波

2 地震波的时距曲线

2 地震波的时距曲线

当炮检距x小于界面深度H的0.5倍时，这种假设引 起的误差很小;随着炮检距的增大，误差将增大。 从时距曲线的角度来说，意味着在激发点附近由 均方根速度算出的二次双曲线同实际高次时距曲线比 较接近，而远离震源之处则这两支时距曲线差异较大。 在远离震源处时距曲线族中的曲线是相互相交的
三、弯曲界面反射波时距曲线




(2.1.16)
五、多次反射波时距曲线
2.1.7
多次反射波的各种类型
图2.1.-8 界面倾斜时全程二次反射波时距曲线
1．全程多次反射波时距曲线是双曲线，只要两次
利用虚震源原理可以得出多次反射波的时间是从虚 震源出发直接到达各接收点的,其关系见下图；
全程二次反射波相当于在这个假想界面上产生的一 次反射波。显然，根据几何关系，很容易证明：假 想界面的倾角为 2 ，激发点到的法线深度为
sin 2 h 2h cos h sin
把 h′和 ′ 代入一次反射波时距曲线方程，便可 得到全程二次反射波的时距曲线方程
2
t
1 2 sin 2 2 sin 2 2 2 x 4 hx 4 h 2 v sin sin
(2.1.17)
推广到n次全程多次反射波，其时距曲线方程式为
2h cos x tm v
3.倾角时差（界面倾斜引起的单位距离的时间差） 为 t d / x ，
4. 可以根据双曲线极小点的位臵定性地判别界面的倾斜 方向，因为极小点恒位于激发点O的上倾方向一侧。
5.当测线沿界面倾向方向布臵时，视倾角x就是真倾角 ，这时(2-1-6)方程式可写成:
1 t x 2 4h 2 4hx sin v
在震源附近接收时，i角较小，可以略去pvi的高次项

地震勘探-地震波的时距曲线

地震勘探-地震波的时距曲线

2
地震波由震源激发，经过地下岩层反射、折射等 传播路径，被地面检波器接收，形成地震记录。
3
对地震记录进行处理和解释，可以得到地下构造 的图像，为油气勘探和开发提供重要依据。
常用地震勘探方法概述
反射法
利用地震波在地下岩层界面处的反射现象，通过观测反射 波的传播时间和振幅等信息，推断地下岩层的形态和性质 。
供依据。
曲线拟合
根据初至时间和速度信 息，采用合适的数学方 法进行曲线拟合，得到
时距曲线。
质量控制
对绘制的时距曲线进行 质量控制，确保其准确
性和可靠性。
03
地震勘探技术与方法
地震勘探原理简介
1
利用地震波在不同介质中传播速度的差异，通过 观测和分析地震波在地层中的传播规律，推断地 下岩层的性质和形态。
04
时距曲线在地震资料解 释中应用
层位标定与追踪技术
层位标定
利用已知地质信息和钻井资料，将地 震反射层与地质层位进行对应，确定 地震反射层的地质时代和岩性特征。
追踪技术
在地震剖面上，沿着目的层位连续追 踪其反射波，通过反射波的连续性、 振幅、频率等特征，判断层位的横向 变化。
断层识别与描述技术
01
02
数据预处理
对采集到的原始数据进行去噪、滤波 、静校正等预处理操作，提高数据质 量。
03
速度分析
利用预处理后的数据进行速度分析， 得到地下岩层的速度模型。
解释与评价
对偏移成像结果进行解释和评价，识 别地下构造的形态和性质，为油气勘 探和开发提供决策依据。
05
04
偏移成像
基于速度模型对地震数据进行偏移处 理，得到地下构造的偏移成像结果。

第二节一个界面情况下反射波的时距曲线

第二节一个界面情况下反射波的时距曲线

s
0
8h 2
0
t
t
t'
t0 xsin
2xsin
sin
vt d
d
s
s
h
v
2x
由倾角时差估算地层倾角
七、动校正
动校正：
将反射波旅行时,校正到炮检距中点的自激 自收时间 t0m 的过程叫动校正(将反射波旅 行时减去时差得到 x 处的时间。
2
动校正量计算： 1. 平界面:
t 1 v
x2
4h2
t0
MO*2
4h2
xm2
t
1 v
(x xm )2 4h2 xm2
t 1 v
x2 2xxm 4h2
又 xm 2hsin
t 1 x2 4h2 4hxsin
v
倾斜界面反射波时距曲线方程 （上倾方向与x正向一致）。
如上倾方向与x正向相反：
xm
2h s in 得：t
1 v
x2 4h2 4hxsin
直达波时距曲线方程：t x 是一直线。
v
纵测线： 激发点与接收点在同一条直线上，这样的测 线称为纵测线。用纵测线进行观测得到的时 距曲线称为纵时距曲线。 非纵测线： 激发点不在测线上，用非纵测线进行观测 得到的时距曲线称为非纵时距曲线。
除非特别说明，一般都讨论纵时距曲线。
二、水平界面共炮点反射波时距曲线方程
2
t0 1
x2 4h2
2
当x 2h
1时，有：t
t0 1
1 2
x2 4h2
t0 1
x2 2v 2t02
x2 t
2v 2t0
六、倾角时差
界面倾斜时，旅行时 t是由于倾角不为零 引起的时差：t t t0 tn ，界面倾斜，测 线与界面倾向一致 OS OS',tORS tOR'S' ，它们 之差为倾角时差。

第二章1-1理论时距曲线

第二章1-1理论时距曲线

第二章 地震波勘探（第3－6讲）讲授内容：浅层折射波法、反射波法、瑞雷面波法 讲授重点：浅层折射波法和瑞雷面波法 目的要求：要求学生掌握折射波法和面波法。

第一节 浅层折射波法和反射波法地震波传播特征等内容不讲，大家在石油勘探中已经学过了。

折射波法和反射波法在工程勘察中都很有用，但反射波法大家在石油物探中已经学过，故其讲述重点是折射波法，反射波法部分只讲与石油地震勘探不同的地方。

折射波法在工程地球物理勘探中是最古老的方法之一。

反射波法在工程地球物理领域的应用是八十年代中后期的事情。

大家都知道，波在两种不同介质的分界面上会产生反射和透射，当满足波的全反射条件（2V ＞1V ,波的入射角等于临界角）时，会在界面上产生全反射现象，亦即产生折射波。

折射波勘探就是利用这种波在地层中传播的运动学特性来进行地层结构的探测的。

§1－1理论时距曲线问题从理论的时距曲线谈起，在时距曲线上看折射波和反射波的运动学特性。

1.1.1直达波理论时距曲线时距曲线方程： Vxt是一条过原点的直线，其斜率的倒数为表层波速V 。

求出其倒数， 就可以得出地表覆盖层的波速。

1.1.2折射波理论时距曲线 1、水平界面的折射波时距曲线1) 两层介质：利用入射角等于临界角时方能产生折射波的条件，可以求出折射波的时距曲线方程为：12cos 2V ih V x t +=21212222V V V V h V x -+=02t V x+=上式即为两层水平介质的折射波时距曲线方程。

它表示时距曲线是一条直线，其斜率的倒数为 2V 之值。

0t 是0=x 时，时距曲线的截距时间，是时距曲线延长线与t 轴相交处的时间值。

式 0t 2121222V V V V h-= 表示出了界面深度h 和截距时间0t 之间的关系。

当已知1V 和2V 时，可以求得界面的深度h 。

在测线上无法接收到折射波的范围称为盲区。

其大小为：i h x m tan 2=21arcsinV V i =2）三层介质：条件：1)：3V ＞2V ＞1V ，2)：当入射波在2R 界面上的B 点产生折射时，则入射射线在界面处必须满足∠23i =)/arcsin(32V V 和∠13i =)/arcsin(31V V ，即透过1R 界面的角度13i 和2R 界面的临界角23i 间的关系为：322311390sin sin sin V V i V i == 设来自2R 界面的折射波传播时间为3t ，类似于二层结构的求解过程得到：232223213212313322V V V V h V V V V h V x t -+-+=其时距方程仍然为一直线方程，直线斜率的倒数为3V 。

时距曲线

时距曲线

S OSA S O SA OS O S , OA O A
* *
*
波由O 入射到A 再反射回S 点所走过的路 程就好象由点直接传播到S 点一样，在地 震勘探中，把这种讨论地震波反射路径的 简便作图方法称为虚震源原理。
O* S 1 2 1 2 2 2 t x (2h0 ) x 4h0 v v v
由震源出发向外传播，没有遇到分界面直接 到达接收点的波叫直达波。一个纵波入射到 反射面时 ，即产生反射纵波和反射横波，也 产生透射纵波和透射横波。与入射波类型相 同的反射波或透射波称为同类波。改变了类 型的反射波或透射波称为转换波。入射角不 大，转换波很小，垂直入射不产生转换波。
㈢按波所能传播的空间范围： 体波：
1 2h x 4hx sin x x 4h 4hx sin 1 , 当 1时 v v 4h 2h x 4hx sin t t 1 8h x 4hx sin t t 1 , t 为O点处自激自收时间 8h t x sin 2 x sin vt t t t sin h v 2x
纵波和横波可以在介质的整个立体空间 中传播，合称为体波。
面波：
沿自由表面或分界面传播的波叫面波。其 强度随离开界面的距离加大而迅速衰减。
R
2v2 1v1 2v2 1v1
R：反射系数（由介质1入射到分界面时界
面的反射系数）。
在界面产生反射波条件：分界面两边介 质的波阻抗不相等。 波阻抗界面才是反射界面，速度界面不 一定是反射界面。 进行反射波法地震勘探时（目前主要利用反 射纵波），习惯上把这种被我们利用的波称 为有效波，妨碍记录有效波的其它波都称为 干扰波。

第二部分 地震勘探333

第二部分 地震勘探333
折射波时距曲线
折射波时距曲线
已知折射波时距曲线和直达波时距曲线求界面 上下地层的速度和界面的深度： 1 . 求 上 部 地 层 的 速 度 V1 2. 求 下 部 地 层 的 速 度 V2 3 . 求 交 叉 时 t i， 利 用 下 式 计 算 界 面 深 度 ： V1 s in θ c = V2 cos θ c = 1 − s in 2 θ c V1t i h = 2 cos θ c
h
V
x
t5 t4 t3 t2 t1 0 x1 x2 x3x4 x5 x 0
反射界面R
反射波时距曲线
如图示：界面R 埋深h 波速为V 如图示：界面R，埋深h，波速为V
OA+ AS 2 2 X 2 1 t= = h + ( ) = 4h2 + X 2 2 V V V 上式即反射波时距方程， 上式即反射波时距方程，是一个 关于X的二次方程， 关于X的二次方程，化简得 t2 X2 − =1 2 2 ( 2h V ) ( 2h)
>> X2
时，即2h
>> X时，二项式展开，略高次项 二项式展开，
1 X2 1 X2 2 X2 ∆tn = t0 [1+ ( 2 2 ) − ( 2 2 ) + ⋯] − t0 ≈ 2 2 2 t0 V 8 t0 V 2t0 V
上式表明， 上式表明 ， 正常时差可用抛物函 数逼近。 正常时差校正（ 数逼近 。 正常时差校正 （ 动校正 ） ： 把各点时间减去相应正常时 都变成t0时间 差，都变成 时间
视速度定理
视速度： 视速度：时距曲线沿测线变化率的倒数 dt OA + AS 2 走时曲线斜率 k = dX t= =
V
Va = dX 2h = V 1+ ( )2 dt X

地震勘探地震波的时距曲线

地震勘探地震波的时距曲线

tn t x t0 t0
1 X 2 t0 2V 2
t0
tx t0
1
x2 v2t02

t0

1


x2 2v2t02



t0

x2 2v2t0
tn

tx
t0

x2 2v2t0
结：
a)、炮检距越大正常时差越大；
b)、反射深度越深正常时差越小；
c)、速度越大正常时差越小。
4、正常时差(NMO, Normal MoveOut)
t0时间：时距曲线在t轴上的截距： t0

2h V
表示波沿界面法线传播的双程旅行时间，自激自收时间。
t
X 2 ( 2h)2 V2 V
X2 V2
t02
t0
1 X 2 t0 2V 2
正常时差：任一接收点的反射波旅 行时间tX 和同一反射界面的双程垂 直时间t0之差。
时距曲线的弯曲情况
对两个界面：
深层反射波返回地表的α角比浅层的要小 (α深＜α浅)，Va相对变大，斜率变小，曲 线变缓，则深层的时距曲线比浅层平缓。
反射界面埋藏越深，反射波时距曲线越平 缓，反正，则越陡！！
时距曲线的弯曲情况
曲率大
曲率小
4、倾斜界面的反射波时距曲线
1．反射波时距方程
R为倾斜界面，倾角为 ，界面 以上波速为V。 先求取时距方程。为讨论简便， 采用镜象法。
视速度定理：
t OA AS 2
V
V
h2
(X
2)2
1 V
4h2 X 2
Va

dX dt
V

地震勘探-地震波的时距曲线共112页

地震勘探-地震波的时距曲线共112页
16、云无心以出岫，鸟倦飞而知还。 17、童孺纵行歌，斑白欢游诣。 18、福不虚至，祸不易来。 19、久在樊笼里，复得返自然。 20、羁鸟恋旧林，池鱼思故渊。
地震勘探-地震波的时距曲线
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪ቤተ መጻሕፍቲ ባይዱ
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
112

地震勘探原理__各章要点总结

地震勘探原理__各章要点总结

第一章 地震勘探的理论基础1、各向同性介质：弹性与空间方向无明确关系的介质称各向同性介质，否则是各向异性介质。

2、泊松比σ：弹性体受力纵向伸长(缩短)与横向收缩(膨胀)的比值。

L L d d //∆∆=σ3、对于大多数沉积岩石，σ=0.25，∴V P =1.73V S 。

4、瑞雷面波(R 波)特点：(1) 波的能量分布在地表附近的介质中并随深度迅速衰减。

(2) 质点振动方向分上、下、坐、右，合成的振幅轨迹是椭圆(逆时针方向)，长轴垂直地面，长短轴比值是2/3。

(3) 当σ=0.25时，V R = 0.92V S =0.54V P ，速度低、频率低(10~30Hz)，波形宽。

(4) 有频散(波散)现象，不同频率的成分传播速度(相速度)不同，即群速度不等于相速度。

5、拉夫面波(L 波) 特点：能量沿地震界面分布，振动方向与传播方向垂直，振动平面平行界面，即为SH 波，由于水平振动，检波器接收不到。

6、地震波的特征：运动学特征——研究波在地层中传播的空间位置与传播时间的关系。

动力学特征——研究波在地层中传播的能量(振幅)变化和波形特征(频谱)。

7、惠更斯原理(1690)也叫波前原理，说明波向前传播的规律。

在弹性介质中，任意时刻波前面上的每一点，都可看作是一个新的波源(子波)而产生二次扰动，新波前的位置可认为是该时刻各子波波前的包络。

惠更斯原理只给出了波传播的空间位置，而不能给出波传播的物理状态。

菲涅尔(1814)对惠更斯原理进行了补充：波在传播时，任意点处的振动，相当于上一时刻波前面上全部新震源产生的子波在该点处相互干涉的合成波。

8、视速度定理地震波的传播是沿射线方向进行的，而观测地震波是沿测线方向进行的，其方向和射线方向不一致。

波前沿测线传播的速度不是真速度V ，而是视速度*V 。

αsin //=∆∆=∆∆∆∆=*xs t x t s V V βαcos sin V V V ==* 式中 α——射线与地面法线的夹角，称入射角；β——波前与地面法线的夹角，称出射角。

物探--7地震时距曲线、野外工作处理解释

物探--7地震时距曲线、野外工作处理解释

线，其斜率为1/v2,延长线与T轴 的交点称交叉时，与界面的法
向深度有关。
三、折射波时距曲线
下面我们来看一下直达 波、折射波、反射波 之间的关系：
三种波在时距曲线上
A
到达时间是不同的
盲
B
反射波法勘探应在 A点以内观测；
区
折射波法勘探应在 B点以外观测。
四、绕射波时距曲线
地层中，当存在断层、直立地层的棱角、地层尖灭点等 不连续点时，可以产生绕射现象。（狭义绕射）
下面我们简单介绍反射波法地震资料的采集、处理和解释。
一、地震资料采集 1、测线布置与观测系统
地震测线的布置一般要求与构造走向垂直。 地震测线一般为直线，有时为折线或弧线，随地质条件
而定。地震测线分为纵测线和非纵测线。见图。 在二维地震测量中，常采用纵测线。 在三维地震测量中，常采用纵测线
和非纵测线同时并用。
多次波：地震波遇到波阻抗分界面时，除产生一次 反射外，还会产生一些来往于分界面之间几次反 射的波，这种波称为多次反射波。
多次波的类型：全程多次反射 波、短程多次反射波、微曲多
次反射波、虚反射。
二、多次反射波时距曲线
只有在反射系数较大的反射界面产生的多次反射， 才能够形成较强的多次波。
这样的界面有：基岩面、不整合 面、火成岩面、低速带底界面、 海水面和海底面等。
面波（也叫地滚波ground roll）:低频、强振幅、低速， 野外可用检波器排列压制。
工业电干扰（50Hz）：陷波压制。
多次波(multiples)：与初次反射有同样的速度，可利用 预测反褶积消除。
边部散射波(side-scattered noise):水底不平，散射点
不对称
平
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


2 zu V1
cosi
根据视速度定理有
(2-10) (2-11)
代入(2-11)式得
T *
V1
d sin i
(2-12)
t x
d
Td* t0d
(2-13)
图2-13 折射波相遇时距曲线图
第二节 地震波时距曲线
同样方法亦可得到O2激发，O2O1区间接收时的时距曲线方程：
式中
tu

在图2-12中，我们还可以看到直达波、折射波和反射波三者之间的关系, 这为选择最佳观测段提供了依据。
第二节 地震波时距曲线
四、绕射波和多次反射波时距曲线
1．绕射波
地震波在传播过程中，当遇到断层的
棱角、地层尖灭点、不整合面的突起点
或侵入体如上所述，绕射波将以这些点
为新震源向周围传播。如图2-19所示，
点)左侧时，上式取负号。
由方程可见,该时距曲线为一条过原点O的直线，该直线斜率的倒数即为
V*。即
V * x / t
(2.2.2)
当忽略震源深度时，一般可近似认为V*等于表层层速度V1。其时距曲线
参见图 2-12所示。显然，在一定观测范围内，直达波最先到达接收点。
第二节 地震波时距曲线
2、折射波时距曲线
若以T=t2，X=x2为变量作图，式(2-19)变成斜率为和截距为的直线，如图2-17
所示。利用这一关系可确定反射界面之上地层的速度值V。
根据反射波时距曲线方程式(2-17)，可求得沿测线变化的视速度：
V*

dx dt
V
1 4H2 x2
(2-20)
分析式(2-20)可以看出，在爆炸点附近(x→0)，V趋于无穷大，而在无穷远处
第二节 地震波时距曲线
一、直达波与折射波时距曲线
1、直达波时距曲线
所谓直达波即是从震源点出发后经反射或折射以速度V直接传播到各接收
点的地震波。当震源位于地表附近,并采用纵测线观测时,其时距曲线方程为
：
t x /V*
(2.2.1)
其中V*为波沿测线传播的视速度，x为传播距离。当接收点在原点(激发
n
t2
li
n
2
hi
V i1 i
i1 Vi cos i
(2-27)
式中：li是每一层中波传播的路径长度；是波在每一层中的入射
角，i=1，2，…，n。 其中
称为均方根速度。
V


n
tiVi 2
i1
n
1/
2


ti
i1

(2-28)
第二节 地震波时距曲线
的倒数等于界面速度。
图2-12 直达波和一个水平层的 折射波、反射波时距曲线
第二节 地震波时距曲线
由图2-12可见,时距曲线的D点为折射波的始点,D
点内无折射波，为折射波的盲区，D点以外，折射
波先于反射波到达接收点，且在一定范围外，也
先于直达波到达接收点。
（2）倾斜折射层
如图2-13所示，倾斜折射层倾角为，在O1、O2
从激发点O发出的入射波到达绕射点A，
然后以绕射波形式到达地面的任意观测
点D,显然,波的旅行时是由两部分组成：
第一部分，入射波旅行OA所需的时间
t AO 1
1
V1
V1
L2 h2
(2-29)
图2-19 绕射波及其时距曲线
第二节 地震波时距曲线
另一部分是绕射波经过AD的传播时间
t AD 1
倾O2接收与下倾O2激发、上倾O1处接收时波的旅行路径一样，满足互换原
理，旅行时间T相等，T称作互换时间。
第二节 地震波时距曲线
（3）弯曲界面的折射波时距曲线 折射界面不一定都是平面，可能是凹凸不平的曲面，界面倾角不是常量。
从式(2-12)或(2-15) 很容易看出倾角 变化，V*随之变化，增大，V*变小，
(x→∞)，视速度趋近于真速度。视速度变化的原因是由于反射波在各观测点
处的出射角不同。另外，还可以得出：反射界面埋藏越深，视速度越大，时
距曲线越平缓。
任一观测点P的反射波旅行时t和同一反射界面的双程垂直时间t0的差，定义
为正常时差，即
t t t0
x V
2 t02 t0
当炮检距x与深度H的比很小(即
x Vt0
<<1)时，正常时差根据下式给出：
t x2 2V 2t0
(2-21 )
第二节 地震波时距曲线
对同一反射层而言，当V和t0为常数时，正常时差t与炮检距平
方x2成正比。鉴于这个道理,在浅层高分辨率地震反射勘探中， 为解决近炮点处接收到的浅层反射波正常时差小、不易准确求 取速度的问题，常采用扩展排列接收，求取地层速度。使用正 常时差可判断地震记录上的同相轴是正常的反射波，还是强于 扰背景条件下接收到的相于干扰波等噪声；共深度点叠加前需 要消除正常时差，正常时差也是速度分析的基础。
倾斜的界面，改变上述式中 的符号，可得出相应的时距关系
式。当地震勘探测线的走向与地层倾向不一致时，如测线走向
与地层倾向有夹角 时，则地层的真倾角 与视倾角 x不等。
容易证明，地层的真倾角 、视倾角 x 与 之间的关系为：
sin cos sin x
(2-24)
当 =0°时，表示测线沿地层倾向布置，此时视倾角 x 等于真
x Vd*
t0u
(2-14)
t
Tu* sin
2zd
0u
V1
V1
i
cos
i
（2-15） （2-16）
相应的两条时距曲线如图2-13所示，二者都是直线，互相交叉，称为相
遇时距曲线。这两支时距曲线斜率不同，下倾方向接收视速度小，时距曲线
陡；上倾方向接收视速度大，时距曲线平缓，另外，由于上倾O1激发，在下
目录
第二节 地震波时距曲线
一、直达波与折射波时距曲线 二、单界面反射波时距曲线 三、水平层状介质反射波时距曲线 四、绕射波和多次反射波时距曲线
第二节 地震波时距曲线
在地震勘探中，观测的测线为在地面或井中的直线 ，一般情况下震源的位置与测线在一条直线上。此时 ，时间场函数t=(x，y，z)对于测线而言变为了一个二 维问题t=t(x，z)，而对于测线上某一测点而言就变为了 一个一维问题t=t(x)或t=t(z)，此时，场点坐标与波至时 间的时距关系由时距曲而变为了时距曲线。可见所谓 时距曲线即是测线上各接收点坐标与波至时间的关系 曲线。由此，我们只需要讨论各种波的时距曲线特征 ，即可获得正演问题的解。
xm 2H sin
tm

2H cos V
界面倾角越大，xm的绝对值就越大。
第二节 地震波时距曲线
图2-18 一个倾斜界面反射波时距曲线
第二节 地震波时距曲线
在界面倾斜情况下，地层界面倾角 可正可负，视所选测线的
坐标方向与界面倾斜情况的相对关系来决定。若地层上倾方向
与x轴正方向一致，取负号，反之取正号。因此，对于相反方向

OS V

1 V
x xm 2 zm2

1 V
x2 4H 2 4Hxsin
(2-22)
或
t2 2H cos
2

x 2H sin 2 2H cos 2
1
V
(2-23)
可以看出，反射波的时距曲线也是双曲线，但对称轴不是时间轴。双曲线的顶点偏
向界面上倾方向，据此特点可判别反射界面倾斜方向。类似地，当x=0时，为自激自 收条件下的反射时间。时距曲线极小点的坐标为
倾角 ；当 =90°时,表示测线沿地层走向布置，此时 x =0 。
第二节 地震波时距曲线
当测线沿地层倾向布置时， x = 。对式(2-22)作二项式展开，并略去
高次项得：
t

t0
1
x2 4Hxsin 8H 2
求地层倾角 的最简单方法是根据震源两边等距的两个观测点的旅行时
（1）单一水平折射层
设地下有任一水平折射层，具深度为z，下
伏介质速度V2大于上覆介质波速V1，入射
波以临界角i投射到界面R上，在平坦的地
面观测，如图2-12。根据波传播路径，可得
时距曲线方程为：
t cosi OM MP PG4
V1
V2
V1
x 2 ztgi
2z
x 2z
2
V1
V2
x L 2 h2
(2-30)
26)求真倾角。此外，倾角时差与 x成正比，为提高测量倾角的精度，应
尽可能采用较大的x值。
第二节 地震波时距曲线
三、水平层状介质反射波时距曲线
设有一组水平层状介质，在O点激发，在S点接收，第i层的
速度和厚度分别为Vi和 hi，如图2-19所示。第n层底界面反射波 到达S点的传播时间为通付各层的传播时间总和，即
在浅层地震反射波法勘探中，由于浅层界面的反射波时距曲线陡，而深 层的反射波时距曲线平缓，所以在远炮检距处，深、浅层的反射波时距曲线 可能相交，而在近炮检距处不相交，这就决定了在浅层地震反射勘探中常采 用近炮点处接收。此外，由图2-12可见，为避免折射波的干扰，应选择在折 射盲区范围内观测。反之，若要进行折射波法勘探，则应在盲区范围以外进 行观测。
方程，曲线对称于时间轴。渐近线是t=x/V(
直达波时距曲线)。当x=0时， t0

2H V
为自激
自收的反射时间，根据t0可确定反射层的埋
深H：
H

1 2
Vt0
式(2-17)也可写成：
(2-18)