第三节康普顿效应及其解释(精)

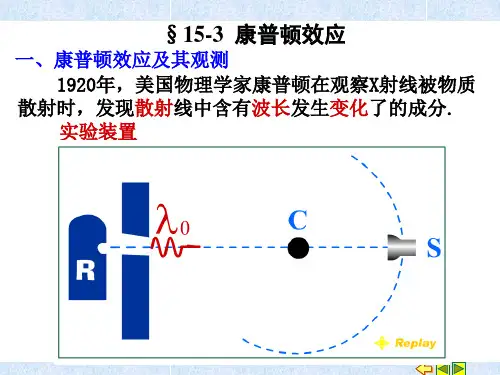
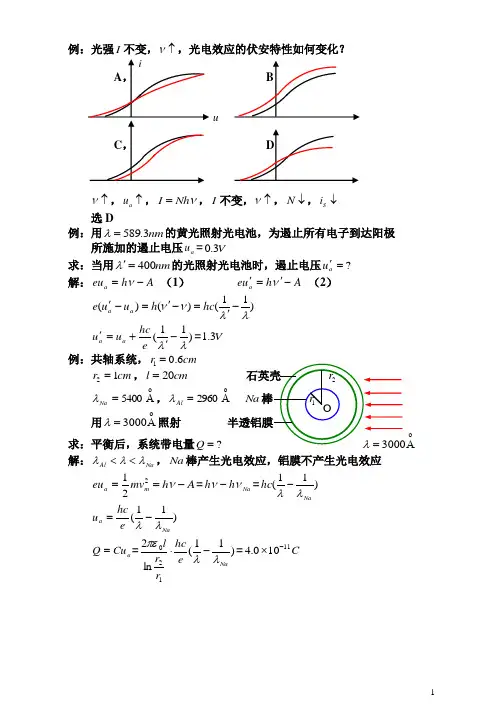
1例：光强I 不变，↑ν，光电效应的伏安特性如何变化？u↑ν，↑a u ，νNh I =，I 不变，↑ν，↓N ，↓S i选D例：用nm 3.589=λ的黄光照射光电池，为遏止所有电子到达阳极 所施加的遏止电压a u =V 3.0求：当用nm 400='λ的光照射光电池时，遏止电压?='au 解：A h eu a -=ν （1） A h u e a-'='ν （2） )11()()(λλνν-'=-'=-'hc h u u e a a)11(λλ-'+='e hc u u a a=V 3.1 例：共轴系统，cm r 6.01=cm r 12=，cm l 20= A=5400Na λ，A =2960Al λ Na 用A =3000λ照射 求：平衡后，系统带电量?=QA 解：Na Al λλλ<<，Na 棒产生光电效应，铝膜不产生光电效应221m a mv eu =A h -=ν=Na h h νν-=)11(Na hc λλ- )11(Naa e hc u λλ-=a Cu Q ==)11(ln 2120Na e hc r r l λλπε-⋅=C 11100.4-⨯2第3节 康普顿效应（1） 光致发光（2）光电效应（3）康普顿效应（4）产生正负电子对光子能量增加 一、 实验规律φ：散射角1、∀φ ∃两种散射x 射线⎩⎨⎧λ>λλ=λ康普顿散射瑞利散射::002、对于康普顿散射0λλ>波长改变量)(0φλλλf =-=∆，↑φ，↑∆λ λ∆与散射体物质种类无关，与0λ无关3、康普顿散射的相对强度与散射体的原子量有关 原子量较大，康普顿散射相对较弱 原子量较小，康普顿散射相对较强 二、 经典解释带电粒子的振动频率=入射电磁波的频率=辐射电磁波的频率 三、 光量子理论对康普顿效应的解释散射过程是光子与散射体中电子弹性碰撞，动量守恒，能量守恒 光子与自由电子碰撞，光子能量↓，↓ν，↑λ：康普顿散射光子与束缚较紧的电子碰撞，光子能量不变，波长不变：瑞利散射 原子量较小时，几乎每一个电子都可视为自由电子 康普顿散射相对较强原子量较大时，原子核对内层电子束缚较紧，只是 对外层电子束缚较弱，康普顿散射相对较弱动量守恒：00n h λ=e P n h +λ， 00n h λe P n h=-λ能量守恒：=+00E hc λE hc +λ， -0λhc E E hc =+0λ20222202cos 2eP h h h =-+φλλλλ，220222222022cos 2e P c c h c h c h =-+φλλλλ222022000022222222)(22e P c E E E E hchcc h c h c h +==+-+-+λλλλλλ2mc E =3=-)cos 1(2022φλλc h 200)(2c m hchc λ-λ=2000)(2c m hc λλλλ- 2sin 2)cos 1(2000φφλλλc m h c m h =-=-=∆令cm h c 0=λ， 2s i n 220φλλλλc=-=∆ c m hc 0=λ= A =⨯⨯⨯⨯--024.01031011.91063.683134：电子的康普顿波长 2πφ=，c c λφλλ==∆2sin 22c λ：垂直入射线方向上散射x 射线的波长改变量20c m hc =λ，c cm h λλ==0 c λ：能量等于电子静止能量的光子的波长↑φ，↑∆λ，πφ≤≤0，c λλ20≤∆≤ 0=φ，0=∆λ，πφ=，c λλ2=∆λ∆仅与φ角有关，与散射体物质种类无关，与0λ无关例：用A =20.00λ的x 射线与自由电子碰撞， 在 90=φ方向观察x 射线 求：（1）散射x 射线的波长（2）反冲电子的动能 （3）反冲电子的动量解：（1）2πφ=，c c λλλλλ==-=∆2sin 220A =+=+=224.0024.020.00c λλλ（2）=+00E hcλE hc +λ，J hc hc E E E k 15001007.1-⨯=-=-=λλ （3）00n h λ=e P n h +λ， 00n h P e λ=n h λ-，222022λλh h P e +=22011λλ+=h P e =1231044.4--⨯kgms224.02.0//00===λλλλθh h tg ， 8.41=θ4 例：对于康普顿效应，证明ννννφ002022)(2sin h c m -=动量守恒：00n c h ν=e P n ch+ν， 00n h νe P c n h =-ν 能量守恒：=+00E h νE h +ν， -0νh E E h =+0ν220222202cos 2e P c h h h =-+φνννν222020*********)(22e P c E E E h h h h h +=+ν-ν+νν-ν+ν=-)cos 1(202φννh 200)(2c m h νν- ννννφ002022)(2sin h c m -=第4节 氢原子光谱 玻尔理论一、 氢原子光谱422-=n n B λ，∞=,,5,4,3 nA =7.3645B αH βH γH ∞H∞→n ，B =∞λ巴耳末系，∞H ：线系极限B =∞λ=A 7.3645：线系极限波长波数ν~：沿波线单位长度内波的个数 cνλν==1~λ )121()121(4)41(1411~2222222nR n B n B n n B -=-=-=-==λν ,5,4,3=n里德伯公式1710096776.14-⨯==m BR ：里德伯恒量帕邢系：)131(1~22n R -==λν， ,6,5,4=n 2mc E =c。

第三节 康普顿效应及其解释
课前预习
情景导入
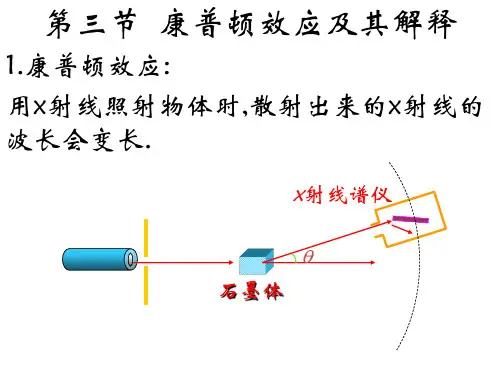
1922年，美国物理学家康普顿在研究石墨中的电子对X 射线的散射时发现，有些散射波的波长比入射波的波长略大，他认为这是光子和电子碰撞时，光子的一些能量转移给了电子（图2-3-1）.康普顿假设光子和电子、质子这样的实物粒子一样，不仅具有能量，也具有动量，碰撞过程中能量守恒，动量也守恒.按照这个思想列出方程后求出了散射前后的波长差，结果跟实验数据完全相符，这样就证实了他的假设.这个现象叫做康普顿效应
.
图2-3-1
问题：你能根据所学知识进行解释吗？
简答：光子与电子发生碰撞遵循动量守恒定律和能量守恒定律，碰撞后，电子获得了动能，而光子的能量减少，故光子的频率也变小.
知识预览
⎪⎪⎪⎪⎪⎩
⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧==动量守恒和能量守恒光子与粒子的碰撞遵循光子动量光子能量光子说顿效应由磁理论无法解释康普解释提出由美国物理学家康普顿变长散射出去的射线的波长射线照射物体时当现象应效顿普康λh P hv E X .,:。

2.3 康普顿效应及其解释课堂互动三点剖析对康普顿效应的理解（1）经典解释（电磁波的解释）单色电磁波作用于比波长尺寸小的带电粒子上时，引起受迫振动，向各方向辐射同频率的电磁波.经典理论解释频率不变的一般散射可以，但对康普顿效应不能作出合理解释！ （2）光子理论解释X 射线为一些E=hν的光子，与自由电子发生完全弹性碰撞，电子获得一部分能量，散射的光子能量减小，频率减小，波长变长.这个过程设动量守恒与能量守恒仍成立，则由电子：p=m 0v;E=2021v m (设电子开始静止，势能忽略)；光子：p=h/λ;E=hν=h·λc，由以上几式得：λ-λ0=2sin 220θ-c m h . 其中（h/m 0c ）=2.34×10-12m 称为康普顿波长.如图2-3-2图2-3-2各个击破【例题】 在康普顿散射中，入射光子波长为0.03οA ，反冲电子的速度为0.6c,求散射光子的波长及散射角.解析：反冲电子的能量增量为ΔE=mc 2-m 0c 2=2206.01-c m -m 0c 2=0.25 m 0c 2由能量守恒定律，电子增加的能量等于光子损失的能量，故有λλhchc-=0.25m 0c 2散射光子波长λ==-00025.0λλc m h h 1083134103410030.0103101.925.01063.610030.01063.6-----⨯⨯⨯⨯⨯⨯-⨯⨯⨯⨯=4.3×10-12m=0.043οA由康普顿散射公式，Δλ=λ-λ0=2sin 220ϕc m h =2×0.024 3sin 22ϕ可得sin20243.02030.0043.02⨯-=ϕ=0.267 5，散射角为φ=62°17′. 答案：0.043οA 62°17′类题演练证明康普顿散射实验中，波长为λ0的一个光子与质量为m 0的静止电子碰撞后，电子的反冲角θ与光子散射角φ之间的关系为tanθ=100)]2tan()1[(-+ϕλc m h . 解析：将动量守恒式写成分量形式mvsinφ-)(λhsinφ=0① mvcosθ+)(λhcosφ=λh② 及康普顿效应结论：λ-λ0=2sin 220ϕc m h ③由①②得 tanθ=ϕλλϕcos )(sin 0-上式分子为 sinφ=2sin )21cos()21(ϕϕ 分母为 ϕλλλλϕλλcos )(cos )(000--+=- 将③代入 0λλ-cosφ=2sin 200)2(λϕc m h +·2sin 2)2(ϕ=2sin 2)1(200λϕc m h + 所以tanθ=100)]2tan()1[(-+ϕλc m h .。