当前位置：文档之家 › 3-1-1 应力状态分析

3-1-1 应力状态分析

  • 格式：pdf
  • 大小：371.23 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

基础3-1(地基应力和沉降)

基础3-1(地基应力和沉降)
� Nhomakorabea�
� �
在地下水位以下，如埋藏有不透水层 (例如岩层或只含 结合水的坚硬粘土层 )，由于不透水层中不存在水的浮 力，所以层面及层面以下的自重应力应按上覆土层的 水土总重计算。 自然界中的天然土层，一般形成至今已有很长的地质 年代，它在自重作用下的变形早巳稳定。但对于近期 沉积或堆积的土层，应考虑它在自重应力作用下的变 形。 此外，地下水位的升降或大面积人工填土会引起土中 自重应力的变化 (书45页图3.3)。 例如在软土地区，常因大量抽取地下水，以致地下水 位长期大幅度下降，使地基中原水位以下的有效自重 应力增加，而造成地表大面积下沉的严重后果。至于 地下水位的长时期上升，常发生在人工抬高蓄水水位 地区 (如筑坝蓄水 )或工业用水大量渗入地下的地区， 如果该地区土层具有遇水后发生湿陷的性质，必须引 起注意。
程，各种土随着荷载大小等条件的不同， 其所需时间的差别很大，关于地基变形随 时间而增长的过程是土力学中固结理论的 研究内容。它是本章的一个重要组成部分。
� 土中应力计算常采用弹性理论求解，即 假
� 假定和工程实际的一些分析 � 一、关于连续性问题 � 土是由三相物质组成的具有孔隙的非连续
定地基土是均匀、连续、各向同性的半无 限空间线弹性变形体。 � 实际土体是层状、非均质、各向异性的材 料。 � 作这种假定可简化计算，实践表明，在应 力不大的情况下，假定做出的计算结果与 工程实际非常接近，能够满足实际工程的 要求。
� 地基的沉降，必须要从土的应力与应变的
� 地基土的变形都有一个由开始到稳定的过
基本关系出发来研究。 � 对于地基土的应力一般要考虑基底附加应 力、地基自重应力和地基附加应力。 � 地基应力一般包括由土自重引起的自重应 力和由建筑物引起的附加应力，这两种应 力的产生条件不相同，计算方法也有很大 差别。 � 此外，以常规方法计算由建筑物引起的地 基附加应力时，事先确定基础底面的压力 分布是不可缺少的条件。

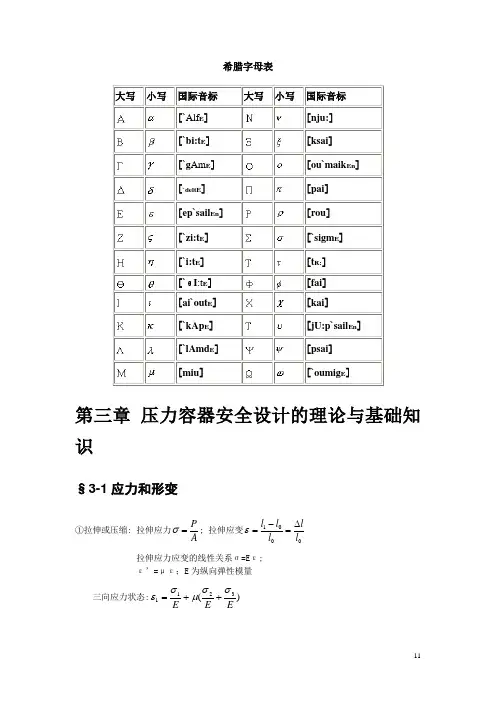
第3章 压力容器安全设计的理论与基础知识1

第3章 压力容器安全设计的理论与基础知识1

希腊字母表第三章 压力容器安全设计的理论与基础知识§3-1应力和形变①拉伸或压缩: 拉伸应力A P =σ; 拉伸应变0001l l l l l ∆=-=ε 拉伸应力应变的线性关系ζ=E ε;ε’=με；E 为纵向弹性模量三向应力状态:)(3211EEEσσμσε++=)(3122EEEσσμσε++=)(2133EEEσσμσε++=②剪切时：剪切应力AP =τ; 剪切应变h a tg ==γγ剪切应力应变的线性关系η=G γ;)1(2μ+=EG ，为剪切弹性模量③弯曲时 (平面弯曲) ：平面弯曲应力 JMy=σ 其中yJ 为横截面对中性轴的惯性距dF y F⎰=2； 不同形状的截面，惯性矩J 是不同的。

例如圆形截面对中性轴的惯性矩为644d π（d 为圆直径），矩形截面对中性轴的惯性矩J 为123bh （b 为矩形宽，h 为矩形高），从这里也可以看出，即使是截面尺寸相同的矩形，扁放和立放时的惯性矩也是不一样的。

曲率半径EJM ==ρ1§3-2容器的薄膜应力压力容器按厚度可以分为薄壁容器和厚壁容器。

通常是将容器的厚度与其最大截面圆的内径之比小于0. 1，即外径/内径≤1.2者为薄壁容器，超过这一范围的容器称为厚壁容器。

薄壁容器的弯曲变形在壳壁上引起的应力要比拉伸压缩引起的应力小的多，可忽略。

这种理论称为薄膜理论或无力距理论。

如图3-2所示的圆筒形容器，当其受到内压力p 作用以后，其直径要略微增大，故筒壁内的"环向纤维"要伸长，因此在筒体的纵向截面上必定有应力产生，此应力称为环向应力， 以ζθ表示。

由于筒壁很薄，可以认为环向应力沿厚度均匀分布。

鉴于容器两端是封闭的，在受到内压力p 作用后，筒体的"纵向纤维"也要伸长，则在筒体的横向截面上也必定有应力产生，此应力称为经向（轴向）应力，以ζm 表示。

本节将通过对回转壳体的应力分析，推导出任意轴对称回转壳体的应力计算公式。

应力状态例题(整合全部)

应力状态例题(整合全部)
N B 56.6 k N
A
45
B
得：
q
2m
XA YA NB B
（2）选择等边角钢型号
N B 56.6 103 2 A 353 . 75 mm [ ] 160 106
查附录Ⅲ
A q
选择40 5角钢， 其横截面面积为379.1mm 2
拉伸与压缩/拉（压）时的强度计算 例题4 应力 图示结构，钢杆1：圆形截面，直径d=16 mm,许用
F
b

F
L
L
材料力学
剪切实用计算
解：剪切面如图所示。剪
F/2 F
切面面积为：
A Lb
由剪切强度条件：
剪切面
F/2
Fs F / 2 [ ] A Lb
由挤压强度条件：
F L 100mm 2b[ j ]
jy
Fb F /2 [ jy ] A jy b
材料力学


0.022 160 106
由平衡条件：
M
A
0
[ F ] AB [ FN ] ADsin
[ FN ] ADsin 50.24 1 0.75 / 0.752 1 12.06 kN [F ] 2 .5 AB
拉伸与压缩/轴向拉（压）时的变形 C 0.75m A 1m D D
[ ]1 150MPa ；杆2：方形截面，边长 a=100 mm, [ ]2 4.5MPa ,(1)当作用在B点的载荷 F=2 吨时，校核强 度；(2)求在B点处所 1.5m 能 承受的许用载荷。 B A 1 解： 一般步骤：
2m F 外力 内力 应力
2
C
利用强度条 件校核强度

构造地质学(3)地质构造分析的力学基础

构造地质学(3)地质构造分析的力学基础
• 屈服
• 屈服点
• 屈服极限
• 岩石在断裂前塑性变形应变达5—8%为中等韧性，超 过10%的材料性质为韧性，而脆性材料在弹性变形阶 段后，和断裂变形阶段前就没有或只有极小的塑性变 形（3—5%）
塑性变形的显微机制
• 由于岩石类型、围压条件、温度、应变速率和施加应力类型的不同，出现脆性到韧性的一系列变化现象， 在压缩和拉伸条件下，其变化有五种情况。
2. 剪应变： （1）定义：
角应变：变形前相互垂直的两条直线， 变形后其夹角偏离直角的量（ψ）
剪应变：角应变的正切（ γ ） （2）应变量计算：γ= tgψ
（右偏为正；左偏为负）
应变轴的规定及与主应力轴之关系
• 通过变形物体内部任意点总可以截取这样一个 立方体，在其三个互相垂直的面上都只有线应 变而无剪应变，即只有伸长和缩短，这三个互 相垂直的面称为主应变面，三个主应变方向称 为主应变轴。并规定：最大伸长方向为最大应 变轴（A轴），最大缩短方向为最小应变轴（C 轴），介于两者之间为中间应变轴（B轴），B 轴方向既可是拉伸，也可以是缩短
3.2 变形分析
•3.2.1 变形和应变
• 物体受到力的作用后，其内部各点间相互位置 发生改变，称为变形。变形可以是体积的改变， 也可以是形状的改变，或二者均有改变。
• 物体变形的程度用应变来量度，即以其相对变 形来量度，应变所涉及的物体形态的变化，总 是与物体的两个状况有关—初态和始态，所以 下面所指的应变，只涉及到系统的两个特定的 状态。
A.平移；B.旋转；C.形变；D.体变
物体变形的泥巴实验
Brittle Deformation Ductile Deformation
M.S. Patterson
Fig. 10.7

3 复合材料的设计原理和复合理论

3 复合材料的设计原理和复合理论

3复合材料的设计原理和复合理论3．1 概述材料设计是指根据对材料性能的要求而进行的材料获得方法与工程途径的规划。

对设计一词的传统解释为：进行某项制作或工程以前，根据该项目的使用目的和性能要求，拟定其材料、结构、工艺、用地、进度、费用等各方面的计划和估算。

在传统设计中，材料仅仅处于在市场上可以提供的范围内被选择的地位。

当一种材料被设计人员选定后，设计的任务仅仅是确定其构件的几何尺寸。

例如设计一个承受内外压差P（由于外压通常为一个大气压，一般远小于压力容器的额定内压，此处P往往取为内压）的一定直径的圆筒，只需根据其受力来计算其壁厚t（见图3-1）。

由管壁取出单元体进行力学分析。

因管壁的径向应力较小可略去不计，按平面应力状态来计算，即仅考虑周向应力σc和轴向应力σa。

图3-1 承受内压p圆筒的应力分析由材料力学的知识知，周向力的平衡为：2σc tΔl = p dΔl轴向力的平衡为：p(πd2/4) =σaπdt由以上二式可以分别求出管壁所受的周向应力σc和轴向应力σa为：σc = pd /(2t)（3-1）σa = pd /(4t) （3-2）可见：σc= 2σa（3-3）令σc≤[σ],据此决定圆筒的壁厚t，则t ≥pd /(2[σ ])（3-4）其中,t为壁厚；d为圆筒的直径；[σ]为所选材料的许用应力，一般由材料手册查得。

公式（3-3）说明危险将出现于周向，但是，如果按照式（3-4）来设计，则轴向的强度储备过多，对于各向同性材料，这种浪费是无法避免的。

传统设计的流程（或步骤）可以归纳为:选取材料→查取其[σ]值→确定壁厚t→计算重量→确定加工方法→计算成本复合材料设计是通过改变原材料体系、比例、配置和复合工艺类型及参数，来改变复合材料的性能，特别是使其具有各向异性，从而适应在不同位置、不同方向和不同环境条件下的使用要求。

复合材料的可设计性赋予了结构设计者更大的自由度，从而有可能设计出能够充分发掘与应用材料潜力的优化结构。

应力状态概述二向和三向应力状态的实例二向

应力状态概述二向和三向应力状态的实例二向

力等。
决定材料强度和稳定性
02
应力状态对材料的强度和稳定性有重要影响，是评估材料能否
承受外力作用的关键因素。
指导结构设计
03
了解应力状态有助于合理设计结构，优化材料使用，提高结构
的稳定性和安全性。
应力状态的应用
机械和航空航天领域
在机械和航空航天领域，应力状态分析用于评估各种设备和结构 的强度、疲劳寿命和稳定性。
应力状态概述
目录
• 引言 • 二向应力状态 • 三向应力状态 • 结论
01
引言
定义与概念
定义
应力状态是指物体在单位面积上所承 受的内力分布情况，用于描述物体在 受力作用下的状态。
概念
应力状态由主应力、剪应力和应变等 参数描述，这些参数反映了物体在受 力作用下的变形和破坏趋势。
应力状态的重要性
二向应力状态的实例
平板受压
当一个平板受到垂直于其平面的均匀 压力时，其内部的应力状态即为二向 应力状态。此时，平板受到两个相互 垂直的主应力作用，第三个应力分量 等于零。
圆柱形压力容器
当一个圆柱形压力容器受到均匀压力 时，其侧壁的应力状态为二向应力状 态。此时，侧壁受到两个相互垂直的 主应力作用，第三个应力分量等于零。
平面应变状态
平面应变状态的描述
当一个物体受到的应变分量都作用在同一个平面内时，称 该物体处于平面应变状态。
平面应变状态的特性
在平面应变状态下，只有两个相互垂直的主应变分量，而 第三个应变分量等于零。这种状态通常出现在受到均匀压 力或均匀拉伸的薄壁结构中。
平面应变状态的应用
在岩土工程和材料科学中，平面应变状态是常见的。例如， 在土壤力学中，土壤的压缩和膨胀分析需要考虑平面应变 状态。

3-1-4 应力分析_应力莫尔圆及应力平衡微分方程

3-1-4 应力分析_应力莫尔圆及应力平衡微分方程

10 3 10
l1=
10 1
m2= 10
最大切应力τmax=500MPa
金属塑性成形原理
解析法验证：
2 3 0
三个不变量： J1 x y z 4
J2
(x y
yz
zx )
2 xy
2 yz
2 zx
21
ij 3
0
6 0(100MPa) 0 0
J3
x
y z
2 xy
yz zx
( x
金属塑性成形原理
练习题1： 应用莫尔圆分析单向拉伸时的各横截面上的应力变化状态。
y B（ σy＝40 τyx＝0 ） θ
τ C (0,20)
2θ
A
A
（ σx＝0 τxy＝0 ）
Bσ
(40,0)
x
当2θ＝90°（θ＝45°）时，截面的剪切力 达到最大值20MPa
金属塑性成形原理
练习题2：物体中某点为平面应力状态，应力张量为：
试利用莫尔圆图解主应力,主方向和最大切应力
τ
τmax (0,5)
2 3 0
ij 3 6 0(100MPa)
0 0 0
2α2
B(6,3)
σ2 (-3,0) 2β2
A(-2,-3) σ2＝－3
2α1 σ1(7,0)
O(2,0) D
σ
2β1 σ1＝7
OD的长度＝1/2（6+2）＝4；R＝5；
y
B
以应力主轴为坐标轴，作一斜微分面，其方向
余弦为l，m，n，则有 :
金属塑性成形原理
l2 m2 n2 1
S1 1 l S2 2 m S3 3 n S 2 S12 S22 S32 12l 2 22m2 32n2

工程塑性力学-屈服准则

工程塑性力学-屈服准则

Mohr-Coulomb 准则
Drucker-Prager 准则
Rankine 准则
1876 年，Rankine提出：一点的最大主应力 达到拉伸强度时，材料发生拉伸破坏。 用于确定脆性材料是否会发生拉伸破坏。 可用来判断混凝土拉伸开裂的起因。 屈服面：拉伸破坏面
1
max(1 , 2 , 3 ) ft ft 由简单拉伸试验确定。
2
那么Tresca准则变为：
xx yy 2 xy k 2
2
即

xx
yy 4
2 2 xy
2 s
上式分别代入yy = -s , 0, s，得到xx-xy 平面 上的屈服轨迹。
xy
xx
Mises 屈服准则
轴向拉伸试验：
1 s , 2 3 0
1 3 s , 2 0
s k 2
k s
纯剪试验：薄壁圆筒扭转试验
1 s s 2
s 与 s 均可由试验测定，常用钢材的试验 结果与上式不完全符合，说明Tresca屈服准则 是近似正确的。
Tresca准则是分段线性的，简化计算；适用 于主方向已知且不变的情况下；
Mises 、 Tresca 准则分别对应于材料力学中 的第三、第四强度理论。
例3：闭端薄壁圆筒受内压 p 的作用，理想 塑性材料，屈服极限为s = 245 GPa。 用Mises、Tresca准则求最大许可的内压 p。 解：首先确定危险 点的应力状态（远离 封头的筒身位置）：
Drucker-Prager 准则
1952 年提出，是对 Mises 准则的修正，它考 虑了静水压力对屈服的影响：

土力学第3章

土力学第3章

第3章土中应力计算3.1概述土体在荷载的作用下，发生沉降、倾斜和水平位移。

如果应力变化引起的变形量在容许范围内，则不会对建筑物的使用和安全造成危害，当外荷载在土中引起的应力过大时，会导致建筑物产生过量变形而影响其正常和安全使用，甚至会使土体发生整体破坏而失去稳定。

而对建筑物地基基础进行沉降(变形)、承载力与稳定分析，都必须掌握建筑前后土中应力的分布和变化情况。

实际工程中土体的应力主要包括土体本身自重产生的自重应力及由外荷载引起的附加应力。

3.1.1应力计算的有关假定(1)连续体假定，是指整个物体所占据的空间都被介质所填满不留任何空隙。

土是由颗粒堆积而成的具有孔隙的非连续体，因此在研究土体内部微观受力情况时(如颗粒之间的接触力和颗粒的相对位移)，必须把土当成散粒状的三相体来看待；但当我们研究宏观土体的受力问题时，土体的尺寸远大于土颗粒的尺寸，就可以把土体当作连续体对待。

(2)完全弹性体假定，是指应力与应变呈线性正比关系，且应力卸除后变形可以完全恢复。

根据土样的单轴压缩试验资料，当应力很小时，土的应力-应变关系曲线就不是一条直线，如图3-1所示，亦即土的变形具有明显的非线性特征。

而且在应力卸除后，应变也不能完全恢复。

但在实际工程中土中应力水平较低，土的应力-应变关系接近于线性关系，可以用弹性理论方法。

但是对一些十分重要、对沉降有特殊要求的建筑物或特别大的重型而复杂的工程，用弹性理论进行土体中的应力分析就可能精度不够，这时必须借助土的更复杂的应力-应变关系和力学原理才能得到比较符合实际的应力与变形解答。

(3)均质假定，是指受力体各点的性质是相同的。

天然地基土是由成层土组成的，因此将土体视为均质将会产生一定的误差，不过当各层土的性质相差不大时，将土作为均质体所引起的误差不大。

(4)各向同性假定，主要是指受力体在同一点处的各个方向上性质相同。

天然地基土往往由成层土所组成，可能具有复杂的构造，而且，即使是同一成层土，其变形性质也随深度而变，地基土的非均质很显著，因此将土体视为各向同性也会带来误差。

连续介质力学第三章(分析“应力”文档)共110张PPT

连续介质力学第三章(分析“应力”文档)共110张PPT
一点的应变状态可用二阶张量的形式来表示，称为 应变张量，用表示，即：
x xy xz
ij
y
yz
=
(对称)
z
x
1 2
xy
y
(对称 )
u
x
1 2
u y
v x
1 2
u z
w x
=
v y
1 2
v z
w y
(对称)
w
z
1
2 1
2
xz yz
z
◆ 几何方程：
x
u x
；
y
v y
性体变，从而出现奇异屈服面。
⑩.平衡（或运动）微分方程
◆ 平衡微分方程：
x
x
yx
y
zx
z
F
x 0
2u t2
xy
x
y
y
zy
z
F
y
0
2v t2
xz
x
yz
y
z
z
F
z 0
2w t2
ij'j Fi 0
◆ 一个客观的弹性力学问题，在物体体内任意一点的 应力分量和体力分量必定满足这组方程。
xxyssii n n xyycco o s sq q00sci on s xy
(xyq0)ctg (xyq0) tg
yxtan
左边界：据圣文南原理和平衡的原理得：
Fx 0 , Fy 0 , M0 0 ,
h
hxdy 0
h
hxydy P0
h
h x ydy M 0
h xdy 0
理论上可证明：当一点的应力状态确定时，经推导 必可求出三个实根，即为主应力，且主应力彼此正交。

应力状态分析和强度理论

应力状态分析和强度理论

03
弹性极限
材料在弹性范围内所能承受的最大应力状态，当超过这一极限时，材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时，其内部应力状态会发生变化，当达到某一特定应力状态时，材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态，当超过这一极限时，材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服（即非弹性变形）的应力状态，是材料强度分析的重要依据。
根据不同的材料特性，存在多种屈服条件，如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示，用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据，当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时，材料会发生屈服和塑性变形，导致失效。该准则适用于韧性材料的失效分析，尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环，主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线，并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响，因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。

3-1-2 应力分析_主应力与主切应力

3-1-2 应力分析_主应力与主切应力

J1 x y z 15
J2
( x y
yz
z
x
)
2 xy
2 yz
2 zx
60
J3
x
y z
2 xy
yz zx
( x
2 yz
2
y zx
z
2 xy
)
54
金属塑性成形原理
将J1、J2和J3代入应力状态特征方程（式3-15） 主应力：
3 15 2 60 54 0 ( 9)( 2 6 6) 0
σ1 = σ2 = σ3 球应力状态。所有方向都没有剪应力，所以都是主方向
而且所有方向的应力都相等。
σ1
σ1
σ1
σ1
σ2 σ3
σ2 σ3
σ2
σ3
σ2
主应力表示的各种应力状态
金属塑性成形原理
主应力图：
一点的应力状态可用作用在单元体上的主应力来描述，只用主应力 的个数及符号来描述一点的应力状态的简图称为主应力图。
2 6
3 ,m3
2 6
3 ,n3
1 3
金属塑性成形原理
二、应力张量不变量
利用应力张量的三个不变量J1、J2、J3 ，可以辨别应力状态是否相同
J11 x y z a b
J
1 2
( x y
y z
z x
)
2 xy
2 yz
2 zx
ab
J
1 3
x
y z
2
xy
yz zx
( x
2 yz
金属塑性成形原理
3-1-2：应力分析 ——主应力与主切应力
内容提纲
一、主应力 二、应力张量不变量 三、应力椭球面 四、主切应力和最大切应力

机械设计考研练习题-机械零件的强度

机械设计考研练习题-机械零件的强度

机械零件的强度一 名词解释(1) 静应力：静应力:大小和方向不随转移而产生变化或变化较缓慢的应力，其作用下零件可能产生静断裂或过大的塑性变形，即应按静强度进行计算。

(2) 变应力：大小和方向均可能随时间转移产生变化者，它可以是由变载荷引起的，也可能因静载荷产生(如电动机重量给梁带来的弯曲应力)变应力作用的零件主要发生疲劳失效。

(3) 工作应力：用计算载荷按材料力学基本公式求得作用在零件剖面上的内力:F c p ,,σσσ　,T,ττ等。

(4) 计算应力：根据零件危险断面的复杂应力状态，按适当的强度理论确定的，有相当破坏作用的应力。

(5) 极限应力：根据材料性质及应力种类用试件试验得到的机械性能失效时应力极限值，常分为用光滑试件进行试验得到的材料极限应力及用零件试验得到的零件的极限应力。

(6) 许用应力：设计零件时，按相应强度准则、计算应力允许达到的最大值ca S σσσ>=]/[][lim 。

(7) 计算安全系数：零件 (材料)的极限应力与计算应力的比值ca ca S σσ/lim =，以衡量安全程度。

(8) 安全系数许用值：根据零件重要程度及计算方法精确度给出设计零件安全程度的许用范围][S ，力求][S S ca >。

二 选择题(1) 零件受对称循环应力时，对于塑性材料应取 Ｃ 作为材料的极限。

A. 材料的抗拉强度B. 材料的屈服极限C. 材料的疲劳极限D. 屈服极限除以安全系数。

(2) 零件的截面形状一定时，当截面尺寸增大，其疲劳极限将随之 Ｃ 。

A. 增高B. 不变C. 降低(3) 在载荷几何形状相同的条件下，钢制零件间的接触应力 Ｃ 铸铁零件间的接触应力。

A. 小于B. 等于C. 大于(4) 两零件的材料和几何尺寸都不相同，以曲面接触受载时，两者的接触应力值 Ａ 。

A. 相等B. 不相等C. 是否相等与材料和几何尺寸有关(5) 在图3-1所示某试件的a m σσ-，极限应力简图中，如工作应力点M 所在的ON 线与横轴间夹角45=θ°，则该试件受的是 Ｃ 。

第2章-2.2(3-1)2012-3-12(2学时-实)

第2章-2.2(3-1)2012-3-12(2学时-实)

第2章2.1 应力的概念及变形体在一点处的应力状态第2.1节应力状态的概念一点各方位截面上的应力的集合称为该点的应力状态。

M 点的应力状态。

一点的应力状态{}n n n n n =1,2,,0lim ,A F p A στ∆→⎧⎫⎛⎞∆⎪⎪==∞⎜⎟⎨⎬∆⎪⎪⎝⎠⎩⎭应力状态分析各方位截面上应力存在内在联系，寻求该关系的过程称为应力状态分析。

pστMniF 2F应力状态的概念应力张量的概念{}n n n n ,n =1,2,,στ0lim ,A F p A ∆→⎧⎫⎛⎞∆⎪⎪==∞⎜⎟⎨⎬∆⎪⎪⎝⎠⎩⎭一点处的应力与其集度以及ΔA 的法向相关,因此可用两个并在一起的矢量表示，这在数学上称为张量。

a bn 0lim A F A∆∆∆→ 描述变形体内部某点的应力状态应用二阶张量描述物理量的类型标量，矢量，张量：2阶张量——应力，应变，n 阶张量转动惯量pστMniF 2F应力的重要概念应力的点的概念一般情形,杆件横截面上不同点的应力不相同。

应力的面的概念一般情形,过同一点不同方位截面上的应力不相同。

应力状态的概念一点处所有各方向面上的应力的集合称为该点的应力状态。

引言2.1.2 应力张量的表示方法单元体的概念取一包围该点的微元体（单元体）其各棱边相互垂直，沿坐标轴方向，各棱边的长分别为d x ，d y ，d z单元体是变形体的最基本研究对象单元体——变形体内某点处取出的边长无限小的体积微元在直角坐标系中，单元体一般取为无限小正六面体zxyMiF nF 2F 1F zxy应力状态的描述单元体每个截面上，都有该点在该截面上的应力矢量（总应力）每个总应力矢量可分解为三个分量zxy 各应力分量的记法:xyσ作用方向yx σyy σyzσ两脚标相同—正应力两脚标不同—切应力zyσzzσzx σσxxxyσxzσMiF 2F 1F nF zxy 由于单元体的尺寸可无限小，通常认为：每个截面上的应力均匀分布；单元体内相互平行截面上的应力相等，方向相反。

材料力学应力状态分析和强度理论

材料力学应力状态分析和强度理论

材料力学应力状态分析和强度理论材料力学是一门研究物质内部各个部分之间的相互作用关系的科学。

在材料力学中，应力状态分析和强度理论是非常重要的概念和方法，用来描述和分析材料的力学行为和变形性能。

材料的应力状态是指在外力作用下，物体内部各个部分所受到的力的分布情况。

应力有三个分量：法向应力、剪应力和旋转应力。

法向应力是垂直于物体表面的作用力，剪应力是平行于物体表面的作用力，旋转应力则是物体受到扭转力产生的应力分量。

应力状态的描述可以用应力矢量来表示。

应力状态分析的目的是确定材料内部各个部分的应力分布情况，进而推导出物体的变形和破坏行为。

常用的应力状态分析方法有平面应力问题、平面应变问题和三维应力问题。

平面应力问题是指在一个平面上的应变为零，而垂直于该平面的应力不为零；平面应变问题是指在一个平面上的变形为零，而垂直于该平面的应力不为零；三维应力问题则是指在空间中3个方向的应力都不为零。

强度理论是指根据材料的内部应力状态来评估其抗拉强度、抗压强度和抗剪强度等，以判断材料是否能够承受外力而不发生破坏。

常见的强度理论有最大正应力理论、最大剪应力理论和最大扭转应力理论。

最大正应力理论是指在材料的任何一个点，其法向应力都不能超过材料的抗拉强度；最大剪应力理论则是指剪应力不能超过材料的抗剪强度；最大扭转应力理论则是指旋转应力不能超过材料的极限扭转强度。

实际应用中，强度理论通常与材料的断裂理论结合起来，以评估材料的破坏行为。

材料断裂的主要原因是应力超过了材料的强度极限，从而导致材料的破坏。

为了提高材料的强度和抗拉性能，可以通过选择合适的材料、改变材料的结构和制造工艺等方法来实现。

综上所述，材料力学应力状态分析和强度理论是描述和分析材料力学行为和变形性能的重要理论和方法。

通过深入研究应力状态、应力分析和强度理论，可以为材料的设计和制造提供指导和支持，从而提高材料的强度和抗拉性能。

3-1-3 应力分析_应力偏张量及等效应力

3-1-3 应力分析_应力偏张量及等效应力
2. 等效应力在数值上等于单向均匀拉伸（或压缩） 应力σ1 ，即： 1
3. 等效应力不代表某一实际表面上的应力，因而不能在某一特定平面上表 示出来。
4. 等效应力可以理解为代表一点应力状态中应力偏张量的综合作用。
等效应力是研究塑性变形的一个重要概念，与材料的塑性变形有 密切关系的参数。
金属塑性成形原理
应力张量的分解
σz τ τ zx zy
τyz
= τxz τxy τyx σy
σx
σm
σm +
σm
a) 任意坐标系
σ3
σm
'
τzx
τzzy τyz
'
τxz τxy τyx y
' x
' 3
σ2 =
σ1 应力张量
σm +
' 2
σm
' 1
b) 主轴坐标系
应力球张量
应力偏张量
金属塑性成形原理
2 zx
1 6
[(
x
y )2
(
y
z )2
(
z
x)2
6(
2 xy
2 yz
2
zx
)]
J 3
x y z
2 xy yz zx
( x
2 yz
y
2 zx
z
2 xy )
对于主轴坐标系：
J1 0
J 2 J 3
1 [(1
6
1 2 3
2 )2
(
2
3 )2
(
3
1)2
]
应力偏张量用来表示不同的变形类型。如J1=0，表明应力偏张量已不含 平均应力成分； J2与屈服准则有关；J3决定了应变的类型：J3>0属伸长类应 变，J3=0属平面应变，J3<0属压缩类应变。

应力状态与应变状态分析

应力状态与应变状态分析
概念
应变状态分析对应力状态分析起到补充作用，特别是在复杂受力情况下，能够更 准确地描述物体的变形行为。
应变状态的分类
单轴应变
物体在单向受力过程中发 生的应变，只有一个方向 的长度变化。
双轴应变
物体在双向受力过程中发 生的应变，长度变化发生 在两个相互垂直的方向上。
三轴应变
物体在三向受力过程中发 生的应变，长度变化发生 在三个相互垂直的方向上。
塑性变形
在某些高应力状态下，材料可能 会发生塑性变形，影响其机械性 能和稳定性。
断裂韧性
材料的断裂韧性可能会受到其内 部应力的影响，高应力状态可能 降低材料的断裂韧性，导致材料 更容易断裂。
02
应变状态分析
定义与概念
定义
应变状态分析是研究物体在受力过程中内部应变的分布和变化情况，以及应变与 应力之间的关系。
详细描述
在塑性行为下，材料发生屈服，即应力达到某一特定值后，应变开始急剧增加。这种行为通常发生在 材料承受的应力高于其屈曲点时。
脆性行为
总结词
当材料受到外力作用时，它可能会突然断裂，而不会发生显著的形变。
详细描述
在脆性行为下，材料在较低的应力状态下就会断裂，且断裂前几乎没有明显的塑性变形。这种行为常见于某些脆 性材料，如玻璃或陶瓷。
弹性行为
总结词
当材料受到外力作用时，会发生形变， 但当外力去除后，材料能够完全恢复 其原始形状和尺寸。
详细描述
在弹性行为下，材料的应力和应变之 间呈线性关系，即应力与应变成正比。 这种行为通常发生在材料承受的应力 低于其屈服点时。
塑性行为
总结词
当材料受到外力作用时，会发生形变，并且当外力去除后，材料不能完全恢复其原始形状和尺寸。

三轴试验应力123大小关系

三轴试验应力123大小关系

三轴试验应力123大小关系
【原创实用版】
目录
1.三轴试验简介
2.三轴应力试验的应力大小关系
3.结论
正文
一、三轴试验简介
三轴试验是一种广泛应用于岩土工程、材料科学等领域的实验方法，主要用于研究材料在三个正交方向上的应力状态。

三轴试验能够模拟实际工程中材料的应力状态，为工程设计和施工提供重要依据。

在三轴试验中，通常需要测试三个主应力（σx, σy, σz）的大小关系，以评估材料的强度和稳定性。

二、三轴应力试验的应力大小关系
在三轴试验中，三个主应力（σx, σy, σz）之间的关系可以通过实验数据进行分析。

根据实验结果，可以得出以下结论：
1.在大多数情况下，σx > σy > σz。

这是因为在多数材料中，x 方向的拉伸强度最大，y 方向次之，z 方向最小。

2.当材料受到横向压缩时，σy 可能大于σx。

这种情况下，材料的稳定性会受到影响，可能导致侧向挤压或剪切破坏。

3.当材料受到竖向压缩时，σz 可能大于σx 和σy。

这种情况下，材料容易发生挤压破坏。

4.在某些特殊情况下，三个主应力的大小关系可能发生变化，例如在复合材料、功能梯度材料等特殊材料中。

三、结论
综上所述，通过分析三轴应力试验的应力大小关系，可以对材料的强度和稳定性进行评估。

在实际工程中，根据材料的应力状态，可以采取相应的设计和施工措施，以确保工程安全和稳定。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
13．1．4．1 任意坐标系
设ABC为主平面，在主平面上有τ=0 由于τ2= S2-σ2 即可得S=σ 所以Sx=Sl=σl Sy=σm Sz=σn 因此有： (σx-σ)l+τyxm+τzxn =0
τxyl+(σy-σ)m+τzyn =0 τxzl+τyzm+(σz-σ)n=0 而：l2+m2+n2=1 此为隐含条件 所以有：
第13章 应力分析stress analysis
本章内容：应用塑性力学分析金属在外力作用下的变形行为 本章重点：点的应力状态分析
应力stress：单位面积上的内力。
材料力学方法：切面法，将物体切开, 利用内力外力平衡条件求切面上 的应力分布。
：把物体切成无数个微六面体（或其他形状），称微元体或单元体，根据 单元体静力平衡条件写出平衡微分方程，再考虑其他条件求解。
13．1 应力状态分析
目标：任意一点的应力状态stress state —— 整个变形体的应 力状态
13．1．1 应力分析截面法
外力outside forces—— 产生内力 应力：正应力（stress）σ，切应力（shear stress）τ 要点：截开物体后，内力变外力。 13．1．1．1 单向拉伸uniaxial tensile应力分析
13．1．4．2 主轴坐标系
若以主应力（σ1 σ2 σ3方向即主轴方向）作坐标系，则坐标轴 为1，2，ห้องสมุดไป่ตู้方向轴。
此时， 在此坐标系下的任意斜面（l, m, n）上有：
S1=σ1l S2=σ2m S3=σ3n 以及：S2=σ12 l2+ σ22 m2 +σ32n2
σ=σ1 l2+ σ2 m2 +σ3n2 τ2= S2-σ2 而且：J1=σ1 + σ2 +σ3 J2=-(σ1σ2 + σ2σ3 +σ3σ1) J3=σ1σ2σ3 又由于：l2+m2+n2=1 所以有： 此方程为一椭球面方程，称应力椭球面。 其中S1 S2 S3分别表示全应力S在1，2，3轴向上的投影。
σ1）2]/6 J3/ =σ1，σ2，σ3，
作用：根据应力偏张量判断变形类型
J3/ >0伸长， J3/ <0压缩， J3/=0平面应变 在三向静水压力下金属如何变形？
习题： 13章 4、8
4、应力偏张量和应力球张量的物理意义是什么？ 8、已知受力体内一点的应力张量分别为
MPa, MPa, MPa, （1）画出该点的应力单元体 （2）求出该点的主应力及主方向、主切应力、最大切应力、等效应 力。 （3）画出该点的应力莫尔圆。
因此σij=是对称张量 当同一单元取不同坐标系时，各应力值会不一样，但是点 的应力状态未改变。 圆柱坐标 ——柱坐标应力张量 球坐标——球坐标应力张量
13．1．3 任意斜面上的应力stress on the oblique plane
已知应力状态σij=，求斜面ABC上的应力（全应力 S，正应力σ，切应力τ）,设斜面ABC的法线方向 余弦为l, m, n 即：
将σ1=20代入求 l1 m1 n1 有方程组： （10-σ1）l+0×m-10n=0 0×l+(-10-σ1)m+0×n=0
-10×l+0×m+（10-σ1）n=0 且有：l2+m2+n2=1
可求出：l1 = -n1= ± m1=0 同理代入σ2=0 可求出l2 = n2=± m2=0
σ3=-10可求出l3 = n3=0 m3=±1 实际上解本题：将对称阵经正交变换转变为对角阵，且求 正交变换，即：
已知，求 使
练习：Mpa，求主应力及主方向。
13．1．5 主切应力和最大切应力maximum shear stress
cipal shear stress——当切应力为极大值时，注意：此时正应力不一定为0。 推导：取应力主轴作为坐标轴 τ2= S2-σ2 =σ12 l2+ σ22 m2 +σ32n2-（σ1 l2+ σ2 m2 +σ3n2） 求τ的极值 且条件为l2+m2+n2=1 解出三个极值为： l=0 m=± n=± 此时τ23=±（σ2 -σ3）/2 此面上有σ=（σ2 +σ3）/2 l=± m=0 n=± 此时τ31=±（σ3–σ1）/2
2）三应力同时增减同值时，主切应力值不变。
13．1．6 应力球张量与应力偏张量spherical tensor of
stress and deviator tensor of stress
13．1．6．1 应力张量的分解
σij= 应力偏张量 应力球张量 其中：σm=(σx+σy+σz)/3=J1/3
特点：应力偏张量使形状变化，应力球张量使体积变化 结论：材料的塑性变形由应力偏张量引起。
13．1．6．2 应力偏张量性质
应力偏张量有三个不变量J1/ J2/ J3/ 其中J1/=0 J2/ 和J3/ 的表达式与前述类似。
在主坐标系中有： J1/=0 J2/ =[（σ1 –σ2）2+（σ2 -σ3）2+（σ3 –
习题： 13章 1、7
1、什么叫张量？张量有什么性质？ 7、已知受力物体内一点的应力张量为Mpa，求外法线方向余弦为的斜 切面上的全应力、正应力和切应力。
13．1．4 主应力与应力不变量stress invariants
主平面principal plane——切应力为0的平面。 主应力principal stress——主平面上的正应力。 应力主轴（主方向）——主平面的法线方向。 也就是将 变换为，即将实对称阵变为对角阵。
C1面上全应力：S=F/A=F/(A0/cosθ)=σ0 cosθ 正应力：σ=Scosθ=σ0 cos2θ 切应力：τ=Ssinθ=σ0 cosθsinθ
结论：任意方向都可由σ0 和θ确定其全应力S，正应力σ，切应 力τ，即：单向拉伸只需σ0即可确定任意面的应力状 态。
13．1．1．2 两向应力状态 设任意斜面AB（夹角θ）上的全应力S， S可以分解为正应力σ，切应力τ
满足条件：连续，均质，同性，平衡，无体积力，体积不变。 可列方程：平衡微分方程（平衡，3个）， 几何方程（连续均质，6个）， 物理方程（应力应变关系，6个） 屈服准则 （ 1个） （共16个）
：坐标x, y, z, 位移u, v, w, 应力6个，应变6个。
力的类型有 面力：作用力，反作用力，摩擦力 体积力：重力，磁力，惯性力——高速成形不能忽略
概念： 单向应力状态——两个主应力为0 平面应力状态——一个主应力为0
可以分别写出单向应力状态和平面应力状态的应力张量
13．1．4．3 解例
例题：Mpa，求主应力及主方向 解：方法1，可以求J1 J2 J3，然后求解。
方法2，用 即 行变换后 即 再列变换有
所以：σ1=20，σ2=0，σ3=-10 注意：σ1 σ2 σ3按大小顺序排列。
此面上有σ=（σ1 +σ3）/2 l=± m=± n=0 此时τ12=±（σ1 –σ2）/2
此面上有σ=（σ1 +σ2）/2 若σ1>σ2 >σ3则τmax=（σ1 –σ3）/2
此切应力为最大值即最大切应力。 主切应力平面
特性：1）三向等拉等压状态σ1=σ2 =σ3=±σ，则 τ12=τ23=τ13=0
返回目录
l=cos(N, x) m=cos(N, y) n=cos(N, z)
解：将全应力沿坐标方向分解为：Sx Sy Sz 由静力平衡force equilibrium SxdA-σxdAx-τyxdAy-τzxdAz=0 而dAx=ldA dAy=mdA dAz=ndA 所以 Sx=σxl+τyxm+τzxn 同理 Sy=τxyl+σym+τzyn Sz=τxzl+τyzm+σzn 因此S2=Sx2+Sy2+Sz2 σ= Sxl+Sym+Szn =σxl2+σym2+σxn2+2(τxylm+τyzmn+τxzln) τ2= S2-σ2
由于静力平衡 即有： 解得：
13．1．2 应力分析单元体法
变形体多向受力，用截面法不全面，需改进——单元体法！
设物体内任一单元体受力，将全应力均加以分解后，得 九个应力分量stress components，可写为矩阵：
作用面 作用
方向 注意：应力是张量tensor（标量，矢量，张量） 张量的定义：满足坐标系转换关系的分量集合 正负号：正面正向、负面负向取正号，正面负向、负面正向取负 号。 单元体平衡有：τxy=τyx τxz=τzx τyz=τzy
此式即 展开整理为：σ3-J1σ2-J2σ-J3=0 ***** 其中：J1=σx+σy+σz 可以求出三个实根σ1 σ2 σ3
分别代入前式可求出三个主方向： l1 m1 n1 l2 m2 n2 l3 m3 n3
注意：应力状态确定——主应力唯一， 即方程*****唯一,也即J1 J2 J3为不变值，分别为应力张量的第一不变量J1 第二不变量J2 第三不变量J3 应力不变量stress invariants