当前位置：文档之家 › 三向应力状态图解法的研究_王军

三向应力状态图解法的研究_王军

  • 格式：pdf
  • 大小：999.24 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

三向应力状态

三向应力状态

4.应力状态的分类：
(1).单向应力状态：三个主应力中，只有一个不为零——简单 应力状态。 (2).双向应力状态：三个主应力中，只有一个为零。 (3).三向应力状态：三个主应力都不为零 ——复杂应力状 态。 Z sz Z s2
tzy
tzx txy
sx
txz tyz dz sy Y O
dz
sy
tyx tyz sx O
5.讨论： 由右图可见：在三向应力状态下，最大，最小正应力分别 为最大，最小主应力，即：
s max = s 1
最大剪应力为：
s min = s 3
t max =
s1 s 3
2
DCA = 900 故t max 位于与 s 1 s 3 均成 450的斜面上。 又由于，
注：上述结论，同样适用于单向和双向应力状态。
s max = s A = OC CA =
s x s y
2

s x s y 2
2
2 t x
（10-3）
s min = s B = OC CB =
s x s y
2
s x s y 2
2 （10-4） t x
2
最大，最小正应力所在截面的方位角 0
三.验证 s ,t 的正确性
由应力圆可得：
y tyx sx sy n
t s
t
G1t' s,tG D(sx, txy) 2
txy
sx x
txy
B O s3
H
2
C
L
F A s1
s
sy
tyx
E (sy, tyx)
G2 t"

六、 材料力学应力状态分析(2)

六、 材料力学应力状态分析(2)

(MPa)
τ σ
（0，-100）
tmax
（300，100）
τmax = 180MPa；
Hale Waihona Puke σOσσ三向应力状态 特例分析
作为三向应力状态的特例,平面应力状态特点：
σ =0 σ、σ 、σ σ1 、σ 2、σ3
广义胡克定律
1、胡克定律、横向变形与泊松比
y
sx x = ; E sx y = x = ； E — 泊松比
tmax
（-300，50）
300
(MPa)
τ
σ
σ
（-200，-50）
σ
O
σ
三向应力状态 特例分析
例3、如图平面应力状态，求： 主应力s1、s2 、 s3和最大切 应力tmax。
300 100
解：如图作应力圆 Ｒ＝180MPa； s1 = 330MPa； s2 = 0； s3 = -30MPa；
A
2、平衡方法是分析一点处应 力状态最重要、最基本的方法
A
论证A－A截面上 必然存在切应力，而 且是非均匀分布的； 怎样证明A－A截 面上各点的应力状态 不会完全相同。
结论与讨论
A
ζ
ζ η
A
关于A点的应力状态有多种答 案、请用平衡的概念分析哪 一种是正确的。
η
η
ζ
结论与讨论
3、怎样将应力圆作为一 种分析问题的重要 手段，求解较为复杂的 应力状态问题
P
x =
由变形方程： x =
1 [s x (s y s z )] = 0； E s x = s z = 0.3( 60) = 18 MPa
P σx σy
所以铅块主应力为: ζ1 = 0；ζ2 = -18MPa; ζ3 = -60MPa;

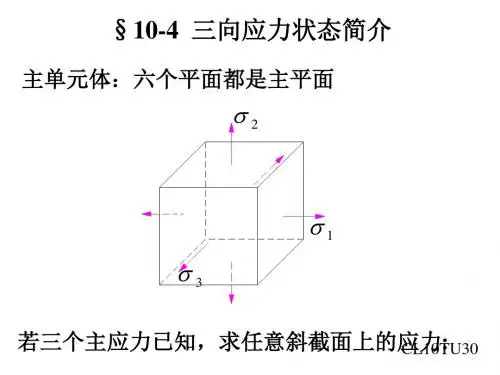
第十章-三向应力状态简介(材料力学课件)

第十章-三向应力状态简介(材料力学课件)
应力与许用拉应力之比 [ ] 0.5 [ ]
• 用第四强度理论可得出：塑性材料的许用剪
应力与许用拉应力之比 [ ] 0.577 [ ]
例：填空题。
石料在单向压缩时会沿压力作用方向的纵 截面裂开，这与第 二 强度理论的论述基本 一致。
例：填空题。
一球体在外表面受均布压力p = 1 MPa 作用，则在球心处的主应力 1 = －1 MPa， 2 = －1 MPa， 3 = －1 MPa。
1.最大拉应力理论（第一强度理论） • 它假定：无论材料内各点的应力状态如何，
只要有一点的主应力σ1 达到单向拉伸断裂时 的极限应力σu，材料即破坏。
• 在单向拉伸时，极限应力 σu =σb
• 失效条件可写为 σ1 ≥ σb
[ ] b
n
• 第一强度强度条件： 1 [ ]
试验证明，这一理论与铸铁、岩石、砼、 陶瓷、玻璃等脆性材料的拉断试验结果相符， 这些材料在轴向拉伸时的断裂破坏发生于拉应 力最大的横截面上。脆性材料的扭转破坏，也 是沿拉应力最大的斜面发生断裂，这些都与最 大拉应力理论相符，但这个理论没有考虑其它 两个主应力的影响。
V 2EA Al 2E 2
CL10TU40

变形比能：
u 1
2


u

1 2

1

1

1 2

2
2

1
2
3
3
2
1 3
变形比能：
u

1 2

1

1

1
2
2
2

1
2
3
3

应力圆的解析与图解法证明

应力圆的解析与图解法证明

应力圆的解析与图解法证明郭志昆;陈万祥;郭伟东;姜猛【摘要】应力圆以严格的应力解析表达式为理论根据.作为几何图形,应力圆是应力状态直观形象的载体,人们可以通过作图的方法方便地获得描述应力状态的有关参数,即图解法,这在计算工具尚不发达的年代很有价值.然而,图解法存在的根本依据是应力圆所具有的特性,深入系统地研究这些特性,可以深刻地揭示应力圆的本质.为此,从应力圆的理论构成入手,深入分析应力圆的理论表达式与几何图形的有机联系,并对应力圆图解法进行系统证明.【期刊名称】《力学与实践》【年(卷),期】2016(038)005【总页数】6页(P581-586)【关键词】应力圆;解析;图解法;几何特性【作者】郭志昆;陈万祥;郭伟东;姜猛【作者单位】解放军理工大学爆炸冲击防灾减灾国家重点实验室,南京210007;解放军理工大学爆炸冲击防灾减灾国家重点实验室,南京210007;解放军理工大学爆炸冲击防灾减灾国家重点实验室,南京210007;解放军理工大学爆炸冲击防灾减灾国家重点实验室,南京210007【正文语种】中文【中图分类】O341为研究一个物体不同部分之间的相互作用，通常采用“截面法”［1］.物体被想象截成两部分，截开的两个面上所有质点作用的内力，用分布在截面上的表面力代替，单位面积上的表面力称为应力.下述将采用“应力分析法”［1］对物体内部任意点的应力进行分析.过任意点的应力通常可分解成两个分量：一个与该平面的外法线平行，称为正应力（用σ表示）；一个与该平面平行，称为切应力（用τ表示）.现以σ和τ为变量建立平面直角坐标系（如图1所示），以该点的3个主应力（σ1>σ2>σ3）为参数作出如图1所示的图形.显然，图中最大的圆的圆心位于点（（σ1+ σ3）/2，0），直径为σ1-σ3，其余的两个圆的圆心分别位于点（（σ1+σ2）/2，0）和（（σ2+σ3）/2，0），直径分别为σ1-σ2和σ2-σ3.由于表示在该坐标系中的图形都是圆，而且所表示的量又是应力，因此称其为应力圆.1866年应力圆的概念首次被提出，1882年被德国人莫尔（Otto Mohr）发展和完善［2］，故又称莫尔圆.借助应力圆，莫尔给出了一种确定过一点任意斜面上的σ和τ大小的方法.其实，此后的学者还不断从不同的角度对应力圆进行研究，使其处于逐步完善之中.譬如，有学者认识到利用莫尔圆无法确定τ的方向［3］.1955年，应力圆的图解方法被提出［4-5］，但无相应证明，后来许多人也不加证明地引用了该图解方法（具体文献很多，这里无需赘引）.2000年前后，出现了一些图解法的证明［67］，但都不完整.王仲仁等［810］从多角度诠释了应力圆的构成，并给出切应力作用方向的解析式.本文基于既有成果，对应力圆进行系统论述，并对其图解法给予完整的证明.以期对有兴趣全面深刻了解应力圆的读者有所裨益.如图2所示，某点的应力状态由其3个主应力给出，其中T表示过该点的某平面上的应力，设该平面的面积为dA，其单位外法向量为式中，v1，v2，v3是v的方向余弦，又是v在坐标轴的投影（即分量）.显然则由柯西应力公式得它在v上的投影就是作用在该平面上的正应力，大小为一方面，微面积dA上内力可看作3个主方向上内力的合力，即另一方面，微面积dA上内力也是法向力与切向力的合力，即比较式（3a）与式（3b）得到就v1，v2，v3联立求解式（1）、式（2）、式（3a）～式（3c）得对式（4）～式（6）进行整理，得到不难发现，式（7）～式（9）表示的都是στ平面上的圆.由于非负，并注意σ1>σ2>σ3，式（7）～式（9）就变成式（10）～式（12）所表示的意义如图3所示，即无论v1，v2，v3在其定义域上取何值，点（σ，τ）只可能落在图3中阴影所示的闭区域中.换言之，图3表明：具有主应力σ1，σ2和σ3（σ1>σ2>σ3）的任意点，无论过该点的平面朝向何方，作用在其中的正应力及其相应的切应力的数值只可能对应着图中阴影闭区域中的某一点.显然，构成图3的3个圆是其实，的取值范围均为［0，1］，当它们分别在此范围连续取值时，式（7）～式（9）则分别表示了στ平面上圆心位于σ轴上的一个圆环.其中，在式（7）和式（9）中分别取等于0，都得到圆环的内缘，而取等于1，都得到圆环的外缘；在式（8）中分别取等于0和1，则得到圆环的外缘和内缘.这3个圆环的圆心和内外直径详见表1.将它们迭画在同一张图（图4）中，其公共区域就是图3的阴影部分. 必须强调，当σ1，σ2和σ3中仅有一个为0时，即所考察的点处于平面应力状态，应力圆的基本构成仍然是图4所示的情况，不同的是图形在坐标横轴（σ轴）上平移，使得坐标系原点O与0主应力重合.尤其值得注意的是，对于σ1和σ3中的一个为0时的平面应力状态，最大切应力仍然成立.遗憾的是，在论及这两种平面应力状态时，总有人将最大切应力写成τmax=（σ1-σ2）/2或τmax=（σ2-σ3）/2.众所周知，借助平面应力圆，可以很方便地通过作图得到垂直于所讨论平面的任意斜面上的应力分量，或根据已知应力分量找到其所在的斜面，这就是平面应力圆的图解法.尽管精度可能不尽如意，图解法在计算工具不发达的年代实用价值巨大.现代计算手段让图解法走下神坛，但是，它形象直观的“解读”功能犹在，并不可替代.这里列举应力圆的一种图解法［5］.方便起见，将构成应力圆的3个圆分别命名为C1，C2和C3，以O1，O2和O3分别表示它们的圆心，以T1，T2，T3分别表示C2和C3，C3和C1，C1和C2的切点（图5）.设拟考察的面已知，即v1，v2，v3明确.不妨令首先，分别过T1和T3引垂直于σ轴的垂线（根据其作用，不妨称其为方向角基准线）L1和L3；接下来，作过T1与L1成α角的直线分别交C2和C3于点A和B，作过T3与L3成γ角的直线分别交C1和C2于点E和F；第三步，过点A和B作C1的同心圆弧，过点E和F作C3的同心圆弧，俩圆弧的交点P的坐标值就是所考察面上的正应力和切应力.注意，作图的第三步隐含着这样一个要求：圆心既定，由第二步确定的两个点（A 和B，或E和F）必须共圆.这个要求存在吗？进一步，所找到的点P的确如此吗？对这两个问题证明如下：对第一个问题，为清晰起见，从图5中剔除无关内容得图6.如证得O3E=O3F，即得证.为此，过O3作O3G⊥EF，故T2E//O3G//T1F；而O3T1=O3T2，故EG=GF，即O3G是△EO3F的底边EF的垂直平分线，故△EO3F是等腰三角形.于是点E和F必定共处以O3为圆心的一个圆上；作图时，以O3为圆心过点E和F 中一个画圆，圆弧必定经过另一个点.同理可知点A和B必定共处以O1为圆心的一个圆上.对第二个问题，以r1，r2和r3分别表示圆C1，C2和C3的半径.已知O3P=O3E=O3F，O1P= O1A=O1B.在△T3EO3中，T3E=2r1sinγ，T3O3=2r1+r3，cos∠ET3O3=sinγ由余弦定理可知在△T1PO1中，T1O1=r1+2r3，T1P= 2r2sinα，cos∠PT1O1=sinα由余弦定理可知在△O1PO3中，O1O3=r2，由余弦定理可知由于O1A和O3E分别是C1和C3的同心圆的半径，故可以用式（7）和式（9）分别校核式（14）和式（13）的正确性.在△OPO3中，，由余弦定理可知将式（13）～式（15）代入式（16）中，并结合式（1）和式（3），整理得过点P作垂线交σ轴于点P0，OP0就是OP在σ轴的投影对照式（2），正是T的正应力分量σ，此时，其切应力分量τ就很容易求出.过切点T2作直线可同时与三个圆相交，除点T2外，还有4个交点（如图5），此时的情况又如何呢？其实不难证明，只有位于“相关圆”（当前切点所联系的俩圆）上的俩交点才共驻第三个圆的某个同心圆.进一步，改变作图次序，先过点P作C2的同心圆交C1和C3于点C，D，C0和D0（如图7所示，显然，C和C0，D和D0分别关于σ对称），再过点C和D或C0和D0作直线，该直线是否一定经过点T2？如果是，v2=cosφ（φ为CD与方向角基准线L3的夹角）成立吗？对于第一个问题，设直线CD、直线C0D0与直线T1T3交于A点，圆C1、圆C2、圆C3的半径分别为r1，r2，r3，先明确一个几何关系，O1O2=r3，O2O3=r1，△O1CO2～=△O3O2D，故∠CO2O1=∠O2DO3，由等腰△O2CD及对顶角相等的几何关系可以证明∠O3AD=∠O3DA，故CD与T1T2的交点A与切点T2重合，即直线CD，直线C0D0过切点T2.对于第二个问题，在△T2DO2中，T2O2=r2-2r1，T2D= 2r3sinφ，cos∠DT2O2=sinφ.由余弦定理可知而O2D又是过点P以O2为圆心的圆的半径，以O2为圆心的圆的方程是式（8）.比较式（8）与式（17）的右边，并考虑点P是圆C1，C2和C3的同心圆的公共交点，故即必定成立.切应力分量τ的方向不如正应力的方向那样显而易见，可由下列方法确定.前面已经给出单位外法向量为v=v1i+v2j+ v3k的平面上的应力而相应正应力的向量形式为用表示相应切应力τ的方向余弦，则由于故（1）应力圆一般由3个两两相切、圆心共线的圆构成；对于两向主应力相等（包括等于0）状态，应力圆是单个圆；对于三向主应力相等（包括等于0）状态，应力圆是一个点，切应力为0.（2）图3的阴影闭区域由三簇同心圆的公共交点组成，即该区域中的任意点都同时有3个不同的圆经过，所以这些圆的圆心位于切应力（τ）为0的直线上. （3）过切点T1，T2或T3的直线与相关圆均有3个交点，除本切点外的两个交点必定同在第3个圆的同心圆上.（4）若过切点T1，T2和T3的直线与各自的方向角基准线L1，L2和L3的夹角分别用α，β和γ表示，且cos2α+cos2β+cos2γ=1成立.则按结论3所作出的3个圆必定相交于同一点.该点的坐标值（σ，τ）是单位法向为v=±（cosα）i±（cosβ）j±（cosγ）k的平面上的正应力和切应力.（5）应力圆中无法直观描述有关向量的方向，但相应地解析式弥补了这一缺陷.【相关文献】1 陈惠发，萨里普AF.土木工程材料的本构方程.余天庆，王勋文译.武汉：华中科技大学出版社，20012 Mohr O.Uber die Darstellung des Spannungszustandes uddes Deformationszustandes eines Korpere lemenltesund uber die Anwendung derselben in der Festilakeitslehve. Zivilingenieur，1882，28:112-1553 Swift HW.Plastic strain in an isotropic strain hardening material.Engineering，1946，163:381-3894 Derrington MG，J ohnson W.The shortcoming of Mohr’s circle for three-dimensional stress.Bulletinof Mechanics Engineering Education，l960，16:247-2555 Johnson W，Mellor PB.塑性理论.王则明译.上海：上海科技出版社，19556 韩秀清，杨光，李凌飞.关于一点应力状态作图法的一种综合证明.吉林工业大学自然科学学报，2001，31（3）:45-487 王军，马庆捷.三向应力状态图解法的研究.吉林化工学院学报，2005，22（3）:71-738 王仲仁.塑性加工力学基础.北京：国防工业出版社，19899 王仲仁，何祝斌.三向应力Mohr圆的真实构成及剪应力作用方向的确定.力学季刊，2003，24（3）:401-40610 王仲仁，苑世剑，胡连喜等.弹性与塑性力学基础.哈尔滨：哈尔滨工业大学出版社，2007。

三向应力状态图解法的研究_王军

三向应力状态图解法的研究_王军

吉 林化工 学院 学报 JO UR NAL O F JILIN INSTITU TE O F CHEM ICAL TECHN OLO GY
文章编号: 1007- 2853( 2005) 03- 0071- 03
三向应力状态图解法的研究
V ol. 22 No. 3 Jun. 2005
王 军, 马庆捷
( 吉林化工学院 机电工程系, 吉林 吉林 132022)
5结 论
三向应力状态下, 任意斜截面上的应力分量理 论证明这一点 D 落在三向应力圆的阴影部分, 通 过图解法可以很容易的找出应力分量所在的这一 点 D, 任意斜面上的应力分量可直接量取, D 点的 横坐标是 0, D 点的坐标是 0, OD 的长度是 P0, 使工程力学应力分析的方法都可以应用图解法来 分析.
摘要: 证明了三向应力状态斜截面上应力分量与三向应力圆阴影部分 相对应, 研究了 用图解法画出三向
应力状态斜截面上应力分量的方法.
关 键 词: 三向应力状态; 应力圆; 斜截面; 应力分量; 图解法
中图分类号: T B 301
文献标识码: A
应力状态包括单向应力状态, 二向和三向应力 状态, 对于单向和二向应力状态的应力分析解析法 和图解法在工程力学中都有较详细的论述. 但三向 应力状态的应力分析只有解析法定性的论述, 没有 图解法的分析. 而解析法又非常繁杂. 本文研究了 用图解法画出三向应力状态斜截面上应力分量的 方法, 使工程力学应力分析的方法都可以应用图解 法来分析, 使讲授工程力学的教师和工程技术人员 解决实际问题有了既简便又准确的方法.
Key words: three dimensional stress state; stress circle; skew section; stress component ; graphic met hod

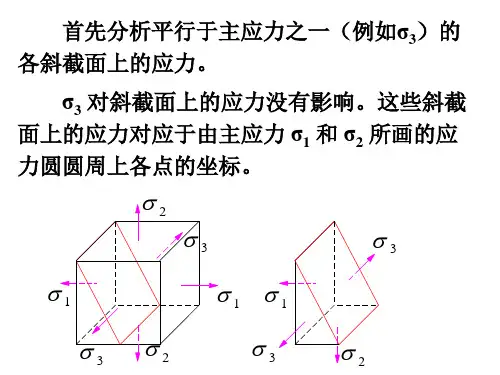
三向应力状态简介

三向应力状态简介


变形比能： 1 u 2

2

1 1 1 u 1 1 2 2 3 3 2 2 2
1 3
变形比能： 1 1 1 u 1 1 2 2 3 3 2 2 2
1 2 2 1 2 2 3 2 ( 1 2 2 3 3 1 ) 2E 1
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
解： 1 50MPa
2 50MPa 3 50MPa max 1 3
2 50MPa
CL10TU33
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
CL10TU34
解：
120 40 2 2


3(1 2 ) 2 1 2 2 m ( 1 2 3 ) uv 2E 6E
u f u uv
12 2 2 2 m ( 1 2 ) ( 2 3 ) ( 3 1 ) 6E
m
1 2 3
3
3 ( 1 2 ) 1 2 3 m 变形比能 = 体积改变比能 + 形状改变比能 E 3 K u = u + u
v
f CL10TU41
1 2 2 u 1 2 2 3 2 ( 1 2 2 3 3 1 ) 2E
1 式中：
E 1 体积弹性模量 K 3 (12 2 ) 2 （ 3 1 ） E 1 2 3 m 1 3 3 （ 1 2 ） 3 E 当 05 . 时， 0
2
3 1
1 3

三向应力状态下的应力——应变曲线及其应用

三向应力状态下的应力——应变曲线及其应用
何宇廷;傅祥炯
【期刊名称】《西北工业大学学报》
【年(卷),期】1998(016)004
【摘要】应用弹塑性力学的基本原理，推导了由材料单调拉伸应力－应变（σ－ε）曲线求得三向应力状态下应力－应变（σ１－ε１）曲线的表达式。

实验结果验证
了理论分析结果的正确性，并用σ１－ε１曲线解释了材料在受三向拉应力时机械
性能的变化以及带裂纹构件在裂纹扩展时裂纹前缘形状变化的原因。

【总页数】6页(P610-615)
【作者】何宇廷;傅祥炯
【作者单位】西北工业大学;西北工业大学
【正文语种】中文
【中图分类】O344.1
【相关文献】
1.多轴应力状态下的局部应力应变近似计算方法及其应用 [J], 王相平;王桂华
2.应用内应变测量技术测定混凝土应力—应变曲线的研究 [J], 陈绍炳;蒋家奋
3.三向应力状态下的岩石强度曲线 [J], 杨长清;张家生
4.MnS高温应力-应变曲线及其在有限元分析中的应用 [J], 金淼;于琳琳;刘鑫刚;郭宝峰
5.MnS高温应力-应变曲线及其在有限元分析中的应用 [J], 金淼; 于琳琳; 刘鑫刚; 郭宝峰
因版权原因，仅展示原文概要，查看原文内容请购买。

三向应力状态PPT精选文档


x
max1 x min3 -x
此现象称为纯剪切
22
7-3 空间应力状态
1、空间应力状态的概念
三个主应力均不为零
23
2、最大正应力和最大剪应力
max 1
max
1 -3
2
24
3、广义虎克定律
单向应力状态下有
纵向应变
E
横向应变 - -
E
由1引
起
的
应变 1
1
E
由2引起
的
应
变 1
外法线方向为正，反之为负。 正应力：拉为正，压为负。 剪应力：使微元体或其局部产生顺时针方
向转动趋势者为正，反之为负。12
N0 a dA+( xy dAcosa)sina-(x dAcosa)cosa +( yx dAsina)cosa-(y dAsina)sina0
T=0 a dA-(xy dAcosa)cosa-(x dAcosa)sina +(yx dAsina)sina+(y dAsina)cosa0
其强度条件为：
A
n
对于复杂应力状态，危险点的应力并不取决于横截 面上的应力，也不仅仅取决于最大应力，而需要考 虑各个方向的应力的共同作用
长期生产实践中，人们提出某些假说，称为强度理论， 常用的有4种
29
2、常用的强度理论的概念
（1）最大拉应力理论（第一强度理论）
最大拉应力是引起材料断裂破坏的主要因素， 破坏原因： 即认为无论是单向或复杂应力状态，第一主应
max min
x
+ 2
y
x
2
y
2
+
2 x
10 + 30 10 - 30 2 + 20 2

三向应力状态的广义胡克定律叠加法课件3

2
这个方程恰好表示一个圆，这个圆称为应力圆
（圆上各点即为对应的正应力和切应力大小）
1.应力圆：
(
x
y
)2
2
2
(
x
y
)2
2 xy
2
R
(
x
y
)2
2 xy
R
2
C
x y
2
2.应力圆的画法
y y yx
D xy
A x
x D/
(y ,yx)
R
(
x
y
)2
2 xy
2
R
D (x ,xy)
c
x y
2
3、几种对应
都是由于微元内的最大拉应力达到简单拉伸时的破 坏拉应力数值。
1 0 1 －构件危险点的最大拉应力 0－极限拉应力，由单拉实验测得 0 b
最大拉应力理论（第一强度理论）
断裂条件 强度条件
1 b
1
b
n
铸铁拉伸
铸铁扭转
2. 最大伸长拉应变理论（第二强度理论）
无论材料处于什么应力状态,只要发生脆性断裂,
i
n
2
α0 τx
yc
o
s
2
α0
2τα0
0
即α＝α0 时，切应力为零
tan 2 0
2 xy x
y
tan 20
tan（2
/ 2 - 0）
2 xy x
y
设（ / 2 0 ) 0 则0 0 / 2
由上式可以确定出两个相互垂直的平面（，分
别为最大正应力和最小正应力（主应力）所在平面。
2
3、广义胡克定律的一般形式
z

复杂应力状态分析2应力圆法


O
px A
OBC的面积为mdA
pz C
（A） OCA的面积为ndA
3
OAB的面积为ldA
z
2 1
x
y B
py
1 O
pz C
（B）平衡方程
X 0 px dA 1 mdA 0
2
Y 0 p y dA 3 ndA 0
px
Ax
Z 0 pz dA 2 ndA 0
（C）
p2
则E 点坐标： E（52.3，-18.7）
50
σ2
20 σ1
D′（50，20）
30 x A
C
σ1
σ2 0
20
B
3、主应力及主单元体
D（30，-20）
C（40，0） r 22.4 o 31.7o B点： 1 40 22.4 62.4(MPa)
A点： 2 40 22.4 17.6(MPa) 3 0
( n
2
3 )2
2
2 n
(
2
3
)2
2
(
n
3
2
1
)2
2 n
(
3
2
1
)2
(
n
1
2
2
)2
2 n
(
1
2
2
)2
结论：
σ3 σ2
σ1
任意斜截面上的应力，都落在图示阴影部分内，既阴影部 分内每一个点与一个截面上的应力相对应。
三、一点处应力状态中的 最大剪应力
max
1
3
2
★与二向应力状态中最大剪应力的区别：
与x轴的夹角为a，则
推论：
1
2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

l = m= n= 1; 3
= = = 54. 7 以 0 表示该斜截面上的正应力, 0 表示剪应 力, 则合力为
p0=
2 0
+
2 0
=
p
2 x
+
p
2 y
+
p
2 z
= 59. 511 9 MPa
0 = lp x + mpy + mp z
= 25 MPa
0=
1) 2]
1 2
1 3
[
(
1-
2) 2 + ( 2 -
( a)
( b) 图 2 图解法求 n、n 示意图
( 4) 由圆 K 23 与 K 12 的圆心 O1、O 3 画弧 ED 与 FD, 此二弧相交于 D 点. D 点的坐标即表示法线为 n 的平面上的正应力和剪应力, 而 OD 的长度表示 该面上的总应力 Pn.
3 图解法正确性的证明
首先计算半径第度 O 1E = r 1, O3 F = r 2, 由 O 1A E, r 12 = O 1A 2 + AE 2 - 2O 1 A A Esin
Key words: three dimensional stress state; stress circle; skew section; stress component ; graphic met hod
n-
1+ 2
2
2+
2 n
=
12
2
2 + n2( 3-
1) ( 3 - 2)
( 1)
( 1) 式中的 l 、m 、n 为斜截面的三个方向角余
弦. 当 1、2、3 和 l 、m、n 已知后, 可以作出( 1) 式
图 1 三向应力示意图
BC 的 圆 为:
2-
2 3
2
n-
2+ 2
3
2
+
2 n
=
说明( 1) 式中的第一式所确定的应力圆周在
任意斜截面上的应力 n、n 如图 1( b) 所示, 可以通 过理论计算得知[ 1] . 在以 n 为横坐标, n 为纵坐标 的坐标系中, 由下列三个圆周的交点的坐标值来表
达.
n-
2+ 2
2
3+
2 n
=
22
3
2
+ l2(
1-
2) ( 1 - 3)
n-
3+ 2
2
1+
2 n
=
32
2
1 + m2( 2
- 3) ( 2 - 1)
( 2) 由于:
O1 A = 入( 2) 有:
r
2 1
=
1-
2+ 2
3 及AE = ( 1-
3)sin 代
1-
1 2
(
1+
2
3) + [ ( 1-
3) sin ] 2
-2
1-
1 2
(
2+
3) ( 1 -
整理后,
得:
r
2 1
=
(
1-
1 4
(
2-
3) 2
类似可得:
r
2 2
=
(
1-
3) sin2 3) ( 1 -
文献标识码: A
应力状态包括单向应力状态, 二向和三向应力 状态, 对于单向和二向应力状态的应力分析解析法 和图解法在工程力学中都有较详细的论述. 但三向 应力状态的应力分析只有解析法定性的论述, 没有 图解法的分析. 而解析法又非常繁杂. 本文研究了 用图解法画出三向应力状态斜截面上应力分量的 方法, 使工程力学应力分析的方法都可以应用图解 法来分析, 使讲授工程力学的教师和工程技术人员 解决实际问题有了既简便又准确的方法.
4举 例
图 3( a) 中取 1、2、3 的方向为坐标轴 X 、Y 、 Z 的方向, 1 = 75 MPa, 2 = 50MPa, 3 = 50 MPa, 剪应力分量全为零, 试求与三个应力主轴成等角倾 斜面上的应力分量.
理论计算如下:
第 2期
王 军, 等: 三向应力状态图解法的研究
73
该斜截面法线的方向余弦为
3)( 2 -
2) cos2 + ( 3)
3) cos2 +
1 4
(
1-
2) 2
( 4)
如令 D O1 O 3 = , 则由 DO 1 O 3 可得:
D O23 =
O1 D 2 +
O1
O
2 3
-
2O1 D
O 1 O 3cos
( 5)
由
DOO 1 得: OD 2 =
DO
2 1
+
OO
2 1
+
2D O1 OO 1cos
n、n 可以通过公式( 1) 中的三个圆的交点求出, 但
是在求解的过程中, 计算繁杂, 而应用图解法来找 到 D 点坐标却相对简单, 如图 2, 其作法如下.
1) 在 、 直解坐标中, 在 轴由原点取线段 OA = 1, OC = 2。OB = 3 图 2( b) .
2) 以 AB、BC、CA 为直径画出莫尔圆. 3) 由 A 点作与 轴成 角( 按逆时针方向) , 并引直线与圆 K 13 交于点 Eo 由 B 点作与 轴成 角( 按顺时针方向) , 并引直线与圆 K 13 交于 F 点.
3) 2 + ( 3 +
= 54 MPa 图解法如下:
作出三向应力圆如图 3( b) 所示, 作 A E 与竖直 夹角 54. 7 交 AB 于 E 点, 作 BF 与竖 直夹角
54. 7 交 A B 于 F 点, 以 BC 的圆心 O1 为圆心, O 1E 为半径作圆弧 ED , 以 A C 的圆心 O 3 为圆心,
( 6)
式中 D O1 = r 1, DO 3 = r 2 为简化计算, 引入
O1O3 =
1 2
(
1-
3) = a
( 7)
OO 1 =
1 2
(
2+
3) = b
将( 7) 代入( 5)( 6) 并消去 cos , 得
OD 2 =
1 a
[
r
2 1
+
ab) ( a +
b) - br22] 即
OD 2 =
21cos2 +
参考文献:
[ 1] 刘鸿文. 材料力学[ M] . 北京: 高等教育出版社, 1993.
[ 2] 徐 秉业. 弹 性与塑 性力 学[ M] . 北京: 机械 工业出 版
( a)
社, 1988.
Study on graphic method to three dimensional stress states
图 1( a) 中的阴影线的部分之内
2 图解法求任意斜截面上的应力
虽然对于三向应力状态任意斜截面上的应力
收稿日期: 2005- 03- 18 作者简介: 王 军( 1961- ) 男, 河北保定人, 吉林化工学院副教授, 主要从事机械力学及实验应力分析方面的研究.
72
吉 林化 工学 院学 报
2005 年
b+
r
2 1
+
a2 -
r
2 2
2a
用应力表达并引入 l2 + m 2 + n2 = 1 有:
OD 1 = l 2 1 + m2 2 + n2 3 = n
( 10)
D 点的纵坐标为:
DD 1 =
OD 2 -
OD
2 1
=
pn2 -
2 n
=
n
( 11)
式( 10) 和( 11) 表明, D 点的坐标表示斜截面 上的正应力和剪应力[ 2] .
2 2
(
1
-
cos2
- cos2 ) +
2 3
cos2
( 8)
把方向余弦的关系式 l 2 + m2 + n2 = 1 代入
( 8) 有: OD 2 =
l2
2 1
+
m2
2 2
+
n2
2 3
=
p
2 n
( 9)
式( 9) 表示线段 OD 的长度, 表示斜面上的总
应力[ 2] . D 点的横坐标为:
OD 1 =
5结 论
三向应力状态下, 任意斜截面上的应力分量理 论证明这一点 D 落在三向应力圆的阴影部分, 通 过图解法可以很容易的找出应力分量所在的这一 点 D, 任意斜面上的应力分量可直接量取, D 点的 横坐标是 0, D 点的坐标是 0, OD 的长度是 P0, 使工程力学应力分析的方法都可以应用图解法来 分析.
第 22 卷 第 3 期 2005 年 6 月
吉 林化工 学院 学报 JO UR NAL O F JILIN INSTITU TE O F CHEM ICAL TECHN OLO GY
文章编号: 1007- 2853( 2005) 03- 0071- 03
三向应力状态图解法的研究
V ol. 22 No. 3 Jun. 2005
WANG Jun, MA Qing- jie
( Department of M achinery and Electricity Engineer ing, Jilin Institute of Chemical Technology , Jilin City 132022, China)
Abstract: It is proved that stress component of skew sect ion about three dimensional stress state is corresponding to shaded parts of three dimensional stress circle, and the met hod of draw ing stress component of three dimensional stress state skew sect ion wit h graphic method is researched.