当前位置：文档之家 › 二向应力状态分析--解析法和图解法.

二向应力状态分析--解析法和图解法.

  • 格式：ppt
  • 大小：2.20 MB
  • 文档页数：52

下载文档原格式

  / 52

合集下载

应力状态概述二向和三向应力状态的实例二向

应力状态概述二向和三向应力状态的实例二向

2．作应力圆 主应力为 1 , 3 ，并可 确定主平面的法线。
材料力学
第七章
应力和应变分析
3．分析 纯剪切应力状态的两个主应力绝对值相等， 但一为拉应力，另一为压应力。由于铸铁抗拉强度较 低，圆截面铸铁构件扭转时构件将沿倾角为 45º 的螺旋面因拉伸而发生断裂破坏。
材料力学
第七章
2 2
x y
xy

n

材料力学
y a xy
y On D( x , ) a a
a
第七章
n
应力和应变分析
二、应力圆的画法
建立应力坐标系，如下图所 示，（注意选好比例尺） 在坐标系内画出点A( x， xy)和B(y，yx)

x
C O
2a
AB与a 轴的交点C便是圆 A( x , xy) 心。
150°
第七章
应力和应变分析
x y 2 2 1 x y （ ） xy 2 2 2
解法2—解析法：分析——建立坐标系如图
95
60°
y 45MP a yx 25 3MP a xy
25 3
x ?
y O x
60 95MPa 60 25 3MPa
材料力学
第七章
应力和应变分析
应力表示——单元体：
①dx、dy、dz（微小的正六面体） ②单元体某斜截面上的应力就代表了构件内 对应点同方位截面上的应力。
B P
dz
dx
dy
A
C
பைடு நூலகம்
B
D
C
B、C——单向受力，τ ＝0 A——纯剪切， σ ＝0
D
D——既有 σ ，又有τ

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

应力圆概念

应力圆概念

σ1
例题7-1 从水坝体内某点处取出的单元体如图所示, sx= - 1MPa , sy= - 0.4MPa , tx= - 0.2MPa , ty= 0.2MPa , （1）绘出相应的应力圆 （2）确定此单元体在 a =30°和a = - 40°两斜面上的应力。
σy τy
σ x = -1
σx τx
C
D1 (-1,-0.2)
B2
s
(2) 确定 a = 30°斜截面上的应力 将 半径 CD1 逆时针转动 2a = 60°到半径 CE, E 点的坐标就
代表 a = 30°斜截面上的应力。
(-0.4,0.2) t D2 B1 C o
B2
D1 (-1,0.2)
s
σ 30 = -0.68 MPa
0
60
C
D1 (-1,0.2)
B2
σ -40 = -0.95 MPa
0
τ -40 = 0.26 MPa
0
σ 30 = -0.68 MPa
0
τ 30 = -0.36 MPa
0
σ -40 = -0.95 MPa
0
τ -40 = 0.26 MPa
0
y
α =30
0
x
α = 400
例题 7-2 两端简支的焊接工字钢梁及其荷载如图 a , b 所示,
0
τ 30
E
τ 30 = -0.36 MPa
0
0
σ 30
0
(3) 确定 a = - 40°斜截面上的应力 将 半径 CD1 顺时针转 2a = 80°到半径 CF, F 点的坐标就 代表a = - 40°斜截面上的应力。 F
σ -40
-80

应力状态的概念

应力状态的概念

t xy 10MPa
600
600
n
s
40 (20) 2
40 (20) cos(1200 ) (10) sin(1200 ) 2
13.67MPa
t
40 (20) sin(1200 ) (10) cos(1200 ) 21MPa 2
20MPa
10MPa
300
40MPa
300
xn
解： s x 20MPa
P
A
P sx
sx
A
y
B
C z
P
sx B sx
Mx
tzx
txz
课堂练习
t yx
t C
xy
用单元体表达圆轴受扭时，轴表面任一点旳应力状态。
用单元体表达矩形截面梁横力弯曲时，梁顶、梁底及其他各
点旳应力状态。
七、主平面、主应力：
sy
y
主平面(Principal Plane)： 剪应力为零旳截面。
sx
sz
z
1 2 3
体积应变与应力分量间旳关系:
1 2
E
(s 1
s2
s3)
例5 已知一受力构件自由表面上某一点处于表面内旳主应变分别
为：1=24010-6， 3=–16010-6，弹性模量E=210GPa，泊松比 为 =0.3， 试求该点处旳主应力及另一主应变。
1 E
s
z
s
x s
y
xy
t
xy
G
yz
t
yz
G
zx
t zx
G
上式称为广义胡克定律
主应力 --- 主应变关系
s1 s3
1
1 E

硕士建筑与土木工程专业初试专业课目(材料力学)考试大纲 (1

硕士建筑与土木工程专业初试专业课目(材料力学)考试大纲 (1

西京学院2015年
一、基本内容
1. 绪论
材料力学的任务,变形固体的基本假设,外力及其分类,内力、截面法和应力的概念, 变形与应变,杆件变形的基本形式。

2. 拉伸、压缩与剪切
直杆轴向拉伸或压缩时横截面上的内力和应力,直杆轴向拉伸或压缩时斜截面上的应力,材料拉伸时的力学性能,材料压缩时的力学性能,失效、安全因数和强度计算,杆件轴向拉伸或压缩时的变形,拉伸、压缩的超静定问题,温度应力和装配应力,应力集中的概念,剪切和挤压的实用计算。

3. 扭转
外力偶矩，扭矩和扭矩图,纯剪切,圆轴扭转时的应力、变形，薄壁杆件的自由扭转。

4．弯曲内力
弯曲的概念，受弯杆件的简化，剪力和弯矩，剪力方程和弯矩方程，剪力图和弯矩图，载荷集度、剪力和弯矩之间的关系，平面曲杆的弯曲内力。

5．弯曲应力
纯弯曲，弯曲正应力，弯曲切应力，强度条件，提高弯曲强度的措施。

6．弯曲变形
挠曲线的微分方程，积分法求弯曲变形，叠加法求弯曲变形，简单超静定梁，减小弯曲变形的一些措施。

7．应力和应变分析、强度理论
应力状态概述，二向应力状态分析——解析法，二向应力状态分析——图解法，三向应力状态。

位移与应变分量，平面应变状态分析，广义胡克定律，复杂应力状态下的应变能密度，四种常用强度理论，莫尔强度理论，构件含裂纹时的断裂准则。

8．组合变形
组合变形和叠加原理，拉伸或压缩与弯曲的组合，偏心压缩和截面核心，扭转与弯曲的组合，组合变形的普遍情况。

9．压杆稳定
压杆稳定的概念，两端铰支细长压杆的临界压力，其他支座条件下细长压杆的临界压力，欧拉公式的适用范围，经验公式，压杆的稳定校核，提高压杆稳定性的措施
10.动载荷、交变应力。

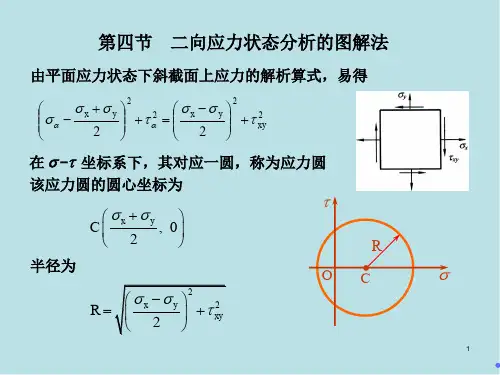
材料力学08应力状态分析_2图解法

材料力学08应力状态分析_2图解法


x

2
y
2

2 xy
OC

1
一、应力圆的画法
1. 在 - 坐标系中确定两点： D (x , xy )、D′(y , yx )
2. 连接 D、D′，交 轴于
C点 3. 以 C 点为圆心、CD 为半
径作圆即得
2

二、由图解法（应力圆）确定斜截面上的应力
将 CD 沿同样的转向旋转 2 至 CE ，则 E 点的横坐标、纵坐标即 为 斜截面上的正应力、切应力，即有
在主平面。
11
[例3] 在过 A 点的两个截面上的应力如图所示，试用图解法确定其 主应力以及主平面位置。

D
20 MPa 60 MPa
20 MPa
C B1 O
D
20 20

A1
60
解： 1）画应力圆
按选定比例尺，由 y = 20 MPa、yx = -60 MPa 确定 D′点，由 = -20 MPa、 = 0 确定 B1 点。由于B1、 D′均在应力圆的圆周上，故 作 B1D′的垂直平分线，交 轴于点 C ；以点 C 为圆心、CD′为半径
故在单元体上，从 x 轴以顺时针转向量取 0 = 33.5°，即得 1
所在主平面。
主应力单元体如图所示
14
作出应力圆。
12

D
20 MPa 60 MPa
20 MPa
C B1 O
2）确定主应力和主平面
D
20 20 70 110
根据应力圆，按选定比例尺，量得主应力
60
A1

20 MPa
1 OA1 110 MPa 2 0 3 OB1 20 MPa

二向应力

二向应力
2
(a)当 (a)当σx>σy时,
− 2τ xy 2α0 = arctg σ −σ y x
此时, 2α = 2α0 +180° 得到 σmin (主应力） 主应力）
σmin
σx +σ y = − 2
σx −σ y 2
2 +τ xy
f
t
t
由
∑n = 0
即
可得
σα dA − (σxdAcosα)cosα + (τ xdAcosα)sin α −
(σ ydAsin α)sin α + (τ ydAsin α) cosα = 0
σα = σ x cos2 α +σ y sin 2 α − 2τ x sin α cosα
1 cos2 α = (1+ cos 2α) 2 1 2 sin α = (1− cos 2α) 2
α1 = ±45°
具体是正负可由力的合成定理直接判断. 具体是正负可由力的合成定理直接判断.
（1）最小主应力及作用平面 由
σx +σy σx −σy σα = cos 2α −τ xy sin2α + 2 2
作三角变换得
σx +σ y σα = + 2
当
σx −σ y 2
二、主应力和主平面 主平面: 主平面 一点处剪应力等于零的平面称为主平面 主应力: 主应力 主平面上的正应力称为主应力 说明: 一点处必定存在这样的一个单元体, 说明 一点处必定存在这样的一个单元体 三个相互垂直 的面均为主平面, 三个互相垂直的主应力分别记为 σ1 ,σ2 , σ3 的面均为主平面 且规定按代数值大小的顺序来排列 即 且规定按代数值大小的顺序来排列, 值大小的顺序来排列

理论力学14应力状态分析

理论力学14应力状态分析
2
2


2 xy
在 - 坐标系下，其对应一圆，称为应力圆。
该应力圆的圆心坐标为
半径为
C


x
2

y
,
0

R


x

2
y
2

2 xy
30
x y
2

x
y
2
cos 2
xy
sin
2
30 50 30 50 cos 60 20sin 60 52.3 MPa
2
2
30


x

2
y
sin
2

xy
cos
2
30

30 50 sin 60 20cos 60 18.66 MPa
3
3. 切应力最大值
max
五、单向应力状态
1. 斜截面上的应力



2

2
cos 2



2
sin 2



2. 主平面和主应力
主平面： 主应力：
0 0
1 1 0
2 0 2 0
3 0 3
3. 最大切应力及其所在平面
最大切应力所在平面： 最大切应力：
45°斜截面
max


2
[例1] 试求图示单元体指定斜截面上的正应力和切应力（图中应 力单位为 MPa）
解： 对于图示单元体，有 x 30 MPa y 50 MPa xy 20 MPa 30 代入相应公式，即得指定斜截面上的正应力和切应力

材料力学第9章应力分析强度理论

材料力学第9章应力分析强度理论
已知如图，设ef 面积为dA
F
n
0
F 0

dA ( xydAcos ) sin ( x dAcos ) cos ( yxdAsin ) cos ( y dAsin ) sin 0
dA ( xydAcos ) cos ( x dAcos ) sin ( yxdAsin ) sin ( y dAsin ) cos 0
2
2 xy
xy
min
y
yx
23
⒉主方向
应力圆：D点顺时针转2α0到A1点
单元体：x轴顺时针转α0到主平面法线
证明：
xy 2 xy AD tg 2 0 CA x y x y 2
24
㈣利用应力圆求剪应力极值 应力圆上最高点、最低点的纵坐标值，为剪 应力的极大、极小值。 证明：
2
?
min
tg 2 0
2 xy
max
yx
x
x y
xy
解出两各极值点α0,α0=90+α0 最大、最小应力即为主应力
max x y x y 2 2 ( ) xy min 2 2
y
σmax、σmin为三个主应力中的两个。
11
讨论： ⑴若代数值σx≥σy，则α0、α0中，绝对值较小者是
σx与σmax之间夹角，且小于45。 ⑵若代数值 σx≤σy ，则α0 、α0 中，绝对值较小者是 σx 与 σmin之间夹角，且小于45。
min
max
yx
x
xy
12
y
㈢τmax、τmin(与z轴平行的任意斜截面上的)

材料力学

材料力学

50 100 50 100 cos60 70sin 60
2
2
73.1MPa
30
x
y 2
sin 2
xy cos2
50 100 sin 60 70cos60 2
30MPa
（2）主应力及主平面的方位

max m in


0
tan 21


x 2 xy
y
上式可求出相差900的两个角a 1，对应两个互相垂直的极值切应力截 面。

m
ax

min



x

2
y
2


2 xy
比较公式 可见 所以有
tan 20



2 xy x
y
tan
21


x xy
y

max min


x
y
2


x

2
y
2

2 xy
三、最大切应力及其作用平面的位置


x
y
2
sin 2
xy cos 2
令 1 时
即
d 0 d
d d
( x
y ) cos21 2 xy sin 21
tan 2 0


1
tan 21
2a1

2a0

π 2
,
a1

a0

π 4
例 图a所示为受力构件内单元体各面上的应力，试用

二向应力状态分析

二向应力状态分析

1.04 MP（ a 压应力）
CQ IC Z CS b Z5 2 0 10 3 0 6 1 00 5 3 2 0 0 10 - 0 9 72 0 522 0 1 5 1 0 - 0 9 - 0 312
0.46 M 9Pa
已知：C -1.04MPaC 0.469MPa
4 0x+ 2y
b
M1
1、画各点应力状态图 13 x+ 2y1 2 x-y2+4x 2
z
25mm
1
2
3
2
4
h
1
3
3
F s 4 2、计算各点主应力
1点 bh 3
I z 12
500cm4
1
My Iz
11000M 103P5a0 500104
2点 (处于纯剪状态)
120 3 -100MP
m
3点
3
aMxI(一zy 23般FA1平5s 050M 面0103320状P301M 1a态06224010P5)1a1500038.6M FIszSP bz*a121322.502M M 005 1PP0 0 3a a031 60 0 4- 2286 .65 0M 03P7 .5a34点-31023M 100P00aMPa
5.以CD为基准线，沿反时针方向另取角度2 ，得一射线，与 圆交于G点 ,
6.按比例尺量出 , 值，即为单元体斜面上的正应力和剪
应力,
三.验证 , 的正确性
由应力圆可得：
y y yx
xy x
n
x x xy
yx y
B1 B O 2
G1' ,E
D(x, xy)
2 2 A1
C L A 1

材料力学第七章知识点总结

材料力学第七章知识点总结
研究应力状态的目的：找出一点处沿不同方向应力的变化
规律，确定出最大应力，从而全面考虑构件破坏的原因，建 立适当的强度条件。
材料力学
3、一点的应力状态的描述
研究一点的应力状态，可对一个 包围该点的微小正六面体——单 元体进行分析
在单元体各面上标上应力 各边边长 dx , dy , dz
——应力单元体
三、几个对应关系
点面对应——应力圆上某一点的坐标值对应着单元体某一截面
上的正应力和切应力；
y
σy
n
τ
H (σα ,τα )
τ yxHτ xy来自αxσx
(σy ,Dτyx)
2α A (σx ,τxy)
c
σ
σx +σ y
2
转向对应——半径旋转方向与截面法线的旋转方向一致； 二倍角对应——半径转过的角度是截面法线旋转角度的两倍。
α =α0
=
−2⎢⎡σ x
⎣
−σ y
2
sin 2α0
+τ xy
cos
2α
0
⎤ ⎥
⎦
=0
=
−2τ α 0
τα0 = 0
tg
2α 0
=
− 2τ xy σx −σ y
可以确定出两个相互垂直的平面——主平面，分别为
最大正应力和最小正应力所在平面。
主平面的方位
(α0 ; α0′ = α0 ± 900 )
主应力的大小
材料力学
四、在应力圆上标出极值应力
τ
τ max
x
R
O σ min
2α12α0A(σx ,τxy)
c
σ
σ
max
(σy ,τyx) D

刘鸿文《材料力学》(第5版)笔记和课后习题(含考研真题)详解-应力和应变分析强度理论(圣才出品)

刘鸿文《材料力学》(第5版)笔记和课后习题(含考研真题)详解-应力和应变分析强度理论(圣才出品)

OA1
= OC + CA1
= x
+ y 2
+
(
x
− y )2 2
+
2 xy
= max = 1
OB1
= OC − CB1
=
x
+ 2
y
−
(
x
− 2
y
)2
+
2 xy
= min
=2
b．确定主平面方位的方法
如图 7-3（b）（c）所示，将半径 CD 旋转 20 到 CA1 处，单元体 x 轴沿 20 旋转方向
图 7-2 应力圆 （2）应力圆的应用 ①应力圆与单元体应力间的关系 点面之间的对应关系：单元体某一面上的应力，必对应于应力圆上某一点的坐标； 夹角关系：圆周上任意两点所引半径的夹角等于单元体上对应两截面夹角的两倍，且两 者的转向一致。 ②求单元体上任一截面上的应力 从应力圆的半径 CD 按方位角 α 的转向转动 2α 得到半径 CE，圆周上 E 点的坐标就是
任意两个互相垂直的截面上的正应力之和为常数，即 + +90 = x + y 。
③最大切应力和最小切应力 切应力的大小
max min
=
x
− y 2
2
+ 2xy
=
1 2
(max
− min )
切应力极值所在截面方位角
tan
21
=
x − y 2 xy
最大和最小切应力所在平面与主平面的夹角为 45°，即1 = 0 + 45。
圣才电子书 十万种考研考证电子书、题库视频学习平台

第 7 章 应力和应变分析强度理论

二向应力状态分析的解析法

二向应力状态分析的解析法

二向应力状态分析的解析法二向应力状态分析的解析法[知识回顾]基本变形下的强度条件:(板书)FNmax1、拉压 ,,,[,]maxA 正应力强度条件Mmax2、弯曲 ,,,[,]maxW*FSsz ,,,[,]maxbIz3、扭转剪应力强度条件T,,,[,]max Wt[教学导入]特点:以上强度条件考虑了危险点上只有正应力或只有剪应力的情况，即单向应力状态;当考虑的点上既有正应力又有剪应力时，就不能用单向应力状态理论来建立强度条件，需要用强度理论来建立强度条件[新课教学]材料力学教案力学教研室于月民二向应力状态分析的解析法一、应力状态的概述(一)一点处的应力状态(ppt)1、不同截面上,各点的应力不同F2F ,,,,12AA2、横截面上正应力分析和切应力分析的结果表明:同一横截面上,不同点的应力各不相同，此即应力的点的概念。

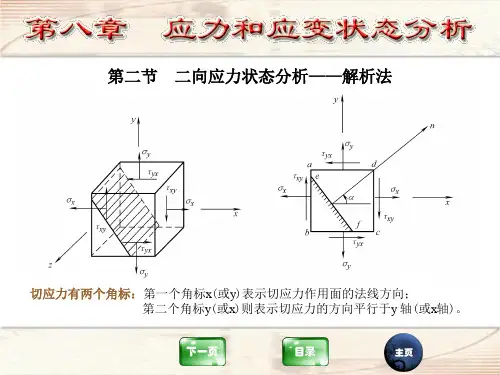
3、F横截面上: ,,,,0AF22,,cos,,,cos,,斜截面上: A,F,,sin2,,sin2,, 2A2同一点在不同方位截面上，它的应力也是各不相同的，此即应力的面的概念。

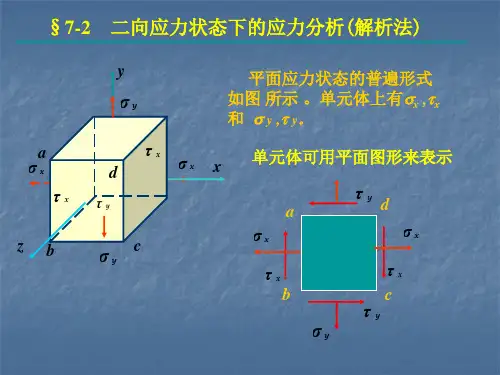
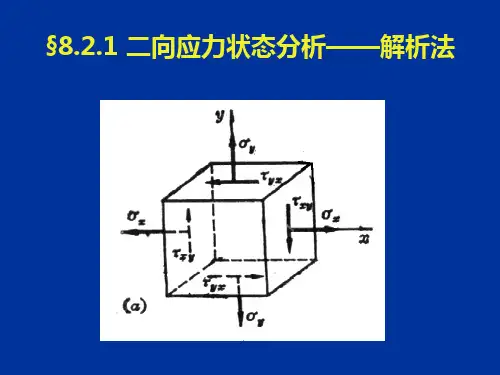
点的应力状态:(State of the Stresses of a Given Point)通过受力构件内某一点的不同方向面上的应力的集合，称之为这一点的应力状态1材料力学教案力学教研室于月民 (二)点的应力状态的表示(板书)1、单元体:围绕所考查的点，取三方向上尺寸无穷小的正六面体。

特点:1、各面上应力均匀分布2、相互平行的面上应力值相等如:轴向拉伸杆中过A取单元体，1)横、纵取F左右二面是杆横截面的一部分: ,,xA,,0上下和前后面都平行轴线:2)若与横纵成α角截取四个侧面与轴线即不平行也不垂直是斜截面，其上有正应力和剪应力2,,,cos,,x,x ,,sin2,,2由此可见:单元体的应力状态实质上代表一个点的应力状态，研究研究过一点的不同截面上应力变化情况，就是应力分析的内容。

取单元体的方位不同，表示出的形态不同，但二者等价。

材料力学--第2讲

材料力学--第2讲

所以：上述的9个应力分量就变成了6个应力分量
4、应力状态分类

三向应力状态：亦称空间应力状态，是最一般最复杂的； 二向应力状态：单元体只有两对面上承受应力并且作用线均在同一 平面内，另外一对面上没有任何应力，亦称平面应力状态；

单向应力状态：当平面应力状态中切应力为0，且只在一个方向上 有正应力作用时，称为——


而过一点各方向截面上应力矢量的集合称为该点的应
力状态。
2.3 一点的应力状态 切应力互等定律

1、单元体：（对连续均匀介质用极限的概念）来要描述构件上 一点a，就围绕a取一微小的六面体，当三个垂直的棱边趋近于0 时的极性时，即点a，称此微小六面体为——; 用截面外法线方向来命名截面，x面是指该截面的外法线法线沿x 轴，或者说该截面垂直于x轴；

斜面ABC上总应力矢量pn在x，y，在， 三个方向分量为：
pnx，pny，pnz，四面体处于平衡状态，在x轴方向则有：

斜面ABC上正应力
为总应力矢量pn在法线N上的投影，即是
pn的三个分量pnx，pny，pnz，在法线N上的投影的代数和：

2、主应力与主方向
过点O的斜面A*B*C*就是主平面，其方向余弦l* 、 m* 、 n*就是一 个主方向。因为主平面无切应力，则A*B*C*面上的全应力就是正 应力分量。该面上的全应力在坐标轴上的投影为：
△Ｐ
ｐ称为总应力或全应力。
应力求法
常用的表示方法是把p分解为两个分量:
垂直于截面的分量：正应力，用σ表示 沿截面的切向分量：切应力，用τ表示
正应力或法向应力σ : 剪应力或切应力τ :
总结：

Ｋ点的总应力p与截面方向有关。过Ｋ点在另外方向取 一截面，可定义另外一个不同的总应力矢量。过Ｋ点 可以有无限多个不同方向的截面，相应可得无限多个 不同的总应力矢量。 仅有一个方向截面的应力矢量，不能全面描述一点的 应力特性。

应力和应变状态培训讲学

应力和应变状态培训讲学
令 d 0 d
tg 21
x 2 xy
y
1
0
4
max
min
x
2
y
2
2 xy
4）两个导出公式：
max
min
m a x
m in
2
max min x y
例1. 已知如下单元体的应力状态，求图示斜截面上的应力和σmax、 σmin、τmax、τmin及主平面和最大剪应力所在平面的方位。
2
cos2 xy sin 2
22.2MPa
600
x
y
2
sin 2
xycos 2来自55MPa6）A点处的主应力及方位
max x y
min
2
x
2
y
2
2 xy
147.8 1.84MPa
1 147 .8MPa, 2 0, 3 1.84 MPa
tg 20
2 xy x y
解：
1）外力分析
RC
RB
P () 2
70kN
2) 内力分析(Q、M图)
3）A点横截面上的σ、τ
A
My IZ
146MPa
A
QASZ* bIZ
16.5MPa
4）在单元体上 x 146, xy A 16.5, 600, y 0
5）斜截面上的60°， 60°：
600
x y
2
x y
100 (80) sin 600 40cos600 2
97.64(MPa)
4）计算σmax、σmin及主平面方位角
max
min
x
y
2
x
2
y
2
2 xy

1.2应力状态解析法

1.2应力状态解析法

Ft 0
t dA s xdAcos sin t xydAcos cos
s ydAsin cos t yxdAsin sin 0
5
sy
考虑切应力互等和三角变换，得：
y
sx
txy
s
sx
sy
2
sx
s y
2
cos 2
t xy
sin 2
Ox
图1
s
sx
y
sy
ttyx
t
sx
s y
t xy
t
m Wp
t
求极值应力
t
y
Ox
s max s min
sx
sy
2
（s x
2
s
y
）2
t
2 xy
t2 xy
t
14
s1 t ;s 2 0;s 3 t
tg20
2t xy sx sy
-
0 -45
铸铁构件破坏分析
铸铁圆试样扭转试验时，正是沿着最大拉应 力作用面（即450螺旋面）断开的。因此，可 以认为这种脆性破坏是由最大拉应力引起的。
40
解：1）s x 60 s y －40 t xy 50
50 2）求主应力
60
s max s min
sx
sy
2
sx
s y
2
2
t
2 xy
80.7 60.7
（应力单位 MPa ） s1 80.7 s 2 0 s 3 60.7
11
3）求主方向
s3
s1
tg20
2t xy sx sy
1
0 22.5
0
s x s y 0为s max与x轴夹角

理论力学14应力状态分析

理论力学14应力状态分析


T
Wt

16M e πd3
联立解得扭转外力偶矩
Me

πd 3E45o
161

π
50103 3 210109
161 0.28
300 106
试求该扭转外力偶矩。
解： 在测点截取单元体
该点为纯剪切应力状态，与母线成45° 方向即为主方向，其主应力
1 2 0
根据广义胡克定律
3
45oBiblioteka 11 E
1

2
3

1
E
1
E

45o
1
E

圆轴表面的最大扭转切应力
2
MPa
80 MPa
第六节 广义胡克定律
一、二向应力状态下的胡克定律
x

1 E
x
y


y

1 E
y
x


二、三向应力状态下的胡克定律
x

1 E
x

y z


y

1 E
y

z
x


x


2
y
2


2 xy
切应力最大值
max

1
3
2
注意：切应力极大值不一定就是切应力最大值
四、纯剪切应力状态
1. 斜截面上的应力

sin 2
cos 2
2. 主平面和主应力
主平面： 45°斜截面
主应力： 1

第三强度理论.

第三强度理论.

第七章 应力和应变分析 强度理论§7.1应力状态概述过构件上一点有无数的截面，这一点的各个截面上应力情况的集合，称为这点的应力状态§7.2二向和三向应力状态的实例§7.3二向应力状态分析—解析法1．任意斜截面上的应力在基本单元体上取任一截面位置，截面的法线n 。

在外法线n 和切线t 上列平衡方程αασαατσc o s )c o s (s i n )c o s (dA dA dA x xy a -+0s i n )s i n (c o s )s i n (=-+αασαατdA dA y yxαασααττsin )cos (cos )cos (dA dA dA x xya --0sin )sin (cos )sin (=++ααταασdA dA yx y根据剪应力互等定理，yx xy ττ=，并考虑到下列三角关系 22sin 1sin ,22cos 1cos 22αααα-=+=，ααα2sin cos sin 2=简化两个平衡方程，得ατασσσσσα2sin 2cos 22xy yx yx --++=xyτyxτnαtατασστα2cos 2sin 2xy yx +-=2．极值应力将正应力公式对α取导数，得⎥⎦⎤⎢⎣⎡+--=ατασσασα2cos 2sin 22xy y x d d 若0αα=时，能使导数0=ασαd d ，则 02cos 2sin 200=+-ατασσxy yxyx xytg σστα--=220上式有两个解：即0α和 900±α。

在它们所确定的两个互相垂直的平面上，正应力取得极值。

且绝对值小的角度所对应平面为最大正应力所在的平面，另一个是最小正应力所在的平面。

求得最大或最小正应力为22min max )2(2xy y x yx τσσσσσσ+-±+=⎭⎬⎫ 0α代入剪力公式，0ατ为零。

这就是说，正应力为最大或最小所在的平面，就是主平面。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
自学提纲 一、 写出应力圆方程 并判断应力圆的圆心在那个轴上？
TSINGHUA UNIVERSITY
自学§7-4 二向应力状态分析-图解法
二、 应力圆的画法 1 定圆心 2 定半径 3 画圆 三、 应力圆的应用 1 求主应力 2 面内最大切应力
(1)
四、 几种特殊应力状态的应力圆
1：单向拉伸应力状态的应力圆 2 ：纯剪切应力状态的应力圆
y
dA - (dA cos ) sin - xy (dA cos ) cos x yx (dA sin ) sin y (dA sin ) cos 0
3、平面应力状态任意方向面上的正应力 与切应力 x y x - y cos2 - xysin2
二
主平面、主应力与主应力方向 x y x - y cos2 - xysin2 2 2

1
x - y
2
TSINGHUA UNIVERSITY
sin2 xy cos2
sin2 0 xy cos2 0 0
切应力为零的面为主平面
yx
x
y
左 右 面 上 的 切 应力
xy
x
各量的含义 1) 左右面上的正应力 上下面上的正应力 2 )
1 方向角与应力分量的正负号规定 正应力正负规定 拉应力为正压应力为负 切应力正负号规定
TSINGHUA UNIVERSITY
x y
' '
xy
yx
y
外法线
使微元或其局部顺时针方向转动为正； 反之为负
σ 0
σ
2 求正应力的极值面
x y

x - y
2 2 上式对α 求一次导数，并令其等于零
cos2 - xysin2
TSINGHUA UNIVERSITY
d -( x - y )sin2 - 2 xy cos2 0 d
解出的角度

TSINGHUA UNIVERSITY
- 90
yx
0
xy
y
即又一次证明了切应力的互等定理
二
主平面、主应力与主应力方向
1 切应力为零的面为主平面??
TSINGHUA UNIVERSITY
2 主应力 主平面上的正应力 ??
3 主应力方向 ------主平面的法线方向
要求 掌握主应力计算！！牢记公式，并进行 排序！
sin 2 xy cos 2
30
10 30 sin 60 20 cos 60 2
27.32MPa
思考 900 ？

90 ？？
0
x



用 斜截面截取，此截面上的应力为
2
TSINGHUA UNIVERSITY
y
dA
- x (dA cos ) cos xy (dA cos ) sin
- y (dA sin ) sin yx (dA sin ) cos 0
平衡方程
Ft 0
x


xy

t
n
TSINGHUA UNIVERSITY
yx
dA
方向角的正负号规定
由 x正向转到截面外法线
逆时针 为正 反之为负
注意：方向角的定义 以及正负号规定
n

x
TSINGHUA UNIVERSITY
问题
已知原始单元体互相垂直面上的应力
y yx
y
TSINGHUA UNIVERSITY
x
y
xy x x
求任意斜截面上的应力 （斜截面的位置？？）
yx

xy
y
x y x - y cos 2 xy sin 2 2 2
-
x - y
sin 2 - xy cos 2
90 x y
0

即单元体两个相互垂直面上 的正应力之和是一个常数
x


tan 2＝－
2 τ xy
x - y
角度α与α 0 完全重合。
表明∶ tan 2 0＝－ 正应力的极值面与主平面重合；
2 τ xy
x - y
正应力的极值就是主应力；
3 平面应力状态的三个主应力
解决问题的方法
平衡
的思想
2、单元体的局部平衡
y yx
y
n+
TSINGHUA UNIVERSITY
x

xy x x x
y

xy


n 0
????
+ 0
x


xy

t
n
TSINGHUA UNIVERSITY
yx
dA
2 2
TSINGHUA UNIVERSITY

x - y
2
sin2 xy cos2
y yx
y
x
y
xy x x
例题1求斜面ab上的正应力和切应力
y
20MPa
TSINGHUA UNIVERSITY
x 10MPa, y -30MPa 解：
a
xy 20MPa, yx -20MPa, 30

0
x - y
2
2 τ xy
tan 2 0＝－
x - y
0 0 90
O
该式确定了两个相互垂直的主平面的位置
对于平面应力状态， 平行于xy坐标面的平 面，其上既没有正应 力，也没有切应力作 用，前后面是一个主 平面。 这一主平面上的主应力等于零
σ
TSINGHUA UNIVERSITY
30

10MPa
300

x y
2

x - y
2
cos 2 - xy sin 2
b
30
0
20MPa
x

30
10 - 30 10 30 cos 60 - 20sin 60 2 2


x - y
2
30MPa
-17.32MPa
(1)
3：二向等拉应力状态的应力圆
§7-3 二向应力状态分析？？---解析法
主应力（计算）、主平面（位置确 定！）
----分析任意斜截面上的应力
任意斜截面上的应力
思路
一
TSINGHUA UNIVERSITY
要求： 1 掌握解决问题的思想
要求： 2 考研的同学理解记忆公式
y
TSINGHUA UNIVERSITY