二向应力状态分析
- 格式:ppt
- 大小:1.28 MB
- 文档页数:37







一般二向应力状态下求解主应力方法1.引言二向应力状态是指材料在受力情况下同时受到两个不同方向的应力作用。
在工程实践中,很多材料都会出现二向应力状态,因此如何准确求解在这种情况下的主应力是非常重要的。
本文将介绍一般二向应力状态下求解主应力的方法。
2.二向应力状态的概念在材料受力的情况下,如果同时存在两个不同方向的应力作用,就形成了二向应力状态。
一般来说,二向应力状态可以分为各向同性的和各向异性的两种情况。
各向同性是指材料在各个方向上的性能均相同,而各向异性则是指材料在不同方向上的性能存在差异。
在工程实践中,需要根据具体情况来判断材料的二向应力状态,以便正确求解主应力。
3.一般二向应力状态下求解主应力方法一般二向应力状态下求解主应力的方法可以分为数学方法和实验方法两种。
3.1 数学方法数学方法是通过数学推导和计算来求解主应力的方法。
在一般二向应力状态下,可以采用坐标变换的方法将二向应力状态转化为主应力状态。
具体步骤如下:(1)确定材料受力情况并获取二向应力状态的数值;(2)根据材料的各向同性或各向异性特点,选择合适的坐标系,进行坐标变换;(3)利用坐标变换后的应力矩阵,通过数学运算求解出主应力的数值。
3.2 实验方法实验方法是通过实验手段来求解主应力的方法。
在一般二向应力状态下,可以采用应变片法或光栅法来进行主应力的实验测量。
具体步骤如下:(1)利用应变片或光栅在材料表面进行应力测量;(2)根据实验测量结果,计算出主应力的数值。
4.应用举例为了更好地理解一般二向应力状态下求解主应力的方法,我们可以举一个具体的应用例子。
某种材料同时受到水平和垂直方向的应力作用,需要求解主应力。
可以采用数学方法进行坐标变换,将二向应力状态转化为主应力状态,再通过数学计算求解主应力的数值。
5.总结一般二向应力状态下求解主应力是工程实践中的重要课题。
通过数学方法和实验方法的结合,可以准确求解出材料在二向应力状态下的主应力,为工程设计和材料应用提供重要依据。
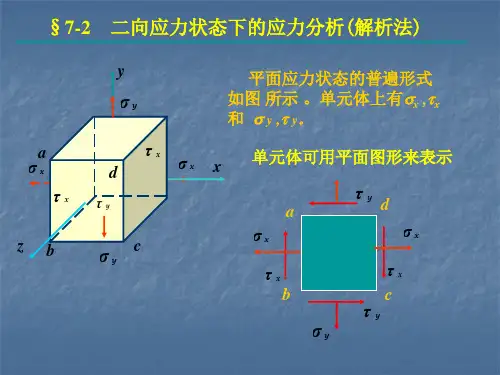
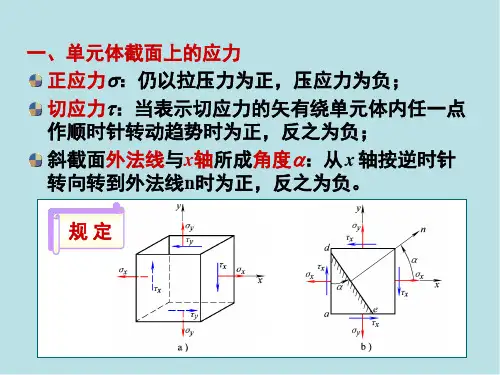
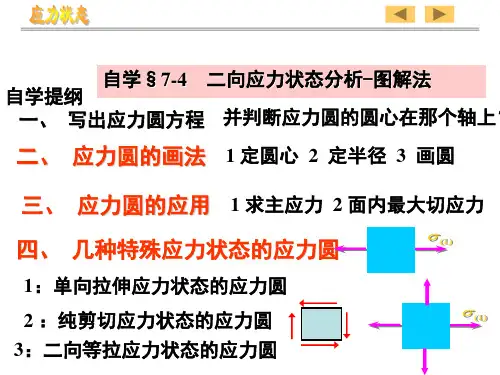
二向应力状态分析的解析法二向应力状态分析的解析法[知识回顾]基本变形下的强度条件:(板书)FNmax1、拉压 ,,,[,]maxA 正应力强度条件Mmax2、弯曲 ,,,[,]maxW*FSsz ,,,[,]maxbIz3、扭转剪应力强度条件T,,,[,]max Wt[教学导入]特点:以上强度条件考虑了危险点上只有正应力或只有剪应力的情况,即单向应力状态;当考虑的点上既有正应力又有剪应力时,就不能用单向应力状态理论来建立强度条件,需要用强度理论来建立强度条件[新课教学]材料力学教案力学教研室于月民二向应力状态分析的解析法一、应力状态的概述(一)一点处的应力状态(ppt)1、不同截面上,各点的应力不同F2F ,,,,12AA2、横截面上正应力分析和切应力分析的结果表明:同一横截面上,不同点的应力各不相同,此即应力的点的概念。
3、F横截面上: ,,,,0AF22,,cos,,,cos,,斜截面上: A,F,,sin2,,sin2,, 2A2同一点在不同方位截面上,它的应力也是各不相同的,此即应力的面的概念。
点的应力状态:(State of the Stresses of a Given Point)通过受力构件内某一点的不同方向面上的应力的集合,称之为这一点的应力状态1材料力学教案力学教研室于月民 (二)点的应力状态的表示(板书)1、单元体:围绕所考查的点,取三方向上尺寸无穷小的正六面体。
特点:1、各面上应力均匀分布2、相互平行的面上应力值相等如:轴向拉伸杆中过A取单元体,1)横、纵取F左右二面是杆横截面的一部分: ,,xA,,0上下和前后面都平行轴线:2)若与横纵成α角截取四个侧面与轴线即不平行也不垂直是斜截面,其上有正应力和剪应力2,,,cos,,x,x ,,sin2,,2由此可见:单元体的应力状态实质上代表一个点的应力状态,研究研究过一点的不同截面上应力变化情况,就是应力分析的内容。
取单元体的方位不同,表示出的形态不同,但二者等价。