六年级数学期中测试卷双向细目表

小学数学试题双向细目表小学数学试题双向细目表是一种用于指导小学数学教育评估的工具，它可以帮助教师根据学生的不同学习水平和能力，设计出更加精准、有效的数学试题。

本文将详细介绍小学数学试题双向细目表，并探讨其在小学数学教育评估中的应用。

一、小学数学试题双向细目表概述小学数学试题双向细目表是一种以表格形式呈现的评估工具，它根据数学课程的目标和内容，列出了不同层次和能力的学生在完成数学试题时应该掌握的知识点和技能。

通常，双向细目表包括三个维度：认知目标、知识点和难度等级。

认知目标维度指出了学生应该达到的认知水平，如理解、应用、分析等；知识点维度列出了试题中涉及到的数学知识点；难度等级维度则指出了试题的难易程度，以便教师根据学生的实际情况进行评估。

二、小学数学试题双向细目表的应用1、确定评估目标在进行数学评估时，教师需要明确评估的目标，即学生应该掌握的数学知识和技能。

双向细目表可以帮助教师确定评估目标，使其更加明确和具体。

在细目表中，教师可以根据知识点维度，列出学生需要掌握的数学概念、方法和技能，进而设计出相应的试题。

2、制定评估计划评估计划是教师进行数学评估的基础，它可以指导教师设计出更加全面、系统的数学试题。

在制定评估计划时，教师可以根据双向细目表，将知识点和难度等级进行分类和排序，然后根据学生的实际情况，制定出适合不同层次和能力学生的评估计划。

3、设计数学试题在设计数学试题时，教师需要根据双向细目表中的知识点和难度等级，结合学生的实际情况，设计出更加精准、有效的试题。

例如，教师可以根据知识点维度，设计出涵盖不同数学概念的试题；可以根据难度等级维度，设计出适合不同能力学生的试题。

4、进行评估和反馈在进行数学评估时，教师需要根据双向细目表对学生的表现进行评估，并根据评估结果进行反馈和指导。

通过双向细目表的指导，教师可以更加准确地了解学生的学习情况和问题，进而提出更加精准的建议和指导。

三、总结小学数学试题双向细目表是一种非常实用的评估工具，它可以帮助教师根据学生的实际情况，设计出更加精准、有效的数学试题。

小学数学单元测验双向细目表一、简介本文档旨在提供一份小学数学单元测验的双向细目表，帮助老师们对学生的研究情况有更清晰的了解。

通过此表，可以系统地记录学生的掌握程度，以便针对性地进行教学和辅导。

此外，双向细目表也可以作为学生和家长们了解研究进展的参考。

二、双向细目表格式说明1. 基本信息栏- 学生姓名：填写学生姓名- 学号：填写学生学号- 学年学期：填写学年和学期- 班级：填写学生所在班级2. 单元测验内容栏- 标题：填写测验的单元名称- 日期：填写测验日期3. 学生表现栏（逐个单元记录）- 项目：记录测验中的具体项目，如填空题、选择题等- 正确答案：填写该项目的正确答案- 学生答案：填写学生在测验中的答案，并标注是否正确4. 综合评价栏- 学生的优点：简要记录学生在本次测验中的亮点和优秀表现- 学生的不足：简要记录学生在本次测验中的不足之处和需要提升的地方- 改进建议：针对学生在本次测验中的不足，提出具体的改进和辅导建议三、使用方法1. 打开双向细目表模板，填写基本信息栏中的学生姓名、学号、学年学期和班级。

2. 在单元测验内容栏中填写测验的单元名称和日期。

3. 在学生表现栏中按照测验内容逐个记录学生的答案。

4. 在综合评价栏中给出学生的优点、不足和改进建议。

5. 根据需要，可以复制多份学生表现栏，记录多位学生的情况。

四、注意事项1. 确保填写的学生基本信息准确无误，以免造成混淆。

2. 在记录学生答案时，标注正确与否，便于后期统计与分析。

3. 综合评价栏中的优点、不足和改进建议要具体明确，便于学生和家长们理解并采取行动。

4. 定期更新和归档测验记录，方便跟踪研究进展和进行后续的教学辅导。

5. 鼓励学生根据综合评价栏中的改进建议，针对不足进行反思和努力提高。

五、总结通过使用此双向细目表，我们可以更好地了解学生在数学研究中的掌握情况，分析研究缺失点，为学生提供有针对性的辅导。

同时，学生和家长们也可以通过综合评价栏了解研究进展和改进方向。

六年级单元测验双向细目表
假定：
该单元由3个小主题组成。

本张试卷的题型为：选择题、辨析题、填空题、习作题。

其中：
选择题：25道。

每题1分，共25分
判断题：5道。

每题1分，共5分
填空题：25道，每题2分，共50分
习作题：2道，每题10分，共20分
【注】表中数字斜杠左边为题数，斜杠右边为分数。

如果按该表出试卷：
一、做到全覆盖。

二、重点在主题1和主题2（这两主题分别出22、23道题，占32、42分，比重最大）。

二、中等难度的题比重较大。

题数和所占分数都多于难题和容易的题。

三、容易题和中等难度的题相比，容易题所占分值少了一些。

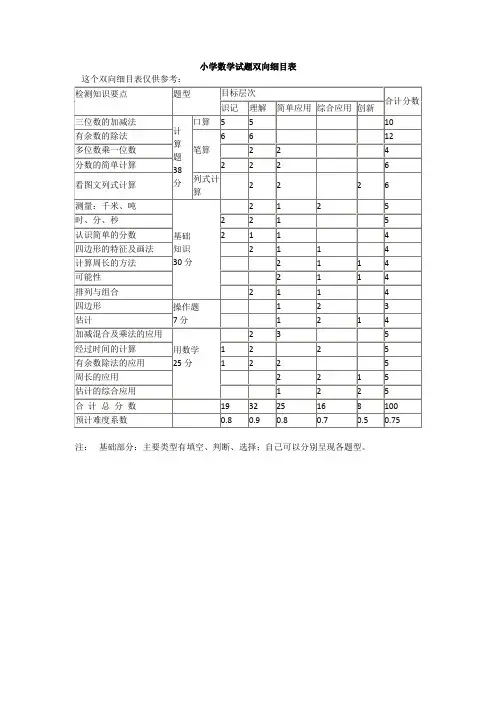
单元测验双向细目表（参考样例）
假定：
一、该单元由六个小主题组成。

二、本张试卷的题型为：计算题、填空题、选择题、辨析题、案例分析题。

1.计算题：7道，每小题4分，共18分，合计28分
2.填空题：10道，每空1分，共21分
3.选择题：6道，每题2分，共12分
4.辨析题：5道。

每题1分，共5分
5.看图列式计算：2道，每小题2分，共4分
6.案例分析题：6道，每题5分，共30分
【注】表中数字斜杠左边为题数，斜杠右边为分数。

如果按该表出试卷：
一、做到全覆盖。

二、重点在主题四和主题五。

二、中等难度的题比重较大。

题数和所占分数都多于难题和容易的题。

三、难题和容易的题相比，容易的题所占分值适当，必要时可适当调整。

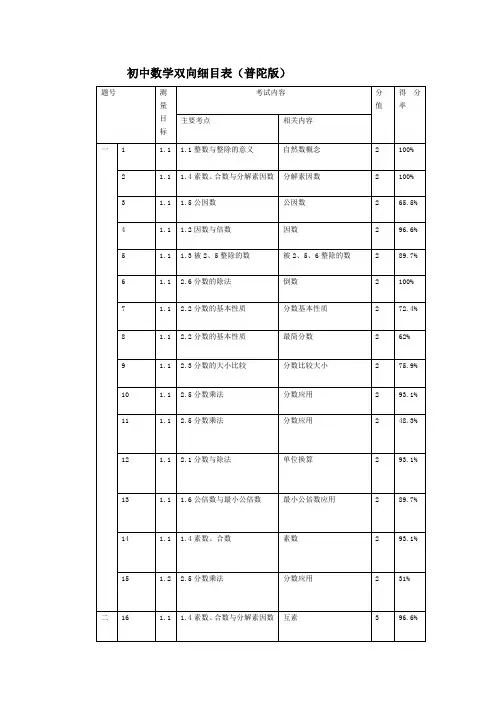
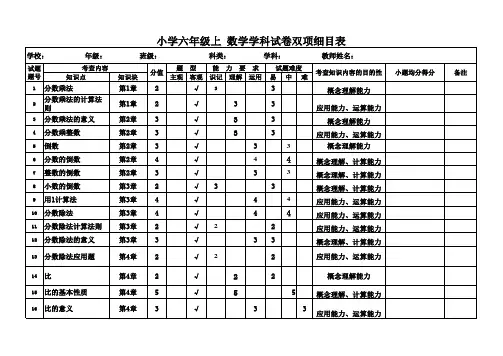
2 3等于乙数的75%（甲、乙都不为0），那么（）7.如果甲的2020—2021年度第二学期小学数学六年级下册期中检测试题命题双向细目表年级: 六年级下册 科目：数学 命题人： 时间：2021年3月17日题 型题号分值内容领域具体内容了解理解掌握运用难易程度分值易中难选择11数与代数数大小比较√121数与代数比的表示√131空间与图形几何图形的面积√141数与代数百分数的应用√151数与代数分数乘除法√161空间与图形三视图的认识√171数与代数数的比较√181统计与概率统计图的选择√191数与代数比例的意义√1101数与代数负数的意义√1111空间与图形圆锥的体积√1 121空间与图形圆柱与圆锥的体积√1 131数与代数连续百分数应用√1141数与代数工程问题√1填空14数与代数 大数的读写√423数与代数 单位换算√3 31数与代数比、分数、除法、百分数转换√1 41数与代数圆的周长面积√1 52数与代数 分数的意义√2 62空间与图形百分数的应用√2 72数与代数 分率的求法√2 82数与代数等底等高圆柱圆锥体积关系应用√2 91数与代数 数的大小比较√1 102数与代数 比例的性质√2 10.5数与代数整数加减√0.530.5数与代数百分数乘法√0.5 40.5数与代数分数除法√0.5 50.5数与代数分数减法√0.5 60.5数与代数分数乘法√0.5 70.5数与代数估算√0.5 80.5统计与概率分数减法√0.5 90.5数与代数小数乘方√0.5 100.5数与代数百分数乘法√0.5计算题2①3数与代数 分数加减简算√3②3数与代数乘法分配律（分数）√3③3数与代数乘法分配律（分数）√3④3数与代数 混合运算√3计算题3①2数与代数 解方程√2②2数与代数 解方程√2③2数与代数 解方程√2列式计算①3数与代数 列式计算3②3数与代数 列式计算3解决问题15数与代数百分数应用题√525数与代数比例的应用 √535空间与图形圆柱表面积应用√5 45数与代数百分数的应用√5 55空间与图形公式的运用√565数与代数方程的应用√5拓展题12数与代数比的应用√√2 2数与代数解题策略√合计9535564计算题1。

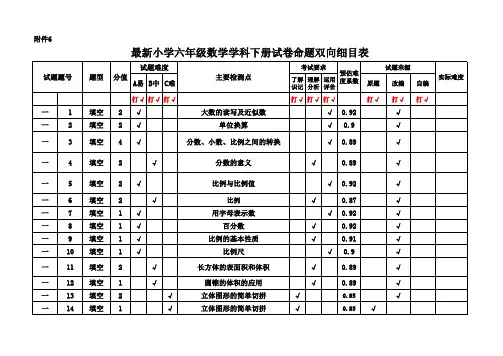
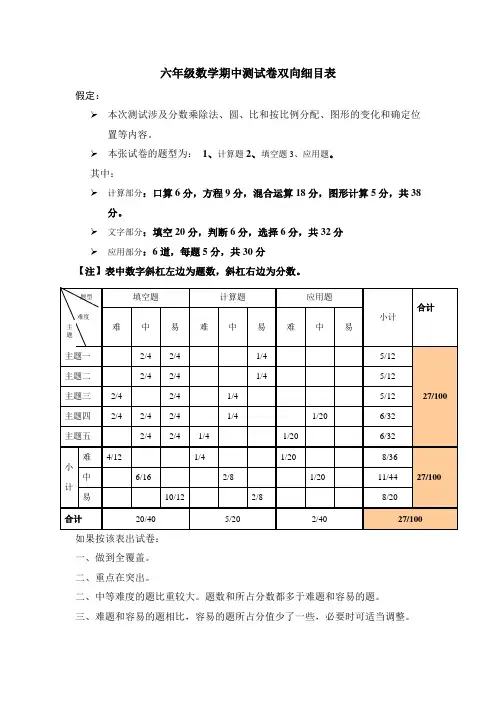
六年级数学期中测试卷双向细目表
假定：
本次测试涉及分数乘除法、圆、比和按比例分配、图形的变化和确定位置等内容。

本张试卷的题型为：1、计算题2、填空题3、应用题。

其中：
计算部分：口算6分，方程9分，混合运算18分，图形计算5分，共38分。

文字部分：填空20分，判断6分，选择6分，共32分
应用部分：6道，每题5分，共30分
【注】表中数字斜杠左边为题数，斜杠右边为分数。

如果按该表出试卷：
一、做到全覆盖。

二、重点在突出。

二、中等难度的题比重较大。

题数和所占分数都多于难题和容易的题。

三、难题和容易的题相比，容易的题所占分值少了一些，必要时可适当调整。

数学试卷及双向细目表试卷题号题型分值一二12345678911112131415161718192选择题填空题4444444444444444441111三2122232425解答题121214试题难度A 易B 中C 难√√√√√√√√√√√√√√√√√√√√√√√√√学段、板块主要知识及主要思想方法七年级“整式”单项式乘以单项式、幂的运算法则六年级“一次方程” 方程根的意义、解一元一次方程八年级“函数”一次函数图像八年级”向量”向量八年级“概率”概率九年级”向量”向量六年级“一次不等式”一元一次不等式的解集七年级“整式”八年级“方程”八年级“方程”八年级“函数”利用平方差公式因式分解换元法无理方程的解函数值八年级“反比例函数”反比例函数、待定系数法八年级“一次函数” 一次函数、图形运动(平移)九年级“统计”统计七年级“平行直线”平行线性质九年级“相似三角形”相似三角形的性质九年级“相似三角形”平行线分线段成比例、平行四边形的性质九年级“锐角三角比”三角比、点和圆的位置关系“圆”八年级“二次根式” 二次根式的化简、分母有理化八年级“分式方程“ 分式方程、转化思想九年级“三角比“”锐角三角比、垂径定理、方程思想圆“九年级“统计” 图表信息处理八年级“几何证明” 特殊四边形的证明九年级“二次函数” 二次函数、待定系数法、配方法、数形结合思想等综合题三角形面积、圆与圆位置关系、相似三角形、函数思想等。