2017-2018学年高中数学苏教版选修2-3 课下能力提升(十一)超几何分布Word版 含解析

2.2 超几何分布超几何分布一般地，若一个随机变量X 的分布列为P (X ＝r )＝C r M C n －rN －MC n N，其中r ＝0,1,2,3，…，l ，l＝min(n ，M )，则称X 服从超几何分布．记为X ～H (n ，M ，N )，并将P (X ＝r )＝C r M C n －r N －MC n N记为H (r ；n ，M ，N )．预习交流如何正确理解超几何分布？提示：设有N 件产品，其中有M (M ≤N )件次品，从中任取n (n ≤N )件产品，取出的产品中有r 件次品的概率为P (X ＝r )＝C r M C n －r N －MC n N(其中r 为非负整数)，此时随机变量X 服从参数为N ，M ，n 的超几何分布．一、超几何分布的实例某班共50名学生，其中35名男生，15名女生，随机从中抽取5名同学参加学生代表大会，所抽取的5名学生代表中，求女生人数X 的分布列．思路分析：由题意知女生人数X 服从超几何分布H (5,15,50)． 利用超几何分布的概率公式求解．解：从50名学生中随机抽取5人共有C 550种方法，没有女生的取法是C 015C 535，恰有1名女生的取法为C 115C 435，恰有2名女生的取法为C 215C 335，恰有3名女生的取法为C 315C 235，恰有4名女生的取法为C 415C 135，恰有5名女生的取法为C 515C 035.下列随机变量中，服从超几何分布的有__________．①一批产品50箱，其中有2箱不合格，从该批产品中任取5箱产品进行检测，其中不合格的产品箱数X .②一个盆子里有4个红球和3个黑球，从中任取一个球，然后放回，连续三次，记取到红球的个数为X .答案：①解析：①X 服从超几何分布H (5,2,50)；②不服从超几何分布，因为它是有放回地抽样． 判断一个随机变量是否服从超几何分布，主要是根据定义，注意超几何分布是不放回的取样．二、超几何分布的实际应用从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试．试求出选3名同学中，至少有一名女同学的概率．思路分析：由题目可知选出的女同学人数服从超几何分布H (3,4,10)，根据超几何分布概率公式直接求，也可用间接法求解．解：设选出的女同学人数为X ，则X 的可能取值为0,1,2,3，且X 服从超几何分布H (3,4,10)，于是选出的3名同学中，至少有一名女同学的概率为：P (X ≥1)＝P (X ＝1)＋P (X＝2)＋P (X ＝3)＝C 14C 26C 310＋C 24C 16C 310＋C 34C 06C 310＝56，或P (X ≥1)＝1－P (X ＝0)＝1－C 04C 36C 310＝56.一批产品共50件，其中5件次品，45件合格品，从这批产品中任意抽2件，求其中出现次品的概率．解：设抽到次品的件数为X ，则X 服从超几何分布H (2,5,50)．于是出现次品的概率为P (X ≥1)＝P (X ＝1)＋P (X ＝2)＝C 15C 2－150－5C 250＋C 25C 2－250－5C 250＝949＋2245＝47245，即出现次品的概率为47245.①超几何分布是一种常见的随机变量的分布，利用它可解决一类超几何分布问题． ②在超几何分布中，只要知道参数N ，M ，n 就可以根据公式求出X 取不同值时的概率．从而列出分布列，再求符合题意的概率．1．有10件产品，其中3件是次品，从中任取2件，若X 表示取得次品的个数，则P (X ＜2)＝__________.答案：1415解析：由题意知X 可取0,1,2，服从超几何分布H (2,3,10)，即P (X ＜2)＝P (X ＝0)＋P (X ＝1)＝C 03C 27C 210＋C 13C 17C 210＝715＋715＝1415.2．100张奖券中有4张有奖，从这100张奖券中任取2张，则2张都中奖的概率为__________．答案：1825解析：由题意知X 可取0,1,2且服从超几何分布H (2,4,100)．所以2张都中奖的概率为P (X ＝2)＝C 24C 096C 2100＝1825.3．把X ，Y 两种遗传基因冷冻保存，若X 有30个单位，Y 有20个单位，且保存过程中有2个单位的基因失效，则X ，Y 两种基因各失效1个单位的概率是__________．答案：2449解析：由题意可设遗传基因X 失效单位的个数为ξ，则ξ服从超几何分布H (2,30,50)．则X ，Y 两种基因各失效1个单位的概率为P (ξ＝1)＝C 130C 120C 250＝2449.4．从3台甲型彩电和2台乙型彩电中任选2台，其中两种型号都齐全的概率为__________．答案：35解析：由题意可设随机变量X 表示“选出的彩电中乙型彩电的台数”，则X 服从超几何分布H (2,2,5)．则两种型号都齐全的概率为P (X ＝1)＝C 13C 12C 25＝35.5．50张彩票中只有2张中奖票，今从中任取n 张，为了使这n 张彩票里至少有一张中奖的概率大于0.5，n 至少为多少？解：设随机变量X 表示“抽出的中奖票的张数”，则X 服从超几何分布H (n,2,50)．∴P (X ≥1)＝P (X ＝0)＋P (X ＝1)＝C 12C n －148C n 50＋C 22C n －248C n 50＞0.5.解得n ≥15.∴n 至少为15时，至少有一张中奖的概率大于0.5.。

超几何分布
教学目标 知识与技能：通过实例，理解超几何分布及其特点。

过程与方法：掌握超几何分布列及其导出过程。

情感、态度与价值观：通过对实例的分析，会进行简单的应用。

教学重难点 超几何分布的理解，分布列的推导。

教具准备：与教材内容相关的资料。

教学设想：引导学生形成 “自主学习”与“合作学习”等良好的学习方式。

教学过程：
学生探究过程：
问题情境
假定一批产品共100件，其中有5件不合格品，随机取出的10件产品中，不合格品数X 的概率分布如何？并将所得到的结果推广到一般的情况，能得到什么结果。

构建数学 一般地，若一个随机变量X 的分布列为 ,n
N
C r
n M N C r M C r)P(X --==① 其中r=0，1，2，…，l,l=min(n,M ), 则称X 服从超几何分布，记为X ～Ｈ（n,M,N ）,并将①记为Ｈ（r;n,M,N ）.
数学应用
例1、高三（1）班联欢会上设计了一项游戏：在一个口袋中装有10个红球，20个白球，这些
球除颜色外完全相同，一次从中摸出5个球，摸到4个红球1个白球的就中一等奖。

求中一等奖的概率。

例2、生产方提供50箱的一批产品，其中有2箱不合格产品。

采购方接收该批产品的准则是：从该批产品中任取5箱产品进行检测，若至多有1箱不合格品，便接收该批产品。

问：该批产品被接受的概率是多少？
教学反思：
1. 通过实例，理解超几何分布及其特点。

2. 掌握超几何分布列及其导出过程。

3. 通过对实例的分析，会进行简单的应用。

超几何分布教学目标1．通过实例，理解超几何分布及其特点；2．通过对实例的分析，掌握超几何分布列及其导出过程，并能简单的应用． 教学重点，难点:理解超几何分布的概念，超几何分布列的应用． 教学过程 一．问题情境 1．情境：在产品质量管理中，常常通过抽样来分析合格品和不合格品的分布，进而分析产品 质量．假定一批产品共N 件，其中有M 件不合格品，随机取出的n 件产品中，不合格品数X 的概率分布如何？ 2．问题：用怎样的数学模型刻画上述问题？ 二．学生活动以100N =，5M =，10n =为例，研究抽取10件产品中不合格品数X 的概率分布．三．建构数学从100件产品中随机抽取10件有10100C 种等可能基本事件．{}2X =表示的随机事件是“取到2件不合格品和8件合格品”，依据分步计数原理有28595C C 种基本事件，根据古典概型， 2859510100(2)C C P X C ==．类似地，可以求得X 取其他值时对应的随机事件的概率，从而得到不合格Xn 件其中min(,)l n M =．一般地，若一个随机变量X 的分布列为()r n r M N MnNC C P X r C --==， 其中0r =，1，2，3，…，l ，min(,)l n M =，则称X 服从超几何分布，记为(,,)X H n M N ，并将()r n r M N MnNC C P X r C --==记为(;,,)H r n M N ． 说明：（1）超几何分布的模型是不放回抽样； （2）超几何分布中的参数是M ，N ，n ． 四．数学运用 1．例题：例1．高三（1）班的联欢会上设计了一项游戏：在一个口袋中装有10个红球，20个白球，这些球除颜色外完全相同．现一次从中摸出5个球， （1）若摸到4个红球1个白球的就中一等奖，求中一等奖的概率． （2）若至少摸到3个红球就中奖，求中奖的概率．解：（1）若以30个球为一批产品，其中红球为不合格产品，随机抽取5个球，X 表示取到的红球数，则X 服从超几何分布(5,10,30)H ．由公式得4541020530700(4;5,10,30)0.029523751C C H C -==≈， 所以获一等奖的概率约为2.95%．（2）根据题意，设随机变量X 表示“摸出红球的个数”，则X 服从超几何分布(5,10,30)H ，X 的可能取值为0，1，2，3，4，5，根据公式可得至少摸到3个红球的概率为：324150102010201020555303030(3)(3)(4)(5)0.1912C C C C C C P X P X P X P X C C C ≥==+=+==++≈， 故中奖的概率为0.1912．例2．生产方提供50箱的一批产品，其中有2箱不合格产品．采购方接收该批产品的准则是：从该批产品中任取5箱产品进行检测，若至多有1箱不合格产品，便接收该批产品．问：该批产品被接收的概率是多少？解：以50箱为一批产品，从中随机抽取5箱，用X 表示“5箱中不合格产品的箱数”，则X 服从超几何分布(5,2,50)H ．这批产品被接收的条件是5箱中没有不合格的箱或只有1箱不 合格，所以被接收的概率为(1)P X ≤，即0514248248555050243(1)245C C C C P X C C ≤=+=． 答：该批产品被接收的概率是243245（约为0.99184）． 说明：（1）在超几何分布中，只要知道N 、M 和n ，就可以根据公式，求出X取不同m 值时的概率()P X m =，从而列出X 的分布列．（2）一旦掌握了X 的分布列，就可以算出相应试验的很多事件的概率，从而就完全掌握了该试验．思考：该批产品中出现不合格产品的概率是多少？例3．50张彩票中只有2张中奖票，今从中任取n 张，为了使这n 张彩票里至少有一张中奖的概率大于0.5，n 至少为多少？解：设随机变量X 表示“抽出中奖票的张数”，则X 服从超几何分布(,2,50)H n ，根据公式可得至少有一张中奖的概率11222482485050(1)0.5n n n nC C C C P X C C --≥=+>，解得15n ≥．答：n 至少为15张． 五．回顾小结：1．超几何分布的特点； 2．超几何分布列的简单应用．。

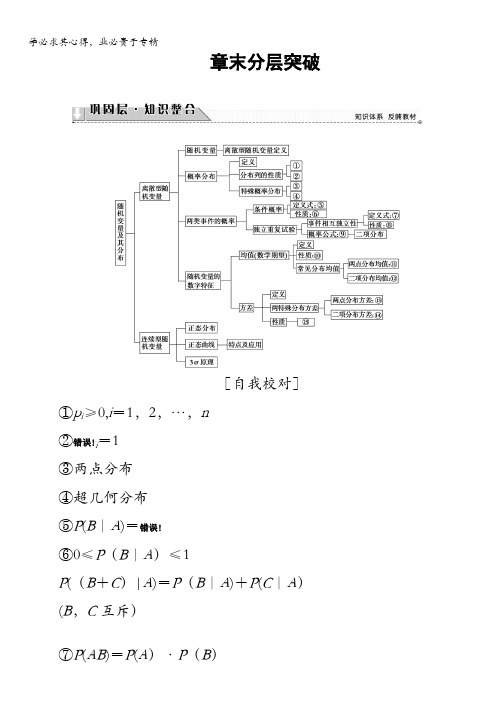
章末分层突破［自我校对］①p i≥0,i＝1，2，…，n②错误!i＝1③两点分布④超几何分布⑤P(B｜A)＝错误!⑥0≤P（B｜A）≤1P(（B＋C）|A)＝P（B｜A)＋P(C｜A）(B，C互斥）⑦P(AB)＝P(A）·P（B）⑧A与B相互独立，则错误!与B，A与错误!，错误!与错误!相互独立⑨P(X＝k）＝C错误!p k（1－p)n－k(k＝0，1,2，…,n）⑩E（aX＋b)＝aE(X)＋b⑪E(X）＝p⑫E(X)＝np⑬V（X）＝p（1－p)⑭V(X)＝np（1－p）⑮V(aX＋b）＝a2V（X)条件概率条件概率是学习相互独立事件的前提和基础,计算条件概率时，必须搞清欲求的条件概率是在什么条件下发生的概率．求条件概率的主要方法有：利用条件概率公式P(B|A)＝错误!计算．在5道题中有3道理科题和2道文科题．如果不放回地依次抽取2道题,求:(1）第1次抽到理科题的概率;（2）第1次和第2次都抽到理科题的概率；（3)在第1次抽到理科题的条件下，第2次抽到理科题的概率．【精彩点拨】本题是条件概率问题，根据条件概率公式求解即可．【规范解答】设“第1次抽到理科题”为事件A，“第2题抽到理科题"为事件B，则“第1次和第2次都抽到理科题”为事件AB.（1)从5道题中不放回地依次抽取2道题的事件数为n(Ω）＝A25＝20。

根据分步计数原理，n（A)＝A错误!×A错误!＝12。

于是P(A)＝错误!＝错误!＝错误!.(2）因为n（AB）＝A错误!＝6,所以P（AB）＝错误!＝错误!＝错误!。

(3)由(1）（2）可得，在第1次抽到理科题的条件下，第2次抽到理科题的概率P(B｜A)＝错误!＝错误!＝错误!。

［再练一题]1．掷两颗均匀的骰子,已知第一颗骰子掷出6点,问“掷出点数之和大于或等于10”的概率．【解】设“掷出的点数之和大于或等于10"为事件A，“第一颗骰子掷出6点”为事件B。

2.2 超几何分布学案（苏教版高中数学选修2-3）2.2超几何分布超几何分布学习目标1.了解超几何分布的实际背景.2.理解超几何分布的特征.3.能用超几何分布这一概率模型解决相关问题知识点超几何分布思考从4名男生和2名女生中任选3人参加演讲比赛，设随机变量X 表示所选3人中女生的人数1X的所有可能值是什么2X的概率分布是什么答案10,1,2.2PX0C34C3642021，PX1C12C24C36122035，PX2C22C14C3642021，X的概率分布如下表X012P153515梳理超几何分布1概念一般地，若一个随机变量X的分布列为PXrCrMCnrNMCnN，其中r0,1,2,3，，l，lminn，M，则称X服从超几何分布2记法X服从超几何分布，记为XHn，M，N，并将PXrCrMCnrNMCnN记为Hr；n，M，N3含义在Hr；n，M，N中，r，n，M，N的含义特别提醒1超几何分布的模型特点超几何分布中的正品.次品也可以理解为黑.白，男.女等有明显差异的两部分超几何分布中“Xk”的含义是“取出的n件产品中恰好有k件次品”2超几何分布的特征超几何分布的抽取是不放回的超几何分布本质上还是这一事件在该随机试验中发生的次数与总次数的比1超几何分布就是一种概率分布模型2一个袋子里装有4个白球，5个黑球和6个黄球，从中任取4个球，则所拿黑球个数X就服从超几何分布3超几何分布中，只要知道M，N，n，就可以利用公式求出X取不同k的概率PXk，从而求出X的分布列类型一超几何分布求概率例1从放有10个红球与15个白球的暗箱中，随意摸出5个球，规定取到一个白球得1分，一个红球得2分，求某人摸出5个球，恰好得7分的概率考点题点解设摸出的红球个数为X，则X 服从超几何分布，其中N25，M10，n5.由于摸出5个球，得7分，仅有两个红球的可能，那么恰好得7分的概率为PX2C210C315C5250.385，即恰好得7分的概率约为0.385.反思与感悟解答此类问题的关键是先分析随机变量是否满足超几何分布若满足，则直接利用公式解决；若不满足，则应借助相应概率公式求解跟踪训练1在元旦晚会上，数学老师设计了一个摸奖游戏，在一个口袋中装有10个红球和20个白球，这些球除颜色外完全相同，从中任意摸出5个球，至少摸到3个红球中奖，求中奖的概率结果保留两位小数考点题点解设摸出红球的个数为X，则X服从超几何分布，其中N30，M10，n5.于是中奖的概率为PX3PX3PX4PX5C310C533010C530C410C543010C530C510C553010C530 1xx021020252C530272521425060.19.类型二超几何分布求概率分布例2一个袋中装有6个形状大小完全相同的小球，其中红球有3个，编号_________为1,2,3；黑球有2个，编号_________为1,2；白球有1个，编号_________为1.现从袋中一次随机抽取3个球1求取出的3个球的颜色都不相同的概率；2记取得1号球的个数为随机变量X，求随机变量X的概率分布考点超几何分布题点求超几何分布的概率分布解1从袋中一次随机抽取3个球，基本事件总数nC3620，取出的3个球的颜色都不相同包含的基本事件的个数为C13C12C116，所以取出的3个球的颜色都不相同的概率为P620310.2由题意知，X0,1,2,3.PX0C33C36120，PX1C13C23C36920，PX2C23C13C36920，PX3C33C36120.所以X的概率分布为X0123P120920920120引申探究在本例条件下，若记取到白球的个数为随机变量，求随机变量的概率分布解由题意可知0,1，服从两点分布又P1C25C3612，所以的概率分布如下表01P1212反思与感悟超几何分布的求解步骤1辨模型结合实际情景分析所求概率分布问题是否具有明显的两部分组成，如“男生.女生”，“正品.次品”“优劣”等，或可转化为明显的两部分具有该特征的概率模型为超几何分布模型2算概率可以直接借助公式PXrCrMCnrNMCnN求解，也可以利用排列组合及概率的知识求解，需注意借助公式求解时应理解参数M，N，n，r 的含义3列分布表把求得的概率值通过表格表示出来跟踪训练2从5名男生和3名女生中任选3人参加奥运会火炬接力活动若随机变量X表示所选3人中女生的人数，求X的概率分布及PX2考点超几何分布题点求超几何分布的概率分布解由题意分析可知，随机变量X服从超几何分布，其中N8，M3，n3.所以PX0C35C03C38528，PX1C25C13C381528，PX2C15C23C381556，PX3C05C33C38156.故随机变量X的概率分布如下表X0123P52815281556156所以PX2PX0PX1528152857.类型三超几何分布的综合应用例3在10件产品中，有3件一等品，4件二等品，3件三等品从这10件产品中任取3件求1取出的3件产品中一等品件数X的概率分布；2取出的3件产品中一等品件数多于二等品件数的概率考点超几何分布题点求超几何分布的概率分布解1由于从10件产品中任取3件的基本事件总数为C310，从10件产品中任取3件，其中恰有m0m3且mN件一等品的基本事件个数为Cm3C3m7，那么从10件产品中任取3件，其中恰有m件一等品的概率为PXmCm3C3m7C310，m0,1,2,3.所以随机变量X的概率分布如下表X0123P724214074011202设“取出的3件产品中一等品件数多于二等品件数”为事件A，“恰好取出1件一等品和2件三等品”为事件A1，“恰好取出2件一等品”为事件A2，“恰好取出3件一等品”为事件A3.由于事件A1，A2，A3两两互斥，且AA1A2A3，又因为PA1C13C23C310340，PA2PX2740，PA3PX31120，所以PAPA1PA2PA3340740112031120.即取出的3件产品中一等品的件数多于二等品的件数的概率为31120.反思与感悟识别超几何分布的三大标准1总数为N件的物品只分为两类MMN件甲类或次品，NM件乙类或正品2从N件物品中行取nnN件物品必须采用不放回抽样3随机变量X表示从N件物品中任取nnN件物品，其中所含甲类物品或次品的件数跟踪训练3袋中装着标有数字1,2,3,4,5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性相等，用X表示取出的3个小球上的最大数字，求1取出的3个小球上的数字互不相同的概率；2随机变量X的概率分布；3计算介于20分到40分之间的概率考点题点解1“一次取出的3个小球上的数字互不相同”的事件记为A，则PAC35C12C12C12C31023.2由题意知，X所有可能的取值为2,3,4,5.PX2C22C12C12C22C310130，PX3C24C12C14C22C310215，PX4C26C12C16C22C310310，PX5C28C12C18C22C310815，所以随机变量X的概率分布如下表X2345P1302153108153“一次取球得分介于20分到40分之间”记为事件C，则PCPX3PX42153101330.1盒中有4个白球，5个红球，从中任取3个球，则取出1个白球和2个红球的概率是________考点题点答案1021解析设随机变量X为抽到白球的个数，X服从超几何分布，由公式，得PX1C14C25C39410841021.2由12名志愿者组成的医疗队中，有5名共产党员，现从中任选6人参加抗洪抢险，用随机变量X表示这6人中共产党员的人数，则PX3________.答案2566解析由题意知，XH6,5,12，PX3C35C37C6122566.3有10位同学，其中男生6位，女生4位，从中任选3人参加数学竞赛用X表示女生人数，则概率PX2________.考点题点答案2930解析PX2PX1PX2PX0C14C26C310C24C16C310C36C3102930.4从4名男生和2名女生中任选3人参加数学竞赛，则所选3人中，女生的人数不超过1人的概率为________考点超几何分布题点利用超几何分布求概率答案45解析设所选女生数为随机变量X，则X服从超几何分布，所以PX1PX0PX1C02C34C36C12C24C3645.5从1,2,3,4,5中任取3个数，记最大的数为，则P4________.考点题点答案310解析P4C11C23C35310.1超几何分布的判断判断随机变量是否服从超几何分布，可以从以下两个方面判断一是超几何分布描述的是不放回抽样问题；二是随机变量为抽到的某类个体的个数2超几何分布的分布列的求法1在超几何分布中，只要知道N，M和n，就可以根据公式，求出X取不同r值时的概率PXr，从而列出X的概率分布2一旦掌握了X的概率分布，就可以算出相应试验的很多事件的概率，从而就完全掌握了该试验。

2.2超几何分布[对应学生用书P28]从4名男生和2名女生中任选3人参加演讲比赛，设随机变量X 表示所选3人中女生的人数．问题1：X 的取值有哪些？ 提示：X ＝0,1,2问题2：X 的概率分布是什么？提示：P (X ＝0)＝C 02C 34C 36＝15，P (X ＝1)＝C 12C 24C 36＝35，P (X ＝2)＝C 22C 14C 36＝15.∴X 的概率分布为X 0 1 2 P153515问题3：“所选3人中，女生人数X ≤1”的概率是多少？ 提示：P (X ≤1)＝P (X ＝0)＋P (X ＝1)＝451．超几何分布的概念一般地，若一个随机变量X 的分布列为P (X ＝r )＝C r M C n －r N －MC n N，其中r ＝0,1,2,3，…，l ，l ＝min(n ，M )，则称X 服从超几何分布，记为X ～H (n ，M ，N )，并将P (X ＝r )＝C r M C n －rN －MC n N记为H (r ；n ，M ，N )．2．H (r ；n ，M ，N )中，r ，n ，M ，N 的含义1．超几何分布是概率分布的一种形式，一定要注意公式中字母的范围及其意义，解决问题时可以直接利用公式求解，但不能机械的记忆．2．超几何分布中，只要知道M ，N ，n 就可以利用公式求出X 取不同r 的概率P (X ＝r )，从而求出r 的分布列．3．超几何分布中，求概率时需要求组合数，同学们要熟练掌握组合数的性质及计算方法，以便简化计算．[对应学生用书P28][例1] 得1分，一个红球得2分，求某人摸出5个球，恰好得7分的概率．[思路点拨] 摸出5个球得7分，即摸出2个红球，3个白球，然后利用超几何分布的概率公式求解即可．[精解详析] 设摸出的红球个数为X ，则X 服从超几何分布，其中N ＝25，M ＝10，n ＝5，由于摸出5个球，得7分，仅有两个红球的可能，那么恰好得7分的概率为P (X ＝2)＝C 210C 315C 525≈0.385，即恰好得7分的概率约为0.385.[一点通] 解答此类问题的关键是先分析随机变量是否满足超几何分布．若满足，则直接利用公式解决；若不满足，则应借助相应概率公式求解．1．从一批含有13件正品、2件次品的产品中，不放回任取3件，求取得2件次品的概率．解：设随机变量X 表示取出次品的件数，则X 服从超几何分布，其中N ＝15，M ＝2，n ＝3.可能的取值为0,1,2，则P (X ＝3)＝C 22C 113C 315＝135.2．甲参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6道题，规定每次考试都从备选题中随机抽出3道题进行测试，至少答对2题才算及格．求甲及格的概率．解：设X 为甲答对题的数量，则X ＝0,1,2,3.则甲及格的概率为P (X ＝2)＋P (X ＝3)＝C 14C 26C 310＋C 04C 36C 310＝12＋16＝23.所选3人中女生的人数，求X 的概率分布及P (X <2)．[思路点拨] 可以将8人看作8件“产品”，3名女生看作3件“次品”，任选3人中女生的人数可看作是任取3件“产品”中所含的“次品”数．[精解详析] 由题意分析可知，随机变量X 服从超几何分布．其中N ＝8，M ＝3，n ＝3，所以P (X ＝0)＝C 35C 03C 38＝528，P (X ＝1)＝C 25C 13C 38＝1528，P (X ＝2)＝C 15C 23C 38＝1556，P (X ＝3)＝C 05C 33C 38＝156.从而随机变量X 的概率分布为X 0 1 2 3 P52815281556156所以P (X <2)＝P (X ＝0)＋P (X ＝1)＝528＋1528＝57.[一点通] 求超几何分布的概率分布，关键是明确随机变量确实服从超几何分布及随机变量的取值，分清M ，N ，n 的值，然后代入公式即可求出相应取值的概率，最后列表即可．3．2014年8月16日第二届青年奥林匹克运动会将在南京举行，当地某学校招募了8名男志愿者和12名女志愿者．将这20名志愿者的身高编成如下茎叶图(单位：cm)：若身高在180 cm 以上(包括180 cm)定义为“高个子”，身高在180 cm 以下(不包括180 cm)定义为“非高个子”，且只有“女高个子”才能担任“礼仪小姐”．(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5人中选2人，那么至少有一人是“高个子”的概率是多少？(2)若从所有“高个子”中选3名志愿者，用X 表示所选志愿者中能担任“礼仪小姐”的人数，试写出X 的概率分布．解：(1)根据茎叶图，有“高个子”8人，“非高个子”12人， 用分层抽样的方法，每个人被抽中的概率是520＝14，所以选中的“高个子”有8×14＝2人，“非高个子”有12×14＝3人．用事件A 表示“至少有一名‘高个子’被选中”， 则它的对立事件A 表示“没有一名‘高个子’被选中”， 则P (A )＝1－C 23C 25＝1－310＝710.因此，至少有一人是“高个子”的概率是710.(2)依题意，所选志愿者中能担任“礼仪小姐”的人数X 的取值分别为0,1,2,3.P (X ＝0)＝C 34C 38＝114，P (X ＝1)＝C 14C 24C 38＝37，P (X ＝2)＝C 24C 14C 38＝37，P (X ＝3)＝C 34C 38＝114.因此，X 的概率分布如下：X 0 1 2 3 P11437371144．某校高三年级某班的课外活动小组中有6名男生，4名女生，从中选出4人参加数学竞赛，用X 表示其中的男生人数，求X 的分布列．解：依题意随机变量X 服从超几何分布，所以P (X ＝r )＝C r 6C 4－r4C 410(r ＝0,1,2,3,4)．P (X ＝0)＝C 06C 44C 410＝1210，P (X ＝1)＝C 16C 34C 410＝435，P (X ＝2)＝C 26C 24C 410＝37，P (X ＝3)＝C 36C 14C 410＝821，P (X ＝4)＝C 46C 04C 410＝114.故X 的分布列为[例3] 3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用X 表示取出的3个小球上的最大数字．求：(1)取出的3个小球上的数字互不相同的概率；(2)随机变量X 的概率分布；(3)计算介于20分到40分之间的概率． [思路点拨] (1)可利用古典概型公式求解；(2)先确定X 的取值，然后求对应的概率，最后列表即可；(3)由题意知介于20分到40分的概率等于X ＝3与X ＝4的概率之和．[精解详析] (1)法一：“一次取出的3个小球上的数字互不相同”的事件记为A ，则P (A )＝C 35C 12C 12C 12C 310＝23.法二：“一次取出的3个小球上的数字互不相同”的事件记为A ，“一次取出的3个小球上有两个数字相同”的事件记为B ，则事件A 和事件B 是对立事件．因为P (B )＝C 15C 22C 18C 310＝13，所以P (A )＝1－P (B )＝1－13＝23.(2)由题意，X 所有可能的取值为2,3,4,5.P (X ＝2)＝C 22C 12＋C 12C 22C 310＝130； P (X ＝3)＝C 24C 12＋C 14C 22C 310＝215； P (X ＝4)＝C 26C 12＋C 16C 22C 310＝310； P (X ＝5)＝C 28C 12＋C 18C 22C 310＝815. 所以随机变量X 的概率分布为X 2 3 4 5 P130215310815(3)“一次取球得分介于20分到40分之间”的事件记为C ，则P (C )＝P (X ＝3)＋P (X ＝4)＝215＋310＝1330.[一点通] 本题将排列、组合、古典概型、分布列的知识融于一体，在知识上相互联系，解决此类问题的关键在于正确地处理好等可能事件的概率、对立事件的概率间的关系，并结合分布列的有关知识把相应的问题细化．5．老师要从10篇课文中随机抽3篇让学生背诵，规定至少要背出2篇才能及格．某同学只能背诵其中的6篇，试求：(1)抽到他能背诵的课文的数量的分布列；(2)他能及格的概率．解：(1)设随机抽取的3篇课文中该同学能背诵的篇数为X ，则X 服从超几何分布，它可能的取值为0,1,2,3.P (X ＝r )＝C r 6C 3－r 4C 310(r ＝0,1,2,3)．∴P (X ＝0)＝C 34C 310＝130，P (X ＝1)＝C 16C 24C 310＝310，P (X ＝2)＝C 26C 14C 310＝12，P (X ＝3)＝C 36C 310＝16，∴X 的分布表如下.(2)该同学能及格表示他能背出2篇或3篇课文，故他能及格的概率为 P (X ≥2)＝P (X ＝2)＋P (X ＝3)＝12＋16＝23.6．某高二数学兴趣小组有7位同学，其中有4位同学参加过高一数学“南方杯”竞赛．若从该小组中任选3位同学参加高二数学“南方杯”竞赛，求这3位同学中参加过高一数学“南方杯”竞赛的同学数X 的概率分布及P (X <2)．解：由题意可知，X 的可能取值为0,1,2,3.则P (X ＝0)＝C 04C 33C 37＝135，P (X ＝1)＝C 14C 23C 37＝1235，P (X ＝2)＝C 24C 13C 37＝1835，P (X ＝3)＝C 34C 03C 37＝435.所以随机变量X 的概率分布为P (X <2)＝P (X ＝0)＋P (X ＝1)＝135＋1235＝1335.1．超几何分布的判断判断随机变量是否服从超几何分布，可以从以下两个方面判断：一是超几何分布描述的是不放回抽样问题；二是随机变量为抽到的某类个体的个数．2．超几何分布的分布列的求法(1)在超几何分布中，只要知道N ，M 和n ，就可以根据公式，求出X 取不同r 值时的概率P (X ＝r )，从而列出X 的分布列．(2)一旦掌握了X 的分布列，就可以算出相应试验的很多事件的概率，从而就完全掌握了该试验．[对应课时跟踪训练(十一)]一、填空题1．盒中有4个白球，5个红球，从中任取3个球，则取出1个白球和2个红球的概率是________．解析：设随机变量X 为抽到白球的个数，X 服从超几何分布，由公式，得P (X ＝1)＝C 14C 25C 39＝4×1084＝1021.答案：10212．有10位同学，其中男生6位，女生4位，从中任选3人参加数学竞赛．用X 表示女生人数，则概率P (X ≤2)＝________.解析：P (X ≤2)＝P (X ＝1)＋P (X ＝2)＋P (X ＝0)＝C 14C 26C 310＋C 24C 16C 310＋C 36C 310＝2930. 答案：29303．若在甲袋内装有8个白球，4个红球，在乙袋内装有6个白球，6个红球，今从两袋内任意取出1个球，设取出的白球个数为X ，则P (X ＝1)＝________.解析：P (X ＝1)＝C 18C 16＋C 14C 16C 112C 112＝12. 答案：124．某12人的兴趣小组中，有5名“三好生”，现从中任意选6人参加竞赛，用X 表示这6人中“三好生”的人数，则当X 取________时，对应的概率为C 35C 37C 612.解析：由题意可知，X 服从超几何分布，由概率值中的C 35可以看出“从5名三好生中选取了3名”．答案：35．50张彩票中只有2张中奖票，今从中任取n 张，为了使这n 张彩票里至少有一张中奖的概率大于0.5，n 至少为________．解析：用X 表示中奖票数，P (X ≥1)＝C 12C n －148C n 50＋C 22C n －248C n 50>0.5.解得n ≥15. 答案：15 二、解答题6．从一副不含大小王的52张扑克牌中任意抽出5张，求至少有3张A 的概率． 解：设抽出的5张牌中所包含的A 牌的张数为X ，则X 服从超几何分布，其分布列为P (X ＝r )＝C r 4C 5－r48C 552，r ＝0,1,2,3,4.所以随机变量X 的概率分布为：所以抽出的5张牌中至少有3张A 的概率为P (X ≥3)＝P (X ＝3)＋P (X ＝4)＝C 34C 248C 552＋C 44C 148C 552≈0.001 75.7．在10件产品中，有3件一等品，4件二等品，3件三等品，从这10件产品中任取3件，求：(1)取出的3件产品中一等品件数X 的分布列；(2)取出的3件产品中一等品件数多于二等品件数的概率．解：(1)由于从10件产品中任取3件的结果数为C 310，从10件产品中任取3件，其中恰有r 件一等品的结果数为C r 3C 3－r7，那么从10件产品中任取3件，其中恰有r 件一等品的概率为P (X ＝r )＝C r 3C 3－r7C 310，r ＝0,1,2,3.所以随机变量X 的分布列是(2)设“取出的3“恰好取出1件一等品和2件三等品”为事件A 1，“恰好取出2件一等品”为事件A 2，“恰好取出3件一等品”为事件A 3.由于事件A 1，A 2，A 3彼此互斥，且A ＝A 1∪A 2∪A 3，而P (A 1)＝C 13C 23C 310＝340，P (A 2)＝P (X ＝2)＝740，P (A 3)＝P (X ＝3)＝1120，所以取出的3件产品中一等品件数多于二等品件数的概率为 P (A )＝P (A 1)＋P (A 2)＋P (A 3)＝340＋740＋1120＝31120.8．在一次购物抽奖活动中，假设10张奖券中有一等奖奖券1张，可获价值50元的奖品，有二等奖奖券3张，每张可获价值10元的奖品，其余6张没有奖品．(1)顾客甲从10张奖券中任意抽取1张，求中奖次数X 的概率分布． (2)顾客乙从10张奖券中任意抽取2张， ①求顾客乙中奖的概率；②设顾客乙获得的奖品总价值Y 元，求Y 的概率分布．解：(1)抽奖一次，只有中奖和不中奖两种情况，故X 的取值只有1和0两种情况． P (X ＝1)＝C 14C 110＝410＝25，则P (X ＝0)＝1－P (X ＝1)＝1－25＝35.因此X 的概率分布为X ＝k 0 1 P (X ＝k )3525(2)①顾客乙中奖可分为互斥的两类：所抽取的2张奖券中有1张中奖或2张都中奖．故所求概率P ＝C 14C 16＋C 24C 06C 210＝3045＝23. ②Y 的所有可能取值为0,10,20,50,60，且P (Y ＝0)＝C 04C 26C 210＝1545＝13，P (Y ＝10)＝C 13C 16C 210＝1845＝25，P (Y ＝20)＝C 23C 06C 210＝345＝115，P (Y ＝50)＝C 11C 16C 210＝645＝215，P (Y ＝60)＝C 11C 13C 210＝345＝115.因此随机变量Y 的概率分布为。

§2.2 超几何分布课时目标1.通过实例，理解超几何分布，能进行简单应用.2.进一步理解随机变量的概率分布的性质、意义．超几何分布：一般地，若一个随机变量X 的分布列为P (X ＝r )＝________________，其中r ＝0,1,2,3，…，l ，l ＝min(n ，M )，则称X 服从超几何分布，记为X ～H (n ，M ，N )，并将P (X ＝r )＝C r M C n －r N －M C n N，记为______．一、填空题1．下列随机事件中的随机变量X 服从超几何分布的是______．(填序号)①将一枚硬币连抛3次，正面向上的次数记为X ；②从7男3女共10个学生干部中选出5个优秀学生干部，女生的人数记为X ；③某射手的射击命中率为0.8，现对目标射击1次，记命中的次数为X ；④盒中有4个白球和3个黑球，每次从中摸出1个球且不放回，X 是第一次摸出黑球的次数．2．100个乒乓球中，有5个是不合格的，现从中抽取10个，用X 表示次品数，则P (X ＝2)＝________.(用式子表示)．3．从每组6人的4个小组中，任意地选取4人去开座谈会，用随机变量η表示选取出来的组长的人数，则恰好有3名组长被选出的概率记作为________．4．在15个村庄中，有7个村庄交通不太方便，现从中任意选10个村庄，用ξ表示10个村庄中交通不太方便的村庄数，P (ξ＝4)＝________.(用式子表示)5．一批产品共50件，其中5件次品，45件合格品，从这批产品中任意抽2件，则出现次品的概率为______．6．一个盒子里装有相同大小的黑球10个，红球12个，白球4个，从中任取两个，其中白球的个数记为ξ，则P(ξ≤1)＝________.7．从4名男生和2名女生中任选3人参加数学竞赛，则所选3人中，女生人数不超过1人的概率为______．8．为了庆祝六一儿童节，某食品厂制作了3种不同的精美卡片，每袋食品随机装入一张卡片，集齐3种卡片可获奖，现购买该种食品5袋，能获奖的概率为________．二、解答题9．50张彩票中只有2张中奖票，今从中任取n张，为了使这n张彩票里至少有一张中奖的概率大于0.5，则n至少为多少？10．某医院内科有5名主任医师和15名主治医师，现从中随机地挑选4人组织一个医疗小组．设X是4人中主任医师的人数．(1)写出X的分布列；(2)求4人中至少有1名主任医师的概率．(精确到0.001)能力提升11．盒中装有一打(12个)乒乓球，其中9个新的，3个旧的，从盒中任取3个来用，使用完后装回盒中，此时盒中旧球个数X是一个随机变量，求X的概率分布表．12．从5名男生和3名女生中任选3人参加奥运会火炬接力活动．若随机变量X表示所选3人中女生的人数，求X的分布表及P(X<2)．1．在超几何分布中，只要知道N ，m 和n ，就可以根据公式，求出P (X ＝r )，从而得到X 的分布列．2．对超几何分布中的字母要理解含义，公式不能死记．2．2 超几何分布答案知识梳理C r M C n －r N －MC n NH (r ；n ，M ，N ) 作业设计1．②2.C 25C 895C 101003．H (3；4,4,24)4.C 47C 68C 10155.47245解析 设抽到的次品数为X ，则X 服从超几何分布，其中，N ＝50，M ＝5，n ＝2.于是出现次品的概率为P (X ≥1)＝P (X ＝1)＋P (X ＝2)＝C 15C 2－150－5C 250＋C 25C 2－250－5C 250＝949＋2245＝47245. 6.319325解析 ∵P (ξ＝0)＝C 222C 226，P (ξ＝1)＝C 122C 14C 226， ∴P (ξ≤1)＝P (ξ＝0)＋P (ξ＝1)＝C 222＋C 122C 14C 226＝319325. 7．0.8解析 设所选女生数为随机变量X ，X 服从超几何分布，P (X ≤1)＝P (X ＝0)＋P (X ＝1)＝C 02C 34C 36＋C 12C 24C 36＝45＝0.8. 8.5081解析 能获奖有以下两种情况：①5袋食品中三种卡片数分别为1,1,3，此时共有C 15C 14A 22×A 33＝60(种)不同的方法，其概率为P 1＝6035＝2081；②5袋食品中三种卡片数分别为2,2,1，共有C 25C 23A 22×A 33＝90(种)不同的装法，其概率为P 2＝9035＝3081，所以所求概率P ＝P 1＋P 2＝5081. 9．解 设随机变量X 表示“抽出中奖票的张数”，则X 服从超几何分布H (n,2,50)，根据公式可得至少有一张中奖的概率P (X ≥1)＝C 12C n －148C n 50＋C 22C n －248C n 50>0.5，解得n ≥15. 答 n 至少为15.10．解 (1)由题意可得，随机变量X 服从超几何分布H (4,5,20)，所以X 的分布列为P (X ＝r )＝C r 5C 4－r 15C 420，r ＝0,1,2,3,4. (2)P (X ≥1)＝1－P (X <1)＝1－P (X ＝0)＝1－C 05C 415C 420＝1－91323≈0.718. 答 4人中至少有1名主任医师的概率为0.718.11．解 设所取的3个球中有Y 个旧球，则Y 属于超几何分布，Y 可取0,1,2,3，P (Y ＝0)＝C 39C 312＝2155，P (Y ＝1)＝C 13·C 29C 312＝2755， P (Y ＝2)＝C 23·C 19C 312＝27220，P (Y ＝3)＝C 33C 312＝1220. 又X ＝3＋(3－Y )＝6－Y ，X 可取3,4,5,6，故P (X ＝3)＝P (Y ＝3)，P (X ＝4)＝P (Y ＝2)，P (X ＝5)＝P (Y ＝1)，P (X ＝6)＝P (Y ＝0)．X 的概率分布表为12．解 N ＝8，M ＝3，n ＝3，所以P (X ＝0)＝C 35C 03C 38＝528；P (X ＝1)＝C 25C 13C 38＝1528；P (X ＝2)＝C 15C 23C 38＝1556； P (X ＝3)＝C 05C 33C 38＝156. 从而随机变量X所以P (X <2)＝P (X ＝＝528＋1528＝57.。

《超几何分布》一节课的教学设计三维目标:1. 知识与技能:⑴通过实例，理解超几何分布及其特点⑵掌握超几何分布列及其导出过程⑶通过对实例的分析，会进行简单的应用2.. 过程与方法：启发引导学生分析实例-总结规律-练习巩固3. 情感、态度、价值观：⑴渗透联系的观点；⑵培养学生学习数学的兴趣教学重点1. 超几何分布及其推导过程及其特点2. 利用超几何分布来解决实际问题教学难点对超几何分布的理解及应用教学方法研究讨论；启发引导；讲练结合学法指导1.结合实例理解超几何分布列及其导出过程2.通过练习进行巩固和提高教学过程设计一、复习引入：1、随机变量：如果随机试验的结果可以用一个变量来表示，那么这样的变量叫做随机变量随机变量常用希腊字母ξ、η等表示2. 离散型随机变量: 随机变量只能取有限个数值或可列无穷多个数值则称为离散随机变量，在高中阶段我们只研究随机变量取有限个数值的情形.3. 分布列:设离散型随机变量ξ可能取得值为x 1，x 2，…，x 3，…，ξ取每一个值x i （i=1，2，…）的概率为()i i P x p ξ==，则称表为随机变量ξ的概率分布，简称ξ的分布列4. 分布列的两个性质：任何随机事件发生的概率都满足:1)(0≤≤A P ，并且不可能事件的概率为0，必然事件的概率为1．由此你可以得出离散型随机变量的分布列都具有下面两个性质：⑴P i ≥0，i ＝1，2，…；⑵P 1+P 2+ (1)对于离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率的和 即⋅⋅⋅+=+==≥+)()()(1k k k x P x P x P ξξξ二．问题探究：超几何分布：在产品质量的不放回抽检中，若件产品中有件次品，抽检件时所得次品数X=m则()m M m n N n M NC C P X m C --==.此时我们称随机变量X 服从超几何分布 1）超几何分布的模型是不放回抽样2）超几何分布中的参数是M,N,n三、数学应用例1．在一个口袋中装有30个球，其中有10个红球，其余为白球，这些球除颜色外完全相同.游戏者一次从中摸出5个球.摸到4个红球就中一等奖，那么获一等奖的概率是多少？解：由题意可见此问题归结为超几何分布模型.其中N = 30. M = 10. n = 5.P （一等奖）= P(X=4） + P(X=5）X 由公式P(X=k)=k n k M N MnN C C C k=0,1,2,...得：P(X=4）=411020530C C C ；P(X=5）= 501020530C C CP （一等奖） =0.0312答： 获一等奖的概率是0.0312 。