随机信号分析基础第五章习题王永德答案

1第一次作业：练习一之1、2、3题1.1 离散随机变量X 由0，1，2，3四个样本组成，相当于四元通信中的四个电平，四个样本的取值概率顺序为1/2，1/4，1/8，和1/8。

求随机变量的数学期望和方差。

解：875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=i i i x X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F求（1）系数A ；（2）X 取值在（0.5，1）内的概率)15.0(<<x P 。

解：⎪⎩⎪⎨⎧<≤-π==其他0201)](2π[cos 2)()(x x A dx x dF x f 由1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P1.3 试确定下列各式是否为连续随机变量的概率分布函数，如果是概率分布函数，求其概率密度。

（1）⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x （2）⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x x x x F （3）0)]()([)(>--=a a x u x u a xx F （4）0)()()(>---=a a x u axa x u a x x F2解：（1）⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x 当0≥x 时，对于12x x ≥，有)()(12x F x F ≥，)(x F 是单调非减函数； 1)(0≤≤x F 成立；)()(x F x F =+也成立。

第五章 习题5-1 设某信号为1000||()t x t e -=（1）试求x (t )的傅里叶变换X (j ω)，并绘制X (j ω)曲线；（2）假设分别以采样频率为f s =5000Hz 和f s =1000Hz 对该信号进行采样，得到一组采样序列x k ，说明采样频率对序列x k 频率特性X (e j Ω)的影响。

解：（1）1000||622000()()10j t t j t X j x t e dt e e dt ωωωω∞∞----∞-∞===+⎰⎰. X (j ω)的曲线如下图所示：（2）设采样周期为T ，则采样输出为()()()()k k k x x t t kT x kT t kT δδ∞∞=-∞=-∞=-=-∑∑.由时域相乘等于频域卷积，有1122()()*[()]()*[()]22j k k X e X j t kT X j kT Tππδδππ∞∞Ω=-∞=-∞=Ω-=ΩΩ-∑∑F 121212()()()2k k X j k d X j jk T T T T Tπππωδωωπ∞∞∞-∞=-∞=-∞=⋅=Ω--=Ω-∑∑⎰. 即序列x k 频率特性X (e j Ω)是原信号频谱X (j ω)以2Tπ为周期进行延拓而成的，而采样频率1122s f T Tππ==⋅，所以采样频率越高，序列x k 频率特性的各周期越分散，越不容易发生频谱混叠。

5-2 假设平稳随机过程x (t )和y (t )满足下列离散差分方程11;k k k k k k k x ax e y ay x v ---=-=+式中，|a|<1；e k ，v k ～N (0，σ 2)分布，且二者互不相关。

试求随机序列y k 的功率谱。

解：对1k k k x ax e --=进行离散时间傅里叶变换（DTFT ），且记DTFT(x k )=X (e j Ω)，DTFT(e k )=E (e j Ω)，则有j j j ()(1)()X e ae E e ΩΩΩ--=式中，Ω=ωT s ，称为数字频率（rad ），ω为实际频率（rad/s ），T s 为采样周期（s ）。

第5章习题参考答案1．请在括号内填入适当答案。

在CPU中：(1)保存当前正在执行的指令的寄存器是（IR ）；(2)保存当前正在执行的指令地址的寄存器是（AR ）(3)算术逻辑运算结果通常放在（DR ）和（通用寄存器）。

2．参见图5.15的数据通路。

画出存数指令“STO Rl，(R2)”的指令周期流程图，其含义是将寄存器Rl的内容传送至(R2)为地址的主存单元中。

标出各微操作信号序列。

解：STO R1, (R2)的指令流程图及为操作信号序列如下：STO R1, (R2)R/W=RDR O, G, IR iR2O, G, AR iR1O, G, DR iR/W=W3．参见图5.15的数据通路，画出取数指令“LAD (R3)，R0”的指令周期流程图，其含义是将(R3)为地址主存单元的内容取至寄存器R2中，标出各微操作控制信号序列。

解：LAD R3, (R0)的指令流程图及为操作信号序列如下：PC O , G, AR i R/W=R DR O , G, IR iR 3O , G, AR i DR O , G, R 0iR/W=R LAD (R3), R04．假设主脉冲源频率为10MHz ，要求产生5个等间隔的节拍脉冲，试画出时序产生器的逻辑图。

解：5．如果在一个CPU 周期中要产生3个节拍脉冲；T l ＝200ns ，T 2=400ns ，T 3=200ns ，试画出时序产生器逻辑图。

解：取节拍脉冲T l 、T 2、T 3的宽度为时钟周期或者是时钟周期的倍数即可。

所以取时钟源提供的时钟周期为200ns ，即，其频率为5MHz.；由于要输出3个节拍脉冲信号，而T 3的宽度为2个时钟周期，也就是一个节拍电位的时间是4个时钟周期，所以除了C 4外，还需要3个触发器——C l 、C 2、C 3；并令211C C T *=；321C C T *=；313C C T =，由此可画出逻辑电路图如下：6．假设某机器有80条指令，平均每条指令由4条微指令组成，其中有一条取指微指令是所有指令公用的。

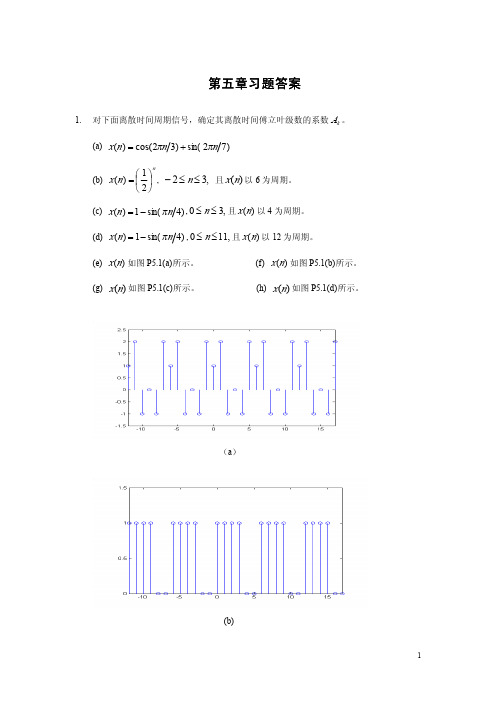
5.1 求题图5.1中三个电路的传输函数（不考虑输出负载）。

RRC1C 2C 1C 2C 1R 2R题图5.1解根据电路分析、信号与系统的知识， 第一个图中系统的传输函数 1/1()1/1j C H j R j C j RCωωωω==++ 第二个图中系统地传输函数 ()21112211/1()/11/1/j C j RC H j R j C j R C C j C R j C ωωωωωωω+==++++ 第三个图中系统地传输函数()2222212111221212121122/1/()//1/1/R j C R j C R j R R C H j R j C R j C R R j R R C C R j C R j C ωωωωωωωωω++==++++++5.2若平稳随机信号)(t X 的自相关函数||2)(ττ-+=BeA R X ，其中，A 和B 都是正常数。

又若某系统冲击响应为()()wth t u t te -=。

当)(t X 输入时，求该系统输出的均值。

解： 因为[]()22X EX R A =∞=所以[]E X A A =±=±。

()()()()()20wt A E Y t E h X t d E X t h d A te dt wξξξξξ∞∞∞--∞-∞±⎡⎤=-==±=⎡⎤⎡⎤⎣⎦⎣⎦⎢⎥⎣⎦⎰⎰⎰ 5.35.4 若输入信号00()cos()X t X t ω=++Φ作用于正文图5.2所示RC 电路，其中0X 为[0,1]上均匀分布的随机变量，Φ为[0,2π]上均匀分布的随机变量，并且0X 与Φ彼此独立。

求输出信号Y(t)的功率谱与相关函数。

解：首先我们求系统的频率响应()H j ω。

根据电路分析、信号与系统的知识，/1/11()()()1/1t RCj C H j h t e u t R j C j RCRCωωωω-==↔=++ 然后，计算)(t X 的均值与自相关函数，[]()1/2X m E X t ==[]{}(){}{}0000(,)cos cos X R t t EXt X t τωωτ+=++Φ+++Φ=⎡⎤⎣⎦()01/31/2cos ωτ+可见)(t X 是广义平稳的。

随机信号分析习题一1. 设函数⎩⎨⎧≤>-=-0 ,0 ,1)(x x e x F x ，试证明)(x F 是某个随机变量ξ的分布函数.并求下列概率：)1(<ξP ，)21(≤≤ξP 。

2. 设),(Y X 的联合密度函数为(), 0, 0(,)0 , otherx y XY e x y f x y -+⎧≥≥=⎨⎩, 求{}10,10<<<<Y X P 。

3. 设二维随机变量),(Y X 的联合密度函数为⎥⎦⎤⎢⎣⎡++-=)52(21exp 1),(22y xy x y x f XY π 求:（1）边沿密度)(x f X ,)(y f Y（2)条件概率密度|(|)Y X f y x ，|(|)X Y f x y4. 设离散型随机变量X 的可能取值为{}2,1,0,1-，取每个值的概率都为4/1，又设随机变量3()Y g X X X ==-。

(1）求Y 的可能取值 （2）确定Y 的分布. （3）求][Y E 。

5. 设两个离散随机变量X ，Y 的联合概率密度为:)()(31)1()3(31)1()2(31),(A y A x y x y x y x f XY --+--+--=δδδδδδ试求：（1)X 与Y 不相关时的所有A 值。

（2）X 与Y 统计独立时所有A 值。

6. 二维随机变量（X ，Y )满足:ϕϕsin cos ==Y Xϕ为在[0，2π]上均匀分布的随机变量，讨论X ,Y 的独立性与相关性。

7. 已知随机变量X 的概率密度为)(x f ,求2bX Y =的概率密度)(y f .8. 两个随机变量1X ，2X ,已知其联合概率密度为12(,)f x x ,求12X X +的概率密度？9. 设X 是零均值，单位方差的高斯随机变量，()y g x =如图，求()y g x =的概率密度()Y f y\10. 设随机变量W 和Z 是另两个随机变量X 和Y 的函数222W X Y Z X⎧=+⎨=⎩ 设X ，Y 是相互独立的高斯变量。

1第一次作业：练习一之1、2、3题1.1 离散随机变量X 由0，1，2，3四个样本组成，相当于四元通信中的四个电平，四个样本的取值概率顺序为1/2，1/4，1/8，和1/8。

求随机变量的数学期望和方差。

解：875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=ii ix X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F 求（1）系数A ；（2）X 取值在（0.5，1）内的概率)15.0(<<x P 。

解：⎪⎩⎪⎨⎧<≤-π==其他201)](2π[cos 2)()(x x A dx x dF x f由 1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P 1.3 试确定下列各式是否为连续随机变量的概率分布函数，如果是概率分布函数，求其概率密度。

（1）⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x2（2）⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x xx x F （3）0)]()([)(>--=a a x u x u ax x F （4）0)()()(>---=a a x u ax a x u a x x F解：（1）⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x当0≥x 时，对于12x x ≥，有)()(12x F x F ≥，)(x F 是单调非减函数；1)(0≤≤x F 成立； )()(x F x F =+也成立。