(完整版)组合体练习题
- 格式:ppt
- 大小:5.97 MB
- 文档页数:66

组合体三视图练习题课程学习目标[课程目标]目标重点:正投影与三视图的画法与应用, 目标难点:三视图的画法以及应用学法关键1.画三视图时,可以把垂直投影面的视线想象成平行光线从不同的方向射向几何体,体会可见的轮廓线的投影就是所要画出的视图,画出的三视图要检验是否符合.长对正、高平齐、宽相等.的基本特征.2.由三视图想象几何体时也要根据.长对正、高平齐、宽相等.的基本特征,想象视图中每部分对应的实物的形象,特别注意几何体中与投影面垂直或平行的线及面的位置研习教材重难点研习点1 正投影1.定义:在物体的平行投影中,如果投射线与投射面垂直,则称这样的平行投影为正投影.. 正投影的性质:①直线或线段的平行投影仍是直线或线段;②平行直线的平行投影是平行或重合的直线;③平行于投影面的线段,它的投影与这条线段平行且等长;④与投影面平行的平面图形,它的投影与这个图形全等;⑤在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比;⑥垂直于投影面的直线或线段的正投影是点;⑦垂直于投影面的平面图形的正投影是直线或直线的一部分.研习点三视图1. 水平投射面:一个投射面水平放置,叫做水平投射面.. 俯视图:投射到水平投射面内的图形叫做俯视图.3. 直立投射面:一个投射面放置在正前方,这个投射面叫做直立投射面.. 主视图:投射到直立投射面内的图形叫做主视图.5. 侧立投射面:和直立、水平两个投射面都垂直的投射面叫做侧立投射面.. 左视图:投射到侧立投射面内的图形叫做左视图.7. 三视图:将空间图形向水平投射面、直立投射面、侧立投射面作正投影,然后把这三个投影按一定的布局放在一个平面内,这样构成的图形叫做空间图形的三视图.研习点3.三视图的画法要求:三视图的主视图、俯视图、左视图分别是人从物体的正前方、正上方、正左方看到的物体轮廓线的正投影组成的平面图形;一个物体的三视图的排列规则是:俯视图放在主视图的下面,长度与主视图一样,左视图放在主视图的右面,高度与主视图一样,宽度与俯视图的宽度一样;记忆口诀:长对正,高平齐,宽相等;主左一样高,主俯一样长,俯、左一样宽。

大学组合体试题及答案一、单项选择题(每题2分,共20分)1. 组合体的体积等于其各个组成部分体积之和,这是基于什么原理?A. 体积守恒原理B. 体积不变原理C. 体积相加原理D. 体积叠加原理答案:C2. 在组合体中,两个物体的接触面被称为什么?A. 界面B. 接触面C. 表面D. 边界答案:B3. 组合体的表面积计算时,需要考虑哪些因素?A. 各个组成部分的表面积B. 各个组成部分的体积C. 各个组成部分的质量D. 各个组成部分的密度答案:A4. 组合体的重心位置取决于什么?A. 各个组成部分的质量B. 各个组成部分的体积C. 各个组成部分的形状D. 所有上述因素答案:D5. 组合体的稳定性主要受哪些因素影响?A. 重心位置B. 接触面积C. 外部力的作用D. 所有上述因素答案:D二、填空题(每题2分,共20分)1. 当两个物体完全重合时,它们的组合体的体积等于_______。
答案:单个物体的体积2. 组合体的表面积计算时,需要减去_______的面积。
答案:接触面3. 组合体的重心位置可以通过_______的方法来确定。
答案:质量分布4. 如果组合体中的一个物体发生位移,那么组合体的_______也会随之改变。
答案:重心位置5. 组合体的稳定性可以通过增加_______来提高。
答案:接触面积三、简答题(每题10分,共30分)1. 描述组合体的体积计算公式,并举例说明。
答案:组合体的体积计算公式为V = V1 + V2 + ... + Vn,其中V是组合体的总体积,V1、V2、...、Vn是各个组成部分的体积。
例如,如果有一个立方体和一个球体组合在一起,它们的体积分别为V1和V2,那么组合体的体积就是V = V1 + V2。
2. 解释为什么组合体的稳定性与重心位置有关。
答案:组合体的稳定性与重心位置有关,因为重心是物体重力作用的平衡点。
如果重心位置较低,物体就更稳定,因为需要更大的力才能使其倾斜或翻倒。

《机械制图》第五章组合体试卷一、单项选择题1.当完整标注了圆锥的尺寸后,只要用( )个视图就能确定其形状及大小。
(2 分)A.1个B.2个C.3个D.4个2.组合体的各形体的相邻表面之间可能形成( )特殊关系。
(2 分)A.共面和不共面B.共面、相切和相交三种C.共面和相交两种D.共面、不共面、相切和相交四种3.视图中的一个圆形线框,可能是( )。
(2 分)A.圆柱或圆柱孔的投影B.圆锥或圆锥槽的投影。
C.圆球、半球或半圆槽的投影D.多种可能4.组合体上有5个相同直径为8㎜的圆孔,应在某一孔的投影图上标注为( )。
(2 分)A.5-8B.5-ф8C.5×8D.5×ф85.视图中的一个矩形线框,可能是( )。
(2 分)A.长方体的投影B.柱体的投影C.某一面的投影D.不仅是上述中的某一种6.圆柱应标注出( )。
(2 分)A.轴向尺寸和圆柱直径B.高度尺寸和圆柱直径C.长度尺寸和圆柱直径D.宽度尺寸和圆柱直径7.视图上的每个封闭线框,通常表示物体上一个( )的投影。
(2 分)A.平面B.平面和圆柱面C.平面或曲面D.曲面8.当两形体邻接表面共面时,在共面处( )邻接表面的分界线。
(2 分)A.没有B.有C.应有D.不一定9.当两形体邻接表面相切时,在平行于切线的投影面上切线的投影( )。
(2 分)A.应画出B.不画C.可不画D.一定画10.当完整标注了圆柱尺寸后,只要用( )个视图就能确定其形状及大小。
(2 分)A.1个B.2个C.3个D.4个二、判断题11.( )当两形体邻接表面相切时,切线的投影应画出。
(2 分)12.( )组合体上6个相同的圆孔ф8,要注明数量如6-ф8。
(2 分)13.( )当两圆柱实体相交时已融为一体,圆柱面上原来的一段转向轮廓线已不存在。
(2 分)14.( )实形体与空形体相邻表面相交,只要形体的大小和相对位置一致,其交线完全相同。
(2 分)15.( )画组合体时应先从反映形体特征轮廓且有积聚性投影的视图入手。

组合体视图单元测试(二)(试卷总分100分,考试时间90分钟)一、填空题:(20×1′)1、组合体的分析方法主要有法和法。
常用的是法。
2、选择组合体视图时,要求主视图能较多地表达物体的和。
3、叠加类组合体的形体表面接触方式有、和三种。
4、当截平面与圆柱轴线平行时,其截交线形状为,当截平面与圆柱垂直时,其截交线形状为,当截平面与圆柱轴线倾斜时,其截交线形状为。
5、尺寸基准按其几何形式可分为基准、基准和基准三种。
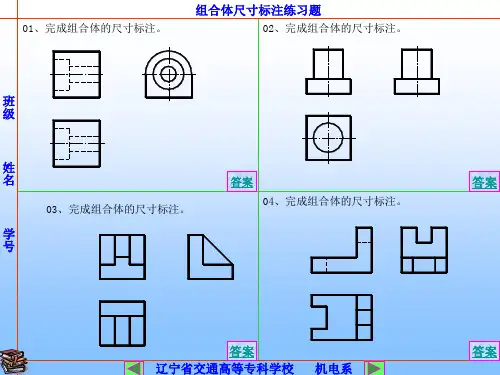
6、如下图,P是面EF是线Q是面S是面AB是线CD是线(第6题图)二、选择题:(10×2′)1、线面分析法主要适用于。
A、叠加类组合体B、切割类组合体C、综合类组合体2、下列关于基准的说法错误的是。
A、物体的长、宽、高方向都有基准B、基准是标注尺寸的起点C、必须用可以触摸到的实体作为基准3、主视图的选择原则是。
A、应选择最容易画的视图作主视图B、应选择表面线条最少的视图作主视图C、应选择最能表达物体形状特征的视图作主视图4、下列关于相贯线说法错误的是。
A、相贯线是两个形体的共有线B、相贯线一般情况下是闭合的空间曲线,有时则为平面曲线C、相贯线是对称的空间曲线5、下列关于截交线说法错误的是。
A、截交线一定是闭合的空间曲线B、截交线是截平面和几何体表面的共有线C、可以用辅助线法和辅助平面法求截交线6、用平行于圆锥表面素线的截平面截圆锥所得的截交线形状为。
A、双曲线B、抛物线C、过锥顶的两相交直线7、按给定的主、俯视图,找出相对应的左视。
A、B、C、8、按给定的主、俯视图,找出相对应的左视。
A、B、C、9、按给定的主、俯视图,找出相对应的左视。
A、B、C、D、10、按给定的主、俯视图,找出相对应的左视。
A、B、C、D、三、判断题:(10×1′)(正确的打“√”,错误的打“×”)1、组合体的尺寸包括定形尺寸、定位尺寸和总体尺寸三种。
()2、当截平面与圆球轴线成45度时,所得截交线为椭圆。

立体几何中的组合体问题专题(有答案)例1.正方体与球问题:正方体的棱长为1.求球的半径:⑴若正方体的八个顶点都在球面上,⑵若球内切于正方体;⑶12条棱组成一个正方体,一充气球在正方体内,求球的最大半径.例2.正四面体与球问题:正四面体的棱长为1.求球的半径:⑴若正四面体的四个顶点都在球面上,⑵若球内切于正四面体;⑶6条棱组成一个正四面体,一充气球在正四面体内,求球的最大半径.例3.四球问题:四个球的半径都为1.⑴桌面放两两相切的3个球,这3个球上面放一个球,求这个球的最高点离桌面的距离;⑵求与上述4个球都相切的小球的半径.例4.圆锥、圆柱与球⑴底面半径为1cm高为10cm的圆柱内,可以放几个半径为0.5cm的小球?⑵圆锥底面半径为3,高为4,一个球内切于圆锥,求球的半径;⑶圆锥底面半径为3,高为4,两个半径相同的球两两相切,放在圆锥底面上,且内切于圆锥,求这两个球的半径;⑷圆锥底面半径为3,高为4,三个半径相同的球两两相切,放在圆锥底面上,且内切于圆锥,求这两个球的半径;⑸圆锥底面半径为3,内接于一个半径为4的球,求圆锥的高.例5.圆锥与正四棱柱⑴圆锥底面半径为3,高为4,正四棱柱的高为3,且内接于圆锥,求正四棱柱的底面边长;⑵圆锥底面半径为3,高为4,正四棱柱的高为x,且内接于圆锥,求正四棱柱的体积.练习一、补(补成长方体或正方体)1. 一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为A 、3πB 、4πC 、33πD 、6π2. 在正三棱锥ABC S -中,M 、N 分别是棱SC 、BC 的中点,且AM MN ⊥,若侧棱32=SA ,则正三棱锥ABC S -外接球的表面积是( ) A .π12 B .π32 C .π36 D .π483. 点P 在直径为6的球面上,过P 作两两互相垂直的三条弦(两端点均在球面上的线段),若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是 A .6B .435C .2215D .210554. 一个正方体的体积是8,则这个正方体的内切球的表面积是( )A .8πB .6πC .4πD .π 5. 设正方体的棱长为233,则它的外接球的表面积为( )A .π38B .2πC .4πD .π346. 已知三棱锥S ABC -的三条侧棱两两垂直,且2,4SA SB SC ===,则该三棱锥的外接球的半径为 A .3 B .6 C .36 D .97. 已知长方体1111ABCD A B C D -的外接球的表面积为16,则该长方体的表面积的最大值为A .32B .36C .48D .648. 长方体1111ABCD A B C D -的各个顶点都在表面积为16π的球O 的球面上,其中1::2:1:3AB AD AA =,则四棱锥O ABCD -的体积为A .263 B . 63C .23D .3 9.【山东省潍坊一中2013届高三12月月考测试数学文】四棱锥P ABCD 的三视图如右图所示,四棱锥P ABCD 的五个顶点都在一个球面上,E 、F 分别是棱AB 、CD 的中点,直线EF 被球面所截得的线段长为22,则该球表面积为A .12B .24C .36D .4810. (河南省豫东、豫北十所名校2013届高三阶段性测试四)已知四面体ABCD 中,AB =AD =6,AC =4,CD =213,AB 丄平面ACD ,则四面体 ABCD 外接球的表面积为A . π36B . π88C . π92D . π12811. 正方体1111ABCD A B C D -的棱长为6,一个球与正方体的棱长都相切,则这个球的半径是____________.12. 三棱锥A -BCD 中,侧棱AB 、AC 、AD 两两垂直,ΔABC ,ΔACD , ΔADB 的面积分别为,222,则三棱锥A -BCD 的外接球的体积为. ______13. 四面体ABCD 中,共顶点A 的三条棱两两相互垂直,且其长分别为361、、,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。

组合体三视图练习题一、选择题(每题2分,共20分)1. 组合体三视图包括主视图、左视图和哪个视图?A. 俯视图B. 仰视图C. 侧视图D. 底视图2. 在组合体三视图中,主视图通常表示物体的哪个面?A. 正面B. 侧面C. 顶面D. 底面3. 以下哪个不是三视图的画法规则?A. 长对正B. 高平齐C. 宽相等D. 角度一致4. 组合体三视图中,如果一个视图上的线条与另一个视图上的线条不相交,这些线条表示的是?A. 同一条线B. 不同的线C. 相互平行的线D. 相互垂直的线5. 在组合体三视图中,如果一个物体的俯视图和左视图的尺寸相同,那么这个物体可能是?A. 立方体B. 圆柱体C. 圆锥体D. 球体6. 组合体三视图中,若主视图和俯视图的尺寸不同,但左视图与主视图尺寸相同,该物体可能是?A. 长方体B. 正方体C. 圆柱体D. 圆锥体7. 在组合体三视图中,若主视图和左视图的尺寸相同,但俯视图的尺寸不同,该物体可能是?A. 长方体B. 正方体C. 圆柱体D. 圆锥体8. 组合体三视图中,若主视图和左视图的尺寸不同,但俯视图与主视图尺寸相同,该物体可能是?A. 长方体B. 正方体C. 圆柱体D. 圆锥体9. 在组合体三视图中,若俯视图和左视图的尺寸相同,但主视图的尺寸不同,该物体可能是?A. 长方体B. 正方体C. 圆柱体D. 圆锥体10. 组合体三视图中,若俯视图是一个圆形,左视图和主视图是两个相同的矩形,该物体可能是?A. 长方体B. 圆柱体C. 圆锥体D. 球体二、填空题(每题2分,共20分)11. 组合体三视图中,______视图通常用来表示物体的顶面或底面。
12. 在组合体三视图中,______视图通常用来表示物体的侧面。
13. 组合体三视图中,______视图通常用来表示物体的正面。
14. 组合体三视图的画法规则包括______、______和______。
15. 如果一个物体的三视图都是圆形,那么这个物体可能是______。
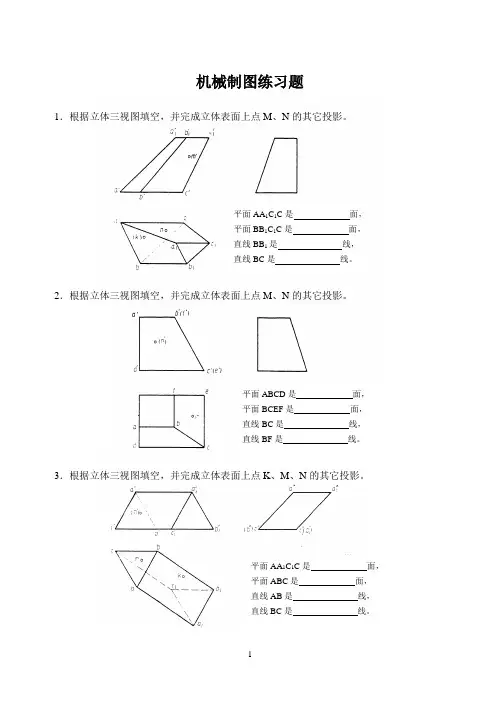
机械制图练习题1.根据立体三视图填空,并完成立体表面上点M 、N 的其它投影。
2.根据立体三视图填空,并完成立体表面上点M 、N 的其它投影。
3.根据立体三视图填空,并完成立体表面上点K 、M 、N 的其它投影。
平面ABCD 是 面, 平面BCEF 是 面, 直线BC 是 线, 直线BF 是 线。
平面AA 1C 1C 是 面, 平面BB 1C 1C 是 面, 直线BB 1是 线, 直线BC 是线。
4.根据立体三视图填空,并完成立体表面上点M 、N 的其它投影。
5.补画左视图漏线,并根据立体投影完成填空。
6.补画左视图漏线,并根据立体投影完成填空。
8.作出截切立体的水平投影和侧面投影9.作出截切立体的水平投影和侧面投影11.作出截切立体的水平投影12.补画立体的水平投影15.补画立体的水平投影18.完成立体相贯的正面投影和侧面投影20.完成立体相贯的正面投影23.完成侧面投影25.完成侧面投影26.完成侧面投影28.完成水平投影29.完成侧面投影32.完成侧面投影34.完成侧面投影35.完成侧面投影38.完成侧面投影39.完成侧面投影40.完成侧面投影41.完成正面投影42.完成侧面投影43.完成侧面投影44.完成正面投影46.完成全剖左视图47.完成全剖左视图49.完成全剖左视图50.完成全剖俯视图53.完成全剖左视图55.完成全剖左视图56.纠正螺纹的绘制错误,将正确的绘制在下面的指定位置57.纠正螺纹的绘制错误,将正确的绘制在下面的指定位置58.纠正螺纹旋合的绘制错误,将正确的绘制在下面的指定位置59.纠正螺纹旋合的绘制错误,将正确的绘制在下面的指定位置60.完成下列螺纹标注61.完成下列螺纹标注62.填空1、普通螺纹,大径24毫米,螺距3毫米,左旋,公差代号为7h 。
2、普通螺纹,大径20毫米,螺距2毫米,右旋,公差代号为7H 。
1、梯形螺纹,大径24毫米,导程10毫米,螺距5毫米,双线左旋,公差代号为7e 。