从勾股定理到图形面积关系的拓展定稿版

阅读材料从勾股定理到图形面积关系的拓展课题：直角三角形中的折叠问题教学目标：1.让学生理解折叠问题中的全等三角形及相等的线段和相等的角；2.让学生会灵活应用勾股定理构造方程解决简单的几何问题，感受面积法有时是解决几何问题的捷径；教学重点：掌握解决折叠问题的一般方法，体会方程思想的重要性.教学难点：折叠问题是操作问题，让学生会熟练寻找折叠前后图形中的相等量，并能顺利解决问题. 教学准备：每人一张直角三角形纸片.教学过程:一．新课导入：我们给定的三角形纸片命名为Rt△ABC，∠ACB=90°，AC=6，BC=8，则斜边AB= .二．新课教学：探究一：折叠中点与点的重合问题1：折叠△ABC使点B与点C重合，求折痕DE的长；【解析】由C、B两点关于DE轴对称，则DE垂直平分BC，所以DE是△ABC的中位线，DE=1AC=32问题2：折叠△ABC使点A与点C重合，求折痕FG的长；【解析】与问题同理可得FG=1BC=42问题3：折叠△ABC 使点A 与点B 重合，求折痕HI 的长.【解析】由HI 垂直平分AB 得AI=BI设AI=BI=x ，则CI=8-x∴2226(8)x x -=- ∴254x = 1122ABI S AB IH BI AC ∆=⋅=⋅即251068IH =⨯ ∴IH=258小结：1.利用全等三角形寻找相等的线段2.利用勾股定理及面积法求线段的长探究二：折叠中边与边的重叠问题1：折叠△ABC ，使AC 边落在AB 上的AC'处，求折痕AP 的长；【解析】由△ACP ≌AC ′P 得AC=AC ′，PC=PC ′=6，BC ′=4设PC=PC ′=x ，则BP=8-x2224(8)x x +=-∴x=3∴AP=226335+=问题2：折叠△ABC ，使BC 边落在BA 上的BC'处，求折痕BM 的长；【解析】与问题1同理，设CM=CM ′=x 可得83x =，则BM=1633 小结：一般用未重叠的直角三角形构造勾股定理.问题3：折叠△ABC ，使CA 边落在CB 上的CA'处，求折痕CN 的长.【解析】作ND ⊥BC 与点D∵∠CAN=∠BCN=45°，CA=CA ′=6，A ′B=2设CD=DN=x'2A BN ABC ACN S S S ∆∆∆=- ∴11126826222x x ⨯=⨯⨯-⨯⨯ ∴247x = ∴CN=2427 小结：面积法是捷径学以致用：如图所示，在矩形ACBD 中，AC=6，BC=8，沿对角线AB 折叠， △ABC 成为三角形ABE ，BE 交AD 于点F ，求EF 的长.【解析】由全等可得∠ABC=∠ABED∵AD ∥BC 得∠ABC=∠BAD∴∠ABE=∠BAD∴设AF=BF=x ，则EF=8-x∴2226(8)x x +-= ∴254x =即EF=254再探：若再沿GH 折叠，使点A 与点D 重合，求折痕GH 的长.【解析】∠BAE=∠ABDGH ∥BD 得∠AHG=∠ABD∴∠GAH=∠GHA∴AG=HG设PG=x ，则AG=HG=3+x∴2224(3)x x +=+ ∴76x = ∴HG=3+72566= 小结：这里的AG=HG 是学生很难发现的结论，可适当引导 本堂课总结知识：解决折叠问题的一般方法P方法：体会方程思想的重要性推广：矩形中的折叠问题作业布置：附配套作业。

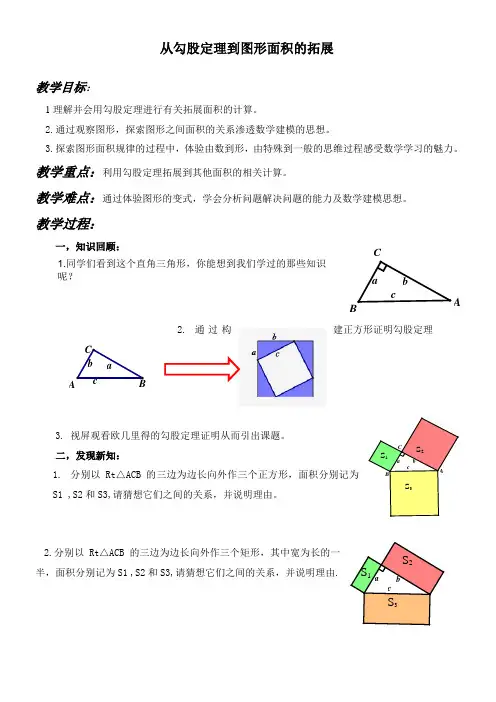
从勾股定理到图形面积的拓展教学目标：1理解并会用勾股定理进行有关拓展面积的计算。

2.通过观察图形，探索图形之间面积的关系渗透数学建模的思想。

3.探索图形面积规律的过程中，体验由数到形，由特殊到一般的思维过程感受数学学习的魅力。

教学重点：利用勾股定理拓展到其他面积的相关计算。

教学难点：通过体验图形的变式，学会分析问题解决问题的能力及数学建模思想。

教学过程：一，知识回顾：2. 通过构建正方形证明勾股定理3. 视屏观看欧几里得的勾股定理证明从而引出课题。

二，发现新知：1. 分别以Rt △ACB 的三边为边长向外作三个正方形，面积分别记为S1 ,S2和S3,请猜想它们之间的关系，并说明理由。

2.分别以Rt △ACB 的三边为边长向外作三个矩形，其中宽为长的一半，面积分别记为S1 ,S2和S3,请猜想它们之间的关系，并说明理由.1.同学们看到这个直角三角形，你能想到我们学过的那些知识呢？cbaC ABcb aCcb aS 1S 2S 3CABcbaS 2S 3S 1练习. 如图是一株美丽的勾股树，其中所有的四边形都是正方形， 所有的三角形都是直角三角形．若正方形A 、B 、C 、D 的面积分别是9、25、4、9，则最大正方形E 的面积是 （ ） A 、13 B 、26 C 、47 D 、942. 分别以Rt △ACB 的三边为边长向外作三个半圆，面积分别记为S1 ,S2和S3,请猜想它们之间的关系，并说明理由。

三，探究新知分别以直角三角形的三边为边向外作其它的某一种图形，面积也满足S1+S2=S3.要求：1.在学习单上尝试画出草图，并写出简要的证明过程;2.先独立思考,再小组交流.cba ABCcb aABCcba ABCcb aABCcbaS 2S 3S 1CAB3.总结归纳运用四，拓展运用：1如图，已知在Rt △ABC 中， ∠ ACB=Rt ∠，AB=4，分别以AC 、BC 为直径作半圆，面积分别记为S1、S2，则S1+S2的是多少?2.如图，分别以Rt △ACB 的三边为直径作三个半圆，三个阴影部分的面积分别记为S1 ,S2和S3, 那么S1 ,S2和S3有什么样的数量关系呢？3.如图，在Rt △ABC 中，∠C=90°，分别以AB 、AC 、BC 为边，在AB 的同侧作正方形ABEF 、ACPQ 、BDMC ，四块阴影部分的面积分别为S1、S2、S3、S4，若S 正方形ABEF=25，S 正方形ACPQ=9，则S1+S2+S3+S4等于（ ）A.12B.15C.18D.20 五，回顾总结cbaS 3S 1S 2CBAS2S1S3S4EFBACc baBa 2 +b 2=c 2s 1+s 2=s 3ACS 2S 1S 2。

浙教版数学八年级上册《阅读材料从勾股定理到图形面积关系的拓展》教学设计1一. 教材分析《阅读材料从勾股定理到图形面积关系的拓展》是浙教版数学八年级上册的一篇阅读材料。

本节课主要通过介绍勾股定理及其在几何图形面积计算中的应用，让学生了解勾股定理的来历，理解勾股定理的本质，掌握运用勾股定理解决一些简单几何图形面积问题的方法。

教材通过丰富的阅读材料，激发学生的学习兴趣，培养学生的阅读理解能力，提高学生运用数学知识解决实际问题的能力。

二. 学情分析学生在七年级时已经学习了勾股定理的定义和证明，对勾股定理有一定的了解。

但部分学生对勾股定理的理解停留在死记硬背上，缺乏深入理解和灵活运用。

此外，学生在之前的学习中已经接触过一些几何图形的面积计算，但对于如何运用勾股定理解决面积问题还不太清楚。

因此，在教学过程中，教师需要帮助学生深化对勾股定理的理解，引导学生将勾股定理与面积计算相结合，提高学生运用数学知识解决实际问题的能力。

三. 教学目标1.了解勾股定理的来历，理解勾股定理的本质。

2.掌握运用勾股定理解决一些简单几何图形面积问题的方法。

3.培养学生的阅读理解能力，提高学生运用数学知识解决实际问题的能力。

4.激发学生的学习兴趣，培养学生的探究精神。

四. 教学重难点1.重点：了解勾股定理的来历，理解勾股定理的本质；掌握运用勾股定理解决一些简单几何图形面积问题的方法。

2.难点：如何引导学生将勾股定理与面积计算相结合，提高学生运用数学知识解决实际问题的能力。

五. 教学方法1.讲授法：教师通过讲解勾股定理的来历、证明和应用，帮助学生了解和掌握勾股定理。

2.阅读理解法：学生通过阅读教材中的阅读材料，提高阅读理解能力，理解勾股定理在面积计算中的应用。

3.实践操作法：学生通过动手操作，解决实际问题，提高运用数学知识解决实际问题的能力。

4.讨论交流法：学生通过小组讨论，分享学习心得，互相学习，提高学习效果。

六. 教学准备1.教材：浙教版数学八年级上册。

浙教版数学八年级上册《阅读材料从勾股定理到图形面积关系的拓展》教案1一. 教材分析《阅读材料从勾股定理到图形面积关系的拓展》是浙教版数学八年级上册的一篇阅读材料。

本节课主要通过介绍勾股定理以及图形面积关系的拓展，让学生了解并掌握勾股定理在解决实际问题中的应用，以及图形面积计算方法的拓展。

教材通过阅读材料的形式，引导学生主动探究，提高学生的数学素养。

二. 学情分析学生在七年级时已经学习了勾股定理，对勾股定理有一定的认识和理解。

但如何在实际问题中应用勾股定理，以及图形面积关系的拓展，可能还不够熟练。

因此，在教学过程中，教师需要引导学生将已知的勾股定理与实际问题相结合，通过探究和解决实际问题，加深对勾股定理的理解和应用。

三. 教学目标1.了解勾股定理在解决实际问题中的应用。

2.掌握图形面积计算方法的拓展。

3.培养学生的数学思维能力和解决问题的能力。

四. 教学重难点1.重点：勾股定理在解决实际问题中的应用，图形面积计算方法的拓展。

2.难点：如何将勾股定理与实际问题相结合，运用图形面积计算方法解决实际问题。

五. 教学方法采用问题驱动法、案例分析法、小组合作法等教学方法。

通过设置问题情境，引导学生主动探究，以实际案例分析为基础，让学生在解决问题的过程中掌握勾股定理的应用和图形面积计算方法的拓展。

六. 教学准备1.准备相关的实际问题案例。

2.准备图形面积计算的相关材料。

3.准备教学PPT。

七. 教学过程1.导入（5分钟）通过一个实际问题情境，如测量一个直角三角形的斜边长度，引导学生回顾勾股定理。

让学生思考：勾股定理在解决这个问题中起到了什么作用？2.呈现（15分钟）呈现一系列与勾股定理相关的实际问题，让学生独立思考并尝试解决。

如：一个直角三角形的两条直角边长分别为3cm和4cm，求斜边长度。

引导学生运用勾股定理解决问题。

3.操练（20分钟）让学生分组合作，探讨并解决更多的实际问题。

如：一个长方形的长和宽分别为8cm和6cm，求长方形的对角线长度。

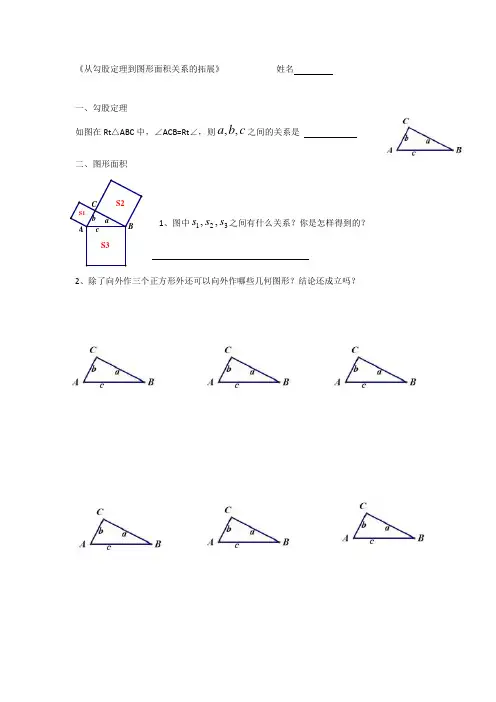
《从勾股定理到图形面积关系的拓展》姓名
一、勾股定理
如图在Rt△ABC中，∠ACB=Rt∠，则,,
a b c之间的关系是
二、图形面积
1、图中123
,,
s s s之间有什么关系？你是怎样得到的？
2、除了向外作三个正方形外还可以向外作哪些几何图形？结论还成立吗？
三、拓展
1. 2.
四、应用
练习1.
如图,已知在Rt△ABC中,∠ACB=Rt∠，AB=4，分别以AC、BC为直径作半圆，
面积分别记为S1、S2，则S1+S2的值等于.
变式：若∠ABC=30°，则S1+S2的值等于.
练习2.
如图，在Rt△ABC中，∠C=90°，分别以AB、AC、BC为边，在AB
的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为
S1、S2、S3、S4，若S正方形ABEF=25，S正方形ACPQ=9，
则S1+S2+S3+S4等于（）
A.12
B.15
C.18
D.20
练习3.
如图，在△ABC中，∠ACB＝90º，AC＞BC，分别以AB、BC、CA为
一边向△ABC外作正方形ABDE、BCMN、CAFG，连接EF、GM、ND，
设△AEF、△BND、△CGM的面积分别为S1、S2、S3，则下列结论正确
的是（）
A．S1＝S2＝S3 B．S1＝S2＜S3
C．S1＝S3＜S2 D．S2＝S3＜S1
练习4.
已知：如图，以Rt△ABC的三边a、b、c为边分别向外作等腰直角三角形．
面积分别为S1、S2、S3，若斜边AB
＝6，则S1+S2为
．。