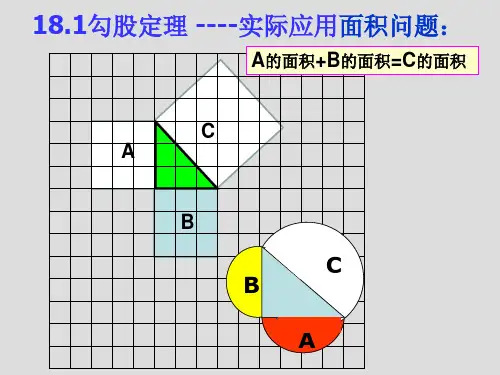
勾股定理与面积法
- 格式:doc
- 大小:38.50 KB
- 文档页数:2

勾股定理解析三角形面积和边长之间的关系勾股定理是初中数学中最基础的知识点之一,它指出:在一个直角三角形中,直角边的长度的平方等于另外两条边的长度平方之和。
用数学符号来表示就是:a² + b² = c²,其中c为斜边的长度,a、b为直角边的长度。
该定理的证明方法有很多种,其中最著名的莫过于毕达哥拉斯的证明。
面积和长度的关系三角形是初中数学中的另一个基础知识点,它有许多性质和公式,例如,三角形的面积可以用底边和高来表示,即面积等于底边长度乘以高的长度再除以2,公式可以表示为:S = 1/2 * a * h。
而在勾股定理中,三角形的斜边可以用另外两条直角边的长度表示,此时三角形的面积可以表示为:S = 1/2 * a * b。
三角形的面积公式中的“底边”和“高”都是用长度表示的,而勾股定理中的“直角边”和“斜边”也是用长度表示的。
这就说明,三角形的面积和边长之间存在着某种关系。
为了探究这种关系,我们可以结合勾股定理和三角形的面积公式来进行推导。
在勾股定理中,有c² = a² + b²,两边同时乘以2再除以c²,可以得到:2S/c² = 2ab/c²这里,S表示三角形的面积,c为斜边的长度,a、b为直角边的长度。
式子左边表示三角形的面积与斜边的平方之间的比值,式子右边表示直角边之积与斜边的平方之间的比值。
进一步移项得到:S = ab/c这就是三角形面积和边长之间的关系式。
结论:在任意一个三角形中,其面积等于底边长度和高的乘积再除以2,也等于任意两边长度之积再除以第三边的长度。
这两个公式是等价的。
结语通过对勾股定理和三角形面积公式的推导过程,我们可以发现它们之间存在着紧密的关系。
这不仅可以加深我们对数学知识的理解,还有助于我们更加灵活地运用它们,更好地解决实际问题。

第1讲勾股定理第一部分知识梳理1.勾股定理:直角三角形的两直角边的平方和等于斜边的平方。
若直角三角形的两条直角边为a、b,斜边为c,则a²+b²=c²。
2.勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a²+b²=c²,那么这个三角形是直角三角形。
3.满足a²+b²=c²的三个正整数,称为勾股数。
若a,b,c是一组勾股数,则ak,bk,ck(k为正整数)也必然是一组勾股数。
常用的几组勾股数有3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41等。
4.勾股定理的应用:①圆柱形物体表面上的两点间的最短距离;②长方体或正方体表面上两点间的最短距离问题。
5.直角三角形的判别:①定义,判断一个三角形中有一个角是直角;②根据勾股定理的逆定理,三角形一边的平方等于另外两边的平方和,则该三角形是直角三角形。
6.勾股定理中的方程思想:勾股定理三角形有一个直角的“形”的特征,转化为三边“数”的关系,因此它是数形结合的一个典范.对于一些几何问题,往往借助于勾股定理,利用代数方法来解决.把一条边的长设为未知数,根据勾股定理列出方程,解方程求出未知数的值,即使有时出现了二次方程,大多可通过抵消而去掉二次项。
7.勾股定理中的转化思想:在利用勾股定理计算时,常先利用转化的数学思想构造出直角三角形,比如立体图形上两点之间的最短距离的求解,解答时先把立体图形转化为平面图形,在平面图形中构造直角三角形求解。
8.拓展:特殊角的直角三角形相关性质定理。
第二部分精讲点拨考点1. 勾股定理【例1】在Rt△ABC中,已知两边长为3、4,则第三边的长为变式1 等腰三角形的两边长为10和12,则周长为______,底边上的高是________,面积是_________。
变式2 等边三角形的边长为6,则它的高是________变式3 在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C所对的边,(1)已知c=4,b=3,求a;(2)若a:b=3:4,c=10cm,求a、b。

面积法验证勾股定理
面积法验证勾股定理是一种基于几何图形面积关系的验证方法。
根据勾股定理,对于任意直角三角形,其斜边平方等于两直角边平方和,即a+b=c。
而面积法验证勾股定理的基本思想是,通过计算直角三角形的三个内切圆的面积,可以得到勾股定理中等号两边的面积之和,从而验证该定理的正确性。
具体方法是,以直角边a和b为直径画两个内切圆,以斜边c为直径画一个外切圆,根据圆的面积公式可得到三个圆的面积分别为πa/4、πb/4和πc/4。
由于勾股定理中等号两边的面积之和为ab/2,因此只需证明πa/4+πb/4=πc/4即可。
通过对比两边的式子,可以发现它们是等价的,因此勾股定理得证。
- 1 -。

勾股定理的面积公式
勾股定理是一个古老的数学定理,它指出,在一个直角三角形中,两条直角边的平方和等于斜边的平方。
它是由古希腊数学家苏格拉底发现的,他发现了一个直角三角形的三条边的长度之间的关系,即勾股定理。
勾股定理的面积公式是:面积=1/2*直角边1*直角边2。
这个公式表明,在一个直角三角形中,两条直角边的乘积除以2,就是该三角形的面积。
勾股定理的面积公式可以用来计算任何直角三角形的面积,只要知道它的两条直角边的长度。
这个公式也可以用来计算任何矩形的面积,因为矩形也是一个特殊的直角三角形,它的两条直角边相等。
勾股定理的面积公式也可以用来计算任何梯形的面积,因为梯形也是一个特殊的直角三角形,它的两条直角边不相等。
只要知道梯形的两条直角边的长度,就可以用勾股定理的面积公式来计算梯形的面积。
勾股定理的面积公式是一个非常有用的数学工具,它可以用来计算任何直角三角形、矩形和梯形的面积。
它的简单性和实用性使它成为一个非常有用的数学工具,它可以帮助我们解决许多实际问题。

勾股定理的计算方法
勾股定理是初中数学中的重要定理,它是指直角三角形中,直角边的平方和等于斜边的平方。
在数学中,我们经常会用到勾股定理来解决各种问题,因此掌握勾股定理的计算方法是非常重要的。
首先,我们来看一下勾股定理的表达式,设直角三角形的两直角边长分别为a、b,斜边长为c,则有a² + b² = c²。
这就是著名的勾股定理公式。
接下来,我们来看一些勾股定理的计算方法。
1. 已知两直角边长,求斜边长,这是最基本的应用,根据勾股定理的公式,直接代入已知的两直角边长,即可求得斜边长。
2. 已知斜边长和一直角边长,求另一直角边长,同样利用勾股定理的公式,将已知的斜边长和直角边长代入,即可求得另一直角边长。
3. 判断三条边长是否构成直角三角形,如果已知三条边长,可以利用勾股定理来判断这三条边长是否构成直角三角形。
只需要将
三条边长代入勾股定理的公式,如果等式成立,则构成直角三角形。
4. 求直角三角形的面积,利用勾股定理可以求直角三角形的面积。
根据公式S=1/2底高,将直角边作为底,另一直角边作为高,
代入勾股定理的公式,即可求得直角三角形的面积。
以上就是勾股定理的一些基本计算方法。
通过掌握这些方法,
我们可以更好地应用勾股定理解决各种数学问题。
在实际生活中,
勾股定理也有着广泛的应用,比如在建筑、工程、地理等领域都可
以看到它的身影。
总之,勾股定理是数学中的重要定理,掌握它的计算方法对我
们的学习和工作都有着积极的影响。
希望大家能够认真学习勾股定理,灵活运用它,提高自己的数学水平。
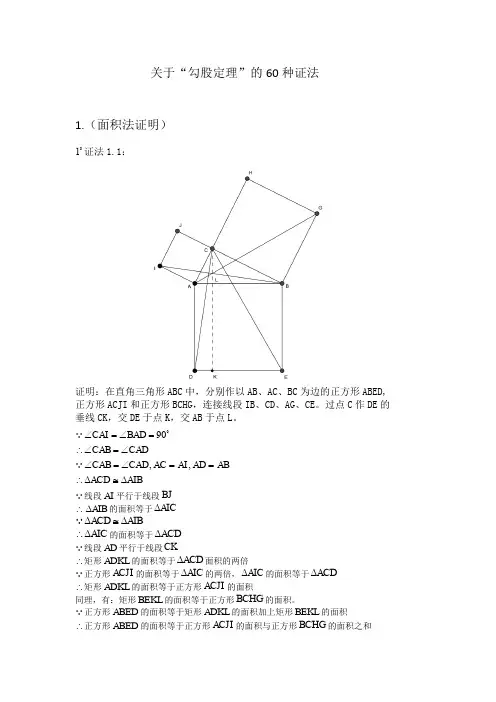
关于“勾股定理”的60种证法1.(面积法证明)1 证法1.1:证明:在直角三角形ABC 中,分别作以AB 、AC 、BC 为边的正方形ABED,正方形ACJI 和正方形BCHG ,连接线段IB 、CD 、AG 、CE 。
过点C 作DE 的垂线CK ,交DE 于点K ,交AB 于点L 。
90,,CAI BAD CAB CADCAB CAD AC AI AD AB ACD AIB∠=∠=∴∠=∠∠=∠==∴∆≅∆线段AI 平行于线段BJ ∴AIB ∆的面积等于AIC ∆ACD AIB ∆≅∆AIC ∴∆的面积等于ACD ∆ 线段AD 平行于线段CK∴矩形ADKL 的面积等于ACD ∆面积的两倍正方形ACJI 的面积等于AIC ∆的两倍,AIC ∆的面积等于ACD ∆ ∴矩形ADKL 的面积等于正方形ACJI 的面积同理,有:矩形BEKL 的面积等于正方形BCHG 的面积。
正方形ABED 的面积等于矩形ADKL 的面积加上矩形BEKL 的面积∴正方形ABED 的面积等于正方形ACJI 的面积与正方形BCHG 的面积之和即222AC BC AB +=.Remark :此为欧几里得(Euclid,约公元前330年-公元前275年)在几何原本中的证明方法。
2 证法1.2:证明:在上图中,整个正方形的面积为2()a b +,又等于四个直角三角形的面积加上里面的小正方形的面积,等于22ab c +。
因此,22()2a b ab c +=+,此即:222a b c +=。
Remark :此证法据Bretschneider 和Hankel 的推测,为毕达哥拉斯(Pythagoras ,约公元前580~约前500)的证法。
3 证法1.3(总统证明法)如图,三角形ABC 与三角形BDE 完全相等,易证三角形ABE 为等腰直角三角形。
整个直角梯形ACDE 的面积为21()2a b +,又等于两个直角三角形的面积加上等腰直角三角形ABE 的面积,等于212ab c +,故2211()22a b ab c +=+。

勾:直角三角形较短的直角边;股:直角三角形较长的直角边;弦:斜边。
1、勾股定理:直角三角形两直角边a ,b 的平方和等于斜边c 的平方,即a 2+b 2=c 2。
2、勾股定理的逆定理:如果三角形的三边长a ,b ,c 有关系a 2+b 2=c 2,那么这个三角形是直角三角形。
3、勾股数:满足a 2+b 2=c 2的三个正整数,称为勾股数。
若是勾股数组,则na 、nb 、nc 也是勾股数组。
4、简单运用:⑴勾股定理——常用于求边长、周长、面积;理解:①已知直角三角形的两边求第三边,并能求出周长、面积。
②用于证明线段平方关系的问题。
③利用勾股定理,作出长为√n 的线段⑵勾股定理的逆定理——常用于判断三角形的形状;理解:①确定最大边(不妨设为c );②若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形;若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边);若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)考点4:折纸问题例1: 如图是一张直角三角形的纸片,两直角边AC=6 cm, BC=8 cm ,现将▲ABC 折叠,使点B 与点A 重合,折痕为DE ,则BE 的长为( )A. 4 cmB. 5 cmC. 6 cmD. 10 cm例2: 如图,在三角形纸片ABC 中,∠C =90°,AC =6,折叠该纸片使点C 落在AB 边上的D 点处,折痕BE 与AC 交与点E ,若AD =BD ,求折痕BE 的长.,,a bc例3:如图,折叠长方形的一边AD,点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,求EC的长.例4:一张长方形纸片宽AB=8 cm,长BC=10 cm.现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),求EC的长.例5 、如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为.例6如图,动手操作:在矩形纸片ABCD中,AB=3,AD=5.折叠纸片,使点A落在BC 边上的A'处,折痕为PQ,当点A'在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A'在BC边上可移动的最大距离为_______.例7如图,矩形纸片ABCD中,AB=5cm,BC=10cm,CD上有一点E,EC=2cm,AD上有一点P,PA=6cm,过点P作PF⊥AD交BC于点F,将纸片折叠,使P与E重合,折痕交PF 于Q,则线段PQ的长是___cm.例8如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将▲ABP沿BP翻折至▲EBP,PE与CD相交于点O,且OE=OD,BE与CD交于点G.(1)求证:AP=DG;(2)求线段AP的长.例9.如图,在直角坐标系中,长方形纸片ABCD的边AB∥CO,点B坐标为(8,4),若把图形按如图所示折叠,使B、D两点重合,折痕为EF.(1)求证:△DEF为等腰三角形;(2)求折痕EF的长.考点5:面积相关(等面积法)例1:△ABC是等边三角形,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F,BN⊥AC于点N,则DE、DF、BN三者的数量关系为▲;例2:如图,在Rt△ABC中,∠ACB=90°,CD是高,AC=5,BC=12,求CD的长度。

勾股定理面积水的证明方法嘿,朋友们!今天咱来聊聊那个超厉害的勾股定理面积水的证明方法呀!咱先说说勾股定理是啥,就是在一个直角三角形里,两条直角边的平方和等于斜边的平方。
就好像一个直角三角形,短的那条边是 3,长的那条边是 4,那斜边肯定就是 5 啦,因为 3 的平方加上 4 的平方正好等于 5 的平方嘛。
那怎么用面积水的方法来证明呢?咱可以想象一下啊,有这么一个直角三角形,咱给它外面围上三个正方形,这三个正方形的边长分别就是三角形的三条边呀。
然后呢,咱就开始玩水啦!哈哈,开个玩笑,其实就是通过计算这些正方形的面积来找到勾股定理的证据。
你看啊,那个以斜边为边长的大正方形的面积,是不是可以分成几个部分呀?一部分就是以直角边为边长的两个小正方形的面积,还有一部分呢,就是几个三角形的面积。
这不就有意思了嘛!咱就拿一个具体的例子来说吧。
假如直角边一个是 3,一个是 4,那以3 为边长的正方形面积就是9,以4 为边长的正方形面积就是16。
那大正方形的面积不就是 9 加上 16 嘛,等于 25。
然后你再想想,大正方形里面那几个三角形的面积加起来是不是也有一定的值呀。
这不就像是搭积木一样嘛,把这些面积的块块拼来拼去,最后就能发现勾股定理的奥秘啦!是不是很神奇?你说数学咋这么好玩呢!咱再深入想想,要是没有勾股定理,那好多建筑可就没法盖得稳稳当当啦,那些高楼大厦说不定就歪歪斜斜的了,多吓人呀!所以说呀,这个小小的定理用处可大着呢。
用面积水的证明方法,就像是在数学的海洋里畅游,一点点地探索,一点点地发现。
就好像我们在寻找宝藏一样,每一个新的发现都让我们兴奋不已。
这就是勾股定理面积水的证明方法呀,是不是很有趣?是不是让你对数学又多了一份喜爱呢?大家都快去试试吧,感受一下数学的魅力!别再觉得数学枯燥啦,其实它里面藏着好多好玩的东西等着我们去发现呢!。

勾股定理及其应用勾股定理,也被称为毕达哥拉斯定理,是数学中一个重要的几何定理,被广泛应用于各个领域。
本文将介绍勾股定理的原理和证明,并介绍其在实际应用中的一些重要示例。
一、勾股定理的原理和证明勾股定理是一个关于直角三角形斜边与两个直角边的关系定理。
它的表述可以归纳为:在直角三角形中,斜边的平方等于两个直角边的平方和。
设直角三角形的斜边长度为c,两个直角边的长度分别为a和b。
根据勾股定理,有c² = a² + b²。
证明该定理的方法多种多样,其中一种比较简单的方法是利用面积关系进行证明。
假设直角三角形的两条直角边分别为a和b,斜边为c。
将该三角形移动到一个边长为a、边宽为b的矩形内,如图1所示。
[图1:勾股定理证明过程的示意图]显然,通过镜像方式将三角形补全,可以构成一个边长为c、边宽为c的正方形,如图2所示。
[图2:利用镜像补全三角形后构成正方形]由于正方形的面积等于边长的平方,我们可以得到两个式子:面积1 = a * b面积2 = c * c由于直角三角形的面积1等于正方形的面积2,我们可以得到:a *b =c * c进一步变换可得:c² = a² + b²上述证明过程说明了勾股定理的原理,并证明了定理的正确性。
二、勾股定理的应用示例勾股定理在实际生活中有着广泛的应用,下面将介绍其中一些重要的示例。
1. 测量直角三角形的边长勾股定理可以被用于测量直角三角形的边长。
当我们已知一个直角三角形的两个直角边的长度时,可以通过勾股定理计算出斜边的长度。
例如,如果直角三角形的两个直角边的长度分别为3和4,可以使用勾股定理计算出斜边的长度:c² = 3² + 4²c² = 9 + 16c² = 25c = 5因此,该直角三角形的斜边长度为5。
2. 建筑和工程应用勾股定理在建筑和工程领域中具有重要的应用。

面积证明勾股定理方法一:将四个全等的直角三角形拼成如图(1)所示的正方形。
图(1)中,所以。
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形。
图(2)中,所以。
方法三:将四个全等的直角三角形分别拼成如图(3)—1和(3)—2所示的两个形状相同的正方形。
在(3)—1中,甲的面积=(大正方形面积)—(4个直角三角形面积),在(3)—2中,乙和丙的面积和=(大正方形面积)—(4个直角三角形面积),所以,甲的面积=乙和丙的面积和,即:.方法四:如图(4)所示,将两个直角三角形拼成直角梯形。
,所以。
C B AD EF1 如图,圆柱的高为10 cm ,底面半径为2 cm.,在下底面的A 点处有一只蚂蚁,它想吃到上底面上与A 点相对的B 点处,需要爬行的最短路程是多少?2 如图,长方体的高为3 cm ,底面是边长为2 cm 的正方形. 现有一小虫从顶点A 出发,沿长方体侧面到达顶点C 处,小虫走的路程最短为多少厘米? 答案AB=5AB3、一只蚂蚁从棱长为1的正方体纸箱的B’点沿纸箱爬到D 点,那么它所行的最短路线的长是_____________。
4、如图,小红用一张长方形纸片ABCD 进行折纸,已知该纸片宽AB 为8cm ,•长BC •为10cm .当小红折叠时,顶点D 落在BC 边上的点F 处(折痕为AE ).想一想,此时EC 有多长?•5.如图,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,则EB 的长是( ). A .3B.4 CD .56.已知:如图,在△ABC 中,∠C=90°,∠B=30°,AB 的垂直平分线交BC 于D ,垂足为E ,BD=4cm .求AC 的长.7、如图,有一个直角三角形纸片,两直角边AC=6,BC=8,现将直角边AC 沿直线AD 折叠,使其落在斜边AB 上,且与AE 重合,则CD 的长为8、如图,在矩形ABCD 中,,6=AB 将矩形ABCD 折叠,使点B 与点D 重合,C 落在C '处,若21::=BE AE ,则折痕EF 的长为 。
勾股定理的五种验证方法
嘿,朋友们!今天咱来聊聊勾股定理那超有趣的五种验证方法呀!
你说勾股定理像不像一个神秘的宝藏,等着我们去挖掘它的秘密呢?
第一种方法,拼图法。
就好像我们在玩拼图游戏一样,把不同的图形拼在一起,突然!哇塞,就发现了勾股定理的奥秘。
你看,把几个直角三角形和正方形巧妙地组合,就像变魔术一样,神奇地得出了那个经典的关系。
这难道不令人惊叹吗?
第二种方法呢,是面积法。
这就好像我们在比较不同区域的大小,通过计算各种图形的面积,嘿,勾股定理就冒出来啦!是不是很有意思呀?
再来说说第三种,相似三角形法。
这就好比在一群人中找到相似的小伙伴,然后从他们的关系中发现了勾股定理这个大秘密。
还有第四种,射影定理法。
哎呀呀,就像是一束光照射下来,影子中隐藏着勾股定理的线索呢。
最后一种,赵爽弦图法。
这可是咱老祖宗的智慧结晶呀!看着那复杂又精美的图案,就知道里面蕴含着多么深刻的道理。
你想想,这些方法就像一把把钥匙,打开了勾股定理这个神秘宝盒。
每一种方法都有它独特的魅力和乐趣,不是吗?我们可以通过拼图感受创造的快乐,可以通过面积计算体会数学的严谨,可以从相似三角形中找到规律的美妙,可以在射影定理中探索光与影的奇妙联系,还可以从赵爽弦图中领略古人的智慧。
数学的世界就是这么神奇呀!勾股定理不仅仅是一个定理,更是人类智慧的结晶。
它在我们的生活中无处不在,从建筑设计到航天工程,都有它的身影呢。
所以呀,别小看了这小小的勾股定理和它的验证方法,它们可是有着大大的能量呢!让我们一起在数学的海洋里尽情遨游,去发现更多的奇妙之处吧!。
中国古代证明勾股定理的方法
中国古代证明勾股定理的方法可以追溯到《周髀算经》中的《开方》篇。
该篇中,推导了勾股定理的一部分内容,即若直角边和斜边的长度已知,则可求另一直角边的长度,但并未给出具体的证明方法。
后来,中国古代数学家张丘建提出了一种证明勾股定理的方法,即用面积法证明。
他认为,一个直角三角形的面积由两个小正方形和一个大正方形组成,其中大正方形面积为斜边长度的平方,两个小正方形面积分别为两条直角边的长度的平方。
因此,可以通过比较三个正方形的面积关系,推导出勾股定理的正确性。
此外,中国古代还有一些其他的证明勾股定理的方法,比如利用《周筆算經》中的“勾股数”和“勾股数形”等。
还有一些工具方法,如“海岛法”“古希腊做图法”等,也被用来证明勾股定理。
16CB 勾股定理与面积法学习目标:熟练应用勾股定理和面积法列方程解决求值问题。
培养化归思想和方程思想。
学习过程:例1学习:如图,Rt △ABC 的两直角边为3,4。
求斜边上的高CD 。
A BD归纳:我们有Rt △ABC 的两种面积表示方法BC AC •21和 。
像这样,用两种面积表示方法表示同一图形的面积,从而建立方程来解决问题的方法叫面积法.....练习:如图,Rt △ABC 的一直角边为5,斜边长13。
求斜边上的高CD 。
C A BD例2学习:如图,等腰三角形的三边为17㎝,17㎝,16㎝。
求腰上的高CD 。
分析:由CD 为高想到此三角形的面积可以表示为CD AB •21,如果知道BC 边上的高,就可以用面积法建立方程求出CD 。
解:作BC 边上的高AE 。
∵AE 为等腰三角形底边上的高∴AE 为底边BC 的中线 ( ) ∴CE=55CA B BACDD练习:如图,等腰三角形的腰长为17㎝,底边上的高AE 为15㎝。
求腰上的高CD 。
例3学习:等腰三角形的腰长为5,面积为12。
求它的底边BC 的长。
首先我们想到:根据面积可以求出腰上的高,但是腰上的高是在三角形的内部还是外部呢?看来我们要分两种情况。
先求出CD=4.8,然后求出AD= 再求出BD= 或 最后求出BC= 或接下来我们想一想等腰三角形三线合一的性质,我们可以作底边的高构造直角三角形,就不需要分类了。
我们可以根据面积列一个方程,还可以根据勾股定理列一个方程。
由方程组可以解决这个问题。
解:作BC 边上的高AE 。
∵AE 为等腰三角形底边上的高∴AE 为底边BC 的中线 ( )设BE=x=CE,AE=y. (注意2x 的值才是要 求的答案) 由Rt △AEC 得 =+22y x 由三角形面积得 =xy 练习:5BAC EAB1.设直角三角形的三边为a ,b ,c ,斜边c 上的高为h 。
(1)a=6,b=8,求h (2)a=5,c=13,求h (3)b=24,c=25,求h2.三角形的三边长如图所示,求BC 边上的高。
勾股定理20种证明方法勾股定理是中国古代数学中的一个重要定理,也被称为勾股三角形定理,它是指直角三角形中,直角边的平方等于两直角边的平方和。
勾股定理的发现和证明有很多方法,下面我们来看看20种不同的证明方法。
1. 几何方法:这是最常见的证明方法,可以通过绘制直角三角形,然后运用几何知识来证明。
2. 代数方法:可以通过代数运算来证明,将直角三角形的三边长度表示为变量,然后通过代数运算得出结论。
3. 物理方法:可以利用物理学知识,比如平面几何法,来证明勾股定理。
4. 数学归纳法:可以运用数学归纳法来证明勾股定理,将直角三角形的边长依次递增,然后证明其中一个等式成立,推导出其他情况。
5. 解析几何法:可以通过解析几何的方法,利用坐标系和直线方程来证明勾股定理。
6. 函数法:可以通过函数图像和函数性质来证明勾股定理。
7. 同余定理方法:可以通过同余定理来证明勾股定理。
8. 三角函数方法:可以运用三角函数的性质和公式来证明勾股定理。
9. 相似三角形方法:可以通过相似三角形的性质来证明勾股定理。
10. 斜率方法:可以运用直线的斜率来证明勾股定理。
11. 反证法:可以通过反证法来证明勾股定理,假设直角三角形的三边不符合勾股定理,然后推导出矛盾。
12. 三角形面积法:可以通过计算直角三角形的面积来证明勾股定理。
13. 欧拉定理法:可以通过欧拉定理来证明勾股定理。
14. 空间几何法:可以将直角三角形的顶点放置在空间中,运用空间几何知识来证明勾股定理。
15. 弦与切线相交定理:可以利用弦与切线相交的性质来证明勾股定理。
16. 数列方法:可以通过构造数列,运用数列的性质来证明勾股定理。
17. 微积分方法:可以通过微积分的知识来证明勾股定理。
18. 统计方法:可以通过统计实验来证明勾股定理,比如通过大量的直角三角形数据验证勾股定理成立。
19. 推广方法:可以通过勾股定理的推广形式来证明勾股定理,比如勾股定理的逆定理。
20. 全等三角形法:可以通过全等三角形的性质来证明勾股定理。
17
16
C
A
B D
勾股定理与面积法
学习目标:熟练应用勾股定理和面积法列方程解决求值问题。
培养化归思想和方程思想。
学习过程:
例1学习:如图,Rt △ABC 的两直角边为3,4。
求斜边上的高CD 。
3
4
A B
D
归纳:我们有Rt △ABC 的两种面积表示方法
BC AC •2
1
和 。
像这样,用两种面积表示方法表示同一图形的面积,从而建立方程来解决问题的方法叫面积法..... 练习:如图,Rt △ABC 的一直角边为5,斜边长13。
求斜边上的高CD 。
5
C A B
D
例2学习:如图,等腰三角形的三边为17㎝,17㎝,16㎝。
求腰上的高CD 。
分析:由CD 为高想到此三角形的面积可以表示为CD AB •21
,如果知道BC 边上的高,就可以用面积法建立方程求出CD 。
解:作BC 边上的高AE 。
∵AE 为等腰三角形底边上的高
∴AE 为底边BC 的中线 ( ) ∴CE=
练习:如图,等腰三角形的腰长为17㎝,底边上的高AE 为15㎝。
求腰上的高CD 。
C
B B
C
A
B
例3学习:等腰三角形的腰长为5,面积为12。
求它的底边BC 的长。
首先我们想到:根据面积可以求出腰上的高,但是腰上的高是在三角形的内部还是外部呢?看来我们要分两种情况。
先求出CD=4.8,然后求出AD= 再求出BD= 或 最后求出BC= 或
接下来我们想一想等腰三角形三线合一的性质,我们可以作底边的高构造直角三角形,就不需要分类了。
我们可以根据面积列一个方程,还可以根据勾股定理列一个方程。
由方程组可以解决这个问题。
解:作BC 边上的高AE 。
∵AE 为等腰三角形底边上的高 ∴AE 为底边BC 的中线 ( ) 设BE=x=CE,AE=y. (注意2x 的值才是要 求的答案)
由Rt △AEC 得 =+22y x 由三角形面积得 =xy 练习:
1.设直角三角形的三边为a ,b ,c ,斜边c 上的高为h 。
(1)a=6,b=8,求h (2)a=5,c=13,求h (3)b=24,c=25,求h
2.三角形的三边长如图所示,求BC 边上的高。
3.三角形ABC 中,AB=24,AC=13,∠B=30度。
求BC 的长。
(先把图形画出来)
B
C
E
4
A
C B。