高中化学常见计算方法及练习：十字交叉法

一、十字交叉相乘法这是利用化合价书写物质化学式的方法，它适用于两种元素或两种基团组成的化合物。

其根据的原理是化合价法则：正价总数与负价总数的代数和为0或正价总数与负价总数的绝对值相等。

现以下例看其操作步骤。

二、十字交叉相比法我们常说的十字交叉法实际上是十字交叉相比法，它是一种图示方法。

十字交叉图示法实际上是代替求和公式的一种简捷算法，它特别适合于两总量、两关系的混合物的计算(即2—2型混合物计算)，用来计算混合物中两种组成成分的比值。

三、十字交叉消去法十字交叉消去法简称为十字消去法，它是一类离子推断题的解法，采用“十字消去”可缩小未知物质的范围，以便于利用题给条件确定物质，找出正确答案。

其实十字交叉法就是解二元一次方程的简便形式如果实在不习惯就可以例方程解但我还是给你说说嘛像A的密度为10 B的密度为8 它们的混合物密度为9 你就可以把9放在中间把10 和8 写在左边标上AB 然后分别减去9 可得右边为1 1 此时之比这1:1 了这个例子比较简单但难的也是一样你自己好好体会一下嘛这个方法其实很好节约时间特别是考理综的时候其实十字交叉法就是解二元一次方程的简便形式如果实在不习惯就可以例方程解但我还是给你说说嘛像A的密度为10 B的密度为8 它们的混合物密度为9 你就可以把9放在中间把10 和8 写在左边标上AB 然后分别减去9 可得右边为1 1 此时之比这1:1 了这个例子比较简单但难的也是一样你自己好好体会一下嘛这个方法其实很好节约时间特别是考理综的时候（一）混和气体计算中的十字交叉法【例题】在常温下，将1体积乙烯和一定量的某气态未知烃混和，测得混和气体对氢气的相对密度为12，求这种烃所占的体积。

【分析】根据相对密度计算可得混和气体的平均式量为24，乙烯的式量是28，那么未知烃的式量肯定小于24，式量小于24的烃只有甲烷，利用十字交叉法可求得甲烷是0.5体积（二）同位素原子百分含量计算的十字叉法【例题】溴有两种同位素，在自然界中这两种同位素大约各占一半，已知溴的原子序数是35，原子量是80，则溴的两种同位素的中子数分别等于。

高中化学计算题解题方法----差量法,极值法,转换法,十字交叉法高中化学计算题解题方法----差量法,极值法,转换法,十字交叉法..主要,差量法是依据化学反应前后的某些“差量”（固体质量差、溶液质量差、气体体积差、气体物质的量之差等）与反应物或生成物的变化量成正比而建立的一种解题法。

此法将“差量”看作化学方程式右端的一项，将已知差量（实际差量）与化学方程式中的对应差量（理论差量）列成比例，其他解题步骤与化学方程式列比例式解题完全一致。

用差量法解题的关键是正确找出理论差量。

【适用条件】（1）反应不完全或有残留物。

在这种情况下，差量反映了实际发生的反应，消除了未反应物质对计算的影响，使计算得以顺利进行。

（2）反应前后存在差量，且此差量易求出。

这是使用差量法的前提。

只有在差量易求得时，使用差量法才显得快捷，否则，应考虑用其他方法来解。

【用法】A ～B ～Δxa b a-bc d可得a/c=(a-b)/d已知a、b、d即可算出c=a*d/(a-b)化学方程式的意义中有一条：化学方程式表示了反应前后各物质间的比例关系。

这是差量法的理论依据。

【证明】设微观与宏观间的数值比为k.（假设单位已经统一）A ～B ～Δxa b a-ba*k b*k (a-b)*k可得a*k=a*[(a-b)]*k/(a-b)推出a/(a*k)=(a-b)/[(a-b)*k]用c替换a*k，d替换(a-b)*k已知a、b、d即可算出c=a*d/(a-b)因此差量法得证【原理】在化学反应前后，物质的质量差和参加该反应的反应物或生成物的质量成正比例关系，这就是根据质量差进行化学计算的原理。

【步骤】1．审清题意，分析产生差量的原因。

2．将差量写在化学反应方程式的右边，并以此作为关系量。

3．写出比例式，求出未知数。

【分类】（一）质量差法例题：在1升2摩/升的稀硝酸溶液中加入一定量的铜粉，充分反应后溶液的质量增加了13.2克，问：（1）加入的铜粉是多少克？（2）理论上可产生NO气体多少升？（标准状况）分析：硝酸是过量的，不能用硝酸的量来求解。

十字交叉的应用技巧 金点子： 对于二元混合物，如果用C 表示己知的两个量C 1、C 2的平均值，n 1、n 2表示C 1、C 2对应的份数，则有：C 1 n 1 + C 2 n 2 = C (n 1 + n 2) = C n 1 + C n 2n 1(C 1 - C ) = n 2 ( C - C 2 ) ,根据这个关系可以写成十字交叉图式：(斜看差数，横看结果)这种运算方法叫十字交叉法。

在运算时，C 必须是已知量或可间接求得的量。

通过十字交叉法可求得C 1与C 2间的物质的量之比。

经典题：例题1 ：（1999年全国高考）原计划实现全球卫星通讯需发射77颗卫星，这与铱(Ir)元素的原子核外电子数恰好相等,因此称为“铱星计划”。

(1)已知铱的一种同位素是19177Ir,则其核内的中子数是 ( )A ．77B ．114C ．191D ．268(2)已知自然界中铱有两种质量数分别为191和193的同位素，而铱的平均原子量为192.22，这两种同位素的原子个数比应为 ( )A ．39︰61B ．61︰39C ．1︰1D ．39︰11方法：（1）可利用“质量数＝质子数+中子数”求解，（2）利用“十字交叉”求解。

捷径：（1）根据“质量数＝质子数+中子数”知：中子数＝191－77＝114。

选B 。

（1） 利用“十字交叉”可得：以此19177Ir 与19377Ir 两种同位素的原子个数比为：0.78︰1.22=39︰61，得答案为A 。

总结： 该题在当年高考中为两条选择题。

若能巧用“十字交叉”，便能迅速获解。

例题2 ：（1999年上海高考）由CO 2、H 2、和CO 组成的混合气在同温同压下与氮气的密度相同。

则该混合气中CO 2、H 2、和CO 的体积比为 ( )A ．29︰8︰13B ．22︰1︰14C ．13︰8︰29D ．26︰16︰57方法：将题中三种气体的式量与氮气的式量作比较，找出其间的联系，然后用“十字交叉”求解。

巧用“十字交叉法”解化学计算题“十字交叉法”是解决具有平均含义的混合物计算题的一种很好的方法。

适用于能列出一个二元一次方程组来求解的命题。

尤其是某些缺少数据而不能直接求解的混合物的判断题，应用平均值的思想先作判断，再用十字交叉法进行推算，可以在短时间内快速解题，运用起来非常简捷。

1 “十字交叉法”的理论依据：数学上的二元一次方程组： x 1 + x2 === 1a 1 由上述方程组可解得： 即十字交叉：其中，a 1 、a 2分别代表单独的化学量，a 平 代表平均的化学量 ，x 1、x 2 分别代表××分数。

2 举例说明“十字交叉法”适用范围及解典型的化学计算题2.1 物质的质量分数“十字交叉”---- 得物质的质量比如果a 1 、a 2 分别代表单独物质的质量分数，a 平 为 混合的 质量分数，则x 1 /x 2 === 物 质 的 质 量 比。

例1：在氯化铵样品中混有下列一种杂质，经测知样品含氮25.7%（质量分数），下列叙述正确的是A ．样品中含NH 4Cl 90%，杂质为尿素B ．样品中含NH 4Cl 70%，杂质为尿素C ．样品中含NH 4Cl 80%，杂质为硫铵D ．样品中含NH 4Cl 90%，杂质为硫铵[解析]样品中含氮质量分数应该是NH 4Cl 和杂质中氮的质量分数的平均值。

已知样品中含氮25.7%，而NH 4Cl 、CO(NH 2)2、(NH 4)2SO 4的氮的质量分数分别是26.2%、46.7%、21.2%。

解法1：常规方法。

设样品为100 g ，样品中含N 25.7%，经求算NH 4Cl 、CO(NH 2)2、(NH 4)2SO 4的氮的质量分数分别是26.2%、46.7%、21.2%。

A ．样品中含NH 4Cl 90%，尿素占10%，则样品中含N 元素：100 g ×90%×26.2%+100 g ×10%×46.7%＝28.25 g ≠25.7 g 。

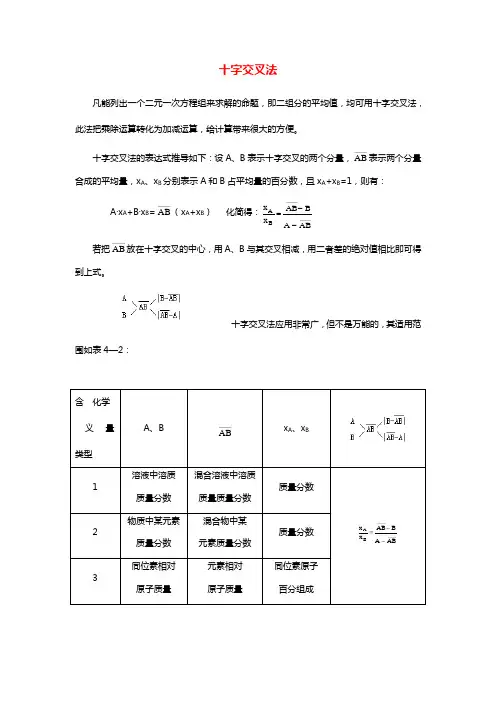
十字交叉法凡能列出一个二元一次方程组来求解的命题，即二组分的平均值，均可用十字交叉法，此法把乘除运算转化为加减运算，给计算带来很大的方便。

十字交叉法的表达式推导如下：设A 、B 表示十字交叉的两个分量，AB ——表示两个分量合成的平均量，x A 、x B 分别表示A 和B 占平均量的百分数，且x A +x B =1，则有： A ·x A +B ·x B =AB ——（x A +x B ） 化简得：x x AB B A ABA B =--———— 若把AB ——放在十字交叉的中心，用A 、B 与其交叉相减，用二者差的绝对值相比即可得到上式。

十字交叉法应用非常广，但不是万能的，其适用范围如表4—2：含 化学义 量类型A 、B AB —— x A 、x B 1 溶液中溶质质量分数混合溶液中溶质质量质量分数 质量分数 x x AB B A AB A B =--———— 2 物质中某元素质量分数混合物中某 元素质量分数 质量分数 3 同位素相对原子质量 元素相对 原子质量 同位素原子百分组成正确使用十字交叉法解题的关键在于：（1）正确选择两个分量和平均量；（2）明确所得比为谁与谁之比；（3）两种物质以什么为单位在比。

尤其要注意在知道质量平均值求体积或物质的量的比时，用此法并不简单。

1. 现有50g 5%的CuSO4溶液，把其浓度增大一倍，可采用的方法有：（1）可将原溶液蒸发掉g水；（2）可向原溶液中加入12.5% CuSO4溶液g；（3）可向原溶液中加入胆矾g；（4）可向原溶液中加入CuSO4白色粉末g。

2 . 今有NH4NO3和CO(NH2)2混合化肥，现测得含氮质量分数为40%，则混合物中NH4NO3和CO(NH2)2的物质的量之比为（）（A）4∶3 （B）1∶1 （C）3∶4 （D）2∶33. （1）已知溶质质量分数分别为19x%和x%的两硫酸溶液，若将它们等体积混和，则所得混和液的溶质质量分数与10x的大小关系如何？（2）已知溶质质量分数为a%的氨水物质的量浓度是b mol·L-1，则a2%的氨水物质的量浓度与b2mol·L-1的大小关系如何？4. 将金属钠在空气中燃烧，生成Na2O与Na2O2的混合物。

化学计算方法十字交叉法“十字交叉法”计算式的差值比凡涉及两个组分量，具有一个平均值的题型可采用“十字交叉法”求解。

但在求解过程中，把所得差值量比的含义搞错的屡见不鲜。

笔者拟定以下几个题型举例分析说明之。

“十字交叉法”的含义可这样理解：上述所得差值量的单位应与基本量的单位相同，但两差量的比不一定是原基本量(如浓度、体积等)的比。

1．求质量比的计算【例1】1体积98%的浓硫酸(密度为1.84g/cm3)与4体积水(密度为1g/cm3)混和，求所得硫酸的百分比浓度。

分析：该题属于两个组分量(98%和0%)求平均值(设为a%)的计算，可采用“十字交叉法”计算。

平均值的含义为“100g混和溶液中含ag硫酸”。

所以所得差值之比为溶液质量之比。

【解】设混和后溶液百分比浓度的a%基本量是溶液的质量，差值之比是浓H2SO4和水的质量之比。

即：a：(98－a)=(1某1.84)∶(4某1)解得a=30.9答：所得H2SO4的百分比浓度为30.9%2．求溶液体积比的计算【例】5mL浓度为1mol/L的烧碱溶液，可稀释成0.05mol/L的烧碱溶液多少毫升？分析：本题属于两个组分量(1mol/L和0mol/L)求平均值(0.05mol/L)的计算，可用“十字交叉法”计算。

平均值含义为“1L稀溶液含NaOH0.05mol”。

所以求出的差量之比为溶液的体积比。

【解】这里差值之比0.05∶(1－0.05)=1∶19显然是浓NaOH溶液和水的体积之比。

设混和后0.05mol/L溶液体积为VmL，有：1∶(1+19)=5∶VV=5某20=100答：可稀释成0.05mol/L的烧碱溶液100mL。

3．求物质的量之比(或气体体积比)的计算【例】相同状况下，11.2L乙烷和丁烷的混合气体完全燃烧，需要47.6L氧气，则混合气体中乙烷和丁烷的物质的量之比为多少？分析：本题平均量含义为：11.2L混合气完全燃烧需47.6L氧气”。

所以求出的差量之比为气体的体积之比或物质的量之比。

一、“十字交叉法”的使用有一定的要求：1、适用于2种物质组成的混合物的计算2、符合关系式：a ·x+ b ·y =c ·(x+y)ax (c-b 或b-c)使差值为正即可c(平均值)b y (a-c 或c-a) 使差值为正即可几点说明：1、若a 、b 为两气体的摩尔质量(相对分子质量)，c 为平均摩尔质量，则x ：y 为混合气体中两种组分的体积比或物质的量之比。

2、若a 、b 为元素的相对原子质量，c 为平均相当原子质量，则x ：y 为元素原子个数比或物质的量之比。

3、若a 、b 、c 为溶液的质量分数，则x ：y 为溶液的质量比。

4、若a 、b 、c 为溶液的物质的量浓度，则x ：y 为溶液的体积比。

十字交叉法”经常出现的有以下几种情况：（一）有关平均摩尔质量的计算M 1·n 1 + M 2·n 2 =·(n 1+n 2) M 1—M 2M 2 M 1—例题1、已知N 2、O 2混合气体的平均摩尔质量为28.8g/mol ，求：混合气体中N 2、O 2的物质的量之比？解析：N 2 28 3.228.8O 2 32 0.8n(N 2):n(O 2) = 3.2:0.8 = 4:1例题2、在标准状况下，由H 2和O 2组成的混合气体的密度等于0.536g/L ，求该混合气体中H 2和O 2的体积比等于多少？n 1—M 2 = n 2 M 1—解析：= ρ·Vm =0.536g/L·22.4L/mol = 12g/molH2 2 20O232 10V(H2):V(O2) = n(H2):n(O2) = 20:10 = 2:1（二）同位素原子的个数比例题3：已知自然界中铱有两种质量数分别为191和193的同位素，而铱的平均原子量为192.22，则这两位种同位素的原子个数比A、39：61B、61：39C、1：1D、39：11解析：191Ir 191 0.78192.22193Ir 193 1.22n(191Ir):n(191Ir) = 0.78:1.22 = 39:61答案：A（三）关于溶液的质量分数的计算m1·ω1+ m2·ω2= (m1+m2)·ω3m1ω3—ω2=m2ω1—ω3例题4、现有20％和5％的两种盐酸溶液，若要配制15％的盐酸溶液，两种盐酸溶液的质量比为多少？解析：20％HCl 20 10155％HCl 5 5m(20％HCl):m(5％HCl) = 10:5 = 2:1例5：实验室用密度为1.84克/厘米398%的浓硫酸与密度为1.1克/厘米3 15%的稀硫酸混和配制密度为1.4克/厘米3 59%的硫酸溶液, 取浓、稀硫酸的体积比最接近的值是A. 1:2B. 2:1C. 3:2D. 2:3[分析] 98 44\ 59 // \ 其体积比为 : 44/1.84 : 39/1.1 ≈ 2:315 39 答案为 D根据溶质质量守恒, 满足此式的是98%X + 15% Y = 59%(X+Y)X 和 Y 之比是溶液质量比,故十字交叉得出的是溶液质量比为44 : 39 ,再换算成体积比（四）关于溶液的物质的量浓度的计算（若溶液混合体积可以相加）c1·V1+ c2·V2= c3·(V1+V2)V1c3—c2=V2c1—c3例题6、物质的量浓度分别为6mol/L和1mol/L的硫酸溶液，按怎样的体积比混合才能配成4mol/L的溶液?解析：6mol/L H2SO4 6 341mol/L H2SO4 1 2V(6mol/L H2SO4):V(1mol/L H2SO4) = 3:2五、用两种物质中同一元素的质量分数求两物质的质量比例7：FeO 中和FeBr2的混合物中Fe 的质量百分率为50%，求两物质的质量比（13∶15）解：FeO 7/9 13/54 13╲╱——1/2 ——╱╲FeBr27/27 5/18 15。

十字交叉法十字交叉法是进行二组分混和物平均量与组分量计算的一种简便方法。

凡是一般的二元一次方程组（a1X + a2Y = a3( X +Y )关系式）的习题，均可用十字交叉法，但受我们所学知识的条件限制，这里只介绍其中的几种。

一、用组分的式量与混合气的平均式量做十字交叉，求组分体积比或含量。

例1：已知H2和CO 的混合气，其平均式量是20，求混合气中H2和CO 的体积比。

（4∶9）解：H2 2 28－20 4╲╱——20 ——╱╲CO 28 20－2 9例2：已知CO、CO2混合气的平均式量是32，耱混合气中CO 的体积百分数。

（75%）解：CO 28 12 3╲╱——32 ——╱╲CO228 4 1二、用同位素的原子量或质量数与元素原子量作交叉，求原子个数比或同位素百分数。

例3：已知铜有63Cu 和65Cu 两种同位素，铜元素的原子量是63.5，求63Cu 和65Cu的原子个数比。

（3∶1）解：63Cu 63 1.5 3╲╱——63.5 ——╱╲65Cu 65 0.5 1三、用组分的气体密度与混合气的密度作十字交叉，求组分的体积比或体积分数。

例4：标况下，氮气的密度为1.25 g·L-1，乙烷的密度为1.34 g·L-1，两种气体混合后，其密度为1.30 g·L-1，求混合气中氮气和乙烷的体积比（4∶5）解：氮气 1.25 0.04 4╲╱—— 1.30 ——╱╲乙烷 1.34 0.05 5四、用两种不同浓度溶液的质量分数与混合溶液的质量分数作十字交叉，求两种溶液的质量比例5：用60%和20%的两种NaOH 溶液混合配成30%的NaOH 溶液，则所用两种NaOH 溶液的质量比为多少（1∶3）解：60% 60% 10% 1╲╱——30% ——╱╲20% 20% 30% 3五、用两种物质中同一元素的质量分数求两物质的质量比例6：FeO 中和FeBr2的混合物中Fe 的质量百分率为50%，求两物质的质量比（13∶15）解：FeO 7/9 13/54 13╲╱——1/2 ——╱╲FeBr27/27 5/18 15练习：1、实验室用密度为1.84 g·cm-398%的浓硫酸与密度为1.1 g·cm-3 15%的稀硫酸混和配制密度为1.4 g·cm-3 59%的硫酸溶液, 取浓、稀硫酸的体积比最接近的值是( )A、1:2B、2:1C、3:2D、2:32、实验测得乙烯与氧气混合气体的密度是氢气的14.5倍,可知其中乙烯的质量百分比为( )A、25.0%B、27.6%C、72.4%D、75.0%3、已知白磷和氧气可发生如下反应：P4 +3O2 = P4O6 ，P4 +5O2 = P4O10在某一密闭容器中加入62克白磷和50.4升氧气(标准状况), 使之恰好完全反应, 所得到的P4O10与P4O6的物质的量之比为( )A、1∶3B、3∶2C、3∶1D、1∶14、由CO 2、H 2和CO 组成的混合气在同温同压下与氮气的密度相同。

专题5·十字交叉法十字交叉法是快速求解二元混合问题的一种常见的有效方法．若a 1、a 2分别表示某二元混合物中的两种组分A 、B 的量，a 为a 1、a 2的加权．．平均值而非算术平均值，则n A /n B 为二元混合体系中的A 和B 的组成比．则：A a1a2－aa [ B a2a －a 1，二元混合物凡能满足下列关系的均可用以上方法．a 1·n A ＋a 2·n B ＝a (n A ＋n B ) 或a ＝BAB 2A1n n n a n a ＝a 1·BAA n n n ＋a 2·BAB n n n ＝a 1.A%＋a 2.B% (2)1.加权平均值和算术平均值有何区别？以上(2)中表示的均为加权平均值，其中A%＝BAA n n n ×100%，B%＝BAB n n n ×100%＝1－A%.A%、B% 即a 1、a 2在计算a 时所占的权重，a 为加权平均值．若为算术平均值，则a ＝2a a 21.显然，只有当A%＝B%＝50% 时，a ＝a ．一般是不相等的，a 不仅与a 1、a 2有关，更与各自在混合物中的权重．．有关．2.BA n n 表示什么量之比？不少学生滥用十字交叉法，但交叉出的BA n n 是什么量之比却模糊不清，有些不符合加权平均计算关系式的问题，乱用十字交叉法，势必导致错误结果．BA n n 表示什么量之比，要视参加交叉的a 1、a 2、a 的意义而定，a 1、a 2、a 的量纲中分母是何种物理量，BA n n 就是该物理量之比．在不同的情况，它可以是物质的量之比、气体体积之比、质量之比、原子个数比等．BAn n ＝12a aa a (1)(1)根据二元混合物的平均分子量，求两元的物质的量之比．若为气体也即体积之比．（此类情况最为熟悉，不再赘述）(2)根据只含2种同位素的元素的平均原子量，求两种同位素原子的个数比或物质的量之比或在自然界中的百分含量（也称作丰度）．为何直接求出的不是质量之比或体积之比呢？元素的平均原子量在数值上等于原子的平均摩尔质量，与平均分子量同理．M ＝BABB AA n n M n M n ＝M A ·A%＋MB ·B%.其中：n A /n B 的求法即可用十字交叉法． M A M B－MM M BM －MA BA n n 是何种物理量之比，只需找出M 的量纲，其分母为mol ，故BA n n 是物质的量之比，不可能为质量之比或原子的体积之比．1o若题目要求两种同位素原子的质量之比，可先用十字交叉法求出物质的量之比后，再分别乘以各原子的摩尔质量．BA m m ＝BB A A M n M n ＝BAA BM)MM(M )M M (2o 若提供的是两种同位素原子的质量分数A%、B%，要求元素的平均原子量，则可用如下列关系直接求解.M ＝总总n m ＝BAMB M A 100 g/mol例1、硼有两种天然同位素B 105、B 115，已知B 元素的原子量为10.80．下列对B 元素中B105的质量分数的判断正确的是（）Ａ.等于20% Ｂ.略大于20% Ｃ.略小于20% Ｄ.等于80%解①先求出物质的量之比B105 10 0.20BA n n ＝ABMMM M 41B115 11 0.80 B105的物质的量的分数为141×100%＝20%. B105的质量分数为115101×100%＜20%.答案：Ｃ．(3)同种溶质不同质量分数(A%、B%)的溶液混合而成质量分数为C%的溶液，求所取溶液的质量之比mA :mB . 根据混合前后溶质质量守恒，得m A ·A%＋m B ·B%＝(m A ＋m B )·C% 或 C%＝BA B A m m %B m %A m .该式满足十字交叉法加权平均关系A% (B－C)%C% B% (C－A)%注意：用十字交叉法求出只能是两种溶液质量的质量比，不能是体积之比．(4)根据两种有机物形成混合物的平均组成，来求两种有机物的物质的量之比．可选用平均C 原子数或平均H 原子数、平均O 原子数来求解．（此类情况在有机计算中已作叙述）．(5)有关反应热的问题例2、已知下列两个热化学方程式2H 2(g)＋O 2(g)＝2H 2O(l)＋571.6KJC 3H 8(g)＋5O 2(g)＝3CO 2(g)＋4H 2O(l)＋2220.0KJ. 实验测得H 2、C 3H 8混合气体共5mol 完全燃烧时放热3847KJ ，则原混合气体中H 2、C 3H 8的体积比是（）Ａ.1:3 Ｂ.3:1Ｃ.1:4Ｄ.1:1解析是求出每摩 H 2、C 3H 8完全燃烧时放出的热量，然后用十字交叉法求出．H 2 285.8 1450.6 769.4C 3H 8 2220.0 483.6 答案：Ｂ．BA m m ＝A C CB 832H C H n n ＝6.4836.1450≈13(6)结合有关反应的计算例3、有1.5L 的C 2H 4和C 2H 2组成的混合气体，恰好能与同条件下的 2.7L 的H 2完全加成生成乙烷，则原混合气体中C 2H 4、C 2H 2的体积比为（）Ａ.1:1 Ｂ.1:2Ｃ.1:4Ｄ.4:1解析每1LC 2H 4、C 2H 2分别加氢，消耗H 2的量为1L 、2L ，平均每1L 混合气体加H 2量为5.17.2＝1.8(L)，可用十字交叉法求解．C 2H 4 1 0.2 1.8 C 2H 2 2 0.8例4、 Li2CO 3和BaCO 3的混合物与盐酸完全反应，所消耗盐酸的量与等质量的CaCO 3和同浓度的盐酸反应所消耗盐酸的量相等．则混合粉末中Li 2CO 3和BaCO 3的质量之比为（）Ａ.3:5 Ｂ.5:3Ｃ.7:5 Ｄ.5:7解析首先请判断用下列十字交叉法求出两者之比是什么量之比．Li 2CO 3 74 97 100 ＝?BaCO 3 197 26若设均与 2 mol HCl 反应，则所需的Li 2CO 3、BaCO 3、CaCO 3各1 mol ，摩尔质量分别为74g/mol 、197g/mol 、100g/mol.故上面用十字交叉法求出的是Li 2CO 3和BaCO 3的物质的量之比．然后换算为质量比．332BaCO CO Li n n ＝2697332BaCO CO Li m m ＝197267497＝57.例5、Na 、Al 混合物0.2 mol 溶于足量盐酸，产生H 2 3.136mL(S.T.P)，求Na 、Al 的物质的量之比．解析Na ～21H 2Al ～23H 21mol21mol 1mol23mol2242H C H C V V ＝8.02.0＝412697混合金属～H0.2mol..mol1mol 0.7mol Na 0.5 0.8 0.7 Al 1.5 0.2..Na Aln n 例6、原计划实现全球卫星通讯需发射77颗卫星，这与铱(Ir)元素的原子核外电子数恰好相等,因此称为“铱星计划”。

3 .十字交叉法十字交叉法又名混合规则法、杠杆原理等，它在化学计算中具有能简洁和迅速求解的特点。

1、十字交叉法的数学原理：凡能列出一个二元一次方程组来求解的命题，均可用十字交叉法。

如: 1211221x x a x a x a +=⎧⎨+=⎩平12a a a -平a平21a a a -平结论：2121a a x x a a -=-平平十字交叉法立足于二元一次方程的求解过程，并把该过程抽象为十字交叉的形式，所以凡能列出一个二元一次方程来求解的命题均可用此法。

2、使用范围列表如下：⎧⎪⎨⎪⎩溶液度混合十字交叉法平均化式量（原子量）平均耗氧量3、注意事项（1）适用于十字交叉法的量必须是具有加权平均意义的量，具体说是一些分数，如：质量分时、体积分数、物质的量分数或者是一些具有复合单位的量，如：摩尔质量、密度、燃烧热等。

（2）物理量必须具有简单的加和性。

如溶液质量等，而溶液混合时的体积不具有加和性，所以一般不可用物质的量浓度交叉求两溶液的体积比，只有稀溶液混合时近似处理忽略体积．．．．．．．．变化．．才可用十字交叉法求解。

（3）比的问题：什么比——基准物质以什么物理量为前提进行分量和平均量的确定得出的比，以物质的量为前提得出的是基准物质的物质的量之比；以一定质量为前提得出的是基准物质的质量之比。

练习1、质量百分比浓度溶液的混合如用的98%浓硫酸与7%的稀硫酸混合配成20%的硫酸溶液，则需浓硫酸与稀硫酸以质量比为混合恰好配成20%的硫酸。

2、物质的量浓度溶液的混合如用18mol/L的浓硫酸与2mol/L的稀硫酸混合成6mol/L的硫酸，则浓硫酸与稀硫酸的体积比是。

3、相对原子量的求算铜有两种天然同位素6529Cu和6329Cu，已知通的相对原子质量为63.5，估算6529Cu的百分含量（丰度）约为A、5%B、25%C、50%D、75%4、平均相对分子质量的计算甲烷和氧气混合后，其平均相对分子质量为24，则混合气体中甲烷与氧气的体积比为。

十字交叉法的介绍十字交叉法可用于溶液浓度的计算，例如溶液的稀释、浓缩或混合等计算题。

使用此法，使解题过程简便、快速、正确。

下面通过例题介绍十字交叉法的原理。

同一物质的甲、乙两溶液的百分比浓度分别为a％、b％（a％＞b％），现用这两种溶液配制百分比浓度为c％的溶液。

问取这两种溶液的质量比应是多少？同一物质的溶液，配制前后溶质的质量相等，利用这一原理可列式求解。

设甲、乙两溶液各取m1、m2克，两溶液混合后的溶液质量是（m1 m2）。

列式m1a％ m2b％=（m1 m2）c％把此式整理得：m1m2=c-ba-c，m1m2就是所取甲、乙两溶液的质量比。

为了便于记忆和运算，若用C浓代替a，C稀代替b，C混代替C，m浓代替m1，m稀代替m2，把上式写成十字交叉法的一般形式，图示如下：图示中m浓m稀就是所求的甲、乙两溶液的质量比。

这种运算方法，叫十字交叉法。

在运用十字交叉法进行计算时要注意，斜找差数，横看结果。

十字交叉法的应用1．有关混合溶液的计算例1．现有20％和5％的两种盐酸溶液，若要配制600克15％的盐酸溶液，各需20％和5％的盐酸溶液多少克？分析与解：本题是用两种已知浓度的溶液来配制所需浓度的溶液，看似是求溶液的质量，实质是先求出两种浓度溶液的质量比，然后问题就迎刃而解。

用十字交叉法由图示可知，20％盐酸溶液与5％盐酸溶液的质量比应为2∶1∴20％盐酸溶液的质量600ⅹ23=400克5％盐酸溶液的质量600ⅹ13=200克2．有关改变溶剂质量的溶液浓度的计算例2．把20％的氯化钠溶液100克，加水稀释成浓度为4％的溶液，问需加水多少克？分析与解：本题是用水稀释改变溶液浓度的计算题，将水视为浓度为0％的溶液。

用十字交叉法由图示可知，20％氯化钠溶液与加入水的质量比应为m浓∶m水=4∶16=1∶4∴需加水的质量4ⅹ100=400克例3．现有200克浓度为10％的硝酸钾溶液，若要使其浓度变为20％，则需蒸发掉多少克水？分析与解：本题是蒸发水改变溶液浓度的计算题，将水视为浓度为0％的溶液。

高亖计算专题二差量法十字交叉法差量法是依据化学反响前后的某些〝差量〞〔固体质量差、溶液质量差、气体体积差、气体物质的量之差等〕与反响或生成物的变化量成正比而树立的一种解题方法。

此法将〝差量〞看作化学方程式右端的一项，将差量〔实践差量〕与化学方程式中的对应差量〔实际差量〕列成比例，其他解题步骤与按化学方程式列比例或解题完全一样。

〔一〕质量差法【例题1】在1升2摩/升的稀硝酸溶液中参与一定量的铜粉，充沛反响后溶液的质量添加了13.2克，问：〔1〕参与的铜粉是多少克？〔2〕实际上可发生NO气体多少升？〔规范状况〕【剖析】硝酸是过量的，不能用硝酸的量来求解。

铜跟硝酸反响后溶液增重，缘由是生成了硝酸铜，所以可应用这个变化停止求解。

3Cu + 8HNO3 = 3Cu(NO3)2 + 2NO↑+ 4H2O 增重192 44.8 636-504=132X克Y升13.2 可得X=19.2克，Y=4.48升【练习】1.在天平两盘内各放有等质量等体积的烧杯，区分盛有同物质的量同体积的盐酸，天平平衡。

再区分加人一定量的镁、铝，充沛反响后，假定使天平依然坚持平衡，那么加人镁、铝的物质的量之比为〔〕〔A〕9：8 〔B〕11：12 〔C〕12：11 〔D〕3：42.将4.6g钠和4.8g镁区分投入盛有等物质的量浓度、等体积的稀硫酸的两个烧杯中，充沛反响后，所得溶液总质量区分为mg和ng，那么不能够的关系为〔〕〔A〕m=n 〔B〕m>n 〔C〕m<n 〔D〕m≤n〔二〕体积差法【例题2】10毫升某气态烃在80毫升氧气中完全熄灭后，恢复到原来状况〔1.01×105Pa , 270C〕时，测得气体体积为70毫升，求此烃的分子式。

【剖析】原混和气体总体积为90毫升，反响后为70毫升，体积增加了20毫升。

剩余气体应该是生成的二氧化碳和过量的氧气，下面可以应用烃的熄灭通式停止有关计算。

C x H y + 〔x+y/4〕O2→xCO2 + y/2 H2O 体积增加11+y/410 20计算可得y=4 ，烃的分子式为C3H4或C2H4或CH4【练习】某体积可变的密闭容器，盛过量A和B的混合气体，在一定条件下发作反响；A ＋3B≒2C，假定维持温度和压强不变，当到达平衡时，容器的体积为VL，其中C气体的体积占10％，以下推断正确的选项是〔〕①原混和气体的为l.2L ②原混合气体的体积为1.1L③反响达平衡时气体A消耗掉0.05VL ④反响达平衡时气体B消耗掉0.05VL〔A〕②③〔B〕②④〔C〕①③〔D〕①④〔三〕物质的量差法【例题3】白色固体PCl5受热即挥发并发作分解：PCl5〔气〕= PCl3〔气〕+ Cl2现将5.84克PCl5装入2.05升真空密闭容器中，在2770C到达平衡时，容器内的压强为1.01×105Pa ，经计算可知平衡时容器内混和气体物质的量为0.05摩，求平衡时PCl5的分解百分率。

化学计算中“十字交叉法”的数学原理和应用一. “十字交叉法”简介“十字交叉法”是二元混合物（或组成）计算中的一种特殊方法，若已知两组分量和这两个量的平均值，求这两个量的比例关系等，多可运用“十字交叉法”计算。

十字交叉法在化学计算中是一种常用的方法，在很多习题中采用十字交叉法可以简化计算过程，提高计算效率。

下面先从一道简单的例题来介绍何为十字交叉法。

例1、50克10%的硫酸溶液和150克30%的硫酸溶液混合后，所得硫酸溶液的质量分数是多少？采用十字交叉法计算的格式如下：设混合后溶液的质量分数为x%，则可列出如下十字交叉形式所得的等式：10%的溶液 10 30 — xX =30%的溶液 30 x — 10由此可得出 x = 25，即混合后溶液的质量分数为25%。

以上习题的计算过程中有一个十字交叉的形式，因此通常将这种方法叫做“十字交叉法”。

然而怎样的计算习题可以采用这种方法？且在用“十字交叉法”时，会涉及到最后差值的比等于什么的问题，即交叉后所得的差值之比是实际中的质量之比还是物质的量之比？这些问题如果不明确，计算中便会得出错误的结论。

针对以上问题，在以前的教学中，可能往往让学生从具体的习题类型死记差值之比的实际意义。

由于十字交叉法常用于：①核素“丰度”与元素相对原子质量的计算；②混合气体不同组分体积之比和混合气体平均相对分子质量的计算；③不同浓度的同种溶液混合后质量分数与组分溶液质量之比的计算等类型的习题中。

因此可以简单记忆为前两种类型中，差值之比为物质的量之比，第三种类型差值之比为质量之比。

这种记忆方法束缚了学生的思维，同时也限制了“十字交叉法”的使用范围。

实质上“十字交叉法”的运用范围很广，绝不仅仅只能在以上三种类型的习题中才可运用。

然而不同情况下，交叉后所得的差值之比的实际意义是什么？该怎样确定其实际意义？是我们应该探讨和明了的问题。

要解决此问题，就要明了“十字交叉法”的数学原理，然后再从原理的角度去分析，便能确定差值之比在何时为组分的质量之比，何时为组分的物质的量之比。

高中化学的十字相乘法十字交叉法又称图解法，应用于二元混合体系所产生的具有平均意义的计算问题，表现出实用性强，能准确、简便、迅速求解的特点。

适用范围：“十字交叉法”适用于两组分混合物（或多组分混合物，但其中若干种有确定的物质的量比，因而可以看做两组分的混合物），求算混合物中关于组分的某个化学量（微粒数、质量、气体体积等）的比值或百分含量。

例1：实验测得乙烯与氧气的混合气体的密度是氢气的14.5倍。

可知其中乙烯的质量分数为（ ）A.25.0%B.27.6%C.72.4%D.75.0%解析：要求混合气中乙烯的质量分数可通过十字交叉法先求出乙烯与氧气的物质的量之比（当然也可以求两组分的质量比，但较繁，不可取），再进一步求出质量分数。

这样，乙烯的质量分数是：ω（C 2H 4）=321283283⨯+⨯⨯×100％=72.4% 答案：C 。

（解毕）二、十字交叉法的解法探讨：1.十字交叉法的依据：对一个二元混合体系，可建立一个特性方程： ax+b(1－x)=c(a 、b 、c 为常数，分别表示A 组分、B 组分和混合体系的某种平均化学量，如：单位为g/mol 的摩尔质量、单位为g/g 的质量分数等) ；x 为组分A 在混合体系中某化学量的百分数（下同）。

如欲求x/(1－x)之比值，可展开上述关系式，并整理得： ax －bx=c －b解之，得： ba c a xb a bc x --=---=1, 即：ca b c x x --=-1 2.十字交叉法的常见形式：为方便操作和应用，采用模仿数学因式分解中的十字交叉法，记为：3.解法关健和难点所在：十字交叉法应用于解题快速简捷，一旦教给了学生，学生往往爱用，但是也往往出错。

究其原因，无外乎乱用平均量（即上述a 、b 、c 不知何物）、交叉相减后其差值之比不知为何量之比。

关于上述a 、b 、c 这些化学平均量，在这里是指其量纲为（化学量1 ÷化学量2）的一些比值，如摩尔质量（g/mol ）、溶液中溶质的质量分数(溶质质量÷溶液质量)或关于物质组成、变化的其它化学量等等。

高中化学二元混合物的十字交叉法解法速解的前提：1、必须清楚“十字交叉法”运用后的比例比系——“看分母”法则。

即特性数值的分母所表示的物理量之比。

因为对于二元混合物而言，设x 1、x 2是混合物两组分的某化学量，α 1、α 2为两组分的特性数值，ā为混合物的特性数值，若满足方程式α 1x 1+α 2x 2== ā(x 1 + x 2)可知 x 1（α 1- ā） == x 2（ā-α 2）即 x 1/x 2 ==（ā-α 2）/（α 1- ā）。

凡满足上述方程式的化学量的求解都不得可以用特性数值的“十字交叉法”形式来表示：2、必须清楚“十字交叉法”的适用范围现举几例，若按常规方法解二元一次方程，虽好理解，但费时且麻烦，若能正确运用“十字交叉法”，便可方便、迅速、准确地解题。

例1 现有100克碳酸锂和碳酸钡的混和物，它们和一定浓度的盐酸反应时所消耗盐酸跟100克碳酸钙和该浓度盐酸反应时消耗盐酸量相同。

计算混和物中碳酸锂和碳酸钡的物质的量之比。

分析可将碳酸钙的式量理解为碳酸锂和碳酸钡的混和物的平均式量，利用十字交叉法计算可有：所以，碳酸锂和碳酸钡的物质的量之比为97∶26。

例2 天然的和绝大部分人工制造的晶体都存在各种缺陷。

例如在某种NiO晶体中就存在如右图所示的缺陷：1Ni 2+个空缺，另有2个Ni 3+取代，其结果晶体仍呈电中性，但化合物中Ni原子和O原子的比值却发生了变化。

该氧化镍样品组成为Ni 0.97O，试计算该晶体中的Ni 3+和Ni 2+的离子个数比。

分析本题所求的是Ni 3+和Ni 2+的离子个数比，所以我们所选的特性数值的分母必须是Ni 3+和Ni 2+的离子个数。

由此可知：所以，例3 某亚硫酸钠已部分被氧化成硫酸钠，经测定混合物中的质量分数为25%，求该混合物中亚硫酸钠与硫酸钠的物质的量之比。

分析本题目传统解法是解二元一次方程，但需要假设一些数据，比较费时，但如正确运用“十字交叉法”，弄清比例关系，则能很快地解决问题根据前面介绍的“看分母”法则可知计算出的比例是亚硫酸亚铁钠与硫酸钠中所含硫元素的质量比，但因是同种元素，且每个分子中均含1个硫原子，所以硫的质量比即等于其物质的量之比，所以二者物质的量之比为7∶1。

高中化学计算题常用技巧：十字交叉法导语：“未来的文盲不再是不识字的人，而是没有学会怎样学习的人。

”科学的学习方法就是我们打开知识宝库的金钥匙。

如果我们掌握了科学的学习，也就具备了获取知识的能力，将让我们终身受益。

在化学中凡可按a1x1+a2x2=ā(x1+x2)或(a1-ā)/(ā-a2)=x2/x1计算的问题，都可以应用“十字交叉法”计算。

“十字交叉法”是化学计算中广泛使用的解题方法之一，它具有形象，直观的特点。

如何计算呢?首先应先写出混合两组分对应的量a1 、a2 和交叉点的平均值ā，然后按斜线作差取绝对值即得出相应物质的配比关系，其“十字交叉法”为：组分1： a1 ā-a2 x1 x1为组分分数ā—―= —组分2： a2 a1-ā x2 x2为组分分数“十字交叉法”适用的范围是：凡是具有均一性、加和性的混合物，都可运用这种方法进行计算，但须注意，计算所得比值是质量比还是物质的量比，下面介绍几种常见“十字交叉法”的计算：一、质量分数“十字交叉法”混合物中某元素原子或原子团质量守恒，且具有加和性，所以可用“十字交叉法”求混合物中某元素或某物质的质量分数。

例3：含氯54.2%的氯化钠和氯化钾的混合物，其中含NaCl的质量分数是( )A、50%B、35%C、75%D、60%解析：设氯化钠质量是m1、氯化钾质量是m2，依据氯元素守恒，则有60.7%m1+47.7%m2=54.2%(m1+m2),所以可用“十字交叉法”求解NaCl：60.7 6.5 1 m 154.2 —– = —KCl： 47.7 6.5 1 m2所以w(NaCl)=6.5/(6.5+6.5) ×100%=50%二、浓度“十字交叉法”溶液在稀释或浓缩时溶质的量守恒，如溶液浓度为质量分数有：m1a%+m2b%=(m1+m2)c%，或溶液浓度为物质的量浓度有：C1V1+C2V2=(V1+V2)C(稀溶液)，所以混合溶液浓度的计算可以用“十字交叉法”。