实验四核衰变的统计规律与放射性测定的实验数据处理

实验二 核衰变的统计规律实验人：*** 合作者：*** 实验时间：2011/06/03一、引言对核衰变产生的射线可用计数方式测量。

然而多次测量相同时间间隔内的计数，即使保持相同的实验条件，每次测量的结果并不相同，而是围绕某一平均值上下涨落，反映出核衰变的随机性二、实验目的1、了解并验证原子核衰变及放射性计数的统计性2、了解统计误差的意义，掌握计算统计误差的方法3、学习检验测量数据的分布类型的方法三．原理1．放射性测量的随机性和统计性在做重复的放射性测量中，即使保持完全相同的实验条件（例如放射性的半衰期足够长，因此在实验时间内可以认为其强度基本上没有变化；源与计数器的相对位置始终保持不变；每次测量时间不变；测量仪器足够精确，不会产生其它的附加误差等等），每次的测量结果并不完全相同，而是围绕其平均值上下涨落，有时甚至有很大的差别，也就是说物理实验的测量结果具有偶然性，或者说随机性。

物理测量的随机性产生原因不仅在于测量时的偶然误差，而且更是物理现象(当然包括放射性核衰变)本身的随机性质，即——物理量的实际数值时刻围绕着平均值发生微小起伏。

在微观现象领域，特别是在高能物理实验中，物理现象本身的统计性更为突出。

按照量子力学的原理，对处于同一个态的微观粒子，测量同一个可观测的物理量时，即使不存在任何测量误差，各次测量结果也会不同，除非粒子处于这个可观测量的本征态；比如同一种粒子的寿命，其实测值分布在从相当短到相当长的范围内。

另一方面，所谓偶然的东西，是一种有必然性隐藏在里面的形式；我们正是要通过研究其统计分布规律从而找出在随机数据中包含的规律性。

2．核衰变数的统计分布放射性原子核衰变数的统计分布可以根据数理统计分布的理论来推导。

放射性原子核衰变的过程是一个相互独立彼此无关的过程，即每一个原子核的衰变是完全独立的，与其他原子核是否衰变无关；因此放射性原子核衰变的测量计数可以看成是一种伯努里试验问题。

在N 0个原子核的体系中，单位时间内对于每个原子核来说只有两种可能：A 类是原子核发生衰变，B 类是没有发生核衰变。

G-M特性及核衰变统计规律实验目的1.了解G-M计数器的工作原理，有关特性及使用方法。

2.以G-M计数器为探测设备，验证核衰变的统计规律。

3.了解统计误差的意义，掌握计算统计误差的方法。

实验内容1.在一定甄别阈值下，测量G-M计数管的坪曲线，确定坪曲线的各个参量，并确定其工作电压。

2.用示波器测定计数装置的分辨时间。

3.观察G-M计数管的工作电压与输出脉冲幅度的关系。

4.在相同条件下，对某放射源进行重复测量，画出放射性计数的频率直方图，并与理论正态分布曲线作比较。

5.在相同条件下，对本底进行重复测量，画出本底计数的频率分布图，并与理论泊松分布作比较。

实验原理1G-M计数管1.1G-M管的结构和工作原理G-M计数管是一种气体探测器，结构类型很多，最常见的有圆柱形和钟罩形两种，它们都是由同轴圆柱形电极构成。

图1是其结构示意图，中心的金属丝为阳极，管内壁圆筒状的金属套（或一层金属粉末）为阴极，管内充有一定量的混合气体（通常为惰性气体及少量的猝灭气体），钟罩形的入射窗在管底部，一般用薄的云母片做成；圆柱形的入射窗就是玻璃管壁。

测量时，根据射线的性质和测量环境来确定选择哪种类型的管子。

对于α和β等穿透力弱的射线，用薄窗的管子来探测；对于穿透力较强的γ射线，一般可用圆柱型计数管。

G-M 管工作时，阳极上的直流高压由高压电源供给，于是在计数管内形成一个柱状对称电场。

带电粒子进入计数管，与管内气体分子发生碰撞，使气体分子电离即初电离（γ粒子不能直接使气体分子电离，但它在阴极上打出的光电子可使气体分子发生电离）。

初电离产生的电子在电场的加速下向阳极运动，同时获得能量，当能量增加到一定值时，又可使气体分子电离产生新的离子对，这些新离子对中的电子又在电场中被加速再次发生电离碰撞而产生更多的离子对。

由于阳极附近很小区域内电场最强，则此区间内发生电离碰撞几率最大，从而倍增出大量的电子和正离子，这个现象称为雪崩。

雪崩产生的大量电子很快被阳极收集，而正离子由于质量大、运动速度慢，便在阳极周围形成一层“正离子鞘”，阳极附近的电场随着正离子鞘的形成而逐渐减弱，使雪崩放电停止。

第一部分G-M计数器【实验目的】1、了解G_M计数器的工作原理，掌握其基本性能及测试方法。

2、学会正确使用G-M计数器的方法。

3、了解探测器输出信号与输出回路参数的关系，学会正确选择G-M计数器系统输出回路参数。

【实验内容】1.在一定的甄别阈下，测量卤素G-M管的坪曲线，确定这些坪曲线的各个参数并选择工作电压。

2.用示波器测定G-M计数器的分辨时间。

3.观察并记录G-M管的输出电流、电压脉冲与工作电压及输出回路参数的关系。

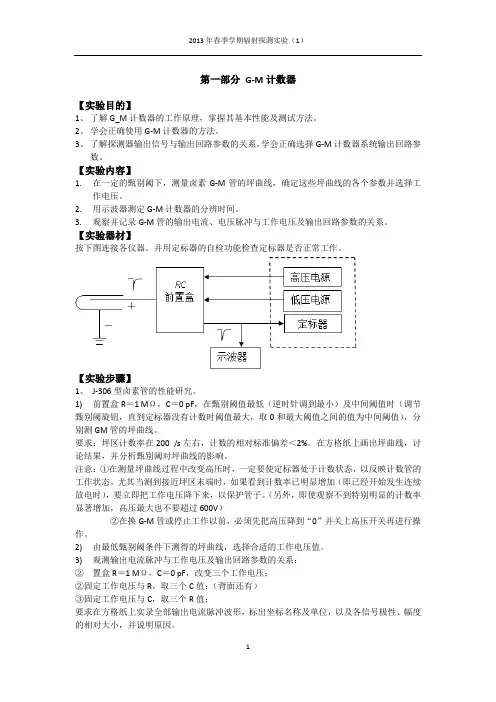
【实验器材】按下图连接各仪器。

并用定标器的自检功能检查定标器是否正常工作。

【实验步骤】1、J-306型卤素管的性能研究。

1) 前置盒R＝1 MΩ，C＝0 pF，在甄别阈值最低（逆时针调到最小）及中间阈值时（调节甄别阈旋钮，直到定标器没有计数时阈值最大，取0和最大阈值之间的值为中间阈值），分别测GM管的坪曲线。

要求：坪区计数率在200 /s左右，计数的相对标准偏差＜2%。

在方格纸上画出坪曲线，讨论结果，并分析甄别阈对坪曲线的影响。

注意：①在测量坪曲线过程中改变高压时，一定要使定标器处于计数状态，以反映计数管的工作状态。

尤其当测到接近坪区末端时，如果看到计数率已明显增加（即已经开始发生连续放电时），要立即把工作电压降下来，以保护管子。

（另外，即使观察不到特别明显的计数率显著增加，高压最大也不要超过600V）②在换G-M管或停止工作以前，必须先把高压降到“0”并关上高压开关再进行操作。

2) 由最低甄别阈条件下测得的坪曲线，选择合适的工作电压值。

3) 观测输出电流脉冲与工作电压及输出回路参数的关系：②置盒R＝1 MΩ，C＝0 pF，改变三个工作电压；②固定工作电压与R，取三个C值；（背面还有）③固定工作电压与C，取三个R值；要求在方格纸上实录全部输出电流脉冲波形，标出坐标名称及单位，以及各信号极性、幅度的相对大小，并说明原因。

注意：①中的三个电压值必须在坪区范围内；为观察到形状较好的电流和电压波形，②、③及以下各步骤中的工作电压可比步骤(2)中选择的工作电压低，具体数值可以取R ＝1 M Ω，C ＝0 pF 时，示波器观察电流或电压波形不出现饱和的最大工作电压值。

盖革-弥勒计数器及核衰变的统计规律盖革-弥勒计数器是气体探测器的一种，用來测定射线强度，既单位时间的粒子个数。

近年 来，随着闪烁探测器及半导体探测器的发展，其重耍性有所下降，但由于它的没备简单，使 用方便，在有关的放射性测撒屮仍在广泛使用。

一、 实验目的掌握G-M 计数器的工作难础，测定其有关特性，学会使用；以G-M 计数器米测试设备，验 证核袞变的统计规律；学会使川放射性测3结果的误差表示法，学会多次测呈结果的误差计 算及测试吋间的选择。

二、 实验原理1、G-M 计数器原理：G-M 计数器是利用射线使计数管内的丁.作气体电离，然后收集产生的电荷来记录射线的 探测器。

玻璃管内冇糾筒状阴极，在明极对称轴上.装冇丝状阳极。

先将管内抽成真空，冉充入一定s 的惰性气体和少量猝灭气体（卤素或奋机物）在G-M 计数管两级加上电压，没其阳极半 径为a ，阴极半径为b ，阳极与叨极间的电压为U ，则沿着管径向位置为r 处的电场强度 为 ，可见随着r 减小，电场强度增大，且阳极附近急剧增大。

2、脉冲原理（丨）当射线进入G-M 管中使得管中气体电离后，正离子和负离子在管内电场的作川下分 别14阴极和阳极移动。

在阳极附近强人的电场作川K,电子获得强人的动能以至于将阳极附 近的气体电离。

经过多次碰撞，殃及附近的电子急剧增多，形成了 “雪劢电子”；在这些碰 撞中会产生大S 的紫外线光了，这些光了能进一步的产生第二波的“雪崩”效应，增加电了。

这个电子不断培加的过程称为气体放大。

（2） 雪崩过程发屮在殃及附近，加上电子的质量远远小于阳离子的质量，速度比阳离子快， W 此电子很快被阳极吸收，在管内留下一个被大量HI 离子构成的叩离子鞘包围着的叩极。

正 离子鞘将随着电离的发生逐渐增厚，由于正离子鞘的作用，阳极附近的电场将随之减小，以 致新电子无法增殖，即电场强度不足以引发雪崩效应，雪崩效座停止，正离子鞘停止生成， 放电便终止了，何候，正离子鞘在屯场的作用下慢慢移向阴极，最后到达阴极被中和，阳极 附近的电场也随之恢复，使得与G-M 串联的电阻记录下一个电压脉冲。

实验一核衰变与放射性计数的统计规律第一部分 G-M计数器一.实验目的1、了解G-M管的工作原理，掌握其基本性能及其测试方法。

2、学会正确使用G-M管计数装置的方法。

3、了解探测器输出信号与输出回路参数的关系，学会正确选择G-M管计数系统输出回路参量。

二.实验内容1、在一定的甄别阈下，测量卤素G-M管的坪曲线，确定这些坪曲线的各个参量并选择工作电压。

2、用示波器观察法和双源法测定卤素G-M管计数装置的分辨时间。

3、观察并记录G-M计数管的输出电流、电压脉冲与工作电压及输出回路参数的关系。

三.实验原理1、G-M管是一种气体探测器。

当带电粒子射入其灵敏体积时，引起气体原子电离。

电离产生的电子在阳极丝附近的强电场中又引起一系列碰撞电离，即触发“自持放电”。

这一过程产生的电子和正离子向两极漂移时，在外回路产生脉冲信号。

2、从G-M管的工作机制可以看出，入射带电粒子仅仅起一个触发放电的作用，G-M管的输出电流、电压信号的幅度与形状和入射粒子种类与能量无关，只和计数管的几何参量、工作电压以及输出回路参量有关。

在G-M管的使用中，坪特性是其最重要的性能之一。

坪特性是判断管子好坏的主要依据，也是选择管子工作电压的依据。

坪特性曲线就是在一定的实验条件下当入射粒子的注量率不变时，计数管的计数率随工作电压变化的曲线，见图1－1。

图1-1 G-M计数管的坪曲线表征坪特性的参量主要有：起始电压(Vs)：即计数管开始计数时的电压。

坪长： B A =V -V 坪长（单位：百伏） （1-1） 这是管子的工作区域，工作电压一般可选在坪区的21~31的范围内。

坪斜：()100% ()2B A B A B A n n n n V V -=⨯+-坪斜（单位：％/百伏） （1-2） 坪斜主要是由假计数引起的，当然它的值越小越好。

当工作电压高于B V 时，曲线急剧上升，表明管子内发生了持续放电，这会大大缩短管子的寿命，因此在使用中必须注意避免这种情况。

核能实验测量放射性衰变的速率核能实验是一项重要的研究领域，涉及到粒子物理学和核物理学等多个学科的知识。

在这个领域中，测量放射性衰变的速率是非常重要的一项实验。

本文将介绍核能实验中如何准确测量放射性衰变的速率，并探讨其在科学研究和实际应用中的意义。

一、放射性衰变的概念与特点放射性衰变是指不稳定原子核自发地发射粒子或光子，转变为其他物质的过程。

这个过程是随机的，每个原子核在单位时间内发生衰变的概率是相同的。

放射性衰变速率是指单位时间内发生的衰变事件数。

二、测量放射性衰变的速率的方法在核能实验中，有多种方法可以测量放射性衰变的速率。

其中，最常用的方法是计数法。

计数法是通过测量单位时间内发生的衰变事件数来确定放射性衰变速率的方法。

实验者使用一个放射性样品，并利用探测器对其辐射进行测量。

根据在给定时间内探测到的衰变事件数，可以计算出放射性衰变速率。

为了减小误差，实验者需要控制实验环境的背景辐射，并对数据进行统计处理。

此外，为了提高测量的准确性，多次测量可以取得更可靠的结果。

三、放射性衰变速率的应用测量放射性衰变速率在核能实验中有着广泛的应用。

首先，通过测量放射性元素的衰变速率，可以确定其半衰期，即元素衰变到其初始数目的一半所需的时间。

这对于核能研究以及地质学和考古学等领域的年代测定具有重要意义。

其次，测量放射性衰变速率还可用于辐射治疗和核能安全监测等方面。

在辐射治疗中，通过精确测量患者体内放射性药物的衰变速率，可以确定治疗剂量并监测治疗效果。

在核能安全监测方面，测量放射性核素的衰变速率可用于监测环境中的辐射水平，以保障公众的健康与安全。

四、放射性衰变速率测量的局限性与挑战尽管放射性衰变速率测量方法已经相当成熟，但仍然存在一定的局限性与挑战。

首先，放射性样品的选择和制备需要谨慎考虑，以保证实验的准确性。

其次，环境背景辐射对测量结果有较大影响，实验者需要采取适当的措施进行背景辐射的补偿和剔除。

此外，放射性样品的安全处理以及对实验者的辐射防护也是一个重要问题。

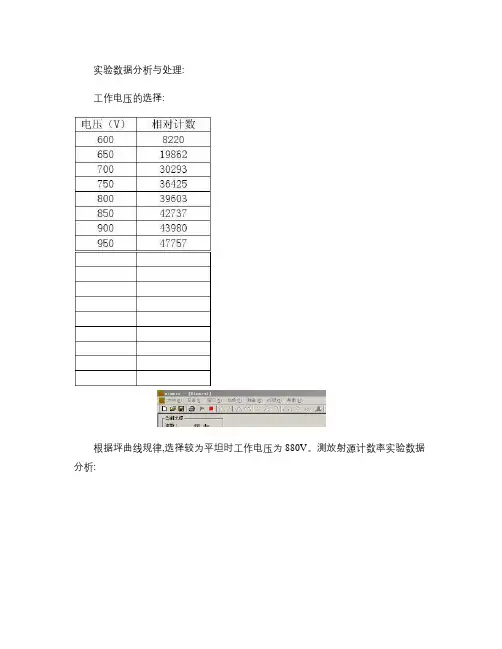
实验数据分析与处理:工作电压的选择:根据坪曲线规律,选择较为平坦时工作电压为880V。

测放射源计数率实验数据分析:实验分析:1. 探测器与放射源的几何位置应保持合理(两者不宜离开太远2.实验中要保证不触碰探测仪,因为本实验是一种强度测量,所以一切有可能影响探测器探测效率的因素都必须严格保持不变,如工作点要保持稳定探测器和源的几何位置也不可以改变。

3.实验数据分析时,软件曾出现提示框显示:“已超出正态分布范围,无法分析”的字样。

打开实验数据后发现实验的第一个数据与之后的数据相去甚远(后面数据均维持在3300~3500范围内,第一个数据为20000+的值,在去除第一个数据后分析实验,软件得以成功分析。

可能由于电压值发生一定变化导致第一个数据出现一定问题,须删除无效数据后进行数据处理。

思考题1.什么是坪曲线?谈谈坪曲线的测量在研究核衰变统计规律实验中的意义? 答:坪曲线是入射粒子的强度不变时,计数器的计数率随工作电压变化的曲线。

测定坪曲线是为了选择一个合适的工作电压,以减少电压漂移对实验的影响.工作点若选在坪区,即使仪器和探头的性能都有变化,也可使总计数率保持稳定。

所以应在曲线较平的部分以及源计数率高本底计数率相对较低处选择工作电压。

2.什么是放射性核衰变的统计性?它服从什么规律?答:放射性原子核衰变的过程是一个相互独立彼此无关的过程,即每一个原子核的衰变是完全独立的,与其他原子核是否衰变无关;因此放射性原子核衰变的测量计数可以看成是一种伯努里试验问题。

其统计分布满足一定的规律性,称此规律性为核衰变的统计性,它服从正态分布。

3.σ的物理意义是什么?以单次测量值N 来表示测量值时,为什么是N N ±?其物理意义又是什么?答:σ的物理意义是在相同条件下作重复测量时,每次测量结果围绕着平均计数值的一个涨落大小。

在实际运算中由于出现概率较大的计数值与平均值N 的偏差不大,我们可以用N 来代N ;因此对于单次测量值N ,可以近似地说在N N ±范围内包含真值的概率是68.3%,这样一来用单次测量值就大体上确定了真值的范围。

实验10-2 核衰变的统计规律【实验目的】1．测量NaI(Tl)闪烁探测器的坪曲线，确定合适的工作电压；指导：用闪烁探测器测量强度不变的放射源时，改变光电倍增管的高压，计数率也会随之改变；原因在于任何一种射线在闪烁探测器中产生的脉冲幅度都不会完全一样，输出脉冲的幅度也分布在一定范围内。

尽管如此，只要射线的能量不是特别低而探测器的工作状态又选择得当，绝大部分信号脉冲都会比光电倍增管的噪声脉冲大。

当电压足够高，信号脉冲幅度基本上都超过了仪器的甄别阈而绝大部分噪声的幅度又还比甄别阈小很多时，随着高压的增加计数率的增加就很缓慢了，这时就出现了“坪区”。

在实验中，重要的是向学生说明在许多核物理实验中测量坪曲线的意义何在。

在本实验中，由于高压相对比较稳定，因此我们在实践中发现选取坪曲线较为平坦（计数率随高压漂移变化较小）的工作点和坪曲线较为陡峭的工作点两者的差异不大。

2．了解并验证原子核衰变及放射性计数的统计性；指导：本实验通过反复测量放射源（137Cs 或60Co ）在一段时间内强度并作为一个随机事件，取一个样本容量为A 的样本来观察其结果是否符合正态分布。

当然，源的强度本身随时间衰减，但137Cs 的半衰期长达30年，可以近似认为在实验时间内（大约1——2小时）源强不变。

3．了解统计误差的意义，掌握计算统计误差的方法；指导：这一实验需要一定的概率论和数理统计方面的基础，比如二项式分布、泊松分布、正态分布以及样本均值、样本方差、样本方差的无偏估计；学生应该已经学习过相关课程，若没有接受过类似训练，实验讲义的原理部分已经列出了所需知识。

需要说明的是： 鉴于A x x Ai i /)(12∑=-不是方差2S 的无偏估计，)1/()(12--∑=A x x Ai i 才是，因此取)1/()(12--=∑=A x x S Ai ix 作为样本标准差的无偏估计。

（参见任一概率论数理统计教材） 4．学习检验测量数据的分布类型的方法。

实验一核衰变与放射性计数的统计规律实验报告第一部分G-M计数器一.实验目的1、了解G-M管的工作原理，掌握其基本性能及其测试方法。

2、学会正确使用G-M管计数装置的方法。

3、了解探测器输出信号与输出回路参数的关系，学会正确选择G-M管计数系统输出回路参量。

二.实验内容1、在一定的甄别阈下，测量卤素G-M管的坪曲线，确定这些坪曲线的各个参量并选择工作电压。

2、用示波器观察法和双源法测定卤素G-M管计数装置的分辨时间。

3、观察并记录G-M计数管的输出电流、电压脉冲与工作电压及输出回路参数的关系。

三.实验原理1、G-M管是一种气体探测器。

当带电粒子射入其灵敏体积时，引起气体原子电离。

电离产生的电子在阳极丝附近的强电场中又引起一系列碰撞电离，即触发“自持放电”。

这一过程产生的电子和正离子向两极漂移时，在外回路产生脉冲信号。

2、从G-M管的工作机制可以看出，入射带电粒子仅仅起一个触发放电的作用，G-M管的输出电流、电压信号的幅度与形状和入射粒子种类与能量无关，只和计数管的几何参量、工作电压以及输出回路参量有关。

在G-M管的使用中，坪特性是其最重要的性能之一。

坪特性是判断管子好坏的主要依据，也是选择管子工作电压的依据。

坪特性曲线就是在一定的实验条件下当入射粒子的注量率不变时，计数管的计数率随工作电压变化的曲线，见图1－1。

图1-1 G-M计数管的坪曲线表征坪特性的参量主要有：起始电压(Vs)：即计数管开始计数时的电压。

坪长： B A =V -V 坪长（单位：百伏）（1-1） 这是管子的工作区域，工作电压一般可选在坪区的21~31的范围内。

坪斜：()100% ()2B A B A B A n n n n V V -=⨯+-坪斜（单位：％/百伏） （1-2）坪斜主要是由假计数引起的，当然它的值越小越好。

当工作电压高于B V 时，曲线急剧上升，表明管子内发生了持续放电，这会大大缩短管子的寿命，因此在使用中必须注意避免这种情况。

放射性衰变的实验观察与分析实验观察与分析：放射性衰变放射性衰变是指一种原子核自发地发射出射线，从而转变成另一种元素或同位素的现象。

在这个实验中，我们对一种放射性物质的衰变进行了观察与分析。

实验设备与材料：1. 放射性样品（已知是铀）2. 探测器3. 电子计数器4. 实验记录表格实验步骤：1. 将放射性样品放置在探测器旁边，并将探测器连接到电子计数器上。

2. 开始记录计数器每隔一段时间（比如5分钟）所测得的粒子数目，并将其填写在实验记录表格中。

观察与结果：在实验过程中，我们观察到计数器每隔一段时间就会记录到一定数量的粒子。

最初的数目较多，随着时间的推移，记录到的粒子数目逐渐减少，但并未完全消失。

这是因为放射性衰变是一个随机的过程，每个原子核发生衰变的概率是相同的，但时间上的分布是不确定的。

根据粒子数目的变化曲线，我们可以看到一些规律。

一开始，衰变速率很快，数目下降得很快。

但随着时间的推移，衰变速率逐渐减慢，说明衰变速率是逐渐减小的。

这是因为随着原子核数量的减少，相互碰撞的概率也减小，从而导致衰变速率的减缓。

然而，即使在很长时间之后，仍然会记录到一些粒子，这说明放射性衰变是一个持久的过程，不会完全停止。

分析与讨论：根据实验结果，我们可以通过衰变速率的变化来推断放射性物质的半衰期。

半衰期是指在一半的放射性原子核衰变所需的时间。

通过观察衰变速率逐渐减慢的趋势，我们可以估算出半衰期的大致大小。

此外，还可以通过观察放射性衰变产生的射线类型来进一步确认放射性物质的性质。

射线的类型包括阿尔法粒子（α粒子）、贝塔粒子（β粒子）和伽马射线（γ射线）。

通过分析这些射线的能量和穿透能力，可以确定放射性物质的具体类型和原子核的结构。

需要注意的是，放射性衰变是一个存在一定风险的实验。

对于放射性物质的处理和测量需要符合安全操作规程，并使用适当的防护设备。

总结：通过对放射性衰变的实验观察与分析，我们可以了解放射性物质的特性，并且可以通过衰变速率的变化推断出物质的半衰期。

所谓“雪崩”电子；在这些碰撞中会产生大量紫外线光子, 这些光子能够进一步地近代物理实验实验报告盖革-弥勒计数器及核衰变的统计规律同组者：****操作人员：*** .号. *******一.实验仪器:G-M 计数器，3粒子放射源，脉冲示波器。

二•实验原理:1. G-M 计数器原理:高压电源定量惰性气体和少量猝灭气体（卤素或有机物）在G-M 阳极半径为a ，阴极半径为b ，则沿着管径向位置为r 处的电场强度为E=V 。

见随着r 减小，电场强度增大，且在阳极附近急剧增大。

2. 脉冲原理:1. ）当射线进入G-M 管中使得管中气体电离后，正离子和负离子在管内电场的作用下分别向阴极和阳极移动。

在阳极附近强大的电场作用下，电子获得极大的动能定标器G-M 计数管玻璃管内有圆筒状阴极， 在阴极对称轴上装有丝状阳极。

先将管内抽成真空,再冲入一计数管两极加上电压/In(a/b)可以至于将阳极附近的气体电离。

经过多次碰撞，阳极附近的电子急剧增多，形成了产生第二波的“雪崩”效应，增加电子。

这个电子不断增多的过程成为气体放大。

2. ）雪崩过程发生在阳极附近，加上电子的质量远远小于阳离子的质量，因此电子很快被阳极吸收，在管内留下一个由大量阳离子构成的阳离子鞘包围着阳极。

之减小，直到电场强度不足以引起雪崩效应， 这时雪崩效应停止， 阳离子鞘停止生成，G-M 管进入恢复过程。

在电场的作用下，正离子鞘缓慢地向阴极移动，阳极附近的电场也随之恢复，使得与 G-M 管串联的电阻记录下一个电压脉冲。

3.）当阳离子到达阴极时会再次打出光电子， 如果这些电子再次形成离子放电的话,一个入射粒子就将产生多个信号了。

为了避免再次形成雪崩效应， 使得一个入射粒子只产生一个信号，在管内加入少量的卤素气体来吸收这部分电子。

3. 脉冲特性:1. ）坪曲线盖革计数器的计数率与电压有“坪”；在 VC 之后，计数率随着电压急速增大。

2. ）电源电压越大，负脉冲幅度越大；串联电阻越大，脉冲宽度较宽，幅度也较大。

衰变统计规律衰变统计规律：在放射性衰变过程中，对于某个特定的放射性核素，其衰变的发生是完全随机且不可预测的，但从大量的原子核来看，其衰变又呈现出一定的统计规律，即在某一固定时间段内，发生衰变的原子核数目是相对稳定的。

嘿，想象一下，这些放射性原子核就像是一群调皮的小精灵，它们可不会乖乖地按照我们期望的方式行动。

它们什么时候衰变，那完全是看它们自己的心情，没有任何规律可循，特别任性！但神奇的是，当把它们聚在一起形成一个庞大的群体时，它们的行为又好像被一只无形的大手给规范住了。

就好像这些小精灵在玩一个特别的游戏，每个小精灵都有可能随时“出局”，也就是发生衰变。

单个小精灵的行为是完全无法预料的，它可能下一秒就“出局”了，也可能等了好久都不“出局”。

但是呢，如果有一大群这样的小精灵，我们就会发现，在一段时间内，总会有差不多固定数量的小精灵“出局”。

这就好像它们虽然各自为战，但冥冥之中又遵循着某种神秘的规则。

比如说铀这种放射性元素吧，它的原子核就一直在玩着这个衰变的游戏。

在一大块铀矿石中，每时每刻都有铀原子核在发生衰变，但我们无法确切地知道下一个衰变的会是哪一个。

然而，通过长时间的观察和统计，我们可以大致算出在一定时间内会有多少铀原子核发生衰变。

这就像是我们虽然不知道彩票的中奖号码是多少，但我们可以通过统计数据大致了解到中奖的概率有多大。

而且啊，这种衰变统计规律在很多领域都有着重要的应用呢。

在核物理学中，科学家们通过研究这种规律来深入了解原子核的结构和性质；在医学上，利用放射性同位素的衰变规律可以进行疾病的诊断和治疗，比如放射性治疗癌症，就是根据衰变规律来精确控制辐射剂量的。

总之，衰变统计规律虽然听起来很神秘，但它却在我们的生活和科学研究中发挥着重要的作用。

它让我们对这个世界的认识更加深入，也为我们解决各种问题提供了有力的工具。

如果你对这些神奇的科学规律感兴趣，不妨去看看相关的科普书籍，或者上网搜索一些专业的科学网站，那里有更多有趣的知识等待着你去探索。

放射性衰变涨落统计规律一、实验目的1．验证放射性衰变的涨落规律；2．了解统计误差的意义，掌握计算统计误差的方法；3．统计检验放射性衰变涨落的概率分布类型；4．学会用列表法和作图法表示实验结果。

二、实验内容1．在相同的实验条件下，多次重复测量某放射源的计数；2．在相同的实验条件下，多次重复测量装置的放射性本底；3．用列表法和作图法表示实验结果；列出频数、频率统计和Χ2检验表；作放射源和本底计数的频数、频率、累积频率曲线图；4．作Χ2检验，确定放射源的本底计数的概率分布类型。

三、原理四、设备与装置1．点状Υ放射源；2．FD－3013型数字Υ辐射仪；3．ZDD3901石材放射性检测仪；4．FD－3017测氡仪；5．X-γ剂量率仪。

五、步骤1．按图放置好实验设备；2．检查仪器，并置于正常工作状态，3．选择测量时间，(对于FD3013、FD-3017仪器置于“１分”测量档)；4．连续测量装置的本底计数10次以上，并记录之；5．连续重量测量放射源的计数30次以上，并记录之。

六、编写实验报告1．按基础知识要求，将计数分组、列表、制图（频率直方图和累积概率曲线）；表1 .1实测频数、频率分布表2.使用均方误差公式σ=N1/2 和S求出均方误差；3．说明N1/2 的物理意义。

思考题：1.什么叫放射性衰变统计涨落规律？它服从什么规律？如何检验？2.σ的物理意义是什么？3.用单次测量结果与多次测量结果表示放射性测量结果时，为什么是Ｎ±Ｎ1/2，其物理意义是什么？4.为什么使用放射性的概率分布可以检查辐射仪的性能？5.对实验结果进行检验时，如何正确选择概率分布类型？附录：仪器操作FD3013型数字Υ辐射仪装入两节1号电池，注意正确放入电池的极性，正极朝里，负极向外；将仪器手柄部旋钮开关打开置于“ON”，预热5分钟；测量时将底部开关置于CPM/CPS（计数/分钟，计数/秒），测量时间为一分钟，每次测量结束，机器报警，记录数据，按手柄处红色按钮继续重复测量；测量要求于实验室固定点测量30次以上。

盖革-弥勒计数器及核衰变的统计规律盖革-弥勒计数器是一种用于测量放射性核素活度的仪器。

它基于核反应速率与放射性核素的活度之间的关系，通过测量辐射计数来估算样品的放射性活度。

本文将探讨盖革-弥勒计数器的工作原理以及核衰变的统计规律。

一、盖革-弥勒计数器的工作原理盖革-弥勒计数器主要由两个部分组成：探头和电子学装置。

探头是由放射性样品和闪烁体组成，通过放射线和闪烁效应将辐射计数转化成可感测的光脉冲。

电子学装置负责对探头输出的信号进行放大、滤波和数字化处理。

当探头接受放射性样品的辐射时，闪烁体被激发并发出光子。

这些光子与光导管中的正电子发生相遇，产生光电效应并产生电子-空穴对。

这些电子会经过倍增器的放大器，产生更多的电子-空穴对，最终形成一个能够被电子学装置记录和分析的电脉冲。

通过校准和标准曲线法，可以将盖革-弥勒计数器的输出辐射计数转化成样品的放射性活度。

在核废料储存和放射性医学诊断等领域中，盖革-弥勒计数器被广泛使用。

二、核衰变的统计规律核衰变是一种随机性过程，每个放射性核素的衰变和放射发生率并不是恒定值。

相反，这些过程遵循一些统计规律，包括：1.指数规律指数规律是最普遍的核衰变统计规律之一。

在这一规律下，放射性核素的活度随时间呈指数下降。

每个放射性核素的半衰期是指其放射性活度减半所需的时间。

每次单个核衰变的发生是一个独立的随机过程，发生的概率在时间上是均匀分布的。

2.泊松分布泊松分布是描述随机事件发生的分布。

在核衰变中，每次放射性衰变是一个随机过程，一个时间点上出现较多的衰变事件比出现较少的衰变事件的概率要小。

这种规律被称为泊松分布。

3.高斯分布高斯分布是另一种随机分布，常常用于描述实验测量误差。

在放射性核素活度的测量中，测量误差会引入高斯分布的误差，并将造成测量值与理论值之间存在一定差异。

结论盖革-弥勒计数器在核科学、医疗和环境监测等领域中起着重要作用。

这种仪器通过电子学装置对辐射计数进行放大和数字化处理，以确定放射性样品的含量和活度。