放射性衰变的基本规律

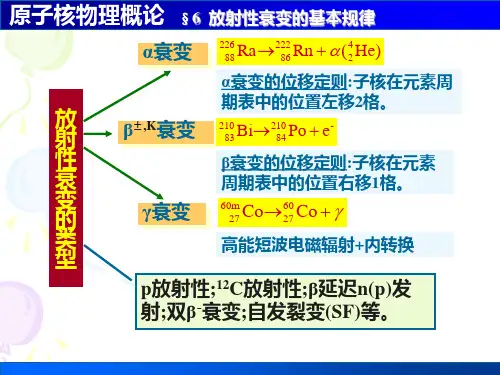
放射性衰变的规律与计算方法在我们生活的这个世界中，存在着许多肉眼无法直接察觉但却对我们的生活和科学研究有着重要影响的现象，放射性衰变就是其中之一。

放射性衰变是指不稳定的原子核自发地放出射线，转变为另一种原子核的过程。

理解放射性衰变的规律和掌握相应的计算方法，对于核物理学、地质学、医学等众多领域都具有至关重要的意义。

放射性衰变的规律可以用几个关键的概念来描述。

首先是半衰期，这是放射性衰变中一个极其重要的参数。

半衰期指的是放射性原子核数量衰变一半所需要的时间。

不同的放射性元素具有不同的半衰期，有的短至几毫秒，有的则长达数十亿年。

例如，碘-131 的半衰期约为 8 天，而铀-238 的半衰期约为 45 亿年。

另一个重要的概念是衰变常数。

衰变常数表示单位时间内一个放射性原子核发生衰变的概率。

它与半衰期之间存在着密切的关系，通过半衰期可以计算出衰变常数，反之亦然。

放射性衰变遵循指数衰减规律。

假设初始时刻某种放射性原子核的数量为 N₀，经过时间 t 后，剩余的原子核数量 N 可以用以下公式表示：N ＝ N₀ × e^（λt) ，其中λ就是衰变常数。

在实际应用中，我们经常需要根据已知条件来计算放射性衰变的相关参数。

比如，已知一种放射性物质的半衰期和初始数量，要计算经过一定时间后的剩余数量。

举个例子，假设我们有 100 克初始质量的放射性物质，其半衰期为10 天。

那么经过 20 天后，剩余的质量是多少呢？首先，我们需要计算衰变常数λ。

由于半衰期 T₁/₂＝ 10 天，根据公式λ ＝ ln2 ／ T₁/₂，可以算出λ ≈ 00693 ／10 ≈ 000693 。

然后，将 t ＝ 20 天，N₀＝ 100 克，λ ＝ 000693 代入公式 N ＝ N₀ × e^（λt) ，得到 N ＝ 100 × e^（－000693 × 20) ≈ 25 克。

放射性衰变的计算方法在许多领域都有着广泛的应用。

放射性衰变放射性核素的衰变规律放射性衰变是一种自然现象，指的是放射性核素在时间上逐渐减少自身的不稳定性。

本文将深入探讨放射性衰变的规律，并解释放射性核素的衰变过程。

一、放射性衰变的概念及特点放射性衰变是指放射性核素发生自发性的衰变现象，通过释放射线和/或粒子来达到更稳定的状态。

放射性衰变具有以下几个特点：1. 随机性：放射性衰变是完全随机的，不受任何外界影响。

2. 自发性：放射性核素在不依赖外界因素的情况下自行发生衰变。

3. 不可逆性：放射性核素一旦发生衰变，就无法逆转。

二、放射性衰变类型及衰变规律放射性衰变可以分为α衰变、β衰变和γ衰变。

下面将逐一对三种衰变类型进行阐述。

1. α衰变α衰变是指放射性核素通过释放氦离子（α粒子）来衰变。

α粒子包括两个质子和两个中子，其电荷为+2。

α衰变的衰变规律符合指数衰减定律，即放射性核素的数量随时间按指数函数减少。

衰变速率与放射性核素的数量成正比，可以用以下公式来计算α衰变的放射性核素数量N：N = N0e^(-λt)其中，N是某一时刻的放射性核素数量，N0是初始放射性核素数量，λ是衰变常数，t是经过的时间。

2. β衰变β衰变是指放射性核素通过释放电子（β粒子）或正电子（β+粒子）来衰变。

β衰变可以进一步分为β-衰变和β+衰变。

β-衰变的衰变规律与α衰变相似，也符合指数衰减定律。

β+衰变则是通过正电子与电子的相遇并湮灭，释放出γ光子。

3. γ衰变γ衰变是指放射性核素通过释放γ光子来衰变。

γ光子是高能量电磁波，具有较强穿透力。

γ衰变的衰变规律较为特殊，不依赖于时间或数量的指数函数。

放射性核素的γ衰变是连续的，直到衰变成一个稳定的核素。

三、半衰期和衰变常数半衰期是指放射性核素衰变至原始数量的一半所需的时间。

每种放射性核素都有其独特的半衰期。

半衰期与放射性核素的衰变常数有关，它们之间的关系可以用以下公式表示：t(1/2) = ln2 / λ其中，t(1/2)是半衰期，λ是衰变常数，而ln2是自然对数的2为底的对数。

放射性衰变规律在我们生活的这个世界里，存在着许多神奇而又神秘的现象，放射性衰变就是其中之一。

它不仅在科学研究中具有重要意义，还与我们的日常生活、医疗、能源等领域息息相关。

那么，什么是放射性衰变？它又遵循着怎样的规律呢？要理解放射性衰变，首先得知道什么是放射性。

放射性是指某些元素的原子核自发地放出射线的性质。

具有放射性的元素被称为放射性元素。

这些射线包括α射线、β射线和γ射线。

放射性衰变是指原子核由于自身的不稳定性，自发地发生变化，转变为另一种原子核，并同时放出射线的过程。

这个过程是随机的，不受外界条件的影响，比如温度、压力、化学状态等。

放射性衰变遵循着一定的规律。

其中最重要的规律之一就是指数衰变规律。

假设我们有一定量的某种放射性物质，其原子核的数量在初始时刻为 N₀。

经过时间 t 后，剩余的原子核数量 N 可以用下面的公式来表示：N ＝ N₀ × e^（λt) 。

这里的λ被称为衰变常数，它是每种放射性物质的特征值，反映了该物质衰变的快慢程度。

衰变常数λ与半衰期 T₁/₂有着密切的关系。

半衰期是指放射性物质的原子核数量衰变到初始数量的一半所需要的时间。

它们之间的关系可以用公式 T₁/₂＝ ln2 ／λ 来表示。

通过半衰期，我们可以比较直观地了解一种放射性物质的衰变速度。

半衰期短的放射性物质衰变速度快，而半衰期长的放射性物质衰变速度慢。

不同的放射性物质具有不同的半衰期。

比如，铀-238 的半衰期约为45 亿年，而碘-131 的半衰期只有8 天左右。

这意味着在相同的时间内，碘-131 会比铀-238 衰变掉更多的原子核。

放射性衰变的另一个重要规律是放射性活度的变化。

放射性活度是指单位时间内发生衰变的原子核数量。

它的单位是贝克勒尔（Bq）。

放射性活度也遵循指数衰变规律，随着时间的推移而逐渐减小。

放射性衰变的规律在许多领域都有重要的应用。

在考古学中，通过测量碳-14 的衰变程度，可以推算出古代文物的年代。

放射性衰变规律知识点总结放射性衰变是一种自然现象，指的是原子核自发地放出射线并转变为另一种原子核的过程。

这一过程遵循着一定的规律，理解这些规律对于研究原子核结构、核能利用以及辐射防护等方面都具有重要意义。

一、放射性衰变的类型放射性衰变主要有三种类型：α衰变、β衰变和γ衰变。

α衰变是指原子核放出一个α粒子（由两个质子和两个中子组成），从而使原子核的质量数减少 4，原子序数减少 2。

例如，铀 238 经过α衰变变成钍 234 。

β衰变分为β⁻衰变和β⁺衰变。

β⁻衰变是原子核中的一个中子转变为一个质子，并放出一个电子和一个反中微子；β⁺衰变则是一个质子转变为一个中子，同时放出一个正电子和一个中微子。

β衰变会导致原子核的原子序数发生变化，而质量数不变。

γ衰变通常伴随着α衰变或β衰变发生。

在原子核处于激发态时，会向低能态跃迁并放出γ射线（高能光子），这个过程不改变原子核的质子数和质量数，只是释放出多余的能量。

二、放射性衰变的规律1、指数衰变规律大多数放射性核素的衰变都遵循指数衰变规律。

假设在初始时刻（t ＝ 0 ），放射性原子核的数目为 N₀，经过时间 t 后，剩余的原子核数目为 N ，则它们之间的关系可以表示为：N ＝ N₀e^（λt) ，其中λ为衰变常数。

衰变常数λ表示单位时间内一个原子核发生衰变的概率，它的大小取决于原子核的种类。

λ越大，原子核衰变越快；反之，衰变越慢。

2、半衰期半衰期（T₁/₂）是指放射性原子核数目衰变到初始值一半所需的时间。

它与衰变常数λ的关系为：T₁/₂＝ 0693 ／λ 。

不同的放射性核素具有不同的半衰期，有的短至几秒甚至更短，有的则长达数十亿年。

例如，碘 131 的半衰期约为 8 天，而铀 238 的半衰期约为 45 亿年。

3、平均寿命平均寿命（τ）是指每个原子核衰变前存在的平均时间。

它与半衰期和衰变常数的关系为：τ ＝ 1 ／λ ，且τ ＝ 144 T₁/₂。

三、放射性衰变的影响因素放射性衰变是一个自发的过程，不受外界条件（如温度、压力、化学状态等）的影响。

放射性元素的衰变规律放射性元素的衰变规律是一个复杂的概念，但它也可以用于科学研究和工业应用。

下面我们来学习放射性元素的衰变规律：一，什么是放射性衰变？放射性衰变是指放射性元素（如铀，钚，钴等）的核子在变成新的元素时会发射出能量，释放出微粒子，这种能量和微粒子的结合就叫做放射性衰变。

它按照规律衰变，即物质的稳定性会逐渐减少，因此会产生放射性衰变，而这种衰变导致的放射性微粒子也叫放射性衰变产物。

二，放射性元素衰变的类型有哪些？放射性元素的衰变类型有放射性α衰落、β衰变和γ衰变等三种。

1、放射性α衰落放射性α衰落是放射性元素原子的核素衰变的一种，其特点是它会失去α粒子（包含2个质子和2个中子的原子核），并伴有少量的放射性能量释放出来；它在生物系统中属于敏感性放射性，并能在很短的距离内进入生物体，受到损伤。

2、放射性β衰变放射性β衰变是放射性元素原子核衰变的一种，它会释放β粒子，并伴有少量的放射性能量释放出来；同α衰变一样，它也具有比较高的放射性能量，并能产生较大的影响在生物体内。

3、放射性γ衰变放射性γ衰变是放射性元素原子核衰变的一种，它会伴有较多的放射性能量释放出来，但不同的是这种能量是以电磁波形式发出的。

本质上它就是一种高能量的电磁波，用于抗拒辐射或者在放射治疗中有其特殊作用。

三，放射性元素衰变的等离子体还原放射性元素衰变可以利用等离子体还原技术使之恢复到非放射性元素。

这是一种发展迅速的新技术，它可以把稳定元素从放射性材料中分离出来，并通过核反应将其转化为稳定元素。

这是一项具有重大潜在社会价值的革新性技术，可以使相关经济活动的成本大大降低。

四，放射性元素衰变的应用放射性衰变是一个自然发生的过程，但它也在日常生活中起到重要作用，是社会应用重要的利益相关者。

其中，它最常用来探测放射性材料，侦查盗尉犯等企业和机构中；此外，它还可以用于关键行业，例如核能水电站，放射性治疗，能源和医疗领域等，其他方面也以被越来越多地使用，为社会发展提供了重要的保证。

放射性衰变规律在我们的日常生活中，放射性衰变可能并不是一个经常被提及的话题，但它在科学、医学、工业等众多领域却有着至关重要的作用。

要理解放射性衰变规律，首先我们得明白什么是放射性。

放射性，简单来说，就是某些元素的原子核自发地放出射线的现象。

这些射线包括α射线、β射线和γ射线等。

而放射性衰变，则是指具有放射性的原子核由于放出某种粒子而转变为新核的过程。

放射性衰变的一个重要特点就是它的随机性。

这意味着我们无法准确预测某个原子核在何时会发生衰变。

但从大量原子核的整体行为来看，却存在着一定的规律。

放射性衰变遵循指数衰减规律。

假设在某一时刻，某种放射性物质的原子核数量为 N ，经过一段时间 t 后，剩余的原子核数量为 N' ，那么它们之间的关系可以用以下公式表示：N' ＝ N × e^（λt) 。

其中，λ被称为衰变常数，它反映了这种放射性物质衰变的快慢程度。

不同的放射性物质具有不同的衰变常数，因此它们的衰变速度也各不相同。

有的放射性物质衰变很快，在很短的时间内就会失去大部分放射性；而有的则衰变非常缓慢，可能需要经过数千年甚至更长时间才能有明显的变化。

例如，铀－238 的半衰期约为 45 亿年，这意味着经过 45 亿年，原有铀－238 原子核的数量会减少一半。

而碳－14 的半衰期约为 5730 年。

放射性衰变的规律在许多领域都有重要的应用。

在考古学中，通过测量碳－14 的含量，可以推断出古代遗物的年代。

生物体在死亡后，不再摄取新的碳－14 ，其体内原有的碳－14 会按照一定的规律衰变。

通过对比样品中碳－14 与正常环境中碳－14 的比例，就能估算出生物体死亡的时间。

在医学领域，放射性同位素被广泛用于诊断和治疗疾病。

例如，碘－131 可以用于治疗甲状腺疾病。

医生会根据碘－131 的衰变规律，计算出合适的剂量，以达到治疗效果的同时尽量减少对患者身体的损害。

在工业上，放射性物质可以用于检测材料的厚度、密度等参数。

放射性衰变规律在我们的日常生活中，虽然放射性衰变并不常见，但它在许多领域都有着至关重要的作用，从医学中的癌症治疗到地质年代的测定，从核能的利用到宇宙的探索。

那么，什么是放射性衰变？它又遵循着怎样的规律呢？要理解放射性衰变，首先得知道什么是放射性。

简单来说，放射性是指某些元素的原子核自发地放出射线的性质。

而这些具有放射性的原子核在放出射线的过程中，会转变成其他的原子核，这个过程就被称为放射性衰变。

放射性衰变主要有三种类型：α衰变、β衰变和γ衰变。

α衰变是指原子核放出一个α粒子（由两个质子和两个中子组成），从而导致原子核的质量数减少 4，原子序数减少 2。

β衰变则分为β⁻衰变和β⁺衰变。

β⁻衰变是原子核中的一个中子转变为一个质子，同时放出一个电子和一个反中微子；β⁺衰变则是一个质子转变为一个中子，同时放出一个正电子和一个中微子。

γ衰变一般不改变原子核的质子数和质量数，只是原子核从激发态跃迁到较低能态时放出γ射线（一种高能电磁波）。

放射性衰变遵循着一定的规律，其中最重要的就是指数衰变规律。

假设我们有一定数量的某种放射性原子核，在经过一段时间后，这些原子核会发生衰变，数量减少。

而减少的数量与当前存在的原子核数量成正比。

如果我们用 N 表示在某个时刻 t 尚未衰变的原子核数量，用 N₀表示初始时刻（t ＝ 0 ）的原子核数量，用λ表示衰变常数，那么它们之间的关系可以用公式 N ＝ N₀e^（λt) 来表示。

这个公式告诉我们，放射性原子核的数量会随着时间的推移呈指数形式减少。

衰变常数λ决定了衰变的快慢，λ越大，衰变就越快；反之，λ越小，衰变越慢。

不同的放射性核素具有不同的衰变常数，这也就意味着它们的衰变速度各不相同。

放射性衰变的半衰期也是一个重要的概念。

半衰期是指放射性原子核衰变一半所需的时间。

通过上述的指数衰变公式，我们可以推导出半衰期 T₁/₂与衰变常数λ的关系：T₁/₂＝ ln2 ／λ 。

半衰期是一个相对稳定的特征值，它不受外界条件的影响，只取决于原子核本身的性质。