化工原理习题——第三章

第三章习题解答3-1 某圆柱形固定床填充的催化剂直径为p d ，高为h ，试求等体积的当量直径及球形度。

解：h d d e 2p 346ππ=，32p 23h d d e = ()p 312p p 2322218)24(23d h h d h d d h d P P +=⋅⋅+⨯⎪⎭⎫ ⎝⎛=πππφ3-2 求20mm×20mm×25mm 的长方体颗粒的体积当量直径，表面积当量直径，比表面积当量直径及形状系数。

解：体积当量直径：mm V d ev 7.262520206633=⨯⨯⨯==ππ表面积当量直径：mm Sd es 8.282)252020202020(=⨯⨯+⨯+⨯==ππ比表面积当量直径：mm S V a d ea 1.232)252020202020(252020666=⨯⨯+⨯+⨯⨯⨯⨯=== 形状系数：86.08.287.26222222=====es ev es ev P s d d d d S S ππφ 3-3 由边长皆为2mm 的立方体，直径和高度均为2mm 的圆柱体及直径为3mm 的球体各10kg 组成的均匀颗粒床层，床层直径为0.2m ，高度为 1 m 。

已知颗粒的密度皆为1900kg/m 3，求床层的空隙率和颗粒的平均比表面积。

解： 床层体积：3220314.012.044m h d V b =⨯⨯==ππ颗粒体积：30158.01900310m V P =⨯= 床层空隙率：497.00314.00158.00314.0=-=-=bpb V V V ε 颗粒的平均比表面积：3球柱立a a a a ++=-13000002.0002.0002.06002.0002.0-=⨯⨯⨯⨯=m a 立 1223000002.0)002.0(4002.02)002.0(4-=⨯⨯⋅+⨯⨯=m a πππ柱 1322000003.066003.0003.0-==⨯⨯=m a ππ球 11 2.67676232000300030003---==++=++=mm m a a a a 球柱立 3-4 某形状近似球形的微小固体颗粒，其沉降运动处于斯托克斯定理区，试计算（1）该颗粒在20℃与200℃的常压空气中的沉降速度之比为多少？（2）该颗粒在20℃与50℃的水中的沉降速度之比为多少？[（1）1.44，（2）0.55]解：（1）20℃空气的粘度s Pa ⋅⨯=-51081.1μ，200℃空气的粘度s Pa ⋅⨯=-5'106.2μ，因沉降速度处于斯托克斯定律区，ρρ>>p ，故()()()()44.11081.1106.2181855''''22'=⨯⨯=--=--=--μρρμρρμρρμρρs s s s t t g d gd u u （2）20℃水的粘度s Pa ⋅⨯=-3101μ，50℃水的粘度s Pa ⋅⨯=-3'1055.0μ，因沉降速度处于斯托克斯定律区，并考虑到液体的密度随温度变化很小，故()()()()55.01011055.0181833'''''22'=⨯⨯=≈--=--=--μμμρρμρρμρρμρρs s p p p p t t g d g d u u 无论是气体还是液体，温度的改变主要是通过粘度的变化而影响沉降速度。

第三章沉降与过滤练习题一、填空：1、旋风分离器分离的是混合物，旋液分离器分离的是混合物，它们都属于混合物。

2、过滤操作有两种方式过滤和过滤。

4、恒压过滤时，过滤速度随时间增加而，洗涤速率随时间增加而，操作压差将随时间增加而。

( A、增加B、减少C、不变) 5、板框压滤机的洗涤速率是过滤终了速率的倍，叶滤机的洗涤速率是过滤终了速率的倍。

6、恒压过滤某悬浮液，过滤1小时得滤液10m3,，若不计介质阻力，再过滤2小时可共得滤液m3。

8、离心分离因数Kc= ，其值大小表示性能。

二、计算1、密度为1030 Kg/m3、直径为400μm的球形颗粒在150℃的热空气中降落，求其沉降速度。

(1.8m/s)2、求直径为80μm的玻璃球在20℃水中等自由沉降速度，已知玻璃球的密度2500 Kg/m3，水的密度为1000 Kg/m3，水在20℃时的黏度为0.001 Pas (5.23×10-3m/s)3、密度为2500 Kg/m3的玻璃球在20℃的水中和空气中以相同的速度沉降，求在这两种介质中沉降的颗粒直径之比值，假设沉降处于斯托克斯区。

(9.61)4、一种测定粘度的仪器由一钢球及玻璃筒组成，测试时筒内充满被测液体，记录钢球下落一定距离的时间，球的直径为6mm，下落距离为200mm，测试一种糖浆时记下的时间间隔为7.32s，此糖浆密度为1300Kg/m3，钢球的密度为7900 Kg/m3，求此糖浆的粘度。

(4.74Pas)5、直径为0.08mm，密度为2469 Kg/m3的玻璃球在温度300K和101.3kpa的空气中沉降。

计算自由沉降速度。

另有球形闪锌矿颗粒，密度为1000 Kg/m3，同样在空气中沉降，若其自由沉降速度与上述玻璃球相同，计算该颗粒的直径。

(0.443m/s，6.05×10-5m)6、悬浮液中固体颗粒浓度为0.025kg悬浮液，滤液密度为1120 m3，湿滤渣与其中固体的质量之比为 2.5kg/kg，试求与 1 m3滤液相对应得干滤渣量ω，Kg/m3(29.9)7、一叶滤机过滤面积为0.2 m2，过滤压差为200KPa，过滤开始1小时得滤液20m3，又过滤1小时，又得滤液10m3，此时过滤终止，在原压差下用5 m3水洗涤滤饼，求洗涤时间。

第三章 沉降与过滤沉 降【3-1】 密度为1030kg/m 3、直径为的球形颗粒在150℃的热空气中降落，400m μ求其沉降速度。

解 150℃时，空气密度，黏度./30835kg m ρ=.524110Pa s μ-=⨯⋅颗粒密度，直径/31030p kg m ρ=4410p d m -=⨯假设为过渡区，沉降速度为()(.)()./..1122223345449811030410179225225241100835p t p g u d m s ρρμρ--⎡⎤-⎡⎤⨯==⨯⨯=⎢⎥⎢⨯⨯⨯⎢⎥⎣⎦⎣⎦验算 .Re ..454101790．835=24824110p t d u ρμ--⨯⨯⨯==⨯为过渡区【3-2】密度为2500kg/m 3的玻璃球在20℃的水中和空气中以相同的速度沉降。

试求在这两种介质中沉降的颗粒直径的比值，假设沉降处于斯托克斯定律区。

解 在斯托克斯区，沉降速度计算式为()/218t p p u d g ρρμ=-由此式得（下标w 表示水，a 表示空气）()()2218= p w pw p a pat w ad d u g ρρρρμμ--=pw pad d =查得20℃时水与空气的密度及黏度分别为./,.339982 100410w w kg m Pa sρμ-==⨯⋅./,.35120518110a a kg m Pa sρμ-==⨯⋅已知玻璃球的密度为，代入上式得/32500p kg m ρ=.961pw pad d ==【3-3】降尘室的长度为10m ，宽为5m ，其中用隔板分为20层，间距为100mm ，气体中悬浮的最小颗粒直径为，气体密度为，黏度为10m μ./311kg m ，颗粒密度为4000kg/m 3。

试求：(1)最小颗粒的沉降速度；(2)若需要.621810Pa s -⨯⋅最小颗粒沉降，气体的最大流速不能超过多少m/s? (3)此降尘室每小时能处理多少m 3的气体？解 已知,/./.6336101040001121810pc p d m kg m kg m Pa sρρμ--=⨯===⨯⋅,,(1) 沉降速度计算 假设为层流区().()(.)./.26269811010400011001181821810pc p t gd u m sρρμ---⨯⨯-===⨯⨯验算 为层流..Re .66101000111000505221810pc t d u ρμ--⨯⨯⨯===<⨯，(2) 气体的最大流速。

三非均相物系分离沉降速度计算3.1 计算直径为1mm的雨滴在20℃空气中的自由沉降速度。

应用Stokes方程计算液体粘度3.2 将直径为6mm的钢球放入某液体中，下降距离位200mm时，所经历时间为7.32秒，此液体密度为1300[Kg/m3],钢球密度为7900[Kg/m3]，求此液体粘度为多少厘泊？降沉室的计算,设计型3.3 欲用降尘室净化温度为20℃、流量为2500(m3/h)的常压空气,空气中所含灰尘的密度为1800(kg/m3),要求净化的空气不含有直径大于10μm的尘粒,试求所需沉降面积为多大?若降尘室的底面宽2m,长5m,室内需要设多少块隔板?3.4用一多层降沉室除去炉中的矿尘。

矿尘最小粒径为8μm,密度为4000[kg/m3 ]。

降尘室内长4.1m,宽1.8m,高4.2m。

气体温度为427℃,粘度为3.4×10 -5 [N·S/ m2 ],密度为0.5[kg/m3 ],若每小时的炉气量为2160标准m3 ,试确定降尘室内隔板的间距及层数? (沉降处于斯托克斯定律区)3.5 用一截面为矩形的沟槽从炼油厂的废水中分离其中油滴，拟回收直径为2mm以上的油滴，槽宽为4.5m，深度为0.8m；在出口端除油后的水可不断从下部排出，而汇聚成层的油则从顶部移出。

油的密度为870[Kg/m3]，水温为20℃，每分钟处理废水为26m3,求所需槽的长度。

降沉室计算,操作型3.6 降沉室高2m、宽2m、长5m，用于矿石焙烧炉的降尘。

操作条件下气体的流量为25000[m3/h]；密度为0.6[kg/m3],粘度为0.03cP,固体尘粒的密度为4500[kg/m3 ]，求此降沉室能除去最小颗粒直径?并估计矿尘中直径为50μｍ的颗粒能被除去的百分率？3.7 气流中悬浮某种球形微粒，其中最小微粒为10μm,沉降处于斯托克斯区。

今用一多层隔板降尘室分离此气体悬浮物,已知降尘室长10m,宽5m,共21层,每层高100mm。

第三章沉降与过滤沉降【3-1】密度为1030kg/m 3、直径为400m μ的球形颗粒在150℃的热空气中降落，求其沉降速度。

解150℃时，空气密度./30835kg m ρ=，黏度.524110Pa sμ-=⨯⋅颗粒密度/31030p kg m ρ=，直径4410p d m -=⨯假设为过渡区，沉降速度为()(.)()./..1122223345449811030410179225225241100835p t p g u d m s ρρμρ--⎡⎤-⎡⎤⨯==⨯⨯=⎢⎥⎢⎥⨯⨯⨯⎢⎥⎣⎦⎣⎦验算.Re ..454101790．835=24824110p t d u ρμ--⨯⨯⨯==⨯为过渡区【3-2】密度为2500kg/m 3的玻璃球在20℃的水中和空气中以相同的速度沉降。

试求在这两种介质中沉降的颗粒直径的比值，假设沉降处于斯托克斯定律区。

解在斯托克斯区，沉降速度计算式为()/218t p p u d g ρρμ=-由此式得（下标w 表示水，a 表示空气）()()2218= p w pw p a pat w ad d u g ρρρρμμ--=pw pad d =查得20℃时水与空气的密度及黏度分别为./,.339982 100410w w kg m Pa s ρμ-==⨯⋅./,.35120518110a a kg m Pa sρμ-==⨯⋅已知玻璃球的密度为/32500p kg m ρ=，代入上式得.961pw pad d =【3-3】降尘室的长度为10m ，宽为5m ，其中用隔板分为20层，间距为100mm ，气体中悬浮的最小颗粒直径为10m μ，气体密度为./311kg m ，黏度为.621810Pa s -⨯⋅，颗粒密度为4000kg/m 3。

试求：(1)最小颗粒的沉降速度；(2)若需要最小颗粒沉降，气体的最大流速不能超过多少m/s?(3)此降尘室每小时能处理多少m 3的气体？解已知,/./.6336101040001121810pc p d m kg m kg m Pa sρρμ--=⨯===⨯⋅,,(1)沉降速度计算假设为层流区().()(.)./.26269811010400011001181821810pc p t gd u m sρρμ---⨯⨯-===⨯⨯验算..Re .66101000111000505221810pc t d u ρμ--⨯⨯⨯===<⨯．为层流(2)气体的最大流速max u 。

第三章 沉降与过滤沉 降【3-1】 密度为1030kg/m 3、直径为400m μ的球形颗粒在150℃的热空气中降落，求其沉降速度。

解 150℃时，空气密度./30835kg m ρ=，黏度.524110Pa s μ-=⨯⋅颗粒密度/31030p kg m ρ=，直径4410p d m -=⨯ 假设为过渡区，沉降速度为()(.)()./..1122223345449811030410179225225241100835p t p g u d m s ρρμρ--⎡⎤-⎡⎤⨯==⨯⨯=⎢⎥⎢⎥⨯⨯⨯⎢⎥⎣⎦⎣⎦验算 .Re ..454101790．835=24824110p t d u ρμ--⨯⨯⨯==⨯ 为过渡区【3-2】密度为2500kg/m 3的玻璃球在20℃的水中和空气中以相同的速度沉降。

试求在这两种介质中沉降的颗粒直径的比值，假设沉降处于斯托克斯定律区。

解 在斯托克斯区，沉降速度计算式为()/218t p p u d g ρρμ=- 由此式得（下标w 表示水，a 表示空气）()()2218= p w pw p a pat w ad d u g ρρρρμμ--=pw pad d =查得20℃时水与空气的密度及黏度分别为./,.339982 100410w w kg m Pa s ρμ-==⨯⋅ ./,.35120518110a a kg m Pa s ρμ-==⨯⋅已知玻璃球的密度为/32500p kg m ρ=，代入上式得.961pw pad d ==【3-3】降尘室的长度为10m ，宽为5m ，其中用隔板分为20层，间距为100mm ，气体中悬浮的最小颗粒直径为10m μ，气体密度为./311kg m ，黏度为.621810Pa s -⨯⋅，颗粒密度为4000kg/m 3。

试求：(1)最小颗粒的沉降速度；(2)若需要最小颗粒沉降，气体的最大流速不能超过多少m/s? (3)此降尘室每小时能处理多少m 3的气体？解 已知,/./.6336101040001121810pc p d m kg m kg m Pa s ρρμ--=⨯===⨯⋅,, (1) 沉降速度计算 假设为层流区().()(.)./.26269811010400011001181821810pc p t gd u m s ρρμ---⨯⨯-===⨯⨯验算..Re .66101000111000505221810pc t d u ρμ--⨯⨯⨯===<⨯． 为层流(2) 气体的最大流速max u 。

d 2 (ρ s -ρ ) u t 218μ第三章机械分离一、名词解释（每题 2 分）1. 非均相混合物物系组成不同，分布不均匀，组分之间有相界面 2. 斯托克斯式u r = ⋅r3. 球形度ϕ s非球形粒子体积相同的球形颗粒的面积与球形颗粒总面积的比值 4. 离心分离因数离心加速度与重力加速度的比值 5. 临界直径 dc离心分离器分离颗粒最小直径6．过滤利用多孔性介质使悬浮液中液固得到分离的操作 7. 过滤速率单位时间所产生的滤液量8. 过滤周期间歇过滤中过滤、洗涤、拆装、清理完成一次过滤所用时间9. 过滤机生产能力过滤机单位时间产生滤液体积 10. 浸没度转筒过滤机浸没角度与圆周角比值二、单选择题（每题 2 分）1、自由沉降的意思是_______。

Ａ颗粒在沉降过程中受到的流体阻力可忽略不计 Ｂ颗粒开始的降落速度为零，没有附加一个初始速度Ｃ颗粒在降落的方向上只受重力作用，没有离心力等的作用 Ｄ颗粒间不发生碰撞或接触的情况下的沉降过程 D2、颗粒的沉降速度不是指_______。

Ａ等速运动段的颗粒降落的速度Ｂ加速运动段任一时刻颗粒的降落速度 Ｃ加速运动段结束时颗粒的降落速度Ｄ净重力（重力减去浮力）与流体阻力平衡时颗粒的降落速度B3、对于恒压过滤_______。

A滤液体积增大一倍则过滤时间增大为原来的√2倍B滤液体积增大一倍则过滤时间增大至原来的2倍C滤液体积增大一倍则过滤时间增大至原来的4倍D当介质阻力不计时,滤液体积增大一倍,则过滤时间增大至原来的4倍D4、恒压过滤时，如介质阻力不计，滤饼不可压缩，过滤压差增大一倍时同一过滤时刻所得滤液量___。

Ａ增大至原来的2倍Ｂ增大至原来的4倍Ｄ增大至原来的1.5倍C5、以下过滤机是连续式过滤机_______。

Ａ箱式叶滤机Ｂ真空叶滤机Ｃ回转真空过滤机Ｄ板框压滤机C6、过滤推动力一般是指______。

Ａ过滤介质两边的压差Ｂ过滤介质与滤饼构成的过滤层两边的压差Ｃ滤饼两面的压差Ｄ液体进出过滤机的压差B7、回转真空过滤机中是以下部件使过滤室在不同部位时，能自动地进行相应的不同操作：______。

第三章 非均相物系的分离一、填空题：1．⑴一球形石英颗粒，在空气中按斯托克斯定律沉降，若空气温度由20°C 升至50°C ，则其沉降速度将 。

⑵降尘室的生产能力只与降尘室的 和 有关，而与 无关。

解⑴下降 ⑵长度 宽度 高度2．①在除去某粒径的颗粒时，若降尘室的高度增加一倍，则沉降时间 ，气流速度 ，生产能力 。

②在滞流（层流）区，颗粒的沉降速度与颗粒直径的 次方成正比；在湍流区，颗粒的沉降速度与颗粒直径的 次方成正比。

解①增加一倍 ， 减少一倍 ， 不变 ②2 ， 1/2沉降操作是指在某种 中利用分散相和连续相之间的 差异，使之发生相对运动而实现分离的操作过程。

沉降过程有 沉降和 沉降两种方式。

答案：力场；密度；重力；离心3．已知q 为单位过滤面积所得滤液体积V/S ，e e e S V q V /，为为过滤介质的当量滤液体积（滤液体积为e V 时所形成的滤饼层的阻力等于过滤介质的阻力），在恒定过滤时，测得2003740/+=∆∆q q τ，过滤常数K ＝ ，e q = 。

解0.000535 ， 0.05354．⑴间歇过滤机的生产能力可写为Q ＝V/∑τ，此外V 为 ，∑τ表示一个操作循环所需的 ，∑τ等于一个操作循环中 ， 和 三项之和。

一个操作循环中得到的滤液体积 ，总时间 ，过滤时间τ ，洗涤时间τw ， 辅助时间τD⑵．一个过滤操作周期中，“过滤时间越长，生产能力越大”的看法是 ，“过滤时间越短，生产能力越大”的看法是 。

过滤时间有一个 值，此时过滤机生产能力为 。

不正确的 ，不正确的 ， 最适宜 ， 最大⑶．过滤机操作循环中，如辅助时间τ越长则最宜的过滤时间将 。

⑶ 越长(4). 实现过滤操作的外力可以是 、 或 。

答案：重力；压强差；惯性离心力5．⑴在过滤的大部分时间中， 起到了主要过滤介质的作用。

⑵最常见的间歇式过滤机有 和 连续式过滤机有 。

⑶在一套板框过滤机中，板有 种构造，框有 种构造。

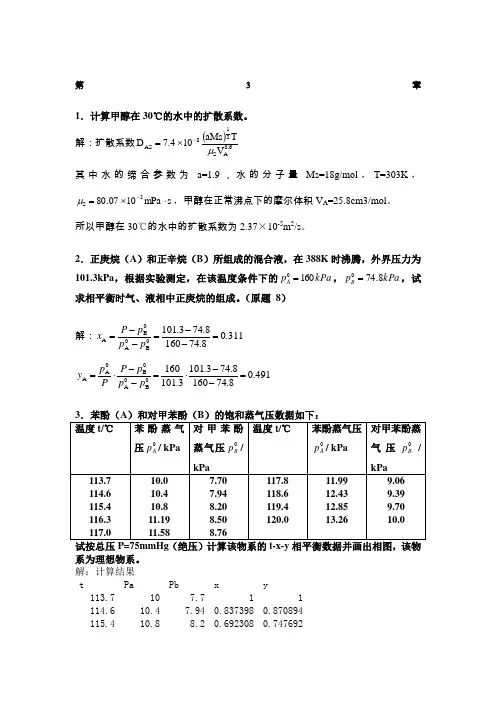
第3章1．计算甲醇在30℃的水中的扩散系数。

解：扩散系数()6.0AS 218AS V TaMs 104.7D μ-⨯=其中水的缔合参数为a=1.9，水的分子量Ms=18g/mol ，T=303K ，s mPa 1007.802S ⋅⨯=-μ，甲醇在正常沸点下的摩尔体积V A =25.8cm3/mol 。

所以甲醇在30℃的水中的扩散系数为2.37×10-5m 2/s 。

2．正庚烷（A ）和正辛烷（B ）所组成的混合液，在388K 时沸腾，外界压力为101.3kPa ，根据实验测定，在该温度条件下的kPa p A1600=，kPa p B 8.740=，试求相平衡时气、液相中正庚烷的组成。

（原题 8）解：311.08.741608.743.1010B 0A 0B A =--=--=p p p P x 491.08.741608.743.1013.1011600B 0A 0B 0A A =--⋅=--⋅=p p p P P p y系为理想物系。

解：计算结果 t Pa Pb x y 113.7 10 7.7 1 1 114.6 10.4 7.94 0.837398 0.870894 115.4 10.8 8.2 0.692308 0.747692116.3 11.19 8.5 0.557621 0.623978 117 11.58 8.76 0.439716 0.509191 117.8 11.99 9.06 0.320819 0.384662 118.6 12.43 9.39 0.200658 0.249418 119.4 12.85 9.7 0.0952380.122381120 13.26 10 0 0绘图113114115116117118119120℃x(y)0.00.20.40.60.81.0yx4．将含苯摩尔分数为0.5，甲苯摩尔分数为0.5的溶液加以汽化，汽化率为1/3，已知物系的相对挥发度为2.47，试计算：（1）作简单蒸馏时，气相与液相产物的组成；（2）作平衡蒸馏时，气相与液相产物的组成；解：（1）作简单蒸馏时，设液相产物的组成为x 2。

第三章流体通过颗粒层的流动一、基本知识1.下列关于非均相物系的举例及说明中错误的是。

甲：泡沫液，是液气组成的非均相物质，其中分散相是液体，分散介质是气体。

乙：乳浊液，是液固组成的非均相物质，其中连续相是液体，分散介质是固体。

丙：烟尘气，是气固组成的非均相物质，其中连续相是气体，分散介质是固体。

丁：雾沫气，是气液组成的非均相物质，其中分散相是液体，分散介质是气体。

①甲、乙②乙、丙③丙、丁④丁、甲2.下面论断中正确的有。

①单位体积固体颗粒所具有的表面积称为该固体颗粒的比表面积②根据不同方面的等效性(质量等效、体积等效、比表面积等效等)，可以定义不同的当量直径③形状系数是与非球形颗粒体积相等的球的表面积除以非球形颗粒的表面积的商④对于球形颗粒，只要一个参数，即颗粒直径便可惟一地确定其体积、表面积和比表面积⑤对于非球形颗粒，必须定义两个参数(通常定义体积当量直径和形状系数)才能确定其体积、表面积和比表面积3.下面有关颗粒群论断中正确的是。

①在任何颗粒群中，都存在一定的尺寸(粒度)分布②颗粒粒度的测量方法有筛分法、显微镜法、沉降法、电阻变化法、光散射与衍射法、表面积法等③对于大于70μm的颗粒，也就是工业固定床经常遇到的情况，常采用一套标准筛进行测量(筛分分析)④筛分使用的标准筛系金属丝网编织而成，各国习用筛的开孔规格各异，常用的泰勒制是以每英寸边长上的孔数为筛号或称目数4.下面有关颗粒群筛分结果论断中正确的有。

①筛分结果可用分布函数和频率函数图示②分布函数曲线上对应于某一尺寸dpi的分布函数Fi值表示直径小于dpi的颗粒占全部试样的质量分率，而该批颗粒的最大直径dp,max。

处，其分布函数Fi的值为1③频率分布曲线上在一定粒度范围内的颗粒占全部颗粒的质量分率等于该粒度范围内频率函数曲线下的面积，而频率分布函数曲线下的全部面积等于l④颗粒群的任何一个平均直径都不能全面代替一个分布函数5.颗粒的比表面积α和床层的比表面αB及床层的空隙率ε之间的关系式为。

第三章 非均相混合物分离及固体流态化1．颗粒在流体中做自由沉降，试计算（1）密度为2 650 kg/m 3，直径为0.04 mm 的球形石英颗粒在20 ℃空气中自由沉降，沉降速度是多少？（2）密度为2 650 kg/m 3，球形度6.0=φ的非球形颗粒在20 ℃清水中的沉降速度为0.1 m/ s ，颗粒的等体积当量直径是多少？（3）密度为7 900 kg/m 3，直径为6.35 mm 的钢球在密度为1 600 kg/m 3的液体中沉降150 mm 所需的时间为7.32 s ，液体的黏度是多少？解：（1）假设为滞流沉降，则：2s t ()18d u ρρμ-= 查附录20 ℃空气31.205kg/m ρ=，s Pa 1081.15⋅⨯=-μ，所以，()()()m 1276.0s m 1081.11881.9205.126501004.018523s 2t =⨯⨯⨯-⨯⨯=-=--μρρg d u 核算流型：3t 51.2050.12760.04100.3411.8110du Re ρμ--⨯⨯⨯===<⨯ 所以，原假设正确，沉降速度为0.1276 m/s 。

（2）采用摩擦数群法()()s 123t 523434 1.81102650 1.2059.81431.93 1.2050.1g Re u μρρξρ---=⨯⨯-⨯==⨯⨯ 依6.0=φ，9.431Re 1=-ξ，查出：t e t 0.3u d Re ρμ==，所以： 55e 0.3 1.8110 4.50610m 45μm 1.2050.1d --⨯⨯==⨯=⨯ （3）假设为滞流沉降，得：2s t()18d g u ρρμ-= 其中 s m 02049.0s m 32.715.0t ===θh u将已知数据代入上式得：()s Pa 757.6s Pa 02049.01881.91600790000635.02⋅=⋅⨯⨯-=μ 核算流型t 0.006350.020*******.0308116.757du Re ρμ⨯⨯===< 2．用降尘室除去气体中的固体杂质，降尘室长5 m ，宽5 m ，高4.2 m ，固体杂质为球形颗粒，密度为3000 kg/m 3。

第三章沉降与过滤沉 降【 3-1 】 密度为 1030kg/m 3、直径为 400 m 的球形颗粒在 150℃的热空气中降落，求其沉降速度。

解 150℃时，空气密度0.835kg / m 3 ，黏度 2.41 10 5 Pa s颗粒密度p 1030kg / m3，直径 d p 4 10 4 m假设为过渡区，沉降速度为4 g 2 ( p)214 9 81 2 103013234u td p( . ) ( ) 4 101.79 m / s225225 2.41 10 50.835d p u t44101 79 0．835验算Re=.24 82 41 105..为过渡区3【 3-2 】密度为 2500kg/m 的玻璃球在 20℃的水中和空气中以相同的速度沉降。

解 在斯托克斯区，沉降速度计算式为u td 2ppg / 18由此式得（下标w 表示水， a 表示空气）18pw d pw2( pa )d pa2 u t =gwad pw ( d pa(pa )wpw)a查得 20℃时水与空气的密度及黏度分别为w998 2 3w 1 . 004 10 3 . kg / m , Pa s 1 205 3a1 81 10 5 Pa sa . kg / m , .已知玻璃球的密度为p2500 kg / m 3 ，代入上式得dpw( 2500 1 205 ) 1 . 004 10.d pa( 2500998 2 1 . 81 10. )359.61【 3-3 】降尘室的长度为10m ，宽为 5m ，其中用隔板分为 20 层，间距为 100mm ，气体中悬浮的最小颗粒直径为10 m ，气体密度为1.1kg / m 3 ，黏度为 21.8 10 6 Pa s ，颗粒密度为4000kg/m 3。

试求： (1) 最小颗粒的沉降速度；(2) 若需要最小颗粒沉降，气体的最大流速不能超过多少m/s (3) 此降尘室每小时能处理多少m 3 的气体解 已知 d pc10 10 6 m, p4000kg / m 3 ,1.1kg / m 3 ,21.8 10 6 Pa s(1) 沉降速度计算假设为层流区gd pc 2 (p) 9 . 81 ( 10 10 6 2 ( 4000 1 1u t)6 . ) 0.01m / s1818 21.8 10d pc u t10 10 6 0 01 1 1000505． 2 验算 Re21 8 10 6 为层流.(2) 气体的最大流速 umax 。

第三章 沉降与过滤沉 降【3-1】 密度为1030kg/m 3、直径为400m μ的球形颗粒在150℃的热空气中降落，求其沉降速度。

解 150℃时，空气密度./30835kg mρ=，黏度.524110Pa sμ-=⨯⋅颗粒密度/31030p kg m ρ=，直径4410p d m -=⨯ 假设为过渡区，沉降速度为()(.)()./..1122223345449811030410179225225241100835p t p g u d m s ρρμρ--⎡⎤-⎡⎤⨯==⨯⨯=⎢⎥⎢⎥⨯⨯⨯⎢⎥⎣⎦⎣⎦验算.R e ..454101790．835=24824110p t d u ρμ--⨯⨯⨯==⨯为过渡区【3-2】密度为2500kg/m 3的玻璃球在20℃的水中和空气中以相同的速度沉降。

试求在这两种介质中沉降的颗粒直径的比值，假设沉降处于斯托克斯定律区。

解 在斯托克斯区，沉降速度计算式为()/218t p p u d g ρρμ=-由此式得（下标w 表示水，a 表示空气）()()2218=pw p wp a pat wad d u gρρρρμμ--=pw pad d =查得20℃时水与空气的密度及黏度分别为./,.339982 100410w w kg m Pa s ρμ-==⨯⋅./,.35120518110a a kg m Pa s ρμ-==⨯⋅已知玻璃球的密度为/32500p kg m ρ=，代入上式得.961pw pad d =【3-3】降尘室的长度为10m ，宽为5m ，其中用隔板分为20层，间距为100mm ，气体中悬浮的最小颗粒直径为10m μ，气体密度为./311kg m ，黏度为.621810Pa s -⨯⋅，颗粒密度为4000kg/m 3。

试求：(1)最小颗粒的沉降速度；(2)若需要最小颗粒沉降，气体的最大流速不能超过多少m/s? (3)此降尘室每小时能处理多少m 3的气体？解 已知,/./.6336101040001121810p c p d m k g m k g m P a sρρμ--=⨯===⨯⋅,, (1) 沉降速度计算 假设为层流区().()(.)./.26269811010400011001181821810p c p t gd u m sρρμ---⨯⨯-===⨯⨯验算..R e.66101000111000505221810pc t d u ρμ--⨯⨯⨯===<⨯． 为层流(2) 气体的最大流速m ax u 。

《化工原理》第三章选择题汇总姓名学号1、由重力沉降时，Rep在（）区时，颗粒的形状系数φ对沉降速度u t影响最大。

A、斯托克斯定律区：10-3<Rep<2B、艾伦定律区：2<Rep<500C、牛顿定律区：500<Rep<2×1052、直径为65微米的石英颗粒（密度为2600kg/m3）在20℃水中（密度为998kg/m3，粘度1cp）的沉降速度u t=( )m/s。

A、0.37B、0.037C、0.0037D、0.000373、在降尘室中，微粒在介质中的沉降过程为（）过程。

A、加速B、匀速C、先加速后匀速D、先加速后减速4、当固体微粒在大气中沉降是层流区域时，以（）的大小对沉降速度的影响最为显著。

A、颗粒密度B、空气粘度C、颗粒直径5、密度为3000kg/m3的粒子在60的空气（ρ=1.06kg/m3μ=2×10-5 pa.s）中沉降，则服从斯托克斯公式的最大直径为（）μmA、61B、6.1C、612D、无法确定6、球形粒子在重力作用下于流体层流区中沉降时的阻力系数为（）A、64/ReB、24/ReC、0.44D、17、固体微粒直径为0.315μm的悬浮液称为（）A、粗粒子悬浮液B、细粒子悬浮液C、浑蚀液D、胶体8、在滞流区颗粒的沉降速度正比于（）A、（p8-p）的1/2次方B、μ的零次方C、粒子直径的0.5次方D、粒子直径的平方9、自由沉降的意思是（）A、颗粒在沉降过程中受到的流体阻力可忽略不计B、颗粒开始的降落速度为零，没有附加一个初始速度C、颗粒在降落的方向上只受重力作用，没有离心力等的作用D、颗粒间不发生碰撞或接触的情况下的沉降过程10、颗粒的沉降速度不是指（）A、等速运动段的颗粒降落的速度B、加速运动段任一时刻颗粒的降落速度C、加速运动段结束时颗粒的降落速度D 、净重力（重力减去浮力）与流体阻力平衡时颗粒的降落速度11、欲提高降尘室的生产能力，主要的措施是（ ）A 、提高降尘室的高度B 、延长沉降时间C 、增大沉降面积12、要使微粒从气流中除去，必须使微粒在降尘室内的停留时间（ ）微粒的沉降时间A 、≥B 、≤C 、>D 、<13、以下说法不正确的是（ ）A 、降尘室的生产能力与设备底面积与含尘气流速度成正比B 、降尘室的生产能力与设备底面积与颗粒沉降速度成正比C 、与设备的高度无关14、下列对降尘室的描述错误的是（ ）A 、结构简单B 、阻力小C 、处理量大D 、分离效率高15、光滑球形颗粒在滞流区沉降的速度正比于（ ）A 、ρρ-pB 、μC 、d pD 、d p 216、下列与降尘室生产能力无关的参数是（ ）A 、高度B 、长度C 、宽度D 、微粒沉降速度17、当微粒与流体的相对运动属于滞流时，旋转半径为1m ，切线速度为20m.s -1，同一微粒在上述条件下的离心沉降速度等于重力沉降速度的（ ）倍。

第三章沉降与过滤一、填空题或选择1.悬浮液属液态非均相物系，其中分散内相是指_____________；分散外相是指______________________________。

***答案***固体微粒，包围在微粒周围的液体2.含尘气体中的尘粒称为（）。

A.连续相；B.分散相；C.非均相。

***答案***B3.悬浮在静止流体中的固体微粒在重力作用下，沿重力方向作自由沿降时，会受到_____________三个力的作用。

当此三个力的______________时，微粒即作匀速沉降运动。

此时微粒相对于流体的运动速度，称为____________。

***答案***重力、阻力、浮力代数和为零沉降速度4.自由沉降是___________________________________。

***答案***沉降过程颗粒互不干扰的沉降5.当微粒在介质中作自由沉降时，若粒子沉降的Rep相同时，球形度越大的微粒，介质阻力系数越________。

球形粒子的球形度为_________。

***答案***小16.沉降操作是使悬浮在流体中的固体微粒，在_________力或__________力的作用下，沿受力方向发生运动而___________，从而与流体分离的过程。

***答案***重离心沉积7.球形粒子在介质中自由沉降时，匀速沉降的条件是_______________。

滞流沉降时，其阻力系数=____________.***答案***粒子所受合力的代数和为零24/Rep8.降尘宝做成多层的目____________________________________。

***答案***增大沉降面积，提高生产能力。

9.气体的净制按操作原理可分为________________________________________________________.旋风分离器属_________________。

***答案***重力沉降、离心沉降、离心沉降离心沉降10.离心分离因数是________________________________________________。

第三章 传热过程1、平壁炉的炉壁由三种材料组成，其厚度和导热系数列于本题附表。

习题1附表序 号 材 料 厚度δ/mm导热系数λ/W ⋅ m −1 ⋅ K −11（内层）耐火砖 200 1.07 2 绝热砖 100 0.14 3钢 645若耐火砖层内表面的温度t 1为1150°C ，钢板外表面温度t 4为30°C ，又测得通过炉壁的热损失为300W ⋅ m −2。

试计算传导传热的面积热流量。

若计算结果与实测的热损失不符，试分析原因并计算附加热阻。

解：33221141t t R q λ+λ+λ−=φ==45006.014.01.007.12.0301150++−=2m W 1243901.01120−⋅= 计算的面积热流量大于实侧值，说明平壁间接触不良，有空气层存在，产生了附加热阻，其值R 为：R = R 实测 − R 计算 = 901.0733.3(300301150332211−=λδ+λδ+λδ−−= 2.832m 2 ⋅ °C ⋅ W −12、φ 50mm ×5mm 的不锈钢管，导热系数λ1=16W ⋅ m −1 ⋅ K −1，其外包扎厚30mm 的石棉，导热系数λ2=0.2W ⋅ m −1 ⋅ K −1，石棉层外再包30mm 厚的保温灰，导热系数λ3=0.07W ⋅ m −1 ⋅ K −1。

若不锈钢管内壁温度为260°C ，保温层最外层的壁温为35°C ，问每米管长的热损失为多少？解：不锈钢管的内半径为r 1=20mm ，外半径r 2=25mm ，∴r 2/r 1 < 2，故可按算术平均求每米管长的平均面积，A= 2πr 1m m1L = 2π(0.025 + 0.02)/2 × 1 = 0.1413m 2石棉层内半径r 2=25mm ，外半径r 3=55mm2r r 23>，需按对数平均求传热面积 r=2m m 038.0025.0055.0ln025.0055.0=−A= 2πr 2m m2L = 2 × 3.14 × 0.038 × 1 = 0.239m 2保温灰层内半径r 3=0.055mm ，外半径r 4=0.085mmr=3m m 069.0055.0ln055.0085.0=−A m,3 = 2πr m3L = 2×3.14×0.069×1=0.433m 2故每m 管长的热损失为433.007.003.0239.02.003.01413.016005.035260Am Am Am t t L 33322211141×+×+×−=λδ+λδ+λδ−=φ=1m W 9.1386194.1225−⋅=3、某蒸汽管外包扎有二层厚度相等的绝热材料，外层的平均直径为内层平均直径的两倍，而外层的导热系数为内层的1/2，若将此两种绝热材料互换位置，各层厚度与原来的一样，设蒸汽管外壁温度及外层绝热层的外侧面温度与原来情况分别对应相等，各绝热材料的导热系数值不因互换位置而异，问哪种情况的散热小？解：多层圆筒壁的导热计算式为：222111Am Am tλδ+λδΔ=φ设下标1代表内层，下标2代表外层依题意：δ1 = δ2 = δ，λ2 =21λ1，dm 2=2dm1故 Am 2=2Am 1 (Am=πdm ⋅ L)互换前：1111111222111Am 2tAm 2Am t Am Am t λδΔ=⋅λδ+λδΔ=λδ+λδΔ=φ 互换后：112511111222111Am tAm 2Am tAm Am tλδΔ=λδ+⋅λδΔ=λδ+λδΔ=φ′ ∴ 8.0542Am t Am t 112511==δ⋅λ⋅Δδ⋅λ⋅Δ=φφ′计算表明外层材料换内层后散热小，即将导热系数小的材料放在内层为宜。

化工原理——非均相物系的分离习题及答案第三章非均相物系的分离一、选择与填空1、在滞流区，颗粒的沉降速度与颗粒直径的＿＿次方成正比，在湍流区颗粒的沉降速度与颗粒直径的＿＿次方成正比。

2、在恒压过滤时，如介质阻力不计，过滤压差增大一倍时同一时刻所得滤液量__________。

A 增大至原来的2倍B 增大至原来的4倍C 增大至原来的2倍 D增大至原来的1.5倍3、过滤基本方程式是基于＿＿＿＿推导出来的。

A 滤液在介质中呈湍流流动B 滤液在滤渣中呈湍流流动C 滤液在介质中呈层流流动D 滤液在滤渣中呈层流流动4、颗粒的沉降速度不是指（）。

A等速运动段的颗粒降落的速度 B加速运动段任一时刻颗粒的降落速度C加速运动段结束时颗粒的降落速度 D净重力(重力减去浮力)与流体阻力平衡时颗粒的降落速度5、叶滤机洗涤速率与最终过滤速率的比值为（）。

A 1/2B 1/4C 1/3D 16、过滤介质阻力忽略不计，滤饼不可压缩进行恒速过滤，如滤液量增大一倍，则（）。

CA操作压差增大至原来的倍 B操作压差增大至原来的4倍C操作压差增大至原来的2倍 D操作压差保持不变7、在降尘室中除去某粒径的颗粒时，若降尘室高度增加一倍，则颗粒的沉降时间____，气流速度____，生产能力____。

8、沉降雷诺准数Ret越大，流体粘性对沉降速度的影响____。

9、一球形石英粒子在空气中作滞流自由沉降。

若空气温度由20℃提高至50℃，则其沉降速度将____。

10、含尘气体通过长4m、宽3m、高1m的降尘室，颗粒的沉降速度为0.03m/s，则降尘室的最大生产能力为____m3/s。

11、根据过滤基本方程式（说明提高过滤机生产能力的措施是（最少写出三条）____、____、____。

12、以下说法中正确的是（）A． B. C. D.13、在板框压滤机中，若过滤压力差增加一倍，则过滤速率变为原来的___倍，生产能力为___倍。

（过滤介质阻力忽略不计，滤饼不可压缩）14、恒压过滤某种悬浮液（介质阻力可忽略，滤饼不可压缩），已知10min单位过滤面积上得滤液0.1m3。