根式和分数指数幂的互化及其化简运算专题含答案

2．1。

1指数与指数幂的运算第一课时根式根式［提出问题]（1）若x2＝9，则x是9的平方根,且x＝±3；(2）若x3＝64，则x是64的立方根，且x＝4;(3）若x4＝81，则x是81的4次方根，且x＝±3;(4）若x5＝－32，则x是－32的5次方根，且x＝－2。

问题1：观察(1)(3），你认为正数的偶次方根都是两个吗？提示:是．问题2:一个数的奇次方根有几个？提示:1个．问题3:由于22＝4，小明说,2是4的平方根;小李说，4的平方根是2，你认为谁说的正确？提示：小明．[导入新知]根式及相关概念（1）a的n次方根定义:如果x n＝a，那么x叫做a的n次方根，其中n〉1，且n∈N＊。

（2)a的n次方根的表示：n的奇偶性a的n次方根的表示符号a的取值范围n为奇数错误!Rn为偶数±错误![0，＋∞）（3)根式：式子错误!叫做根式,这里n叫做根指数，a叫做被开方数．［化解疑难]根式记号的注意点（1）根式的概念中要求n>1，且n∈N＊。

（2）当n为大于1的奇数时，a的n次方根表示为错误!(a∈R);当n为大于1的偶数时，错误!(a≥0)表示a在实数范围内的一个n次方根，另一个是－错误!，从而错误!n＝a.根式的性质［提出问题]问题1：错误!3，错误!3，错误!4分别等于多少？提示:2，－2，2.问题2:错误!，错误!，错误!，错误!分别等于多少?提示：－2,2,2,2.问题3：等式错误!＝a及（错误!)2＝a恒成立吗？提示：当a≥0时,两式恒成立；当a〈0时，a2＝－a,（a)2无意义．［导入新知］根式的性质(1）(错误!）n＝a（n为奇数时，a∈R；n为偶数时，a≥0，且n〉1）．(2)错误!＝错误!(3)错误!＝0。

(4）负数没有偶次方根．[化解疑难]（错误!)n与错误!的区别（1)当n为奇数，且a∈R时，有错误!＝(错误!)n＝a;(2)当n为偶数，且a≥0时，有错误!＝（错误!）n＝a。

4.1.1 n 次方根与分数指数幂（二）一、选择题 1、已知0a >=（ ）A.12aB.32aC.23aD.13a2、下列各式正确的是（ ）A. a =B. 01a =C.4=-D.π=-3、已知x 5=–243，那么x =（ ）A. 3B. –3C. –3或3D. 不存在4（ ）A. 2B. –2C. ±2D. 45、已知0a > ）A. 712aB.512aC. 56aD.13a6、下列根式、分数指数幂的互化中，正确的是（ ） A. 12()x =-B. 13x -=C. 34(),0)x x y y -=≠D.13y =7、已知10m ＝2，10n ＝4，则3210m n-的值为（ ）A. 2B.C.D.二、填空题8=______．9、120.5233274()(3)(0.008)825--+⨯=______．三、解答题10、计算：()12223018329.64272-⎛⎫⎛⎫⎛⎫---+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．11()1132081π3274-⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭. 12、（1）计算：12230311216π3125--⎛⎫⎛⎫+-+ ⎪⎪⎝⎭⎝⎭；（2）已知12,23x y ==参考答案1、【答案】D【分析】本题考查根式与分数指数幂的互化及其化简运算.23a=2113323aa aa-===.选D.2、【答案】D【分析】本题考查根式的化简运算.【解答】对于A=a，当a为负数时等式不成立，故A不正确；对于B，a0＝1，当a＝0时无意义，故B不正确；对于C4=-，左边为正，右边为负，故C不正确；对于Dπ=-，故D正确．选D.3、【答案】B【分析】本题考查根式的化简运算.【解答】∵x5=–243，∵x3==-．选B.4、【答案】A【分析】本题考查根式的化简运算.=|–2|=2，选A.5、【答案】B【分析】本题考查根式与分数指数幂的互化及其化简运算.【解答】512a a>=====，选B.6、【答案】C【分析】本题考查根式与分数指数幂的互化.【解答】 A.12x=-（x≥0），因此不正确；B.13x-=x≠0），因此不正确；C. )34,0xx yy-⎛⎫=≠⎪⎝⎭（xy＞0），因此正确；答案第1页，共3页D.13y=，因此不正确．选C.7、【答案】B【分析】本题考查分数指数幂的运算.【解答】3210m n-＝3221010m n ＝()()32121010m n ＝3212248、【答案】π-3【分析】本题考查根式的化简运算.π3==-．9、【答案】52【分析】本题考查分数指数幂的化简运算. 【解答】120.5233274()(3)(0.008)825--+⨯211332332314()3()2525⎛⎫⨯-⨯⨯ ⎪⎝⎭=-+⨯353422=-+=． 10、【答案】12.【分析】本题考查分数指数幂的化简运算.【解答】()1212232232301839223129.6=1=1=.427243322-⨯⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫---+--+- ⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭11、【答案】2.【分析】本题考查根式与分数指数幂的互化及其化简运算. 【解答】()1132081π3274-⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭11323221132⎛⎫⨯⨯- ⎪⎝⎭⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭5212233=--+=． 12、【答案】（1）41；（2）-.【分析】本题考查分数指数幂的化简运算以及根式的化简求值.【解答】（1）()()122131322333311216π3(531256)1------⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭=+-+=36+9-5+1=41；（2==将12,23x y==236==-=---答案第3页，共3页。

根式和分数指数幂例1 求使等式(a －3)(a 2－9)＝(3－a )a ＋3成立的实数a 的取值范围． 解(a －3)(a 2－9)＝(a －3)2(a ＋3)＝|a －3|a ＋3， 要使|a －3|a ＋3＝(3－a )a ＋3成立， 需⎩⎪⎨⎪⎧a －3≤0，a ＋3≥0，解得a ∈[－3,3]． 跟踪训练1 若a 2－2a ＋1＝a －1，求a 的取值范围．解 ∵a 2－2a ＋1＝|a －1|＝a －1，∴a －1≥0，∴a ≥1. 例2 化简：(1)4(3－π)4； (2)(a －b )2(a >b )；(3)(a －1)2＋(1－a )2＋3(1－a )3.解 (1)4(3－π)4＝|3－π|＝π－3. (2)(a －b )2＝|a －b |＝a －b .(3)由题意知a －1≥0，即a ≥1.原式＝a －1＋|1－a |＋1－a ＝a －1＋a －1＋1－a ＝a －1. 跟踪训练2 求下列各式的值：(1)7(－2)7； (2)4(3a －3)4(a ≤1)； (3)3a 3＋4(1－a )4. 解 (1)7(－2)7＝－2. (2)4(3a －3)4＝|3a －3|＝3|a －1|＝3－3a .(3)3a 3＋4(1－a )4＝a ＋|1－a |＝⎩⎪⎨⎪⎧1，a ≤1，2a －1，a >1.例3 设－3<x <3，求x 2－2x ＋1－x 2＋6x ＋9的值．解 原式＝(x －1)2－(x ＋3)2＝|x －1|－|x ＋3|，∵－3<x <3，∴当－3<x <1时，原式＝－(x －1)－(x ＋3)＝－2x －2； 当1≤x <3时，原式＝(x －1)－(x ＋3)＝－4.∴原式＝⎩⎪⎨⎪⎧－2x －2，－3<x <1，－4，1≤x <3.1．已知x 5＝6，则x 等于( )A. 6B.56 C ．－56 D ．±56 答案 B2．m 是实数，则下列式子中可能没有意义的是( ) A.4m 2 B.3m C.6m D.5－m 答案 C3．(42)4运算的结果是( )A ．2B ．－2C ．±2D ．不确定 答案 A4.3－8的值是________． 答案 －25.(a －b )2＋5(a －b )5的值是________． 答案 0或2(a －b )解析(a －b )2＋5(a －b )5＝|a －b |＋(a －b )＝⎩⎪⎨⎪⎧0，a ≤b ，2(a －b )，a >b .例1 用根式的形式表示下列各式(x >0)．25(1);x 53(2).x -解 (1) 25x ＝5x 2. (2)53x-＝13x 5.跟踪训练1 用根式表示2132x y -(x >0，y >0)．解221332121xy y x-=⋅=例2 把下列根式化成分数指数幂的形式，其中a >0，b >0.(1)5a 6； (2)13a 2； (3)4b 3a 2； (4)(－a )6.解65.a=23231.aa-==(3)4b3a2132133444242.bb a a aa--⎛⎫===⎪⎝⎭632.a a===跟踪训练2把下列根式化成分数指数幂：(1) 682；(2) a a(a>0)；(3)b3·3b2；(4)13x(5x2)2.解1776212(2)2;===313224();a a ====(3)2113333;b b b b=⋅=3591353511.()xx x-======例3计算下列各式(式中字母都是正数)：(1)10.5233177(0.027)2;1259-⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭解10.5233177(0.027)21259-⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭＝(30.027)2＋312527－259＝0.09＋53－53＝0.09.(2)211511336622(2)(6)(3);a b a b a b-÷-解原式＝211115326236[2(6)(3)]44.a b ab a+-+-⨯÷－－＝＝(3)111222.m mm m--+++解1111122222111122222().m m m mm mm m m m-----+++==+++跟踪训练3(1)化简：130.256178;86-⎛⎫⎛⎫⨯-+⎪ ⎪⎝⎭⎝⎭解 原式＝1111131(1)()36623334424481(2)2(2)(3)2223112.-⨯-+⨯+⨯+⨯=+++=(2)化简：213211113625;1546x yx y x y ---⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭解 212111132(1)()332261111362565(4)51546x y x yx y x y -⎛⎫------- ⎪⎝⎭--⎛⎫=⨯-⨯-⨯⨯ ⎪⎛⎫⎛⎫⎝⎭-- ⎪ ⎪⎝⎭⎝⎭110662424.x y y ==(3)已知11225,x x -+=求x 2＋1x 的值．解 由11225,x x-+=两边同时平方得x ＋2＋x －1＝25，整理，得x ＋x －1＝23，则有x 2＋1x＝23.例4 已知a >0，b >0，且a b ＝b a ，b ＝9a ，求a 的值．解 方法一 ∵a >0，b >0，又a b ＝b a ，1119()()(9),a b a bbba b a b a a ∴=⇒=⇒=81829993a a a ∴=⇒=⇒=方法二 ∵a b ＝b a ，b ＝9a ，∴a 9a ＝(9a )a ，即(a 9)a ＝(9a )a ，∴a 9＝9a ，a 8＝9，a ＝43.跟踪训练4 已知67x ＝27,603y ＝81，求3x －4y 的值．解 由67x＝33，3673,x =得由603y＝81，46033,y=得433y x-∴＝60367＝9＝32，∴4y －3x ＝2，故3x －4y＝－2. 1．化简238的值为( )A ．2B ．4C ．6D ．8 答案 B 2．1225-等于( )A ．25 B.125 C ．5 D.15答案 D3．下列根式与分数指数幂的互化正确的是( ) A ．－x ＝12()(0)x x ->B.6y 2＝13(0)y y <C ．340)xx -=>D ．130)xx -=≠答案 C4．(36a 9)4＝________.答案 a 25．计算122-⨯________．答案 16。

衔接点02根式、分式的化简
1、能熟练把二次根式化简为最简根式
2、了解分式和最简分式
3、能熟练应用分式基本性质约分和通分
1、初中知识再现
③
对点特训一：二次根式有意义的条件
对点特训二：求二次根式中的参数
对点特训三：二次根式的乘法与除法及其混合运算
对点特训四：最简二次根式
对点特训五：二次根式的加法与减法及其混合运算
A．点A B．点B
【答案】C
对点特训六：分母有理化
对点特训七：二次根式化简求值
对点特训八：分式的意义
对点特训九：分式的化简求值
精练
对点特训十：分式的基本性质
A．2a B．。

一：化根式为分数指数幂例1化简下列各式；1()xy-分析：将根式化为指数幂的形式，再利用有利数指数幂的运算性质进行化简．解：（１）原式＝11111112236363a b a b-+-+⋅==（２）原式＝111113312133222222()()()()()xy x y xy xy x y xy---⋅⋅⋅=⋅＝1122()()()1xy xy xy-⋅==评注：化简根式，尤其是根式中又有分数指数幂的代数式，通常化根式为分数指数幂，然后根据运算法则运算，同时要注意结果形式的统一．二：活用乘法公式例１化简：132111333311111x x x xx x x x-+-+-+++-解：原式＝12112111133333333321113333(1)(1)(1)(1)(1)(1)111x x x x x x x x xx x x x-+++-++-+-+++-＝12121133333311x x x x x x-+-+--=-=评注：要观察式中各项的结构，发现1,1x x-+分别是“立方差”和“立方和”，于是各个击破，达到化简之目的．计算过程中利用乘法公式进行因式分解，往往是计算简便．三：巧妙换元例４化简3221311)1111()1(222222+--++--+÷---+-+xxxxxxxxxxxxxx．分析：观察全式便能发现在此式中，形式上出现最多的是xx1+,而由乘法公式可知：2)1(1222-+=+xxxx．若令1x ax+=，原式的形式会变得相当简单．这种局部换元的方法在代数变形中是十分有效的．解：设xx1+＝a，则原式＝1)1()11(121)11(22222222+--∙-+--=+-+-÷---a a a a a a a a a a a a a a ＝)1(22+--a a a ＝a －１＝xx 1+－１ 评注：通过换元，可把分数指数幂转化为整数指数幂，把复杂运算转化为简单熟悉的运算，快速解决问题．四：利用性质例５ 计算：（１）211322110()(2)(2)3427---⋅-；（２）112111222111a a a a a ----+--+ 解：（１）原式＝2211332239643427()()()()24272964--⋅-=⋅-＝213234273297()()2964231616⋅-=⋅-= （２）原式＝11111111222221111122222(1)(1)1(1)1a a a a aaa a a a a aaa a a---------+-+-=--+-+＝11220aa---= 评注：在指数运算中，利用()()nn a bba-=这个性质，颠倒底数的分子分母的位置，直接把负指数幂化为整指数幂，反之亦然．若能巧妙利用1ppa a -⋅=这个性质进行代换，则可化难为简．简化运算过程．五：整体代入 例１ 若2121-+xx ＝３ ．求23222323-+-+--x x x x 的值．分析：从已知条件中解出a 的值，然后再代入求值，这种方法不可取，而应设法从整体寻求结果与条件的联系，进而整体代入．解：∵ 2121-+x x ＝３，两边平方得11222()9x x -+=， ∴1x x -+＝７∴2212()249247x xx x --+=+-=-=将2121-+xx ＝３两边立方得 2323-+xx ＝18∴23222323-+-+--x x x x ＝31247318=--． 评注：本题解法是求3322x x -+，22x x -+的值后，整体代入，这是数学中的整体代换的思想方法，在指数的有关运算中，若把已知的代数式视为一个整体，直接代入，常可避免局 部运算的烦琐和困难．。

不等式专题1．指数函数x y a =的图像经过点（2，16）则a 的值是（ ） A ．14 B ．12C ．2D ．4 【答案】D 【解析】 试题分析：设出指数函数，将已知点代入求出待定参数，求出指数函数的解析式即可．设指数函数为x y a =（a 0＞且a 1≠）,将（2，16）代入得216a =,解得a=4,所以x y 4=．考点：指数函数的定义、解析式、定义域和值域2．已知集合{}{}|1,|21xM x x N x =<=>，则MN =（ ）A ．∅B ．{}|0x x <C ．{}|1x x <D ．{}|01x x << 【答案】D 【解析】 试题分析：利用指数函数的单调性求出集合N 中的解集；利用交集的定义求出M N ．由题x N {x |21}{x |x 0}M {x |x 1}M N {X |0X 1}===∴=＞＞＜，＜＜考点：交集及其运算．3．下列各组函数是同一函数的是（ ）①()f x =()g x = ②2()21f x x x =--与2()21g t t t =-- ；③0()f x x =与01()g x x=； ④()f x x =与2()g x =。

A ．①② B ．②③ C ．③④ D ．①④ 【答案】B 【解析】试题分析：根据函数的定义域相同，对应关系也相同的两个函数是同一函数，进行判断即可．对于①，()()x 0x 0f x x =≤≤），g ），它们的对应关系不同，不是同一函数；对于②，22f x x 2x 1x Rg t t 2t 1x R =∈=∈（）﹣﹣（），（）﹣﹣（），它们的定义域相同，对应关系也相同，是同一函数；对于③，()0001f x x 1x 0x 0x x ==≠=≠（）（），g （），它们的定义域相同，对应关系也相同，是同一函数；对于④，()2,0f x x x 0,0x x x x x ≥⎧===≥⎨-<⎩（），g （），它们的定义域不同，对应关系也不同，不是同一函数；综上，是同一函数的为②③．考点：函数相等4．)31()3)((656131212132b a b a b a ÷-的结果是（ ）A ．6aB ．9abC ．abD ．－ 9a 【答案】D 【解析】试题分析：先计算系数，然后利用同底数幂的乘除运算求解．21152********36632623622399a b a b a b a b a +-+-⎛⎫⎛⎫-÷=-=- ⎪ ⎪⎝⎭⎝⎭．考点：根式与分数指数幂的互化及其化简运算．5．已知函数84)(2--=kx x x h 在[5，20]上是单调函数，则k 的取值范围是（ ） A ．]40,(-∞ B ．),160[+∞ C ．(,40][160,)-∞+∞ D ．∅ 【答案】C 【解析】试题分析：根据二次函数的图象和性质，若函数2h x 4x kx 8=（）﹣﹣在[5，20]上是单调函数，则区间[5，20]应完全在对称轴x 8k=的同侧，由此构造关于k 的不等式，解得k 的取值范围．函数2h x 4x kx 8=（）﹣﹣的对称轴为x 8k= 若函数2h x 4x kx 8=（）﹣﹣在[5，20]上是单调函数， 则58k ≤或58k≥,解得k 40≤或k 160≥, 所以k 的取值范围是40][160∞⋃+∞（﹣，，）． 考点：二次函数的性质．6．已知集合A ＝{x|x ＜a }，B ＝{x|1＜x ＜2}，且()R A C B R =，则实数a 的取值范围 （ ）A ．a ≤2B ．a ＜1C ．a ≥2D ．a ＞2 【答案】C 【解析】试题分析：由题意知集合A={x|x ＜a}，B={x|1＜x ＜2}，然后根据交集的定义和运算法则进行计算．∵集合A {x |x a}B {x |1x 2}==＜，＜＜， ∴R B {x |x 1=≤ðx 2}≥或，A B R,a 2R C =∴≥．考点：交、并、补集的混合运算．7．．已知1)(35++=bx ax x f 且,7)5(=f 则)5(-f 的值是（ ） A ．5- B ．7- C ．5 D ．7【答案】A 【解析】试题分析：因为5与﹣5 互为相反数，可借助于函数奇偶性求解． 5353f x ax bx 1f x ax bx 1=++∴=+（），（﹣）﹣﹣．f （x ）+f （﹣x ）=2 f 5f 52f 5275∴+===（）（﹣）（﹣）﹣﹣．考点：函数奇偶性的性质；函数的值．8．函数y=f （x ）的图象如图所示,观察图象可知函数y=f （x ）的定义域、值域分别是（ ）A ．[-5, 0]∪[2, 6], [0, 5]B ．[-5, 6], [ 0, +∞）C ．[-5, 0]∪[2, 6）, [0, +∞）D ．[-5, +∞）, [ 2, 5 ] 【答案】C 【解析】试题分析：函数的定义域即自变量x 的取值范围，即函数图象的横向分布；函数的值域即为函数值的取值范围，即为函数图象的纵向分布，由图可直观的读出函数的定义域和值域．函数的定义域即自变量x 的取值范围，由图可知此函数的自变量x [50][26∈﹣，，），函数的值域即为函数值的取值范围，由图可知此函数的值域为[0+∞，）． 考点：函数图象的作法；函数的值域．9．若不等式222424ax ax x x +-<+对任意实数x 均成立，则实数a 的取值范围是（ ）A ．(2,2)-B ．(,2)(2,)-∞-+∞ C ．(2,2]- D ．(,2)-∞【答案】C 【解析】试题分析：将原不等式整理成关于x 的二次不等式，结合二次函数的图象与性质解决即可，注意对二次项系数分类讨论．222ax 2ax 42x 4x a 2x 2a 2x 40++∴+﹣＜，（﹣）（﹣）﹣＜，当a ﹣2=0，即a=2时，恒成立，合题意．当a 20≠﹣时，要使不等式恒成立，需20a -<⎧⎨∆<⎩，解得﹣2＜a ＜2．所以a 的取值范围为（﹣2，2]． 考点：函数恒成立问题．10R 上的增函数，则a 的取值范围是（ ）A ．30a -≤＜B ．2a ≤-C ．a 0<D ．32a -≤≤- 【答案】D 【解析】试题分析：由函数f （x ）上R 上的增函数可得函数，设2g x x ax 5h x ax==（）﹣﹣﹣，（），则可知函数g （x ）在x 1≤时单调递增，函数h （x ）在1+∞（，）单调递增，且g 1h 1≤（）（），从而可求．()25,1,1x ax x f x ax x ⎧---≤⎪=⎨>⎪⎩是R 上的增函数, 设2g x x ax 5h x ax==（）﹣﹣﹣，（）,由分段函数的性质可知，函数2g x x ax 5=（）﹣﹣﹣在1]∞（﹣，单调递增，函数h x ax=（）在1+∞（，）单调递增，且g 1h 1≤（）（）, 120,326a a a a a ⎧-≥⎪⎪∴<∴-≤≤-⎨⎪--≤⎪⎩考点：函数单调性的性质；二次函数的性质．第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题（题型注释）11．y =的定义域为 ． 【答案】[4,5)(5,)⋃+∞【解析】试题分析：由分子根式内部的代数式大于等于0，分母不等于0列式求解x 的取值集合即可得到答案．40,4550x x x -≥⎧∴≤<⎨-≠⎩或x ＞5．∴5y x =-的定义域为[455+∞，）（，）． 考点：函数的定义域及其求法． 12．已知集合}1|{2==x x P ，集合}1|{==ax x Q ，若P Q ⊆，那么a 取值的集合为_________．【答案】{-1,0,1} 【解析】试题分析：先求出集合P ，讨论集合Q 是否为空集，然后根据Q P ⊆，求a 即可． ∵2P {x |x 1}==，∴P={x|x=1或x=﹣1}={﹣1，1}． 若a=0，则Q =∅，此时，满足条件Q P ⊆． 若a 0≠，则{}1Q x |ax 1{}a===，要使Q P ⊆． 则1a=1或-1，所以a=1或a=﹣1． 综上a=0或﹣1或1．考点：集合的包含关系判断及应用．13．把下列各数12113332523a (),b 2,c (),d (335===-=按从小到大的顺序排列为___ ______________【答案】c d a b <<<【解析】试题分析：根据指数幂的大小关系以及指数函数的单调性即可得到结论．1121113333322355c 000d a 24a b c d a b 3533=∴=∴∴（-）＜，＜（）＜（），＜＜，＞（）．＜，＜＜＜，考点：指数函数单调性的应用．14．函数(1)(0)()2(0)xf x x f x x +≤⎧=⎨>⎩，则(2)f -=【答案】 2 【解析】试题分析：利用分段函数的性质求解．∵函数(1)(0)()2(0)xf x x f x x +≤⎧=⎨>⎩，∴f （﹣2）=f （﹣1）=f （0）=f （1）=2． 考点：分段函数三、解答题（题型注释）15．（12分）设{|||6}A x Z x =∈<，{1,2,3},{3,4,5}B C ==，求： （Ⅰ）()ABC ；（Ⅱ）()A A C B C【答案】（Ⅰ） {}5,4,3,2,1,0,1,2,3,4,5-----;（Ⅱ） {}5,4,3,2,1,0-----． 【解析】试题分析：通过绝对值不等式的解法求出集合A ．（Ⅰ）求出B C ，然后求解A B C （）； （Ⅱ）求出B C ，然后求解A B C C （），即可求解A A B C C （）． 试题解析：{5,4A =----2分 （Ⅰ）由{3}BC =()A B C ∴={}5,4,3,2,1,0,1,2,3,4,5A =----- 6分（Ⅱ）由{}1,2,3,4,5B C =，{}A ()5,4,3,2,1,0C BC =----- 10分()A A C B C ∴{}5,4,3,2,1,0=----- 12分考点：交、并、补集的混合运算；绝对值不等式的解法． 16．（12分）设集合{}|14A x x =-<<，3|52B x x ⎧⎫=-<<⎨⎬⎩⎭，{}|122C x a x a =-<<．（Ⅰ）若C φ=，求实数a 的取值范围； （Ⅱ）若()C A B ⊆，求实数a 的取值范围．【答案】（Ⅰ）1]4∞（-，;（Ⅱ） 3,]4∞（-． 【解析】试题分析：（Ⅰ）由C =∅，列出关于a 的不等式，求出不等式的解集即可确定出实数a 的取值范围；（Ⅱ）分C 为空集与C 不为空集两种情况，根据C 为A 与B 交集的子集求出a 的范围即可．试题解析：（Ⅰ）∵C =∅ ∴122a a -≥ ∴14a ≤即实数a 的取值范围是14∞（-，． 5分（Ⅱ）当C =∅时，由（1）知14a ≤ 6分 当C ≠∅，3{1}2AB x x =-<<，且()C A B ⊆∴ 122322121a a a a -<⎧⎪⎪≤⎨⎪-≥-⎪⎩ 9分解得：1344a <≤ 11分 综上实数a 的取值范围是3,]4∞（-． 12分 考点：交、并、补集的混合运算． 17．（12分）已知函数1()f x x x=+（Ⅰ）判断函数的奇偶性，并加以证明； （Ⅱ）用定义证明()f x 在[1上是增函数； （Ⅲ）求出函数()fx 在[1的最值．【答案】（Ⅰ）略；（Ⅱ）略；（Ⅲ）2，3．【解析】 试题分析：（Ⅰ）根据函数奇偶性的定义即可判断函数的奇偶性，并加以证明； （Ⅱ）根据函数单调性的定义即可证明f（x ）在⎡⎣上是增函数；（Ⅲ）根据函数的单调性的性质即可求出函数f（x ）在⎡⎣的最值．试题解析：（Ⅰ）函数()f x 为奇函数，理由如下： 易知函数()f x 的定义域为：(,0)(0,)-∞+∞，关于坐标原点对称．又11()(()f x x x f x x x-=--=-+=- ∴()f x 在定义域上是奇函数． 4分（Ⅱ）设12,[1x x ∈且12x x <，则1212121212121212()(1)111()()()()()(1)x x x x f x f x x x x x x x x x x x ---=+-+=--=1212121x x x x 1x x 10≤≤≤∴>>，﹣，2121x x x x 0∴＞﹣＞．所以12()()f x f x <， 因此函数()f x在[1上是增函数． 9分 （Ⅲ）由（2）知()f x 的最小值是f （1）=2,最大值是f=312分考点：奇偶性与单调性的综合．18．（13分）已知函数()f x 是定义在R 上的奇函数，且当0x ≤时，2()2f x x x =+． （Ⅰ）现已画出函数()f x 在y 轴左侧的图象，如图所示，请补出完整函数()f x 的图象，并根据图象写出函数()f x 的增区间；（Ⅱ）求出函数()f x 的解析式和值域．【答案】（Ⅰ）（-1 ，1）；（Ⅱ） 222,(0)()2,(0)x x x f x x x x ⎧+≤⎪=⎨-+>⎪⎩，(,)-∞+∞．【解析】试题分析：（Ⅰ）因为函数为偶函数，故图象关于y 轴对称，由此补出完整函数f （x ）的图象即可，再由图象直接可写出f （x ）的增区间．（Ⅱ）可由图象利用待定系数法求出x ＞0时的解析式，也可利用偶函数求解析式，值域可从图形直接观察得到． 试题解析：（Ⅰ）因为函数为奇函数，故图象关于原点对称，补出完整函数图象如图（图略）所以()f x 的递增区间是（-1 ，1）． 6分 （Ⅱ）由于函数()f x 为奇函数，则()()f x f x -=- 又当0x ≤时，2()2f x x x =+． 设x ＞0，则﹣x ＜0，∴22()()[()2()]2f x f x x x x x =--=--+⋅-=-+所以0x >时，2()2f x x x =-+，故()f x 的解析式为222,(0)()2,(0)x x x f x x x x ⎧+≤⎪=⎨-+>⎪⎩．由图知()f x 的值域为(,)-∞+∞ 13分考点：二次函数的图象；函数的值域；函数解析式的求解及常用方法；函数的单调性及单调区间． 19．（13分）某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的一年收益与投资额成正比，其关系如图（1）；投资股票等风险型产品的一年收益与投资额的算术平方根成正比，其关系如图（2）．（注：收益与投资额单位：万元）（Ⅰ）分别写出两种产品的一年收益与投资额的函数关系；（Ⅱ）该家庭现有20万元资金，全部用于理财投资，问：怎么分配资金能使一年的投资获得最大收益，其最大收益是多少万元？【答案】（Ⅰ）1()(0)8f x x x =≥,()0)g x x =≥;（Ⅱ）3． 【解析】试题分析：（Ⅰ）由投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比，结合函数图象，我们可以利用待定系数法来求两种产品的收益与投资的函数关系； （Ⅱ）由（Ⅰ）的结论，我们设设投资债券类产品x 万元，则股票类投资为20﹣x 万元．这时可以构造出一个关于收益y 的函数，然后利用求函数最大值的方法进行求解．试题解析：（Ⅰ）设1()f x k x =，()g x k = 所以 11(1)8f k ==，21(1)2g k ==， 即1()(0)8f x x x =≥，()0)g x x =≥； 5分 （Ⅱ）设投资债券类产品x 万元， 则股票类投资为(20)x -万元，依题意得：()(20)y f x g x =+-8x =+(020)x ≤≤，令t =(0t ≤≤，则22082t ty -=+21(2)38t =--+，所以当2t =，即16x =万元时，收益最大，max 3y =万元． 13分 考点：函数模型的选择与应用．20．（13分） 定义在D 上的函数)(x f ,如果满足:对任意D x ∈,存在常数0M >, 都有|()|f x M ≤成立,则称()f x 是D 上的有界函数,其中M 称为函数()f x 的上界．已知函数()11124x xf x a ⎛⎫⎛⎫=+⋅+ ⎪ ⎪⎝⎭⎝⎭; 2211)(x m x m x g ⋅+⋅-= （I ）当1a =时,求函数()f x 在(),0-∞上的值域,并判断函数()f x 在(),0-∞上是否为 有界函数,请说明理由;（Ⅱ）若函数()f x 在[)0,+∞上是以3为上界的有界函数,求实数a 的取值范围; （Ⅲ）已知1->m ,函数()g x 在[]0,1上的上界是)(m T ,求)(m T 的取值范围． 【答案】（I ） 不是有界函数；（Ⅱ） []5,1-；（Ⅲ） ⎪⎭⎫⎢⎣⎡+∞+-,11m m ．【解析】试题分析：（Ⅰ）将a=1代入f （x ）可得11()124x xf x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭，利用指数函数的单调性判断出f （x ）在0∞（﹣，）上是单调递减函数，即可求得f x f 0（）＞（），从而得到f （x ）的值域，根据有界函数函数的定义，即可判断出f （x ）不是有界函数；（Ⅱ）根据有界函数的定义，可得|f x |3≤（）在[0+∞，）上恒成立，利用参变量分离转化为11422222x xxx a ⎛⎫⎛⎫-⋅-≤≤⋅- ⎪ ⎪⎝⎭⎝⎭在[0+∞，）上恒成立，令x t 2=，则t t t h 14)(--=，tt t p 12)(-=，问题转化为求h （t ）的最大值和p （t ）最小值，利用函数单调性的定义，分别判断出函数h （t ）和p （t ）的单调性，即可求得最值，从容求得a 的取值范围．试题解析：（I ）当1a =时,11()124x xf x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭,因为)(x f 在(),0-∞上递减,所以()(0)3f x f >=,即)(x f 在(),1-∞的值域为()3,+∞ 故不存在常数0M >,使|()|f x M ≤成立 ，所以函数()f x 在(),1-∞上不是有界函数 （Ⅱ）由题意知,3)(≤x f 在[)1,+∞上恒成立．试卷第11页，总11页3)(3≤≤-x f , xx x a ⎪⎭⎫ ⎝⎛-≤⎪⎭⎫ ⎝⎛⋅≤⎪⎭⎫ ⎝⎛--41221414 ∴ x x x x a ⎪⎭⎫ ⎝⎛-⋅≤≤⎪⎭⎫ ⎝⎛-⋅-21222124在[)0,+∞上恒成立 ∴ minmax 21222124⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⋅≤≤⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⋅-x x x x a 设t x =2,t t t h 14)(--=,tt t p 12)(-=,由x ∈[)0,+∞得 t ≥1, （设121t t ≤<,()()2112121241()()0t t t t h t h t t t ---=> ()()012)()(21212121<+-=-t t t t t t t p t p所以)(t h 在[)1,+∞上递减,)(t p 在[)1,+∞上递增, （单调性不证,不扣分））)(t h 在[)1,+∞上的最大值为(1)5h =-, )(t p 在[)1,+∞上的最小值为(1)1p =所以实数a 的取值范围为[]5,1-（Ⅲ）121)(2+⋅+-=x m x g , ∵ m>0 ,[]1,0∈x ∴ ()g x 在[]0,1上递减, ∴ )0()()1(g x g g ≤≤ 即1)(11≤≤+-x g m m ∵ 01<<-m ,[]1,0∈x ∴ ()g x 在[]0,1上递增,∴ )1()()0(g x g g ≤≤ 即个m m x g +-≤≤11)(1 ①当0>m 时,111<+-mm ,1)(<x g 此时 1)(≥m T ②当0=m ,即,1)(=x g ,1)(=x g 此时 1)(≥m T , ③当01<<-m 时,m m x g +-<11)(,此时 mm m T +-≥11)( 综上所述:当0≥m 时,)(m T 的取值范围是[)+∞,1;当01<<-m 时,)(m T 的取值范围是 ⎪⎭⎫⎢⎣⎡+∞+-,11m m ． 考点：函数恒成立问题；函数最值的应用．。

分数指数幂1．下列命题中，正确命题的个数是__________． ①n a n ＝a ②若a ∈R ，则(a 2－a ＋1)0＝1 ③3x 4＋y 3＝x 43＋y ④3－5＝6(－5)22．下列根式、分数指数幂的互化中，正确的序号是__________． ①－x ＝(－x)12(x ≠0) ②x x ＝x 34 ③x －13＝－3x ④3x·4x ＝x 112⑤(x y )－34＝4(y x )3(xy ≠0) ⑥6y 2＝y 13(y<0)3．若a ＝2，b ＝3，c ＝－2，则(a c )b ＝__________.4．根式a a 的分数指数幂形式为__________．5.4(－25)2＝__________.6．2－(2k ＋1)－2－(2k －1)＋2－2k 的化简结果是__________．7．(1)设α，β是方程2x 2＋3x ＋1＝0的两个根，则(14)α＋β＝__________.(2)若10x ＝3,10y ＝4，则10x －12y ＝__________.8．(1)求下列各式的值：①2723②(614)12③(49)－32(2)解方程：①x －3＝18②x ＝914.(1)(0.027)23＋(12527)13－(279)0.5(2)(13)12＋3·(3－2)－1－(11764)14－(333)34－(13)－1.10．已知a 12＋a －12＝4，求a ＋a －1的值．(1)5x －23y 12(－14x －1y 12)(－56x 13y －16)(2)m ＋m －1＋2m －12＋m 12.12．[(－2)2]－12的值是__________．13．化简(36a 9)4·(63a 9)4的结果是__________．14．以下各式，化简正确的个数是__________．①a 25a －13a －115＝1②(a 6b －9)－23＝a －4b 6 ③(－x 14y －13)(x －12y 23)(－x 14y 23)＝y④－15a 12b 13c －3425a －12b 13c 54＝－35ac15．(2010山东德州模拟，4改编)如果a 3＝3，a 10＝384，则a 3[(a 10a 3)17]n 等于__________．16．化简3(a －b )3＋(a －2b )2的结果是__________．17．下列结论中，正确的序号是__________．①当a<0时，(a 2)32＝a 3 ②n a n ＝|a|(n>1且n ∈N *)③函数y ＝(x －2)12－(3x －7)0的定义域是(2，＋∞)④若100a ＝5,10b ＝2，则2a ＋b ＝118．(1)若a ＝(2＋3)－1，b ＝(2－3)－1，则(a ＋1)－2＋(b ＋1)－2的值是__________．(2)若x ＞0，y ＞0，且x(x ＋y)＝3y(x ＋5y)，则2x ＋2xy ＋3y x －xy ＋y的值是__________．19．已知a ＝2 0091n －2 009－1n2(n ∈N *)，则(a 2＋1＋a)n 的值是__________．20．若S ＝(1＋2－132)(1＋2－116)(1＋2－18)(1＋2－14)(1＋2－12)，那么S 等于__________．21．先化简，再求值： (1)a 2·5a 310a 7·a ，其中a ＝8－53；(2)a 3x ＋a －3xa x ＋a－x ，其中a 2x ＝5.22.(易错题)计算：(1)(235)0＋2－2·(214)－12－(0.01)0.5(2)(279)0.5＋0.1－2＋(21027)－23－3π0＋3748(3)(0.008 1)－14－[3×(78)0]－1×[81－0.25＋(338)－13]－12－10×0.02713.23．已知x 12＋x－12＝3，求x32＋x－32＋2x2＋x－2＋3的值．24．化简下列各式：(1)x －2＋y －2x －23＋y －23－x －2－y －2x －23－y －23(2)a 43－8a 13b a 23＋23ab ＋4b 23÷(1－23b a )×3a.答案与解析基础巩固1．1 ∵n a n ＝⎩⎪⎨⎪⎧a ，当n 为奇数时，|a|，当n 为偶数时，∴①不正确； ∵a ∈R ，且a 2－a ＋1＝(a －12)2＋34≠0，∴②正确； ∵x 4＋y 3为多项式，∴③不正确；④中左边为负，右边为正显然不正确．∴只有②正确．2.②⑤ ①－x ＝－x 12，∴①错； ②x x ＝(x x)12＝(x·x 12)12＝(x 32)12＝x 34，∴②对； ③x －13＝1x 13＝13x ，∴③错； ④3x·4x ＝x 13·x 14＝x 13＋14＝x 712， ∴④错；⑤(x y )－34＝(y x )34＝4(y x)3， ∴⑤对；⑥6y 2＝|y|13＝－y 13(y<0)，∴⑥错． ∴②⑤正确．3.164 (a c )b ＝a bc ＝23×(－2)＝2－6＝126＝164. 4．a 32 a a ＝a·a 12＝a1＋12＝a 32. 5．54(－25)2＝4252＝454＝5. 6．－2－(2k ＋1)∵2－(2k ＋1)－2－(2k －1)＋2－2k ＝2－2k ·2－1－2－2k ·21＋2－2k ＝(12－2＋1)·2－2k ＝－12·2－2k ＝－2－(2k ＋1)． 7．(1)8 (2)32 (1)由根与系数的关系，得α＋β＝－32，∴(14)α＋β＝(14)－32＝(2－2)－32＝23＝8. (2)∵10x ＝3,10y ＝4，∴10x －12y ＝10x ÷1012y ＝10x ÷(10y )12＝3÷412＝32. 8．解：(1)①2723＝(33)23＝33×23＝32＝9. ②(614)12＝(254)12＝[(52)2]12＝(52)2×12＝52. ③(49)－32＝(23)2×(－32)＝(23)－3＝(32)3＝278. (2)①∵x －3＝18＝2－3，∴x ＝2. ②∵x ＝914，∴(x)2＝(914)2＝912.∴x ＝(32)12＝3. 9．解：(1)原式＝(0.33)23＋(12527)13－(259)12＝9100＋53－53＝9100. (2)原式＝3－12＋33－2－(8164)14－(3－23)34－31 ＝33＋3(3＋2)－[4(34)4]14－3－12－3 ＝33＋3＋6－2·34－33－3 ＝6－342. 10．解：∵a 12＋a －12＝4.∴两边平方，得a ＋a －1＋2＝16.∴a ＋a －1＝14. 11．解：(1)原式＝245×5×x －23＋1－13×y 12－12＋16＝24x 0y 16＝24y 16； (2)原式＝(m 12)2＋2m 12·m －12＋(m －12)2m －12＋m 12＝(m 12＋m －12)2m 12＋m －12＝m 12＋m －12. 能力提升12.22 原式＝2－12＝12＝22. 13．a 4 原式＝(3a 96)4·(6a 93)4＝(a 32×13)4·(a3×16)4＝(a 12)4·(a 12)4＝a 2·a 2＝a 4. 14．3 由分数指数幂的运算法则知①②③正确；对④，∵左边＝－35a 12＋12b 13－13c －34－54＝－35a 1b 0c －2＝－35ac －2≠右边，∴④错误． 15．3·2n 原式＝3·[(3843)17]n ＝3·[(128)17]n ＝3·(27×17)n ＝3·2n . 16．b 或2a －3b 原式＝a －b ＋|a －2b|＝⎩⎪⎨⎪⎧ a －b ＋2b －a ，a ＜2b a －b ＋a －2b ，a ≥2b ＝⎩⎪⎨⎪⎧b ，a ＜2b ，2a －3b ，a ≥2b.17．④ ①中，当a ＜0时，(a 2)32＝[(a 2)12]3＝(|a|)3＝(－a)3＝－a 3， ∴①不正确；当a ＜0，n 为奇数时，n a n ＝a ， ∴②不正确；③中，有⎩⎪⎨⎪⎧ x －2≥0，3x －7≠0，即x ≥2且x ≠73，故定义域为[2，73)∪(73，＋∞)， ∴③不正确；④中，∵100a ＝5,10b ＝2，∴102a ＝5,10b ＝2,102a ×10b ＝10.∴2a ＋b ＝1.∴④正确．18．(1)23 (2)3 (1)a ＝12＋3＝2－3，b ＝12－3＝2＋3， ∴(a ＋1)－2＋(b ＋1)－2＝(3－3)－2＋(3＋3)－2＝1(3－3)2＋1(3＋3)2＝(3＋3)2＋(3－3)2(3－3)2·(3＋3)2 ＝32＋2·3·3＋3＋32－2·3·3＋3[(3－3)(3＋3)]2＝2×9＋6(9－3)2＝2436＝23. (2)由已知条件，可得(x)2－2xy －15(y)2＝0，∴x ＋3y ＝0或x －5y ＝0.∵x ＞0，y ＞0，∴x ＝5y ，x ＝25y.∴原式＝50y ＋225y 2＋3y 25y －25y 2＋y ＝50y ＋10y ＋3y 25y －5y ＋y ＝63y 21y＝3. 19．2 009 ∵a ＝2 0091n －2 009－1n 2，∴a 2＋1＝1＋2 0092n ＋2 009－2n －24＝(2 0091n )2＋2＋(2 009－1n )24＝(2 0091n ＋2 009－1n 2)2.∴a 2＋1＋a ＝2 0091n ＋2 009－1n 2＋2 0091n －2 009－1n 2＝2 0091n. ∴(a 2＋1＋a)n ＝(2 0091n)n ＝2 009. 20.12(1－2－132)－1 原式＝(1－2－132)(1＋2－132)(1＋2－116)(1＋2－18)(1＋2－14)(1＋2－12)1－2－132＝(1－2－116)(1＋2－116)(1＋2－18)(1＋2－14)(1＋2－12)1－2－132＝(1－2－18)(1＋2－18)(1＋2－14)(1＋2－12)1－2－132＝(1－2－14)(1＋2－14)(1＋2－12)1－2－132＝(1－2－12)(1＋2－12)1－2－132＝1－2－11－2－132＝12(1－2－132)－1. 21．解：(1)原式＝a2＋35－710－12＝a 75＝(8－53)75＝8－73＝(23)－73＝2－7＝1128. (2)原式＝(a x )3＋(a －x )3a x ＋a －x ＝(a x ＋a －x )(a 2x －a x ·a －x ＋a －2x )a x ＋a －x＝a 2x －1＋a －2x ＝5－1＋15＝415. 22．解：(1)原式＝1＋14·(49)12－(1100)12＝1＋14×23－(110)2×12＝1＋16－110＝1115. (2)原式＝(259)12＋(110)－2＋(6427)－23－3×1＋3748＝53＋100＋(43)－2－3＋3748＝53＋100＋916－3＋3748＝100. (3)原式＝[(0.3)4]－14－3－1×[(34)－14＋(278)－13]－12－10×[(0.3)3]13＝0.3－1－13[3－1＋(32)－1]－12－10×0.3＝103－13(13＋23)－12－3＝103－13－3＝0.23．解：∵x 12＋x －12＝3，∴(x 12＋x －12)2＝9.∴x ＋x －1＝7. ∴原式＝(x 12)3＋(x －12)3＋2x 2＋x －2＋3＝(x 12＋x －12)(x －1＋x －1)＋2(x ＋x －1)2－2＋3＝3×(7－1)＋272－2＋3＝25.- 11 -拓展探究24．解：(1)原式＝(x －23)3＋(y －23)3x －23＋y －23－(x －23)3－(y －23)3x －23－y －23＝(x －23)2－x －23·y －23＋(y －23)2－(x －23)2－x －23·y －23－(y －23)2＝－2(xy)－23. (2)原式＝a 13[(a 13)3－(2b 13)3]a 23＋2a 13b 13＋(2b 13)2÷(1－2b 13a 13)×a 13 ＝a 13(a 13－2b 13)[a 23＋2a 13b 13＋(2b 13)2]a 23＋2a 13b 13＋(2b 13)2÷a 13－2b 13a 13×a 13＝a 13(a 13－2b 13)·11×a 13a 13－2b 13×a 13＝a 13·a 13·a 13＝a.。

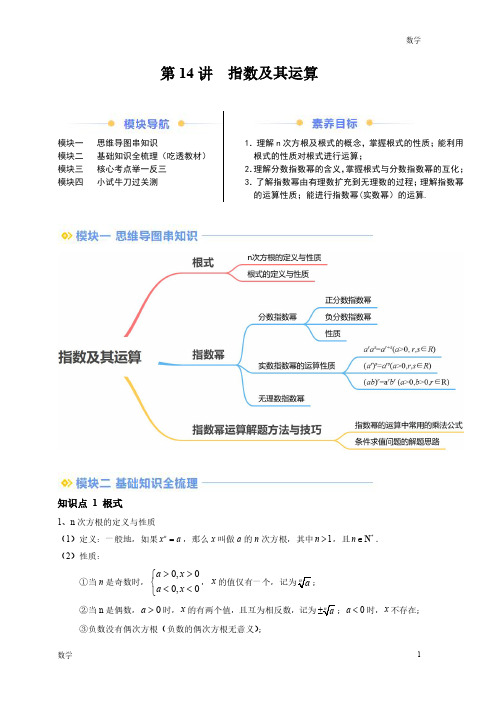
第14讲指数及其运算模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．理解n 次方根及根式的概念，掌握根式的性质；能利用根式的性质对根式进行运算；2．理解分数指数幂的含义，掌握根式与分数指数幂的互化；3．了解指数幂由有理数扩充到无理数的过程；理解指数幂的运算性质；能进行指数幂(实数幂）的运算.知识点1根式1、n 次方根的定义与性质（1）定义：一般地，如果n x a =，那么x 叫做a 的n 次方根，其中1n >，且*n ∈N ．（2）性质：①当n 是奇数时，0,00,0>>⎧⎨<<⎩a x a x ，x②当n 是偶数，0>a 时，x 的有两个值，且互为相反数，记为；0<a 时，x 不存在；③负数没有偶次方根（负数的偶次方根无意义）；④0的任何次方根都是00(,1)n N n +=∈>．2、根式的定义与性质（1n 叫做根指数，a 叫做被开方数．（2）性质：（1n >，且n *∈N）n=a；,,,.⎧⎪=⎨⎪⎩为奇数为偶数na n a n 知识点2指数幂1、分数指数幂（1）正分数指数幂：规定：mn a=()0,,,1a m n n *>∈>N （2）负分数指数幂：规定：1mn m naa-==()0,,,1a m n n *>∈>N （3）性质：0的正分数指数幂等于0，0的负分数指数幂没有意义．【要点辨析】分数指数幂的注意事项：①分数指数幂是指数概念的又一推广，分数指数幂m na 不可理解为mn个a 相乘，它是根式的一种新的写法．在这样的规定下，根式与分数指数幂是表示相同意义的量，只是形式不同而已．化成分数指数幂的形式时，不要轻易对mn进行约分．③在保证相应的根式有意义的前提下，负数也存在分数指数幂，如()235-=有意义，但()345-=就没有意义．2、实数指数幂的运算性质①(0,,)+=>∈r s r s a a a a r s R ．②()=sra rs a (0,,)a r s >∈R ．③()=r ab r r a b (0,0,)a b r >>∈R ．3、无理数指数幂一般地，无理数指数幂a α（0a >，α为无理数）是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．【注意】（1）对于无理数指数幂，我们只需要了解两点：①它是一个确定的实数；②它是有理数指数幂无限逼近的结果．（2）定义了无理数指数幂之后，幂的指数就由原来的有理数范围扩充到了实数范围．知识点3指数幂运算解题方法与技巧1、指数幂的运算中常用的乘法公式（1）完全平方公式：222()2a b a ab b -=-+；222()2a b a ab b +=++；（2）平方差公式：22()()a b a b a b -=-+；（3）立方差公式：3322()()a b a b a ab b -=-++；（4）立方和公式：3322()()a b a b a ab b +=+-+；（5）完全立方公式：33223()33a b a a b ab b -=-+-；33223()33a b a a b ab b +=+++．2、条件求值问题的解题思路（1）将条件中的式子用待求式表示出来，进而代入化简得出结论；（2）当直接代入不易时，可以从总体上把握已知式和所求式的特点，从而巧妙求解，一般先利用平方差、立方和（差）以及完全平方公式对其进行化简，再用整体代入法来求值；（3）适当应用换元法，能使公式的使用更加清晰，过程更简洁．考点一：根式的概念及辨析例1．（23-24高一上·全国·专题练习）若a 是实数，则下列式子中可能没有意义的是（）AB C D 【变式1-1】（23-24高一上·全国·课后作业）R a ∈，下列各式一定有意义的是（）A ．2a -B ．14a C ．23a D ．0a【变式1-2】（2023高一·江苏·a 的取值范围是（）A ．0a ≥B ．1a ≥C ．2a ≥D ．Ra ∈【变式1-3】（223-24高一下·贵州遵义·月考）若34(12)x --有意义，则实数x 的取值范围为考点二：利用根式的性质化简求值例2.（23-24高一上·北京·期中）下列各式正确的是（）A3=-Bx=C2=D ．01a =【变式2-1】（23-24高一上·贵州贵阳·月考）若0ab <，则化简）A ．-1B ．0C ．1D ．2【变式2-2】（23-24高一上·全国·；【变式2-3】（23-24高一上·甘肃兰州·期中）（多选）若412x<-，3的结果可能为（）A ．210x -B ．46x -C ．24x -+D ．410x --考点三：根式与分数指数幂互化例3.（23-24高一上·湖南株洲·月考）下列关于nm a -(),m n *∈N 的形式的运算正确的是（）A．538-=B．538-=C．538-=D ．()328--=【变式3-1】（23-24高一上·浙江杭州·期中）（多选）下列各式正确的是（）A ．46a=B 5=-C．(36=D ．23a -=【变式3-2】（23-24高一上·江西新余·期中）（多选）下列根式与分数指数幂的互化中正确的有（）A ．)130xx -=≠B()120aa =≥C．21320,0)x y x y ->>D ．3142(0)x x ⎤=->【变式3-3】（23-24高一上·广东广州·期中）用分数指数幂表示并计算下列各式（式中字母均正数），写出化简步骤.(2)154m⋅考点四：利用指数幂运算性质化简例4.（23-24高一上·全国·专题练习）下列等式一定成立的是（）A ．1332a a a⋅=B ．11220⋅=a a C ．329()a a =D ．111362a a a ÷=【变式4-1】（23-24高一上·广东江门·期中）102x =，103y =，则10x y +=．【变式4-2】（23-24高一上·河南·期中）若a b =()2312222a ab ---⎡⎤=⎢⎥⎣⎦.【变式4-3】（23-24高一上·江西九江·期中）化简或计算下列各式．(1)121121332a b a b ---⎛⎫ ⎪；(2)()10.52332770.02721259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭．考点五：解简单的指数方程例5.（23-24高一·全国·专题练习）方程11416x -=的解为（）A ．2B ．﹣2C ．﹣1D ．1【变式5-1】（22-23高一上·河北沧州·期中）关于x 的方程112250x x +--+=的解的个数为（）A ．0B ．1C ．2D ．4【变式5-2】（23-24高一上·北京顺义·期中）关于x 的方程422x x -=的解为．【变式5-3】（22-23高三·全国·对口高考）方程(2522xx x -+=的解为．考点六：整体换元法解决条件求值例6.（23-24高一下·辽宁抚顺·开学考试）已知12a a+=，则1122a a -+等于（）A ．2B ．4C ．2±D ．4±【变式6-1】（23-24高一上·全国·专题练习）已知11223a a -+=，则33221122a a a a--++的值为．【变式6-2】（23-24高一上·全国·专题练习）已知11223x x-+=，计算：22111227x x x x x x---+-+++.【变式6-3】（23-24高一上·湖南娄底·期末）已知11223a a -+=，求下列各式的值：(1)1a a -+；(2)33222232a a a a --+-+-．一、单选题1．（23-24高一上·青海海南·期中）已知R a ∈，则下列各式一定有意义的是（）A ．2a -B ．13a C ．12a D ．0a 2．（23-24高一上·陕西咸阳·期末）化简32的结果为（）A ．5BC ．5-D．3．（23-24高一上·北京大兴·月考）已知0a >=（）A ．12a B ．32a C ．2a D ．3a 4．（23-24高一上·安徽淮南·月考）下列根式与分数指数幂的互化错误的是（）A()120a a =>B．)340xx -=>C．)21320,0x y x y -=>>D ．()32140x x =>5．（23-24高一上·江苏泰州·期中）已知14x x -+=，则22x x -+等于（）A ．6B ．12C ．14D ．166．（23-24高一上·四川德阳·月考）010.256371.586-⎛⎫⨯-++= ⎪⎝⎭（）A ．110B ．109C ．108D ．100二、多选题7．（23-24高一上·四川成都·期中）以下运算结果等于2的是（）AB ．C ．D 8．（23-24高一上·浙江·月考）已知0a >，0b >，则下列各式正确的是（）A π3=-B1=C．mna-=D ．121133332463b ab a b ---⎛⎫÷-=- ⎪⎝⎭三、填空题9．（22-23高一上·上海奉贤·期末）化简()222a b ⋅=（其中0a >，0b >）．10．（23-24高一上·全国·单元测试）方程2129240x x +-⋅+=的解集是．11．（23-24高一上·重庆沙坪坝·期中）已知12102α-=，131032β=，则314210βα+=（填数值）四、解答题12．（23-24高一上·安徽马鞍山·期中）化简求值：(1)()120120.344⎛⎫+ ⎪⎝⎭(2)20.5231103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭；13．（23-24高一上·辽宁丹东·期中）已知正实数a 满足11221a a --=.(1)求1a a -+的值；(2)求33221122a a a a---+的值.第14讲指数及其运算模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．理解n 次方根及根式的概念，掌握根式的性质；能利用根式的性质对根式进行运算；2．理解分数指数幂的含义，掌握根式与分数指数幂的互化；3．了解指数幂由有理数扩充到无理数的过程；理解指数幂的运算性质；能进行指数幂(实数幂）的运算.知识点1根式1、n 次方根的定义与性质（1）定义：一般地，如果n x a =，那么x 叫做a 的n 次方根，其中1n >，且*n ∈N ．（2）性质：①当n 是奇数时，0,00,0>>⎧⎨<<⎩a x a x ，x②当n 是偶数，0>a 时，x 的有两个值，且互为相反数，记为；0<a 时，x 不存在；③负数没有偶次方根（负数的偶次方根无意义）；④0的任何次方根都是00(,1)n N n +=∈>．2、根式的定义与性质（1n 叫做根指数，a 叫做被开方数．（2）性质：（1n >，且n *∈N）n=a；,,,.⎧⎪=⎨⎪⎩为奇数为偶数na n a n 知识点2指数幂1、分数指数幂（1）正分数指数幂：规定：mn a=()0,,,1a m n n *>∈>N （2）负分数指数幂：规定：1mn m naa-==()0,,,1a m n n *>∈>N （3）性质：0的正分数指数幂等于0，0的负分数指数幂没有意义．【要点辨析】分数指数幂的注意事项：①分数指数幂是指数概念的又一推广，分数指数幂m na 不可理解为mn个a 相乘，它是根式的一种新的写法．在这样的规定下，根式与分数指数幂是表示相同意义的量，只是形式不同而已．化成分数指数幂的形式时，不要轻易对mn进行约分．③在保证相应的根式有意义的前提下，负数也存在分数指数幂，如()235-=有意义，但()345-=就没有意义．2、实数指数幂的运算性质①(0,,)+=>∈r s r s a a a a r s R ．②()=sra rs a (0,,)a r s >∈R ．③()=r ab r r a b (0,0,)a b r >>∈R ．3、无理数指数幂一般地，无理数指数幂a α（0a >，α为无理数）是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．【注意】（1）对于无理数指数幂，我们只需要了解两点：①它是一个确定的实数；②它是有理数指数幂无限逼近的结果．（2）定义了无理数指数幂之后，幂的指数就由原来的有理数范围扩充到了实数范围．知识点3指数幂运算解题方法与技巧1、指数幂的运算中常用的乘法公式（1）完全平方公式：222()2a b a ab b -=-+；222()2a b a ab b +=++；（2）平方差公式：22()()a b a b a b -=-+；（3）立方差公式：3322()()a b a b a ab b -=-++；（4）立方和公式：3322()()a b a b a ab b +=+-+；（5）完全立方公式：33223()33a b a a b ab b -=-+-；33223()33a b a a b ab b +=+++．2、条件求值问题的解题思路（1）将条件中的式子用待求式表示出来，进而代入化简得出结论；（2）当直接代入不易时，可以从总体上把握已知式和所求式的特点，从而巧妙求解，一般先利用平方差、立方和（差）以及完全平方公式对其进行化简，再用整体代入法来求值；（3）适当应用换元法，能使公式的使用更加清晰，过程更简洁．考点一：根式的概念及辨析例1．（23-24高一上·全国·专题练习）若a 是实数，则下列式子中可能没有意义的是（）AB C D 【答案】D【解析】A.R a ∈有意义；B.R a ∈有意义；C.R a ∈有意义；D.a<0无意义；故选：D【变式1-1】（23-24高一上·全国·课后作业）R a ∈，下列各式一定有意义的是（）A ．2a -B ．14a C ．23a D ．0a 【答案】C【解析】对于A ，当0a =时，2a -无意义，A 不是；对于B ，当a<0时，14a 无意义，B 不是；对于C ，23a =C 是；对于D ，当0a =时，0a 无意义，D 不是.故选：C【变式1-2】（2023高一·江苏·a 的取值范围是（）A ．0a ≥B ．1a ≥C ．2a ≥D ．Ra ∈【答案】B102R a a -≥⎧⎨-∈⎩，解得1a ≥，所以a 的取值范围是1a ≥.故选：B【变式1-3】（223-24高一下·贵州遵义·月考）若34(12)x --有意义，则实数x 的取值范围为【答案】1(,2-∞【解析】由34(12)x --120x ->，解得12x <，故答案为：1(,2-∞．考点二：利用根式的性质化简求值例2.（23-24高一上·北京·期中）下列各式正确的是（）A3=-B x =C 2=D ．01a =【答案】C【解析】A 3=，故A 错误；B x =，故B 错误；C2=，故C 正确；D ：01a =，当0a ≠时成立，故D 错误；故选：C.【变式2-1】（23-24高一上·贵州贵阳·月考）若0ab <，则化简）A ．-1B ．0C ．1D ．2【答案】B【解析】+==a b a b ⎛=+ ⎝因为0ab <，所以,a b 异号，0a b a b +=，所以0a b a b a b a b a b++==，所以，0+=.故选：B.【变式2-2】（23-24高一上·全国·；【答案】6-=6(446-++=-．【变式2-3】（23-24高一上·甘肃兰州·期中）（多选）若412x<-，3的结果可能为（）A ．210x -B ．46x -C ．24x -+D ．410x --【答案】AC 【解析】由题意知412x <-，即4102x-<-，即202x x +>-，故(2)(2)0,2x x x +->∴<-或2x >，3|2|3x =+-3523210,23523352324,2x x x x x x x x x x ----=->⎧=--+-=⎨-+++-=-+<-⎩，故选：AC考点三：根式与分数指数幂互化例3.（23-24高一上·湖南株洲·月考）下列关于nm a -(),m n *∈N 的形式的运算正确的是（）A．538-=B．538-=C．538-=D ．()328--=【答案】A【解析】由于5353818-==，A 正确，B ，C 错误；()328--=D 错误，故选：A【变式3-1】（23-24高一上·浙江杭州·期中）（多选）下列各式正确的是（）A ．46a=B 5=-C．(36=D ．23a -=【答案】AC【解析】对于A：4263a a ==A正确；对于B 5=，故B 错误；对于C：(2636===，故C 正确；对于D：23231aa-==D 错误.故选：AC【变式3-2】（23-24高一上·江西新余·期中）（多选）下列根式与分数指数幂的互化中正确的有（）A ．)130xx -=≠B()120a a =≥C．21320,0)x y x y ->>D ．3142(0)x x ⎤=->【答案】BC【解析】对选项A：)130xx -=≠，错误；对选项B()1313220a a a ⎛⎫==≥ ⎪⎝⎭，正确；对选项C22133212(0,0)y x y x y x-==>>，正确；对选项D ：33214432(0)x x x ⎛⎫==> ⎪⎝⎭，错误；故选：BC【变式3-3】（23-24高一上·广东广州·期中）用分数指数幂表示并计算下列各式（式中字母均正数），写出化简步骤.(2)154m⋅【答案】(1)14b ；(2)1【解析】（1111224b b ⎛⎫=== ⎪⎝⎭.（2）154m⋅111115324023651641m m m mm m m-⋅⋅====⋅.考点四：利用指数幂运算性质化简例4.（23-24高一上·全国·专题练习）下列等式一定成立的是（）A ．1332a a a ⋅=B ．11220⋅=a a C ．329()a a =D ．111362a a a ÷=【答案】D【解析】对于A ：11311333262a a a a +⋅==，故A 错误；对于B ：11212221+⋅==a a a a ，故B 错误；对于C ：326()a a =，故C 错误；对于D ：1111132362a a a a -÷==，故D 正确；故选：D【变式4-1】（23-24高一上·广东江门·期中）102x =，103y =，则10x y +=．【答案】6【解析】102x =Q ，103y =，101010236x y x y +∴=⋅=⨯=，故答案为：6．【变式4-2】（23-24高一上·河南·期中）若a b =()2312222a ab ---⎡⎤=⎢⎥⎣⎦.【答案】1【解析】由题意，0,0a b >>，所以()()231222232246a b ab a b a b -----⎡==⎤⎢⎥⎣⎦，又11322,2a b --===，所以原式6411223222221----⎛⎫⎛⎫=⋅=⋅= ⎪ ⎪⎝⎭⎝⎭.故答案为：1.【变式4-3】（23-24高一上·江西九江·期中）化简或计算下列各式．(1)121121332a b a b ---⎛⎫ ⎪；(2)()10.52332770.02721259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭．【答案】(1)1a；(2)0.09【解析】（1）原式2111111111532322132623615661ab a baba aa b⎛⎫--⎪⎝⎭-+--⋅====.（2）原式22333273550.0910001033⨯⎛⎫⎛⎫==+-= ⎪⎪⎝⎭⎝⎭.考点五：解简单的指数方程例5.（23-24高一·全国·专题练习）方程11416x -=的解为（）A ．2B ．﹣2C ．﹣1D ．1【答案】C 【解析】∵1214416x --==，∴x ﹣1＝﹣2，∴x ＝﹣1．故选：C ．【变式5-1】（22-23高一上·河北沧州·期中）关于x 的方程112250x x +--+=的解的个数为（）A ．0B ．1C ．2D ．4【答案】B【解析】解：原方程即222502x x ⨯-+=，化简可得()2225220x x ⨯+⨯-=，令2(0)x t t =>，可得22520t t +-=，该方程有且只有一个正根，由于2x t =单调递增，所以t 与x 一一对应，即原方程只有一个解.故选：B .【变式5-2】（23-24高一上·北京顺义·期中）关于x 的方程422x x -=的解为．【答案】1x =【解析】由422x x -=可得()22220x x --=，即()()21220x x+-=，因为20x >，可得22x =，故1x =.所以，方程关于x 的方程422x x -=的解为1x =.故答案为：1x =.【变式5-3】（22-23高三·全国·对口高考）方程(2522xx x -+=的解为．【答案】5x =或12x =【解析】由题意可得(2599222222xxx x x -+⎛⎫=== ⎪⎝⎭，所以25922x x x -+=，即221150x x -+=，解得5x =或12x =，故答案为：5x =或12x =考点六：整体换元法解决条件求值例6.（23-24高一下·辽宁抚顺·开学考试）已知12a a+=，则1122a a -+等于（）A ．2B ．4C ．2±D ．4±【答案】A【解析】112221()2224a a a a-+=++=+=，所以11222a a -+=.故选：A.【变式6-1】（23-24高一上·全国·专题练习）已知11223a a -+=，则33221122a a a a--++的值为．【答案】6【解析】因为11223a a-+=，所以2112223a a -⎛⎫+= ⎪⎝⎭，即129a a -++=，所以17a a -+=，所以3333112222a aa a --⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭22111111222222a a a a a a ---⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=+-⋅+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()()11122371181a a a a --⎛⎫=++=⨯- ⎝-=⎪⎭，所以332211221863a a a a--+==+．【变式6-2】（23-24高一上·全国·专题练习）已知11223x x -+=，计算：22111227x x x x x x---+-+++.【答案】4【解析】因为11223x x-+=，所以211229x x -⎛⎫+= ⎪⎝⎭，所以129x x -++=，所以17x x -+=，所以()2127x x -+=，即22249x x -++=，所以2247x x -+=，所以22111227477473x x x x x x---+--==++++.【变式6-3】（23-24高一上·湖南娄底·期末）已知11223a a -+=，求下列各式的值：(1)1a a -+；(2)33222232a a a a --+-+-．【答案】(1)7；(2)13【解析】（1）由题意11223a a-+=，所以21112222327a a a a --⎛⎫+=+-=-= ⎪⎝⎭.（2）由题意11223a a -+=，所以()()1111212233222222213371331512744534a a a a a a a a a a a a ------⎛⎫⎛⎫- ⎪⎪⨯--+-⎝⎭⋅⎝⎭==-==+--+++-.一、单选题1．（23-24高一上·青海海南·期中）已知R a ∈，则下列各式一定有意义的是（）A ．2a -B ．13a C ．12a D ．0a 【答案】B【解析】对于A ，由221aa -=可知，0a =时表达式无意义；对于B ，根据幂函数性质可知，R a ∈时，表达式13a 恒有意义；对于C，易知12a =a<0时，表达式无意义；对于D ，当0a =时，0a 无意义；故选：B2．（23-24高一上·陕西咸阳·期末）化简32的结果为（）A ．5BC ．5-D．【答案】A【解析】332232232332555⨯⎛⎫=== ⎪⎝⎭=，故选：A3．（23-24高一上·北京大兴·月考）已知0a >=（）A ．12a B ．32a C ．2a D ．3a 【答案】A12a =，故选：A4．（23-24高一上·安徽淮南·月考改编）下列根式与分数指数幂的互化错误的是（）A()120aa =>B．)340xx -=>C．)21320,0x y x y -=>>D ．()32140x x =>【答案】B【解析】对于A()1313220a a a ⎛⎫==> ⎪⎝⎭，故A 正确；对于B选项，)334410xx x -⎛⎫=> ⎪⎝⎭，故B 错误；对于C，)21321210,0x y x y x-=>>，故C 正确；对于D，)()33321444320x x x ⎛⎫⎤===> ⎪⎝⎭，故D 正确．故选：B ．5．（23-24高一上·江苏泰州·期中）已知14x x -+=，则22x x -+等于（）A ．6B ．12C ．14D ．16【答案】C【解析】由14x x -+=可得：()2122216x x x x --+=++=，则2214x x -+=.故选：C.6．（23-24高一上·四川德阳·月考）010.256371.586-⎛⎫⨯-++= ⎪⎝⎭（）A ．110B ．109C ．108D ．100【答案】A【解析】原式()11133333112344131442222223221083331210810231-⎛⎫=+=+= ⎪⎝⎭⎛⎫⎛⎫⎛⎫⨯+⨯+⨯-=⨯+- ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选：A.二、多选题7．（23-24高一上·四川成都·期中）以下运算结果等于2的是（）A B ．C ．D 【答案】BCD【解析】对于A π44π=-=-，不合题意；对于B ，2=，符合题意；对于C ，()22=--=，符合题意；对于D 22=-=，符合题意.故选：BCD8．（23-24高一上·浙江·月考）已知0a >，0b >，则下列各式正确的是（）A π3=-B 1=C ．mna-=D ．121133332463b ab a b ---⎛⎫÷-=- ⎪⎝⎭【答案】ABD【解析】A 选项：由π30->π3=-，A 选项正确；B ()11111123612312600222221a b b a ab a b ⎛⎫⎛⎫-⨯-+⨯ ⎪ ⎪--⎝⎭⎝⎭⎡⎤====⎢⎥⎣⎦，B 选项正确；C 选项：m na-C 选项错误；D 选项：112121101333333331246663b ab a a b a b b ⎛⎫⎛⎫------- ⎪ ⎪⎝⎭⎝⎭⎛⎫÷-=-=-=- ⎪⎝⎭，D 选项正确；故选：ABD.三、填空题9．（22-23高一上·上海奉贤·期末）化简()222a b ⋅=（其中0a >，0b >）．【答案】4ab【解析】()((4222222a b ab a b +-⋅=⋅=.故答案为：4ab .10．（23-24高一上·全国·单元测试）方程2129240x x +-⋅+=的解集是．【答案】{1,2}-【解析】令2x t =，则0t >，方程可化为22940t t -+=，解得12t =或4t =，所以，122x =或24x =，解得=1x -或2x =.所以，方程的解集为{1,2}-.故答案为：{1,2}-.11．（23-24高一上·重庆沙坪坝·期中）已知12102α-=，131032β=，则314210βα+=（填数值）【答案】2【解析】()()31131113113142513422342242101010=322222αβα⎛⎫⎛⎫⨯⨯+-⨯+- ⎪⎝⎭⎝⎭⎛⎫⎛⎫=⨯⨯=== ⎪ ⎪⎝⎭⎝⎭.故答案为：2四、解答题12．（23-24高一上·安徽马鞍山·期中）化简求值：(1)()120120.344⎛⎫+ ⎪⎝⎭(2)20.52031103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭；【答案】(1)52；(2)0【解析】（1）()120120.344⎛⎫+ ⎪⎝⎭1293511422⎛⎫=+=+= ⎪⎝⎭.（2）20.52031103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222364493322220273444-⎛⎫⎛⎫⎛⎫⎛⎫⨯-÷=-⨯-⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭13．（23-24高一上·辽宁丹东·期中）已知正实数a 满足11221a a --=.(1)求1a a -+的值；(2)求33221122a a a a ---+的值.【答案】(1)3；(2)5【解析】（1）将11221a a --=两边平方得121a a -+-=，所以13a a -+=.（2）因为a 是正实数，令1122(0)a a x x -+=>，则2125x a a -=++=，所以x 可得()33111222214a a a a a a ---⎛⎫-=-++= ⎪⎝⎭，所以332211225a a a a ---==+.。

初中数学分数指数幂练习题（含解析）分数指数幂1．下列命题中，正确命题的个数是__________．①n a n ＝a ②若a ∈R ，则(a 2－a ＋1)0＝1 ③3x 4＋y 3＝x 43＋y ④3－5＝6(－5)22．下列根式、分数指数幂的互化中，正确的序号是__________．①－x ＝(－x)12(x ≠0) ②x x ＝x 34 ③x －13＝－3x④3x·4x ＝x 112⑤(x y )－34＝4(y x )3(xy ≠0) ⑥6y 2＝y 13(y<0)3．若a ＝2，b ＝3，c ＝－2，则(a c )b ＝__________.4．根式a a 的分数指数幂形式为__________．5.4(－25)2＝__________.6．2－(2k ＋1)－2－(2k －1)＋2－2k 的化简结果是__________．7．(1)设α，β是方程2x 2＋3x ＋1＝0的两个根，则(14)α＋β＝__________.(2)若10x ＝3,10y ＝4，则10x －12y ＝__________.8．(1)求下列各式的值：①2723②(614)12③(49)－32(2)解方程：①x －3＝18②x ＝914.(1)(0.027)23＋(12527)13－(279)0.5(2)(13)12＋3·(3－2)－1－(11764)14－(333)34－(13)－1.10．已知a 12＋a －12＝4，求a ＋a －1的值．(1)5x －23y 12(－14x －1y 12)(－56x 13y －16)(2)m ＋m －1＋2m －12＋m 12.12．[(－2)2]－12的值是__________．13．化简(36a 9)4·(63a 9)4的结果是__________．14．以下各式，化简正确的个数是__________．①a 25a －13a －115＝1②(a 6b －9)－23＝a －4b 6 ③(－x 14y －13)(x －12y 23)(－x 14y 23)＝y④－15a 12b 13c －3425a －12b 13c 54＝－35ac15．(2010山东德州模拟，4改编)如果a 3＝3，a 10＝384，则a 3[(a 10a 3)17]n 等于__________．16．化简3(a －b )3＋(a －2b )2的结果是__________．17．下列结论中，正确的序号是__________．①当a<0时，(a 2)32＝a 3 ②n a n ＝|a|(n>1且n ∈N *)③函数y ＝(x －2)12－(3x －7)0的定义域是(2，＋∞)④若100a ＝5,10b ＝2，则2a ＋b ＝118．(1)若a ＝(2＋3)－1，b ＝(2－3)－1，则(a ＋1)－2＋(b ＋1)－2的值是__________．(2)若x ＞0，y ＞0，且x(x ＋y)＝3y(x ＋5y)，则2x ＋2xy ＋3y x －xy ＋y的值是__________．19．已知a ＝2 0091n －2 009－1n2(n ∈N *)，则(a 2＋1＋a)n 的值是__________．20．若S ＝(1＋2－132)(1＋2－116)(1＋2－18)(1＋2－14)(1＋2－12)，那么S 等于__________．21．先化简，再求值： (1)a 2·5a 310a 7·a ，其中a ＝8－53；(2)a 3x ＋a －3xa x ＋a－x ，其中a 2x ＝5.22.(易错题)计算：(1)(235)0＋2－2·(214)－12－(0.01)0.5(2)(279)0.5＋0.1－2＋(21027)－23－3π0＋3748(3)(0.008 1)－14－[3×(78)0]－1×[81－0.25＋(3 38)－13]－12－10×0.02713.23．已知x 12＋x－12＝3，求x32＋x－32＋2x2＋x－2＋3的值．24．化简下列各式：(1)x －2＋y －2x －23＋y －23－x －2－y －2x －23－y －23(2)a 43－8a 13b a 23＋23ab ＋4b 23÷(1－23b a )×3a.答案与解析基础巩固1．1 ∵n a n ＝a ，当n 为奇数时，|a|，当n 为偶数时，∴①不正确；∵a ∈R ，且a 2－a ＋1＝(a －12)2＋34≠0，∴②正确；∵x 4＋y 3为多项式，∴③不正确；④中左边为负，右边为正显然不正确．∴只有②正确．2.②⑤ ①－x ＝－x 12，∴①错；②x x ＝(x x)12＝(x·x 12)12＝(x 32)12＝x 34，∴②对；③x －13＝1x 13＝13x ，∴③错；④3x·4x ＝x 13·x14＝x 13＋14＝x 712，∴④错；⑤(x y )－34＝(y x )34＝4(y x)3，∴⑤对；⑥6y 2＝|y|13＝－y 13(y<0)，∴⑥错．∴②⑤正确．3.164 (a c )b ＝a bc ＝23×(－2)＝2－6＝126＝164. 4．a 32 a a ＝a·a 12＝a1＋12＝a 32. 5．54(－25)2＝4252＝454＝5. 6．－2－(2k ＋1)∵2－(2k ＋1)－2－(2k －1)＋2－2k ＝2－2k ·2－1－2－2k ·21＋2－2k ＝(12－2＋1)·2－2k ＝－12·2－2k ＝－2－(2k ＋1)． 7．(1)8 (2)32 (1)由根与系数的关系，得α＋β＝－32，∴(14)α＋β＝(14)－32＝(2－2)－32＝23＝8. (2)∵10x ＝3,10y ＝4，∴10x －12y ＝10x ÷1012y ＝10x ÷(10y )12＝3÷412＝32. 8．解：(1)①2723＝(33)23＝33×23＝32＝9. ②(614)12＝(254)12＝[(52)2]12＝(52)2×12＝52. ③(49)－32＝(23)2×(－32)＝(23)－3＝(32)3＝278. (2)①∵x －3＝18＝2－3，∴x ＝2. ②∵x ＝914，∴(x)2＝(914)2＝912.∴x ＝(32)12＝3. 9．解：(1)原式＝(0.33)23＋(12527)13－(259)12＝9100＋53－53＝9100. (2)原式＝3－12＋33－2－(8164)14－(3－23)34－31 ＝33＋3(3＋2)－[4(34)4]14－3－12－3 ＝33＋3＋6－2·34－33 －3 ＝6－342. 10．解：∵a 12＋a －12＝4.∴两边平方，得a ＋a －1＋2＝16.∴a ＋a －1＝14. 11．解：(1)原式＝245×5×x －23＋1－13×y 12－12＋16＝24x 0y 16＝24y 16；(2)原式＝(m 12)2＋2m 12·m －12＋(m －12)2m －12＋m 12＝(m 12＋m －12)2m 12＋m －12＝m 12＋m －12. 能力提升12.22 原式＝2－12＝12＝22. 13．a 4 原式＝(3a 96)4·(6a 93)4＝(a 32×13)4·(a3×16)4＝(a 12)4·(a 12)4＝a 2·a 2＝a 4. 14．3 由分数指数幂的运算法则知①②③正确；对④，∵左边＝－35a 12＋12b 13－13c －34－54＝－35a 1b 0c －2＝－35ac －2≠右边，∴④错误．15．3·2n 原式＝3·[(3843)17]n ＝3·[(128)17]n ＝3·(27×17)n ＝3·2n . 16．b 或2a －3b 原式＝a －b ＋|a －2b|＝ a －b ＋2b －a ，a ＜2b a －b ＋a －2b ，a ≥2b ＝b ，a ＜2b ，2a －3b ，a ≥2b.17．④ ①中，当a ＜0时，(a 2)32＝[(a 2)12]3＝(|a|)3＝(－a)3＝－a 3，∴①不正确；当a ＜0，n 为奇数时，n a n ＝a ，∴②不正确；③中，有?x －2≥0，3x －7≠0，即x ≥2且x ≠73，故定义域为[2，73)∪(73，＋∞)，∴③不正确；④中，∵100a ＝5,10b ＝2，∴102a ＝5,10b ＝2,102a ×10b ＝10.∴2a ＋b ＝1.∴④正确．18．(1)23 (2)3 (1)a ＝12＋3＝2－3，b ＝12－3＝2＋3，∴(a ＋1)－2＋(b ＋1)－2＝(3－3)－2＋(3＋3)－2＝1(3－3)2＋1(3＋3)2＝(3＋3)2＋(3－3)2(3－3)2·(3＋3)2 ＝32＋2·3·3＋3＋32－2·3·3＋3[(3－3)(3＋3)]2 ＝2×9＋6(9－3)2＝2436＝23. (2)由已知条件，可得(x)2－2xy －15(y)2＝0，∴x ＋3y ＝0或x －5y ＝0.∵x ＞0，y ＞0，∴x ＝5y ，x ＝25y.∴原式＝50y ＋225y 2＋3y 25y －25y 2＋y ＝50y ＋10y ＋3y 25y －5y ＋y ＝63y 21y＝3. 19．2 009 ∵a ＝2 0091n －2 009－1n 2，∴a 2＋1＝1＋2 0092n ＋2 009－2n －24＝(2 0091n )2＋2＋(2 009－1n )24＝(2 0091n ＋2 009－1n 2 )2.∴a 2＋1＋a ＝2 0091n ＋2 009－1n 2＋2 0091n －2 009－1n 2＝2 0091n. ∴(a 2＋1＋a)n ＝(2 0091n)n ＝2 009. 20.12(1－2－132)－1 原式＝(1－2－132)(1＋2－132)(1＋2－116)(1＋2－18)(1＋2－14)(1＋2－12)1－2－132＝(1－2－116)(1＋2－116)(1＋2－18)(1＋2－14)(1＋2－12)1－2－132＝(1－2－18)(1＋2－18)(1＋2－14)(1＋2－12)1－2－132＝(1－2－14)(1＋2－14)(1＋2－12)1－2－132＝(1－2－12)(1＋2－12)1－2－132＝1－2－11－2－132＝12(1－2－132)－1. 21．解：(1)原式＝a2＋35－710－12＝a 75＝(8－53)75＝8－73＝(23)－73＝2－7＝1128. (2)原式＝(a x )3＋(a －x )3a x ＋a －x ＝(a x ＋a －x )(a 2x －a x ·a －x ＋a －2x )a x ＋a －x＝a 2x －1＋a －2x ＝5－1＋15＝415. 22．解：(1)原式＝1＋14·(49)12－(1100)12＝1＋14×23－(110)2×12＝1＋16－110＝1115. (2)原式＝(259)12＋(110)－2＋(6427)－23－3×1＋3748＝53＋100＋(43)－2－3＋3748＝53＋100＋916－3＋3748＝100. (3)原式＝[(0.3)4]－14－3－1×[(34)－14＋(278)－13]－12－10×[(0.3)3]13＝0.3－1－13[3－1＋(32)－1]－12－10×0.3＝103－13(13＋23)－12－3＝103－13－3＝0.23．解：∵x 12＋x －12＝3，∴(x 12＋x －12)2＝9.∴x ＋x －1＝7. ∴原式＝(x 12)3＋(x －12)3＋2x 2＋x －2＋3＝(x 12＋x －12)(x －1＋x －1)＋2(x ＋x －1)2－2＋3＝3×(7－1)＋272－2＋3＝25.拓展探究24．解：(1)原式＝(x －23)3＋(y －23)3x －23＋y －23－(x －23)3－(y －23)3x －23－y －23＝(x －23)2－x －23·y －23＋(y －23)2－(x －23)2－x －23·y －23－(y －23)2＝－2(xy)－23. (2)原式＝a 13[(a 13)3－(2b 13)3]a 23＋2a 13b 13＋(2b 13)2÷(1－2b 13a 13)×a 13 ＝a 13(a 13－2b 13)[a 23＋2a 13b 13＋(2b 13)2]a 23＋2a 13b 13＋(2b 13)2÷a 13－2b 13a 13×a 13＝a 13(a 13－2b 13)·11×a 13a 13－2b 13×a 13＝a 13·a 13·a 13＝a.。

2020-2021学年高中数学新教材人教A版必修第一册学案：4.1.1 n次方根与分数指数幂含解析第四章指数函数与对数函数4.1指数【素养目标】1．弄清（na）n与错误!的区别,掌握n次方根的运算．(数学抽象）2．能够利用a错误!＝错误!进行根式与分数指数幂的互化．(数学运算)3．通过对根指数n的讨论学会运用分类讨论的思想方法．(逻辑推理)【学法解读】本节的重点是根式与分数指数幂的概念及性质和分数指数幂的运算法则，以及法则的推广，这同时也是简化计算的一个方面．在学习中应采用类比的方法经历从整数指数幂到有理数指数幂、再到实数指数幂的拓展过程，掌握指数幂的运算性质．4。

1.1n次方根与分数指数幂必备知识·探新知基础知识知识点1n次方根定义一般地，如果x n＝a，那么x叫做a的__n次方根__，其中n＞1，且n∈N*个数n是奇数a＞0x＞0x仅有一个值，记为错误!a＜0x＜0n是偶数a＞0x有两个值，且互为相反数，记为±错误!a＜0x不存在思考1：正数a的n次方根一定有两个吗?提示：不一定．当n为偶数时，正数a的n次方根有两个，且互为相反数,当n为奇数时,正数a的n次方根只有一个且仍为正数．知识点2根式(1）定义:式子__错误!__叫做根式，这里n叫做__根指数__，a 叫做__被开方数__.（2）性质：(n＞1，且n∈N*）①（na）n＝a。

②n，a n＝错误!思考2：(n，a）n与错误!中的字母a的取值范围是否一样？提示：取值范围不同．式子(错误!）n中隐含a是有意义的，若n 为偶数，则a≥0，若n为奇数，a∈R；式子错误!中，a∈R.知识点3分数指数幂的意义(a〉0，m,n∈N*,且n〉1)正分数指数幂a错误!＝错误!负分数指数幂a－错误!＝错误!＝错误!0的分数指数幂0的正分数指数幂等于0,0的负分数指数幂没有意义思考3:为什么分数指数幂的底数规定a>0?提示：（1)当a<0时，若n为偶数，m为奇数,则a错误!，a－错误!无意义；（2）当a＝0时，a0无意义．知识点4有理数指数幂的运算性质(a>0，b>0，r,s∈Q）(1）a r a s＝a r＋s.（2)（a r)s＝a rs.(3)（ab)r＝a r b r。

根式与分数指数幂的互化公式在初中数学学习中，我们经常会接触到关于根式与分数指数幂的互化公式。

这个公式在代数中具有非常重要的作用，能够方便我们进行运算和推导。

下面，就让我们来详细了解一下这个公式及其应用。

首先，我们需要明确一些基础概念。

根式是一个含有根号的式子，例如√2、∛3等。

而分数指数幂则是指数为分数的幂运算，例如2的1/2次方（即根号下2）、3的2/3次方等。

它们之间通过互化公式建立起了数学上的关系。

对于根式来说，我们经常需要将其转化为分数指数幂的形式，可以使用以下互化公式：√a = a的1/2次方∛a = a的1/3次方由此可见，任何一个根式都可以用分数指数幂来表示，并且我们可以通过指数的大小关系，对根式进行大小比较。

与此同时，对于分数指数幂，我们也可以利用互化公式将其转化为根式的形式，具体公式如下：a的分数次方 = 分母根号下a的分子次方例如：2的1/2次方= √23的2/3次方 = 3的1/3次方的平方根 = ∛3的2次方= √(√3) 通过这些互化公式的使用，我们可以方便地将根式和分数指数幂进行相互转化，并且可以将它们运用到各种代数运算中，例如加减、乘除等都可以利用互化公式进行简化。

除此之外，根式与分数指数幂的互化公式在平面几何和立体几何中也有非常广泛的应用，例如在构造三角形和正方体等图形时，经常需要将根式转化为分数指数幂的形式，从而方便计算。

而在解题过程中，我们也可以利用互化公式进行代数化简，找到已知条件与问题之间的联系。

总的来说，根式与分数指数幂的互化公式是数学学习中非常重要的一个知识点，它不仅能够帮助我们简化复杂的式子，还可以在实际问题中发挥重要的作用。

因此，在学习中一定要重视这个知识点，掌握互化公式的运用方法，以便更好地应用于数学实践中。

高一数学指、对与幂基本运算练习题【重难点知识点网络】：【重难点题型突破】： 一、指数运算 1、 根式与分数指数幂(1)、性质：(na )n＝a (a 使na 有意义)；当n 为奇数时，n a n ＝a ，当n 为偶数时，na n ＝|a |＝⎩⎪⎨⎪⎧a ，a ≥0，－a ，a <0.(2)、规定：正数的正分数指数幂的意义是a m n ＝na m (a >0，m ，n ∈N *，且n >1)；正数的负分数指数幂的意义是a －mn ＝1n a m(a >0，m ，n ∈N *，且n >1)；0的正分数指数幂等于0；0的负分数指数幂没有意义.(3)、有理指数幂的运算性质：a r a s ＝a r +s ；(a r )s ＝a rs ；(ab )r ＝a r b r ，其中a >0，b >0，r ，s ∈Q. 例1、(1)、（2022·山东枣庄·高一期中）下列根式与分数指数幂的互化，正确的是（ ） A．21()x =- B12y =C．310)x x -=≠ D ．1432](0)x x =>(2)、（2022·湖南·长沙市同升湖高级中学有限公司高一期中））A ．2B ．532 C ．562D ．762(3)、（2022·黑龙江省饶河县高级中学高一阶段练习）已知16a a -+=，则1122a a --的值为（ ） A ．2B ．－2 C．±D ．±2【变式训练1-1】、（2022·湖北·恩施市第一中学高一阶段练习） ） A ．25a - B ．56a -C ．56()a -D ．56()a --【变式训练1-2】、（2022·上海·高一专题练习）已知11224x x -+=，则1x x -+=_______.【变式训练1-3】、（2022·上海市松江二中高一期中）0)a >化成有理数指数幂的形式为______.例2．（2022·江苏·常州市正行中学高一阶段练习）（1）计算：()1020.52312220.0154--⎛⎫⎛⎫+⨯- ⎪⎪⎝⎭⎝⎭；（20)a >．【变式训练2-1】、（2022·四川省眉山第一中学高一阶段练习）（1）求值：()1233127863125-⎛⎫⨯++-+⎪⎝⎭（2） 已知 1a a -+= 求44a a -+的值．二、对数运算 1、对数的概念如果a x ＝N (a >0，且a ≠1)，那么x 叫做以a 为底N 的对数，记作x ＝log a N ，其中a 叫做对数的底数，N 叫做真数.2、对数的性质、换底公式与运算性质(1)对数的性质：①a log a N ＝N ；②log a a b ＝b (a >0，且a ≠1). (2)对数的运算法则如果a >0且a ≠1，M >0，N >0，那么①、log a (MN )＝log a M ＋log a N ； ②、log a MN ＝log a M －log a N ；③、log a M n ＝n log a M (n ∈R)； ④、log a m M n ＝nmlog a M (m ，n ∈R ，且m ≠0).(3)换底公式：log b N ＝log a Nlog a b(a ，b 均大于零且不等于1).例3、(1)、（2022·陕西·永寿县中学高一阶段练习）237log 7log 8log 3⋅⋅=______.(2)、（2022·广西·南宁二中高一阶段练习）计算：()1205122log 54⎛⎫--+= ⎪⎝⎭___________.(3)、（2022·陕西渭南·高一期末）已知0a >，且1a ≠，则下列各式恒成立的是（ ） A ．()2log 2log a a x x = B ．2log 2log a a x x =C ．log log log a a a x y x y ⋅=⋅D ．()log log log a a a x y x y +=+【变式训练3-1】、（2022·江西·南昌市第一中学高一阶段练习）)21lg12log 421221(lg 5)lg 2lg 504⎛⎫-+++⋅=⎪⎝⎭______.【变式训练3-2】、（2022·福建·莆田一中高一阶段练习）已知非零实数,,a b c 满足3624a b c ==，则,,a b c 之间的关系是（ ） A ．111b a c=+ B ．312b a c =+ C ．123b a c =+D ．321b a c=+【变式训练3-3】、（2022·江苏徐州·高三学业考试）化简15932log 3-+的值为（ ）A ．0B ．1C ．52D ．32【变式训练3-4】、（2022·河北·21032128log 16(πe)25-+-++=__________.三、混合运算例4、（2022·浙江·高一期中）（1）01430.75337(0.064)(2)168---⎛⎫⎡⎤--+-+ ⎪⎣⎦⎝⎭．（2）3121log 24lg 539--⎛⎫- ⎪⎝⎭．【变式训练4-1】、（2021·陕西省米脂中学高一期中）计算： (1)33lg1000log 42log 14+-；(2)()0.51.500.5162536 1.5494-⎛⎫⎛⎫---- ⎪⎪⎝⎭⎝⎭【变式训练4-2】、（2022·湖北·武汉市第六中学高一阶段练习）计算下列各式的值：(1)1132(0.027)2-+ (2)22ln 2225lg 5lg 2lg 2lg 25log 5log 8e ++⋅+⋅+指、对与幂基本运算参考答案【重难点知识点网络】：【重难点题型突破】： 一、指数运算 1、 根式与分数指数幂(1)、性质：(na )n＝a (a 使na 有意义)；当n 为奇数时，na n＝a ，当n 为偶数时，na n＝|a |＝⎩⎪⎨⎪⎧a ，a ≥0，－a ，a <0.(2)、规定：正数的正分数指数幂的意义是a mn ＝na m (a >0，m ，n ∈N *，且n >1)；正数的负分数指数幂的意义是a －mn ＝1n a m(a >0，m ，n ∈N *，且n >1)；0的正分数指数幂等于0；0的负分数指数幂没有意义.(3)、有理指数幂的运算性质：a r a s ＝a r +s ；(a r )s ＝a rs ；(ab )r ＝a r b r ，其中a >0，b >0，r ，s ∈Q. 例1、(1)、（2022·山东枣庄·高一期中）下列根式与分数指数幂的互化，正确的是（ ）A ．21()x =- B 12y =C ．310)xx -=≠ D ．1432](0)x x =>(2)、（2022·湖南·长沙市同升湖高级中学有限公司高一期中））A ．2B ．532 C ．562D ．762(3)、（2022·黑龙江省饶河县高级中学高一阶段练习）已知16a a -+=，则1122a a --的值为（ ） A ．2 B ．－2 C ．±D ．±2【变式训练1-1】、（2022·湖北·恩施市第一中学高一阶段练习） ） A ．25a - B ．56a -C ．56()a -D ．56()a --【变式训练1-2】、（2022·上海·高一专题练习）已知11224x x -+=，则1x x -+=_______. 【答案】14【变式训练1-3】、（2022·上海市松江二中高一期中）0)a >化成有理数指数幂的形式为______.例3．（2022·江苏·常州市正行中学高一阶段练习）（1）计算：()1020.52312220.0154--⎛⎫⎛⎫+⨯- ⎪ ⎪⎝⎭⎝⎭；（20)a >．【变式训练3-1】、（2022·四川省眉山第一中学高一阶段练习）（1）求值：()12303127863125-⎛⎫⨯++-+ ⎪⎝⎭（2） 已知 1a a -+= 求44a a -+的值．二、对数运算 1、对数的概念如果a x ＝N (a >0，且a ≠1)，那么x 叫做以a 为底N 的对数，记作x ＝log a N ，其中a 叫做对数的底数，N 叫做真数.2、对数的性质、换底公式与运算性质(1)对数的性质：①a log a N ＝N ；②log a a b ＝b (a >0，且a ≠1). (2)对数的运算法则如果a >0且a ≠1，M >0，N >0，那么①、log a (MN )＝log a M ＋log a N ； ②、log a MN ＝log a M －log a N ；③、log a M n ＝n log a M (n ∈R)； ④、log a m M n ＝nmlog a M (m ，n ∈R ，且m ≠0).(3)换底公式：log b N ＝log a Nlog a b(a ，b 均大于零且不等于1).例3、(1)、（2022·陕西·永寿县中学高一阶段练习）237log 7log 8log 3⋅⋅=______.(2)、（2022·广西·南宁二中高一阶段练习）计算：()125122log 54⎛⎫--+= ⎪⎝⎭___________.【答案】32##1.5(3)、（2022·陕西渭南·高一期末）已知0a >，且1a ≠，则下列各式恒成立的是（ ） A ．()2log 2log a a x x = B ．2log 2log a a x x =C ．log log log a a a x y x y ⋅=⋅D ．()log log log a a a x y x y +=+【变式训练3-1】、（2022·江西·南昌市第一中学高一阶段练习）)21lg12log 421221(lg 5)lg 2lg 504⎛⎫-+++⋅=⎪⎝⎭______. 【答案】92##4.5【变式训练3-2】、（2022·福建·莆田一中高一阶段练习）已知非零实数,,a b c 满足3624a b c ==，则,,a b c 之间的关系是（ ） A ．111b a c=+ B ．312b a c =+ C ．123b a c =+D ．321b a c=+【变式训练3-3】、（2022·江苏徐州·高三学业考试）化简15932log 3-+的值为（ ）A ．0B ．1C ．52D ．32【变式训练3-4】、（2022·河北·21032128log 16(πe)25-+-++=__________.【答案】15-##0.2-2132128log 16πe25252311241555故答案为：15-三、混合运算例4、（2022·浙江·高一期中）（1）01430.75337(0.064)(2)168---⎛⎫⎡⎤--+-+ ⎪⎣⎦⎝⎭． （2）3121log 24lg 539--⎛⎫- ⎪⎝⎭．【变式训练4-1】、（2021·陕西省米脂中学高一期中）计算： (1)33lg1000log 42log 14+-；(2)()0.51.500.5162536 1.5494-⎛⎫⎛⎫---- ⎪⎪⎝⎭⎝⎭【变式训练4-2】、（2022·湖北·武汉市第六中学高一阶段练习）计算下列各式的值： (1)1132(0.027)2-+ (2)22ln 2225lg 5lg 2lg 2lg 25log 5log8e ++⋅+⋅+。

根式和分数指数幂的互化及其化简运算专题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 下列各式中正确的一个是（ ） A.(n m)7=n 7m 17 B.√(−3)412=√−33C.√x 3+y 34=(x +y )34 D.√354=3542. 设a >0，将2√a⋅√a 2表示成分数指数幂，其结果是（ ）A.a 12B.a 56C.a 76D.a 323. 当 √2−x 有意义时，化简 √x 2−4x +4−√x 2−6x +9的结果是（ ） A.2x −5 B.−2x −1 C.−1 D.5−2x4. 化简(√a −1)2+√(1−a)2+√(1−a)33的结果是（ ） A.1−a B.2(1−a) C.a −1 D.2(a −1)5. 化简√(x +3)2−√(x −3)33得（ ） A.6 B.2x C.6或−2x D.6或2x 或−2x6. 化简(√√a 963)4⋅(√√a 936)4的结果为（ ） A.a 16 B.a 8 C.a 4 D.a 27. 若x <13，则√9x 2−6x +1等于（ ） A.3x −1 B.1−3xC.(1−3x)2D.非以上答案8. 若n <m <0，则√m 2+2mn +n 2−√m 2−2mn +n 2等于（ ） A.2m B.2n C.−2m D.−2n9. √m ⋅√m 3⋅√m 4⋅=( )A.1B.m 12C.m 13D.m10. 下列各式成立的是（ ） A.√m 2+n 23=(m +n)23 B.(ba)2=a 12b 12C.√(−3)26=(−3)13 D.√√43=21311. 已知正数a ，b 满足√9a×√27b=3，则ab 的最小值为( ) A.6 B.12 C.18 D.2412. 已知a >0，则√a 13√a 12√a 化为( )A.a 712 B.a 512C.a 56D.a 1313. (614)−12=( )A.32B.23C.25D.5214. 若2<a <3，化简√(2−a)2+√(3−a)44的结果是( ) A.5−2a B.2a −5 C.1 D.−115. 已知 a >0 √a 23=( )A.a 12B.a 32C.a 23D.a 1316. 设a >0，将2√a⋅√a 2表示成分数指数幂，其结果是( )A.a 12B.a 56C.a 76D.a 3217. 化简√√ab 23⋅a 3b 2√b 3⋅(a 16b 12)4（a ，b 为正数）的结果是（ ）A.baB.abC.abD.a 2b18. 当x ∈(−∞, 2)时，√(x −2)2+√(x −1)33的值为（ ） A.2x −3 B.1 C.−1 D.−2x +319. 已知x 12+x −12=5，则 x 2+1x的值为（ ）A.5B.23C.25D.2720.(√a⋅√a 35)9(√a 45)3⋅(√a 2⋅√a 5)43(√a 2⋅√a 3)2的值为（ ）A.1B.a 2C.a 3D.以上答案均不正确21. 已知x +x −1=3，则x 32+x −32值为( ) A.±4√5 B.2√5C.4√5D.−4√522. 设a =√(−8)33，b =√(−10)2，则a +b =( ) A.−18 B.18 C.−2 D.223. 已知，，则________．24. 已知 x +x −1=3,则x 2+x −2=________； x 12+x −12=________.25. 已知x +x −1=3，则x 2+x −2=________；x −x −1=________.26. 计算(√23×√3)6+√2√2)43−4×(1649)−12−√24×80.25−(−2013)0=________．27. 已知x +x −1=3，则x 32+x −32值为________．28. 化简√a 72⋅√a −33÷√√a −83⋅√a 153÷√√a −3⋅√a −13=________．29. 已知x +y =12，xy =9，且x <y ，则x 12−y 12x 12+y 12=________．30. 先化简，再求值：，其中.31. 计算(1)√8+√32−√24(2)√12÷√27×√1832. 求下列各式的值： （1）0.001−13−(78)0+1634+(√2⋅√33)6．（2）设 x 12+x −12=3，求x +x −1 的值．33. 已知a <b <0，n >1，n ∈N ∗，化简 √(a −b)n n+√(a +b)n n．34. （1）计算4x 14(−3x 14y −13)÷[−6(x −12y −23)]； 34. （2）√m ⋅√m 3⋅√m 4⋅．35. 化简下列各式（1）√11+6√2+√11−6√2（2）√a 2b 2√ab3(a 14b 12)a−13b13(a >0b >0)36. 解答.(1)求值：√(−27)23+√(2−π)2+√(4−π)44；(2)计算：2x −13(12x 13+x −23)x ；(3)计算：(x 12+2y 14)(x 12−2y 14)÷y −12.37. 化简求值： (1)√254+(√π)0−2−1；(2)(2a 23b 12)(−6a 12b 13)÷(−3a 16b 56). 38. 设x =√3−2，y =√3+2，求代数式x 2+xy+y 2x+y的值．39.(1)求值： (√23×√3)6+(−2020)0−4×(1649)−12+√(3−π)44；(2)已知√a −√a=4，求值：a 12+a −12.40. 化简或求值. b √a 3⋅√ab 3a √b 2√ab3>0,b >0);(2)(214)12+0.1−2−(278)13+π0.参考答案与试题解析根式和分数指数幂的互化及其化简运算专题含答案一、 选择题 （本题共计 22 小题 ，每题 3 分 ，共计66分 ） 1.【答案】 D【考点】根式与分数指数幂的互化及其化简运算 【解析】正确计算各选项，得出答案. 【解答】解：A ，(n m)7=n 7m −7，故A 错误；B ，√(−3)412=√3412=3412=313=√33，故B 错误； C ，√x 3+y 34=(x 3+y 3)14，故C 错误；D ，√354=354，故D 正确.故选D . 2. 【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】由根式与分数指数幂的互化规则所给的根式化简即可将其表示成分数指数幂，求得其结果选出正确选项． 【解答】 解：由题意2√a⋅√a 2=2√a⋅a 23=a 2a 56=a 76.故选C ． 3.【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】解：当 √2−x 有意义时，x ≤2．√x 2−4x +4−√x 2−6x +9=|x −2|−|x −3|=2−x +x −3=−1． 故选C ． 4.【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】解：∵ √a −1 有意义， ∴ a −1≥0，即a ≥1．∴ (√a −1)2+√(1−a)2+√(1−a)33=(a −1)+|1−a|+(1−a)=(a −1)+(a −1)+(1−a)=a −1． 故选C ． 5.【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】化简√(x +3)2−√(x −3)33=|x +3|−(x −3)={6,x ≥−3−2x,x <−3．【解答】解：√(x +3)2−√(x −3)33=|x +3|−(x −3)={6,x ≥−3−2x,x <−3，故选C ． 6. 【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】由根式和分数指数幂的关系，将式子化为分数指数幂形式，再由指数的运算法则求解即可． 【解答】解：(√√a 963)4⋅(√√a 936)4=a 9×16×13×4a 9×13×16×4=a 4 故选C 7.【答案】 B【考点】根式与分数指数幂的互化及其化简运算 【解析】利用|a|={a,a ≥0−a,a <0及其乘法公式即可得出．【解答】解：∵ x <13，∴ 1−3x >0．则√9x 2−6x +1=√(1−3x)2=1−3x ． 故选：B ． 8.【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】利用乘法公式与根式的运算性质即可得出． 【解答】解：原式=|m +n|−|m −n|， ∵ n <m <0，∴ m +n <0，m −n >0，∴ 原式=−(m +n)−(m −n)=−2m ． 故选：C ． 9.【答案】 A【考点】根式与分数指数幂的互化及其化简运算 【解析】将根式化为分数指数幂的形式，从而计算． 【解答】解：√m ⋅√m 3⋅√m 4⋅=m 12⋅m 13⋅m 14⋅m−56⋅m −14=m (12+13+14−56−14) =m 0=1， 故选A ． 10.【答案】 D【考点】根式与分数指数幂的互化及其化简运算 【解析】利用指数幂的运算法则即可得出． 【解答】解：A ．∵ (m +n)23=√(m +n)23，因此不正确； B.(ba )2=b 2⋅a −2，因此不正确； C ．∵√(−3)26=√326=313，因此不正确；D.√√43=223×12=213，正确．11.【答案】 D【考点】基本不等式及其应用根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】解：√9a×√27b=32a +3b=3，即2a +3b =1，∴ ab =3a +2b ≥2√6ab ，解得ab ≥24，当且仅当3a =2b ，即a =4，b =6时，等号成立. 故选D . 12.【答案】 B【考点】根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】解：√a 13√a 12√a=√a 13√a 12⋅a 12 =√a 13⋅a 12=a 12×56=a 512. 故选B . 13. 【答案】 C【考点】根式与分数指数幂的互化及其化简运算 有理数指数幂的化简求值 【解析】【解答】 解：原式=(254)−12=√425=25.故选C . 14.【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】由根式的意义知√x n n=|x|，n 为偶数时，利用此式进行化简即可． 【解答】解：√(2−a)2+√(3−a)44=|2−a|+|3−a|， 因为2<a <3，所以上式=a −2+3−a =1. 故选C. 15. 【答案】 D【考点】根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】 √a 23=a a 23=1a 23−1=a 13.故选D . 16.【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】化根式为分数指数幂，然后利用有理指数幂的运算化简求值． 【解答】 解：2√a⋅√a 2=a 2√a ⋅a 23=a 2√a 1+23=2√a 53=a 2a 56=a 76． 故选C ． 17. 【答案】 C【考点】根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】 解：原式=[(ab 2)13⋅a 3⋅b 2]12b 13⋅a 23⋅b 2=a 16+32−23b 13+1−13−2=ab．故选C ． 18. 【答案】 B【考点】根式与分数指数幂的互化及其化简运算 【解析】根据根式与分数指数幂的运算法则进行化简即可． 【解答】解：∵ x ∈(−∞, 2)时，x −2<0；∴ √(x −2)2+√(x −1)33=|x −2|+(x −1) =−(x −2)+(x −1) =1．故选：B ． 19.【答案】 B【考点】根式与分数指数幂的互化及其化简运算 【解析】根据指数幂的运算法则进行求值即可． 【解答】 解：∵ x 12+x−12=5，∴ 平方得x +2+x −1=25， 即x +x −1=23，∵x2+1x =x+1x=x+x−1，∴x2+1x=23，故选：B．20.【答案】D【考点】根式与分数指数幂的互化及其化简运算【解析】根据根式与分数指数幂的互化进行化简运算即可．【解答】解：原式=a 45×3˙⋅(a2⋅a12)23˙=a125a125⋅a2215a53=a−15，即原式的值为a−15．故选D．21.【答案】B【考点】根式与分数指数幂的互化及其化简运算【解析】由x+x−1=3，得x12+x−12=√5．所以x32+x−32=(x12+x−12)(x+x−1−1)=2√5．【解答】解：∵x+x−1=3，∴x12+x−12=√(x12+x−12)2=√x+x−1+2=√5．∴x32+x−32=(x12+x−12)(x+x−1−1)=2√5．故选B．22.【答案】D【考点】根式与分数指数幂的互化及其化简运算【解析】直接利用有理指数幂的运算性质化简求值．【解答】解：a=√(−8)33=−8，b=√(−10)2=10，则a+b=−8+10=2．故选：D．二、填空题（本题共计 7 小题，每题 3 分，共计21分）23.【答案】23【考点】顺序结构的应用根式与分数指数幂的互化及其化简运算指数式、对数式的综合比较【解析】」利用指数及指数幂的运算律求解．【解答】10∘=210−=3，10−r=10−10∘=23故答案为：2324.【答案】7,√5【考点】有理数指数幂的化简求值根式与分数指数幂的互化及其化简运算分数指数幂【解析】此题暂无解析【解答】解：因为x+x−1=3，所以(x+x−1)2=9，即x2+x−2+2=9，所以x2+x−2=7；∵(x12+x−12)2=x+2+x−1=5，∴x12+x−12=√5.故答案为：7；√5.25.【答案】7,±√5【考点】有理数指数幂根式与分数指数幂的互化及其化简运算【解析】（1）把已知条件平方，再化简即可得解【解答】解：∵(x+x−1)2=x2+x−2+2=9，∴x2+x−2=9−2=7，∴x2+x−2=7，(x −x −1)2=x 2+x −2−2=7−2=5， ∴ x −x −1=±√5. 故答案为：7；±√5. 26.【答案】 100【考点】根式与分数指数幂的互化及其化简运算 有理数指数幂【解析】利用分数指数幂的运算性质即可得出． 【解答】解：原式=22×33+(234)43−4×(47)2×(−12)−214+34−1=108+2−7−2−1 =100．故答案为：100． 27. 【答案】2√5【考点】根式与分数指数幂的互化及其化简运算 【解析】利用完全平方公式和立方差公式即可得出． 【解答】解：∵ (x 12+x −12)2=x +x −1+2=3+2=5， 又∵ x 12+x −12>0，∴ x 12+x −12=√5． ∴ x 32+x−32=(x 12+x −12)(x +x −1−1)=√5(3−1)=2√5．故答案为：2√5． 28. 【答案】a 16【考点】根式与分数指数幂的互化及其化简运算 【解析】本题先将根式化成指数幂的形式，再利用负指数将除转化为乘，然后利用指数运算的法则计算，得到本题的解． 【解答】解：原式=√a 72⋅a −323÷√a −83⋅a 153÷√a −32⋅a −123=√a 23÷√a 73÷√a −23=a 23÷a 76÷a−23=a 16．故答案为：a 1 6．29.【答案】−√3 3【考点】根式与分数指数幂的互化及其化简运算【解析】由题设形式与条件的形式知，需要利用完全平方差公式与完全平方和公式构造出题设中的分子与分母的形式，求值【解答】解：由题设0<x<y∵xy=9，∴√xy=3∴x+y−2√xy=(x12−y12)2=12−6=6x+y+2√xy=(x 12+y12)2=12+6=18∴x12−y12=−√6，x12+y12=3√2∴x 12−y12x 12+y12=√63√2=−√33故答案为：−√33三、解答题（本题共计 11 小题，每题 10 分，共计110分）30.【答案】、x−13、Ex+2′2【考点】运用诱导公式化简求值根式与分数指数幂的互化及其化简运算有理数指数幂【解析】先将除法变为乘法，再约分，再同分化简．然后再将x=√2−2代入求解．【解答】原式=x+2x ×x2(x+2)2−x−2(x+2)(x−2)=xx+2−1x+2=x−1x+2再将x=√2−2代入得：√2−2−1√2−2+2=√2√2=1−3√2231.【答案】【考点】有理数指数幂的化简求值根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】 此题暂无解答 32. 【答案】解：（1）原式 =(0.1)3×(−13)−1+24×34+(212)6⋅(313)6=10−1+8+8×9=89．（2）∵ x 12+x −12=3，∴ x +x−1=(x 12+x −12)2−2=32−2=7．【考点】根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】解：（1）原式 =(0.1)3×(−13)−1+24×34+(212)6⋅(313)6=10−1+8+8×9=89．（2）∵ x 12+x −12=3， ∴ x +x −1=(x 12+x −12)2−2=32−2=7．33.【答案】解：∵ a <b <0，∴ a −b <0，a +b <0． 当n 是奇数时，原式 =(a −b)+(a +b)=2a ；当n 是偶数时，原式= |a −b|+|a +b|=(b −a)+(−a −b)=−2a ． ∴ √(a −b)n n+√(a +b)n n={2a,n 为奇数，−2a,n 为偶数.【考点】根式与分数指数幂的互化及其化简运算 【解析】 此题暂无解析 【解答】解：∵ a <b <0，∴ a −b <0，a +b <0． 当n 是奇数时，原式 =(a −b)+(a +b)=2a ；当n 是偶数时，原式= |a −b|+|a +b|=(b −a)+(−a −b)=−2a ． ∴ √(a −b)n n+√(a +b)n n={2a,n 为奇数，−2a,n 为偶数.34.【答案】解：（1）4x 14(−3x 14y −13)÷[−6(x −12y −23)] =4×(−3)÷(−6)x 14+14−(−12)y −13−(−23)=2xy 13； （2）√m ⋅√m 3⋅√m 4⋅=m 12+13+14m 56+14=m 1312m 1312=1．【考点】根式与分数指数幂的互化及其化简运算 【解析】（1）先把系数运算，再利用有理指数幂的运算性质化简得答案； （2）化根式为分数指数幂，再由有理指数幂的运算性质化简得答案． 【解答】解：（1）4x 14(−3x 14y −13)÷[−6(x −12y −23)] =4×(−3)÷(−6)x14+14−(−12)y−13−(−23)=2xy 13； （2）√m ⋅√m 3⋅√m 4⋅=m 12+13+14m 56+14=m 1312m 1312=1．35. 【答案】解：（1）原式=√9+2√18+2+√9−2√18+2 =√9+√2+√9−√2 =6． （2）原式=(a2+13b 2+13)12a 14−13b 12+13=a 76+112b 76−56=a 53b 13．【考点】根式与分数指数幂的互化及其化简运算 【解析】 （1）（2）利用指数幂的运算法则、乘法公式即可得出． 【解答】解：（1）原式=√9+2√18+2+√9−2√18+2 =√9+√2+√9−√2 =6． （2）原式=(a2+13b 2+13)12a 14−13b 12+13=a76+112b76−56=a 53b 13．36. 【答案】解：(1)√(−27)23+√(2−π)2+√(4−π)44=32+π−2+4−π=9−2+4=11.(2)2x −13(12x 13+x −23)x=(1+2x −1)x =x +2.(3)(x 12+2y 14)(x 12−2y 14)÷y −12=(x −4y 12)y 12=x √y −4y.【考点】根式与分数指数幂的互化及其化简运算 分数指数幂 【解析】解：（1）√(−27)23+√(2−π)2+√(4−π)24=32+π−2+4−π=9−2+4=11（2)2x −13(12x 13+x −23)x =(1+2x −1)x =x +2.（3）(x 12+2y 14)(x 12−2y 14)÷y −12=(x −4y 12)y 12=x √y −4y. 【解答】解：(1)√(−27)23+√(2−π)2+√(4−π)44=32+π−2+4−π=9−2+4=11.(2)2x −13(12x 13+x −23)x=(1+2x −1)x =x +2. (3)(x 12+2y 14)(x 12−2y 14)÷y −12 =(x −4y 12)y 12=x √y −4y.37. 【答案】解：(1)原式=52+1−12=3．(2)原式=[2×(−6)÷(−3)]a 23+12−16 b 12+13−56 =4ab 0 =4a ．【考点】有理数指数幂的化简求值根式与分数指数幂的互化及其化简运算 【解析】 无 无 【解答】解：(1)原式=52+1−12=3． (2)原式=[2×(−6)÷(−3)]a 23+12−16 b12+13−56=4ab 0 =4a ．38. 【答案】 解：∵ x =√3−2=−√3−2，y =√3+2=2−√3，∴ x +y =−2√3，xy =−1， ∴x 2+xy+y 2x+y=(x+y)2−xyx+y=√3)2−2√3=−13√36． 【考点】根式与分数指数幂的互化及其化简运算 【解析】首先化简x ，y ，再化简原式，最后代入计算即可． 【解答】 解：∵ x =√3−2=−√3−2，y =√3+2=2−√3，∴ x +y =−2√3，xy =−1， ∴ x 2+xy+y 2x+y=(x+y)2−xyx+y=√3)2−2√3=−13√36． 39. 【答案】解：(1) 原式=(213×312)6+1−4×(74)(−2)×(−12)+|3−π|=22×33+1−4×74+π−3=99+π. (2)∵ √a −√a=4，∴ a 12−a −12=4， ∴ (a 12−a −12)2=16， ∴ a +a −1=18，∴ (a 12+a −12)2=a +a −1+2=20. ∵ a 12+a −12>0， ∴ a 12+a−12=2√5.【考点】有理数指数幂的化简求值根式与分数指数幂的互化及其化简运算 【解析】(1)将根式转化为分数指数幂进行求解即可； (2)将已知条件两边平方，得到a +a −1=18，再代入(a 12+a −12)2=a +a −1+2=20，即可求解.【解答】解：(1) 原式=(213×312)6+1−4×(74)(−2)×(−12)+|3−π|=22×33+1−4×74+π−3=99+π. (2)∵ √a −√a=4，∴ a 12−a −12=4， ∴ (a 12−a −12)2=16， ∴ a +a −1=18，∴ (a 12+a −12)2=a +a −1+2=20. ∵ a 12+a −12>0， ∴ a 12+a −12=2√5. 40. 【答案】 解：(1)原式=b(a 3(ab)13)12a(b 2(ab)12)13=b×a 32a×b 23=a 12b 13； (2)原式 =(94)12+(110)−2−[(32)3]13+1=32+100−32+1=101.【考点】有理数指数幂的化简求值根式与分数指数幂的互化及其化简运算【解析】（1）利用根式与分数指数幂的运算性质化简运算即可；（2）根式与分数指数幂的运算性质先进行分式指数幂的运算，再化简即可． 【解答】 解：(1)原式=b(a 3(ab)13)12a(b 2(ab)12)13=b×a 32a×b 23=a 12b 13； (2)原式 =(94)12+(110)−2−[(32)3]13+1=32+100−32+1=101.。

2.1.1指数与指数幂的运算重难点题型【举一反三系列】【知识点1 根式的意义】1.n次方根2.根式（1）定义：式子n a叫做根式，这里n叫做根指数，a叫做被开方数．（2）性质：(n＞1，且n∈N*)①nn a )(＝a .②nna ＝⎪⎩⎪⎨⎧为偶数为奇数，n a n a ,,【知识点2 分数指数幂及其运算】 1.分数指数幂（1）意义：nma ＝n ma ，nm a-＝nm a1＝nma 1，其中a ＞0，m ，n ∈N *，n ＞1；（2）0的正分数指数幂等于0，0的负分数指数幂没有意义；（3）规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数． 2．有理数指数幂的运算性质（1）s r a a ＝s r a +a (＞0，r ，s ∈Q )； （2）s r a )(＝rs a a (＞0，r ，s ∈Q )； （3）r ab )(＝r r b a a (＞0，r ，s ∈Q )．3．无理数指数幂一般地，无理数指数幂αa (a ＞0，α是无理数)是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．【知识点3 化简求值的方法与技巧】（1）在进行幂和根式的化简时，一般是先将根式化成幂的形式，并化小数指数幂为分数指数幂，并尽可能统一成分数指数幂的形式，再利用分数指数幂的性质进行化简、求值、计算. （2）结果必须化为最简的形式.（3）巧妙公式变形：完全平方公式，立方和、立方差等.【考点1 根式的化简】【例1】（2019秋•信阳期中）式子( ) ABC．D．【变式2-1】（2019秋•中原区校级期中）当0a >(= )A ．B ．C ．-D ．-【变式2-2】（2019秋•32(0)a a a >的结果是( )A B C D【变式2-3】（2019秋•九龙坡区校级期中）把(a -根号外的(1)a -移到根号内等于( )A ．BC ．D 【考点2 根式与分数指数幂互化】【例2】（2019秋•( ) A ．35a -B ．53aC ．35aD ．53a -【变式2-1】下列关系式中，根式与分数指数幂互化正确的是( )A 56aa a -=-B ．24x =C ．332b =D ．52()a b --=【变式2-2】（2019秋•桐庐县期中）下列根式中，分数指数幂的互化，正确的是( )A ．12()(0)x x =-> B 13(0)y y <C ．340)xx ->D ．130)xx -=≠【变式2-3】（2019秋•城关区校级期中）若0a >，则用根式形式表示35a -为和．( ) A532a bB ，1235a bC532a bD 1235b b【考点3 多重根式的化简】【例3】（2019秋•3a a a 的分数指数幂表示为( )A ．32aB ．3aC ．34aD ．都不对【变式3-1】（2019秋•等于( )A ．B ．2 CD ．2【变式3-2】（2019秋•凌源市月考）已知0a >( )A ．712aB ．512aC ．56aD ．13a 【变式3-3】（2019秋•(0)a >为( ) A ．56aB ．16aC ．112a-D ．13a -【考点4 根式与分数指数幂的混合运算】 【例4】（2019秋•巴宜区校级期中） （1）2102329272()(9.6)()()483---+（2）1323422()ab b a ---÷【变式4-1】（2019秋•鸠江区校级期中） （121xy xy-；（21327()8-++．【变式4-2】（2019秋•温江区校级月考）计算： （1）210232983()( 2.5)()()4272----+；（2）10.523321(4()0,0)4(0.1)()ab a b a b ---->>．【变式4-3】（2019秋•石河子校级月考）计算下列各式的值：（10,0)a b >>，（2）210232183(2)(9.6)()()4272----+．【考点5 利用整体代换思想求值】 【例5】（2019秋•凌源市月考）已知11223x x --=．求：（1）1x x -+； （2）1x x --．【变式5-1】（2019秋•沙坪坝区校级期中）若1122x x-+，求12212x x x x --+-+-的值．【变式5-2】（2019秋•越秀区校级月考）已知12x y +=，9xy =且x y <，求11221122x y x y-+的值．【变式5-3】（2018秋•湛江校级月考）已知11223a a -+=，求3322a a-+的值．【考点6 幂的综合应用】【例6】已知333ax by cz ==，且1111x y z++=，求证：11112223333()ax by cz a b c ++=++．【变式6-1】（2019秋•临沂期中）已知33()5x x f x --=，33()5x x g x -+=．（1）求证：()f x 是奇函数，并求()f x 的单调区间；（2）分别计算f （4）5f -（2）g （2）和f （9）5f -（3）g （3）的值，由此概括出涉及函数()f x 和()g x 对所有不等于零的实数x 都成立的一个等式，并加以证明．【变式6-2】（2019秋•双桥区校级期末）设函数4()42xx f x =+，若01a <<，试求：（1）求f （a ）(1)f a +-的值；（2）求1231000()()()()1001100110011001f f f f +++⋯+的值．【变式6-3】设正整数a 、b 、()c a b c 剟和实数x 、y 、z 、ω满足：30x y z a b c ω===，1111x y z ω++=，求a 、b 、c 的值．。