高一【数学(人教A版)】根式与分数指数幂-练习题
- 格式:docx
- 大小:40.28 KB
- 文档页数:1


分数指数幂活动一:复习引入:1.整数指数幂的运算性质:===⋅n n m n m ab a a a )()()(),(),(Z n Z n m Z n m ∈∈∈2.根式的运算性质:①当n 为任意正整数时,(n a )n=. ②当n 为奇数时,n n a = ;当n 为偶数时,n na =|a|=⎩⎨⎧<-≥)0()0(a a a a . 用语言叙述上面三个公式:⑴非负实数a 的n 次方根的n 次幂是它本身.⑵n 为奇数时,实数a 的n 次幂的n 次方根是a 本身;n 为偶数时,实数a 的n 次幂的n 次方根是a 的绝对值.3.引例:当a >0时 ①5102552510)(a a a a===②=312a ③32333232)(a a a ==④=a 上述推导过程主要利用了根式的运算性质,例子③、④、⑤用到了推广的整数指数幂运算性质(2).因此,我们可以得出正分数指数幂的意义.活动二:建构数学:1.正数的正分数指数幂的意义n m n ma a = (a >0,m ,n ∈N *,且n >1) 要注意两点:一是分数指数幂是根式的另一种表示形式;二是根式与分数指数幂可以进行互化. 另外,我们还要对正数的负分数指数幂和0的分数指数幂作如下规定.2.规定: (1)n mn ma a 1=- (a >0,m ,n ∈N *,且n >1);(2)0的正分数指数幂等于0;(3)0的负分数指数幂无意义.规定了分数指数幂的意义以后,指数的概念就从整数推广到有理数指数.当a >0时,整数指数幂的运算性质,对于有理指数幂也同样适用.即对于任意有理数r,s,均有下面的运算性质.3.有理指数幂的运算性质:)())....(3(),())....(2(),().....1(Q n b a ab Q n m a a Q n m a a a n n n mn n m n m n m ∈⋅=∈=∈=⋅+说明:若a >0,P 是一个无理数,则p a 表示一个确定的实数,上述有理指数幂的运算性质,对于无理数指数幂都适用,有关概念和证明在本书从略.活动三:应用数学: 例1求值:4332132)8116(,,,,,,)41(,,,,,100,,,,,,8---. 解:=328 ===---43321)8116()41(100 例2 用分数指数幂的形式表示下列各式:a a a a a a ,,,,,,,,,,,3232••(式中a >0) 解:252122122a a a a a a ==⋅=⋅+ ==⋅a a a a 323例3计算下列各式(式中字母都是正数):.))(2();3()6)(2)(1(88341656131212132n m b a b a b a -÷-aab b ab a b a b a 44)]3()6(2[)3()6)(2)(1(0653121612132656131212132==-÷-⨯=-÷-++++88341))(2(n m 例4计算下列各式: 433225)12525)(2();0()1(÷->a a a a解:活动四:理解数学:(课本练习)1.用根式的形式表示下列各式(a>0):32534351,,,--a aa a . 解:551a a =; ====---32535353431a a a aa 2.用分数指数幂表示下列各式: (1)32x ; (2)43)(b a +(a+b>0) ;(3)32)(n m -;(4)4)(n m -(m>n); (5)56q p ⋅(p>0); (6)m m 3. 解:(1)3232x x =; (2)4343)()(b a b a +=+; (3)3232)()(n m n m -=-; 322)1(a a a •435)12525)(2(÷-【课后提升】1.计算:48373)27102(1.0)972(03225.0+-++--π. 解:原式48373)2764(1.01)925(32221+-++=- 1004837316910035=+-++=. 2.已知:32121=+-a a ,求21212323----a a aa .3.化简)21)(21)(21)(21)(21(214181161321-----+++++=s4.若x >0,y >0且)5(3)(y x y y x x +=+,求y xy x y xy x +-++322值.5.已知:+-∈-=N n x n n ),55(2111,求n x x )1(2++的值.。
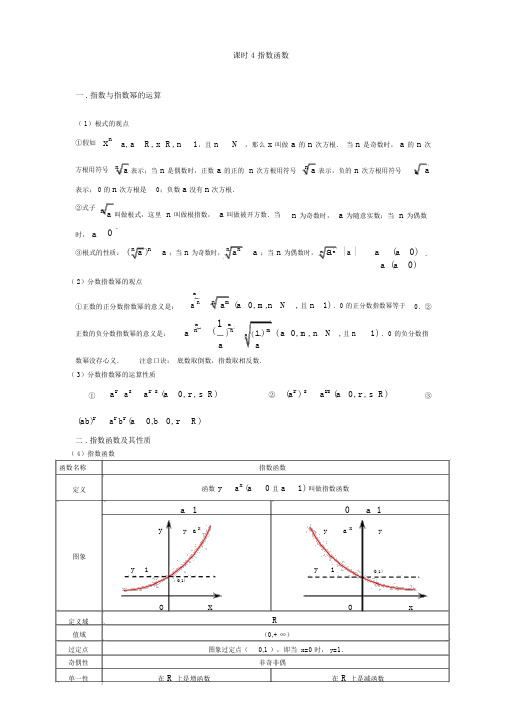
课时 4 指数函数一 . 指数与指数幂的运算( 1)根式的观点①假如xna, a R, x R, n 1,且 nN ,那么 x 叫做 a 的 n 次方根. 当 n 是奇数时, a 的 n 次方根用符号 na 表示;当 n 是偶数时,正数 a 的正的 n 次方根用符号na 表示,负的 n 次方根用符号na表示; 0 的 n 次方根是 0;负数 a 没有 n 次方根.②式子 n a 叫做根式,这里 n 叫做根指数, a 叫做被开方数.当n 为奇数时, a 为随意实数;当 n 为偶数时, a.③根式的性质: (na )n a ;当 n 为奇数时, n a n a ;当 n 为偶数时, n a n | a |a (a 0) .a (a 0)( 2)分数指数幂的观点mna m (a①正数的正分数指数幂的意义是:a n 0, m,n N , 且 n 1) .0 的正分数指数幂等于0.②m(1m1 ) m( a正数的负分数指数幂的意义是:a n)n n (0, m, n N , 且 n1) .0 的负分数指aa数幂没存心义. 注意口诀: 底数取倒数,指数取相反数.( 3)分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质( 4)指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域(0,+ ∞)过定点 图象过定点(0,1 ),即当 x=0 时, y=1.奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y > 1(x > 0), y=1(x=0), 0< y < 1(x < 0)y > 1(x < 0), y=1(x=0), 0< y < 1(x > 0)变化状况a 变化对在第一象限内, a 越大图象越高,越凑近 y 轴; 在第一象限内, a 越小图象越高,越凑近 y 轴; 图象影响在第二象限内,a 越大图象越低,越凑近x 轴.在第二象限内,a 越小图象越低,越凑近x 轴.三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析: A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析: 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= [ f(x) ] nD.f [ (xy) n ] =[ f(x) ] n [ f(y) ] n (n ∈ N * )分析: 易知 A 、 B 、 C 都正确 .对于 D,f [(xy)n] =a (xy)n , 而[ f(x) ] n ·[f(y) ] n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析: a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析: 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析: 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. [ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析: 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ] ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析: 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈[ -1,1]时 ,函数 f(x)=3 x-2 的值域为 _______[ -5,1 ] ___________.3分析: f(x) 在[ -1,1 ]上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析: (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩[ 2,+ ∞]=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈[ -3,2]的最大值和最小值 .解: 设 2-x=t, 由 x ∈[ -3,2 ]得 t ∈[ 1,8 ] , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解: ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. [ 1,2]B.[ 2,3]C.(-∞ ,2]D.[ 2,+∞ )分析: 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈[ 2,+ ∞ ) 上递加 , 故所求的递加区间为[ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. [ -1,+∞ )B. [ -1,63)C.[ 0,+∞ )D.(0,63 ]分析: 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= [ f(x)-1 ]2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈[ 1,9 ].2.1 指数函数练习1.以下各式中建立的一项A . ( n)71n 7 m 7B .12 ( 3)433m3C . 4 x 3y 3( x y) 4D .393321111 1 52.化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D . 9a 2 A . 6aB . aC . 9a3.设指数函数 f ( x)a x ( a 0, a1) ,则以下等式中不正确的选项是f (x) A . f(x+y)=f(x) ·f(y)B . f ( x y )f ( y)C . f (nx)[ f ( x)]n (nQ )D . f ( xy) n [ f ( x)] n ·[f ( y)] n1 4.函数 y (x5) 0 ( x 2)2A . { x | x 5, x 2}B . { x | x 2}C . { x | x 5}D . { x | 2 x 5或 x 5}()()()(n N )( )5.若指数函数 y a x 在 [- 1,1]上的最大值与最小值的差是1,则底数 a 等于 ()A .15 B .1 5 C .15D .5 122 226.当 a0 时,函数 y axb 和 yb ax 的图象只可能是()7.函数 f ( x)2 |x| 的值域是()A . (0,1]B . (0,1)C . (0, )D . R8.函数 f ( x)2 x 1, x 0,知足 f ( x)1的 x 的取值范围1x 2 , x()A . ( 1,1)B . ( 1, )C . { x | x 0或 x2}D . { x | x 1或 x1}9.函数 y(1) x 2x2得单一递加区间是2()A .[ 1,1]B . ( , 1]C .[2,)D .[ 1,2]2exe x210.已知 f ( x)()2 ,则以下正确的选项是A .奇函数,在 R 上为增函数B .偶函数,在 R 上为增函数C .奇函数,在 R 上为减函数D .偶函数,在 R 上为减函数11.已知函数 f (x)的定义域是(1, 2),则函数 f (2 x ) 的定义域是.12.当 a >0 且 a ≠1 时,函数 f (x)=a x -2- 3 必过定点.三、解答题:13.求函数 y1的定义域 .x5 x 1114.若 a >0, b > 0,且 a+b=c ,求证: (1) 当r >1时, a r +b r < c r ; (2) 当r < 1时, a r +b r > c r .a x 1 15.已知函数 f ( x)(a >1) .a x1( 1)判断函数 f (x) 的奇偶性;( 2)证明 f (x)在 (-∞, +∞ )上是增函数 .xa16.函数 f(x) = a (a>0 ,且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2,求 a 的值.参照答案一、 DCDDD AADDA二、 11. (0,1);12. (2,- 2) ;三、 13. 解:要使函数存心义一定:x 1 0x 1x0 x 0x 1∴ 定义域为 : x xR 且 x0, x 1a rrrb r此中a1,0b114. 解:ba,c rcccc.r >1 ,a rb ra b 1,r r r当因此+b< c ;时c c c crrrrr当 r < 1 时, aba b1, 因此 a +b >c .ccc c15. 解 :(1)是奇函数 .(2) 设x <x ,则 f (x 1 )ax11 ax21 。

根式和分数指数幂例1 求使等式(a -3)(a 2-9)=(3-a )a +3成立的实数a 的取值范围. 解(a -3)(a 2-9)=(a -3)2(a +3)=|a -3|a +3, 要使|a -3|a +3=(3-a )a +3成立, 需⎩⎪⎨⎪⎧a -3≤0,a +3≥0,解得a ∈[-3,3]. 跟踪训练1 若a 2-2a +1=a -1,求a 的取值范围.解 ∵a 2-2a +1=|a -1|=a -1,∴a -1≥0,∴a ≥1. 例2 化简:(1)4(3-π)4; (2)(a -b )2(a >b );(3)(a -1)2+(1-a )2+3(1-a )3.解 (1)4(3-π)4=|3-π|=π-3. (2)(a -b )2=|a -b |=a -b .(3)由题意知a -1≥0,即a ≥1.原式=a -1+|1-a |+1-a =a -1+a -1+1-a =a -1. 跟踪训练2 求下列各式的值:(1)7(-2)7; (2)4(3a -3)4(a ≤1); (3)3a 3+4(1-a )4. 解 (1)7(-2)7=-2. (2)4(3a -3)4=|3a -3|=3|a -1|=3-3a .(3)3a 3+4(1-a )4=a +|1-a |=⎩⎪⎨⎪⎧1,a ≤1,2a -1,a >1.例3 设-3<x <3,求x 2-2x +1-x 2+6x +9的值.解 原式=(x -1)2-(x +3)2=|x -1|-|x +3|,∵-3<x <3,∴当-3<x <1时,原式=-(x -1)-(x +3)=-2x -2; 当1≤x <3时,原式=(x -1)-(x +3)=-4.∴原式=⎩⎪⎨⎪⎧-2x -2,-3<x <1,-4,1≤x <3.1.已知x 5=6,则x 等于( )A. 6B.56 C .-56 D .±56 答案 B2.m 是实数,则下列式子中可能没有意义的是( ) A.4m 2 B.3m C.6m D.5-m 答案 C3.(42)4运算的结果是( )A .2B .-2C .±2D .不确定 答案 A4.3-8的值是________. 答案 -25.(a -b )2+5(a -b )5的值是________. 答案 0或2(a -b )解析(a -b )2+5(a -b )5=|a -b |+(a -b )=⎩⎪⎨⎪⎧0,a ≤b ,2(a -b ),a >b .例1 用根式的形式表示下列各式(x >0).25(1);x 53(2).x -解 (1) 25x =5x 2. (2)53x-=13x 5.跟踪训练1 用根式表示2132x y -(x >0,y >0).解221332121xy y x-=⋅=例2 把下列根式化成分数指数幂的形式,其中a >0,b >0.(1)5a 6; (2)13a 2; (3)4b 3a 2; (4)(-a )6.解65.a=23231.aa-==(3)4b3a2132133444242.bb a a aa--⎛⎫===⎪⎝⎭632.a a===跟踪训练2把下列根式化成分数指数幂:(1) 682;(2) a a(a>0);(3)b3·3b2;(4)13x(5x2)2.解1776212(2)2;===313224();a a ====(3)2113333;b b b b=⋅=3591353511.()xx x-======例3计算下列各式(式中字母都是正数):(1)10.5233177(0.027)2;1259-⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭解10.5233177(0.027)21259-⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭=(30.027)2+312527-259=0.09+53-53=0.09.(2)211511336622(2)(6)(3);a b a b a b-÷-解原式=211115326236[2(6)(3)]44.a b ab a+-+-⨯÷--==(3)111222.m mm m--+++解1111122222111122222().m m m mm mm m m m-----+++==+++跟踪训练3(1)化简:130.256178;86-⎛⎫⎛⎫⨯-+⎪ ⎪⎝⎭⎝⎭解 原式=1111131(1)()36623334424481(2)2(2)(3)2223112.-⨯-+⨯+⨯+⨯=+++=(2)化简:213211113625;1546x yx y x y ---⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭解 212111132(1)()332261111362565(4)51546x y x yx y x y -⎛⎫------- ⎪⎝⎭--⎛⎫=⨯-⨯-⨯⨯ ⎪⎛⎫⎛⎫⎝⎭-- ⎪ ⎪⎝⎭⎝⎭110662424.x y y ==(3)已知11225,x x -+=求x 2+1x 的值.解 由11225,x x-+=两边同时平方得x +2+x -1=25,整理,得x +x -1=23,则有x 2+1x=23.例4 已知a >0,b >0,且a b =b a ,b =9a ,求a 的值.解 方法一 ∵a >0,b >0,又a b =b a ,1119()()(9),a b a bbba b a b a a ∴=⇒=⇒=81829993a a a ∴=⇒=⇒=方法二 ∵a b =b a ,b =9a ,∴a 9a =(9a )a ,即(a 9)a =(9a )a ,∴a 9=9a ,a 8=9,a =43.跟踪训练4 已知67x =27,603y =81,求3x -4y 的值.解 由67x=33,3673,x =得由603y=81,46033,y=得433y x-∴=60367=9=32,∴4y -3x =2,故3x -4y=-2. 1.化简238的值为( )A .2B .4C .6D .8 答案 B 2.1225-等于( )A .25 B.125 C .5 D.15答案 D3.下列根式与分数指数幂的互化正确的是( ) A .-x =12()(0)x x ->B.6y 2=13(0)y y <C .340)xx -=>D .130)xx -=≠答案 C4.(36a 9)4=________.答案 a 25.计算122-⨯________.答案 16。


4.1 指数考点1:n 次方根的概念问题1. a 的n 次方根定义:如果x n =a ,那么x 叫做a 的n 次方根,其中n >1,且n ∈N *.2. a 的n 次方根的表示x n=a ∈⎩⎨⎧x =n a ,当n 为奇数且n ∈N *,n >1时,x =±n a ,当n 为偶数且n ∈N *时.【例1】(1)8的立方根是________. (2)已知x 6=2021,则x =________.(3)若4x +3有意义,则实数x 的取值范围为________. 【答案】(1)3 (2)±62 019 (3)[-3,+∞) 【解答】(1)8的立方根是2. (2)因为x 6=2 021,所以x =±62021.(3)要使4x +3有意义,则需要x +3≥0,即x ≥-3. 所以实数x 的取值范围是[-3,+∞). 【方法技巧】n 次方根的个数及符号的确定(1)n 的奇偶性决定了n 次方根的个数; (2)n 为奇数时,a 的正负决定着n 次方根的符号. 【针对训练】1.已知a ∈R ,n ∈N *,给出下列4个式子:∈6(-3)2n ;∈5a 2;∈6(-5)2n +1;∈9-a 2,其中无意义的有( ) A .1个 B .2个 C .3个 D .0个【解析】A ∈中(-3)2n >0,所以6(-3)2n 有意义;∈中根指数为5有意义;∈中(-5)2n+1<0,因此无意义;∈中根指数为9,有意义.选A考点2:利用根式的性质化简求值考点讲解1.根式的性质(n >1,且n ∈N *) ① n a n =⎩⎪⎨⎪⎧a ,n 为奇数,|a |=⎩⎪⎨⎪⎧a ,a ≥0,-a ,a <0,n 为偶数. ②n 0=0.③ 负数没有偶次方根. 【例2】 化简下列各式:(1)5(-2)5+(5(-2))5;(2)6(-2)6+(62)6;(3)4(x +2)4. 【解答】 (1)原式=(-2)+(-2)=-4. (2)原式=|-2|+2=2+2=4.(3)原式=|x +2|=⎩⎪⎨⎪⎧x +2,x ≥-2.-x -2,x <-2.【方法技巧】正确区分n a n 与(na )n(1)(n a )n 已暗含了na 有意义,据n 的奇偶性可知a 的范围; (2)n a n 中的a 可以是全体实数,na n 的值取决于n 的奇偶性. 【针对训练】2.若9a 2-6a +1=3a -1,求a 的取值范围. 【解答】 ∈9a 2-6a +1=(3a -1)2=|3a -1|, 由|3a -1|=3a -1可知3a -1≥0,∈a ≥13.故a 的取值范围为⎣⎡⎭⎫13,+∞.考点3:根式与分数指数幂的互化∈ 正分数指数幂:a mn =na m (a >0,m ,n ∈N *,且n >1); ∈ 负分数指数幂:a -mn =1a m n=1na m (a >0,m ,n ∈N *,且n >1);∈ 0的正分数指数幂等于0,0的负分数指数幂无意义.【例3】 将下列根式化成分数指数幂的形式:(1)a a (a >0);(2)()32521x x;(3)32432--⎪⎪⎭⎫⎝⎛b(b >0). 【解答】 (1)原式===⋅2321a a a 432123a a =⎪⎪⎭⎫⎝⎛(2)原式=53533159359354325211111-==⎪⎪⎭⎫ ⎝⎛==⋅=⎪⎪⎭⎫ ⎝⎛x xx xxx x x .(3)原式=91324132324132b bb ==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-⨯⨯---【方法技巧】根式与分数指数幂互化的规律 (1)根指数分数指数的分母,被开方数(式)的指数分数指数的分子.(2)在具体计算时,通常会把根式转化成分数指数幂的形式,然后利用有理数指数幂的运算性质解题.【针对训练】3.将下列根式与分数指数幂进行互化: (1)a 3·3a 2;(2)a -4b 23ab 2(a >0,b >0).【解答】 (1)a 3·3a 2=a 3·a 23=a 3+23=a 113. (2)a-4b 23ab 2=a-4b 2·(ab 2)13=a-4b 2a13b 23=a -113b 83=a -116b 43.考点4:利用分数指数幂的运算性质化简求解【例4】 化简求值:(1)()0132432131322256416027.0π+-++⎪⎭⎫⎝⎛--(2)()()()c b ab a ba 24132124-----÷-⋅(3)363342b ab a ⨯÷【解答】(1)原式=()()1576413124253.03223434212313=+-⎪⎪⎭⎫ ⎝⎛++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛- (2)原式=()cac b a c b a ba331124-1)2(2)4(3241312-=-=÷---------+---(3)原式=34612361613123342b a b b a a =⎪⎪⎭⎫⎝⎛⨯⎪⎪⎭⎫ ⎝⎛÷【方法技巧】 指数幂运算的常用技巧(1)有括号先算括号里的,无括号先进行指数运算. (2)负指数幂化为正指数幂的倒数.(3)底数是小数,先要化成分数;底数是带分数,要先化成假分数,然后要尽可能用幂的形式表示,便于用指数幂的运算性质.提醒:化简的结果不能同时含有根式和分数指数,也不能既含有分母又含有负指数. 【针对训练】4.(1)计算:212-04122532-⎪⎭⎫⎝⎛⨯+⎪⎭⎫ ⎝⎛-(0.01)0.5;(2)化简:313315383327----⋅÷⋅÷a a a a a a(a >0).【解答】(1)原式=15161016111001944112121=-+=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⨯+(2)原式=661321233153832327a a a a a a aa ==⋅÷⋅÷⋅----考点5:有限制条件的根式的运算【例5】(1)若x <0,则x +|x |+x 2x =________.(2)若-3<x <3,求x 2-2x +1-x 2+6x +9的值. 【解答】(1)-1 [∈x <0,∈|x |=-x ,x 2=|x |=-x , ∈x +|x |+x 2x =x -x -1=-1.](2)x 2-2x +1-x 2+6x +9 =(x -1)2-(x +3)2=|x -1|-|x +3|,当-3<x ≤1时,原式=1-x -(x +3)=-2x -2. 当1<x <3时,原式=x -1-(x +3)=-4.因此,原式=⎩⎪⎨⎪⎧-2x -2,-3<x ≤1,-4,1<x <3.带条件根式的化简(1)有条件根式的化简问题,是指被开方数或被开方的表达式可以通过配方、拆分等方式进行化简.(2)有条件根式的化简经常用到配方的方法.当根指数为偶数时,在利用公式化简时,要考虑被开方数或被开方的表达式的正负.考点6:指数幂运算中的条件求值【例6】 已知42121=+-aa ,求下列各式的值:(1)a +a -1;(2)a 2+a -2. 【解答】 (1)将42121=+-aa 两边平方,得a +a -1+2=16,故a +a -1=14.(2)将a +a -1=14两边平方,得a 2+a -2+2=196,故a 2+a -2=194.【方法技巧】 解决条件求值的思路(1)在利用条件等式求值时,往往先将所求式子进行有目的的变形,或先对条件式加以变形,沟通所求式子与条件等式的联系,以便用整体代入法求值.(2)在利用整体代入的方法求值时,要注意完全平方公式的应用.1.注意n a n 同(na )n 的区别.前者求解时,要分n 为奇数还是偶数,同时要注意实数a 的正负,而后者(n a )n =a 是恒等式,只要(na )n 有意义,其值恒等于a .2.一个数到底有没有n 次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n 为奇数或偶数这两种情况.3.对根式进行运算时,一般先将根式化成分数指数幂,这样可以方便使用同底数幂的运算律.4.解决较复杂的条件求值问题时,“整体思想”是简化求解的“利器”.一、选择题1.下列等式中成立的个数是( ) ∈(na )n=a (n ∈N *且n >1);∈na n=a (n 为大于1的奇数);∈na n=|a |=⎩⎪⎨⎪⎧a ,a ≥0,-a ,a <0(n 为大于零的偶数).A .0个B .1个C .2个D .3个【解答】D 由n 次方根的定义可知∈∈∈均正确. 2.若a -2+(a -4)0有意义,则a 的取值范围是( ) A .[2,+∞) B .[2,4)∈(4,+∞) C .(-∞,2)∈(2,+∞)D .(-∞,4)∈(4,+∞)知识小结考点演练【解答】B 由题意可知⎩⎪⎨⎪⎧a -2≥0,a -4≠0,∈a ≥2且a ≠4.3.化简(x +3)2-3(x -3)3等于( ) A .6 B .2xC .6或-2xD .6或-2x 或2x【解答】C 原式=|x +3|-(x -3)=⎩⎪⎨⎪⎧6,x ≥-3,-2x ,x <-3,故选C.4.下列各式运算错误的是( ) A .(-a 2b )2·(-ab 2)3=-a 7b 8 B .(-a 2b 3)3÷(-ab 2)3=a 3b 3 C .(-a 3)2·(-b 2)3=a 6b 6 D .[-(a 3)2·(-b 2)3]3=a 18b 18【解答】C 对于A ,(-a 2b )2·(-ab 2)3=a 4b 2·(-a 3b 6)=-a 7b 8,故A 正确;对于B ,(-a 2b 3)3÷(-ab 2)3=-a 6b 9÷(-a 3b 6)=a 6-3b 9-6=a 3b 3,故B 正确;对于C ,(-a 3)2·(-b 2)3=a 6·(-b 6)=-a 6b 6,故C 错误;对于D ,易知正确,故选C.5.已知xy ≠0且4x 2y 2=-2xy ,则有( ) A .xy <0 B .xy >0 C .x >0,y >0 D .x <0,y >0【解答】A4x 2y 2=-2xy ≥0,又xy ≠0,∈xy <0.6.若n <m <0,则m 2+2mn +n 2-m 2-2mn +n 2等于( ) A .2m B .2n C .-2mD .-2n【解答】C 原式=(m +n )2-(m -n )2=|m +n |-|m -n |,∈n <m <0,∈m +n <0,m -n >0,∈原式=-(m +n )-(m -n )=-2m .7.若(1-2x )-34有意义,则x 的取值范围是( ) A .(-∞,+∞) B.⎝⎛⎭⎫-∞,12∈⎝⎛⎭⎫12,+∞ C.⎝⎛⎭⎫12,+∞ D.⎝⎛⎭⎫-∞,12 【解答】D ∈(1-2x ) -34=14(1-2x )3,∈1-2x >0,得x <12.8.已知ab =-5,则a -b a +b -ab 的值是( ) A .2 5 B .0 C .-2 5D .±25【解答】B 由题意知ab <0,a -ba +b -a b =a -ab a 2+b -ab b 2=a 5a 2+b 5b 2=a5|a |+b 5|b |=0,故选B. 二、填空题10.若81的平方根为a ,-8的立方根为b ,则a +b =________. 【答案】-11或7【解析】因为81的平方根为±9,所以a =±9. 又因为-8的立方根为b ,所以b =-2,所以a +b =-11或a +b =7.11.若x -1+4x +y =0,则x 2 019+y 2 020=________. 【答案】0【解析】∈x -1≥0,4x +y ≥0,且x -1+4x +y =0,∈⎩⎪⎨⎪⎧x -1=0,x +y =0,即⎩⎪⎨⎪⎧x =1,y =-1. ∈x 2 019+y 2 020=-1+1=0.12.已知4(a -1)4+1=a ,化简(a -1)2+(1-a )2+3(1-a )3=________. 【答案】a -1【解析】由已知4(a -1)4+1=a , 即|a -1|=a -1,即a ≥1.所以原式=(a -1)+(a -1)+(1-a )=a -1. 13.已知3a =2,3b =15,则32a -b =________.【答案】20【解析】32a -b =32a 3b =(3a )23b =2215=20. 14.已知2121--a a =5,则2121--aa =________.【答案】3【解析】因为22121⎪⎪⎭⎫ ⎝⎛--a a =a +a -1+2=22121⎪⎪⎭⎫ ⎝⎛--a a +4=5+4=9.又因为3,021212121=+>+--aa a a 所以14.设2x =8y +1,9y =3x -9,则x +y =________. 【答案】27【解析】由2x =8y +1,得2x =23y +3, 所以x =3y +3.∈ 由9y =3x -9,得32y =3x -9,所以2y =x -9. ∈由∈∈联立方程组,解得x =21,y =6, 所以x +y =27.1.求下列各式的值:(1)432981⨯(2)63125.132⨯⨯(3)5.1213241-916449270001.0--⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛-+【解答】(1)原式=667413244121344333333==⎪⎪⎭⎫ ⎝⎛=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⨯+ (2)原式=()632322323326131213131-16123121=⨯=⨯=⨯⨯⎪⎭⎫ ⎝⎛⨯⨯+++(3)原式=()()()73142778910318731.0318731.03121-5.1221232341-4=+-+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛-+---⨯⎪⎭⎫ ⎝⎛-⨯2.化简:(1)n(x -π)n (x <π,n ∈N *);(2)4a 2-4a +1⎝⎛⎭⎫a ≤12. 【解答】(1)∈x <π,∈x -π<0, 当n 为偶数时,nx -πn=|x -π|=π-x ;巩固提升当n 为奇数时,nx -πn=x -π.综上,nx -πn =⎩⎪⎨⎪⎧π-x ,n 为偶数,n ∈N *,x -π,n 为奇数,n ∈N *. (2)∈a ≤12,∈1-2a ≥0,∈4a 2-4a +1=2a -12=|2a -1|=1-2a .3.设-2<x <2,求x 2-2x +1-x 2+4x +4的值. 【解答】原式=x -12-x +22=|x -1|-|x +2|,∈-2<x <2, ∈当-2<x <1时,原式=-(x -1)-(x +2)=-2x -1; 当1≤x <2时,原式=x -1-(x +2)=-3.∈原式=⎩⎪⎨⎪⎧-2x -1,-2<x <1,-3,1≤x <2.4.已知x +y =12,xy =9,且x >y ,求x 12-y 12x 12+y 12的值.【解答】∈x +y =12,xy =9,∈(x -y )2=(x +y )2-4xy =108. ∈x >y ,∈x -y =63,∈x 12-y 12x 12+y 12=(x 12-y 12)2(x 12+y 12)(x 12-y 12)=x +y -2x 12y 12x -y =x +y -2(xy )12x -y =12-2×91263=663=33.。




高一数学幂函数试题答案及解析1. (1)化简;(2)已知且,求的值.【答案】(1)1; (2)【解析】(1)注意根式与分数指数幂的关系:,将所求式子全用分数指数幂来表示,再利用幂的运算法则:可化简已知式子;(2)注意到,将已知代入即可求得所求式子的平方值,再注意到,所以>0,从而就可得到所求式子的值.试题解析:原式.(2).又因为,所以故知:.【考点】根式与分数指数幂的运算.2.若上述函数是幂函数的个数是()A.个B.个C.个D.个【答案】C【解析】形如的函数,是幂函数。
所以幂函数有,共两个,故选C。
【考点】本题主要考查幂函数的概念。
点评:简单题,形如的函数,是幂函数。
3.当时,幂函数为减函数,则实数( )A.m=2B.m=-1C.m=2或m=-1D.【答案】A【解析】因为,当时,幂函数为减函数,所以或,解得,m=2,故选B。
【考点】本题主要考查幂函数的概念及其性质。
点评:简单题,注意形如为常数)的函数是幂函数。
4.已知幂函数在增函数,则的取值范围 .【答案】(0,10)【解析】根据已知表达式可知,幂函数在增函数,首先分析对数式y=lga中真数大于零,即a>0,同时要满足在增函数,说明了幂指数为正数,即1-lga>0,得到lga<1=lg10,a<10,这样结合a>0,可知实数a的取值范围是(0,10)。
【考点】本试题主要是考查了幂函数的单调性与幂指数的正负之间的关系的应用,属于基础题。
点评:解决该试题关键是理解幂函数在y轴右侧的单调性是增,说明了幂指数为正,如果在y轴右侧为减,说明幂指数为负数。
同时对数真数大于零是易忽略点。
5.设幂函数的图像经过点,设,则与的大小关系是()A.B.C.D.不能确定【答案】A【解析】因为幂函数的图像经过点,设因为图像经过点,所以,解得,所以在第一象限单调递减.因为,所以,所以.【考点】本小题主要考查幂函数的图象和性质,考查利用幂函数的单调性比较两个函数值的大小. 点评:幂函数的定义是形式定义,是形如的函数,当时,函数在第一象限单调递增.6.若函数是幂函数,则的值为()A.B.C.D.【答案】A【解析】函数是幂函数,则即。

高一数学指数与指数函数试题答案及解析1.设函数则使得成立的的取值范围是()A.B.C.D.【答案】C【解析】当时,由,可得,即;当时,由,可得,即,综上.故选C【考点】函数的求值.2.若,则在,,,中最大值是()A.B.C.D.【答案】C【解析】由指数函数的性质,得,;由幂函数的性质得,因此最大的是.【考点】指数函数和幂函数的性质.3.若函数有两个零点,则实数a的取值范围为【答案】【解析】研究函数与函数图像交点个数.当时,由于直线在轴的截距大于,所以函数与函数图像在及时各有一个交点. 当时,由于单调减,直线单调增,所以函数与函数图像只3在时有一个交点.【考点】指数函数图像4..【答案】【解析】原式=【考点】指数与对数5.设函数y=x3与的图像的交点为(x0,y),则x所在的区间是()A.(0,1)B.(1,2)C.(2,3)D.(3,4)【答案】B【解析】由函数知识知函数y=x3与的图像的交点为(x0,y)的横坐标x即为方程的解,也是函数函数=的零点,由零点存在性定理及验证法知<0,故x0在区间(1,2)内.由题知x是函数=的零点,∵==-7<0,故选B.【考点】函数零点与函数交点的关系,零点存在性定理6.函数在上的最大值比最小值大,则 .【答案】【解析】因为,根据指数函数的性质可知在单调递增,所以最大值为,最小值为,依题意有即,而,所以.【考点】指数函数的图像与性质.7.已知指数函数(且)的图像过点,则实数___________.【答案】【解析】因为指数函数(且)的图像过点,则,得.【考点】指数函数的定义.8.设,且,则= ( )A.100B.20C.10D.【答案】A【解析】由题设,得,则,同理有,又,得,即,所以.故正确答案为A.【考点】指数式、对数式的运算9.函数在区间[0,1]上的最大值和最小值之和为.【答案】4【解析】因为在[0,1]上单调递增,在[0,1]上单调递减,所以在 [0,1]单调递增,所以y的最大值为,最小值为,所以最大值和最小值之和为4.【考点】指数函数和对数函数的单调性及利用单调性求最值10. (1)计算:(2)已知,求的值.【答案】(1);(2).【解析】(1)此题主要考查学生对指数运算法则、对数运算性质的掌握情况,以及对指数式、对数式整体与局部的认识,属基础题;(2)经过审题,若从已知条件中求出难度较大,由指数运算法则知,,所以所求式子中的,. 试题解析:(1)原式= 6分(2)因为得得所以原式= 12分【考点】1.指数运算法则;2.对数运算性质.11.(1)求的值;(2)求的值.【答案】(1);(2).【解析】(1)初中所学单项式与多项式的运算法则和乘法公式,当指数变成分数时仍然适用;(2)对数的运算一般要转化为同底数的对数才能运用对数的运算法则.试题解析:(1);(2)原式=.【考点】(1)指数的运算;(2)对数的运算.12.集合A是由适合以下性质的函数构成的:对于定义域内任意两个不相等的实数,都有.(1)试判断=及是否在集合A中,并说明理由;(2)设ÎA且定义域为(0,+¥),值域为(0,1),,试写出一个满足以上条件的函数的解析式,并给予证明.【答案】(1),;(2)【解析】(1)根据题目给出的性质对函数与进行判断即可;(2)可以模仿(1)中的函数进行寻找,或者可以这么找,因为我们学了指数、对数、幂函数,而(1)中已经出现了对数函数与幂函数,所以是否可以考虑从指数函数中寻找.试题解析:(1),. 2分对于的证明. 任意且,即. ∴ 4分对于,举反例:当,时,,,不满足. ∴. 7分⑵函数,当时,值域为且. 9分任取且,则即. ∴. 14分【考点】1.函数性质;2.新定义型解答题;3.指数函数、对数函数、指数函数.13.三个数的大小关系为()A.B.C.D.【答案】D【解析】,,,故,选D.【考点】指数、对数函数性质.14.已知函数(1)若存在,使得成立,求实数的取值范围;(2)解关于的不等式;(3)若,求的最大值.【答案】(1)(2);②;③,,(3)【解析】(1)令,即成立 1分的最小值为0,当时取得 4分5分(2),令 6分① 7分② 8分③ⅰ 9分ⅱ 10分(3)令则12分13分,的最大值为 14分【考点】二次函数点评:主要是考查了二次函数的最值以及不等式的性质的运用,属于基础题。

书山有路勤为径;学海无涯苦作舟
高一数学2.2.1分数指数幂练习题(带答案)
数学必修1(苏教版)
2.2指数函数
2.2.1分数指数幂
在初中我们已经知道:若x2=a,则x叫做a的平方根,同理,若
x3=a,则x叫做a的立方根.根据平方根、立方根的定义,正实数的平方根有两个,它们互为相反数,如4的平方根为±2,负数没有平方根,
一个数的立方根只有一个,如-8的立方根为-2;零的平方根、立方根均为零,那幺类比平方根、立方根的概念,n次方根的概念是什幺呢?
基础巩固
1.下列各式中,对x∈R,n∈N*恒成立的是()
A.nxn=x
B.n|x|n=x
C.(nx)n=x D.2nx2n=|x|
解析:nxn=x,n为奇数|x|,n为偶数.
答案:D
2.设a=424,b=312,c=6,则a,b,c的大小关系是()
A.a>;b>;c B.bC.b>;c>;a D.a
专注下一代成长,为了孩子。



n 次方根与分数指数幂同步练习一、选择题1. 若2m ⋅4n =16,则必有( )A. mn =4B. mn =2C. m +2n =2D. m +2n =42.√a 55+√(2a −1)44的化简结果为()A. 1−aB. 3a −1C. 1−a 或3a −1D. a −1或1−3a3. 当x >0时,若√√x 3=3x,则x =( )A. 927B. 327C. 925D. 3254. 若{1,a,ba }={0,a 2,a +b },则a 2012+b 2012的值为( )A. 0B. 1C. −1D. 1或−15. 若10a =5,10b =2,则a +b =( )A. −1B. 0C. 1D. 26. 已知a m =4,a n =3,则√a m−2n 的值为()A. 23B. 6C. 32D. 27. 化简√√ab 23⋅a 3b 2√b 3⋅(a 16b 12)4(a,b 为正数)的结果是( )A. baB. abC. abD. a 2b8. 有下列说法:①81的4次方根是3;②√164的运算结果是±2;③当n 为大于1的奇数时,√a n对任意a ∈R 都有意义; ④当n 为大于1的偶数时,√a n只有当a ⩾0时才有意义.其中,正确的是( )A. ①③④B. ②③④C. ②③D. ③④9. 若xy ≠0,那么等式√x 2y 3=−xy √y 成立的条件是A. x >0,y >0B. x >0,y <0C. x <0,y >0D. x <0,y <010. 已知a =0.24,b =0.32,c =0.43,则()A. b <a <cB. a <c <bC. c <a <bD. a <b <c二、填空题11. 化简(a 23b 12)(−3a 12b 13)÷(13a 16b 56)的结果是____.12. 化简:√(−4)44=__________. 三、解答题 13. (1)计算0.027−13−(−16)−2+810.75+(19)0−3−1;(2)若x 12+x −12=√6,求x+x −1−1x 2+x −2−2的值.14. 求下列各式的值:(1)√10044; (2)√(−0.1)55; (3)√(π−4)2; (4)√(x −y)66.15. (1)求值:(214)12−(−9.6)0−(338)−23+1.5−2+[(−5)4]14;(2)已知a 12+a −12=3,求a 32+a −32的值. (附:a 3+b 3=(a +b)(a 2−ab +b 2))答案和解析1.D【解答】解:∵2m ⋅4n =2m ⋅22n =2m+2n =24, ∴m +2n =4.2.C解:√a 55+√(2a −1)44=a +|2a −1|={1−a,a <123a −1,a ≥12,故√a 55+√(2a −1)44的化简结果为1−a 或3a −1.3.A解:∵√√x 3=3x,∴√x 3=9x 2,∴x 2⋅x 32=x 72=9, ∴x =927.4.B解:根据题意,对于{a,ba ,1},有a ≠1,a ≠0; 又有{1,a,ba }={0,a 2,a +b }, 则有a =0或b a =0; 又由a ≠0;故b =0;代入集合中.可得{a,1,0}={a 2,a ,0}, 必有a 2=1, 又由a ≠1, 则a =−1;则a 2012+b 2012=1.5.C解:10a =5,10b =2,所以10a ·10b =10a+b =5×2=10, a +b =1,6.A解:√a m−2n =√a m (a n )2=√49=23.7.C解:原式=[(ab 2)13⋅a 3⋅b 2]12b 13⋅a 23⋅b 2=(a 13+3·b 23+2)12a 23·b 13+2=(a 103·b 83)12a 23·b 73=a 103×12−23·b 83×12−73=a ·b −1=ab.8.D解:①81的4次方根是±3,故①错误;②√164的运算结果是2,故②错误;③当n 为大于1的奇数时,√a n对任意a ∈R 都有意义,故③正确;④当n 为大于1的偶数时,√a n只有当a ⩾0时才有意义,故④正确.9.C解:∵xy ≠0,且√x 2y 3=−xy √y , ∴y >0,xy <0, 则y >0,x <0,10.B解:∵c =0.43=0.064,a =0.24=0.0016, ∴a <c ,又∵c =0.43=0.064,b =0.32=0.09,c <b , ∴a <c <b ,11.−9a解:(a 23b 12)(−3a 12b 13)÷(13a 16b 56)=−9a 23+12−16b 12+13−56=−9a .12.4解:根据偶次方根的性质得√(−4)44=|−4|=4. 故答案为4.13.解;(1)原式=0.33×(−13)−1(−16)2+34×0.75+1−13=103−36+27+1−13=−5.(2)若x 12+x −12=√6,两边平方得x +x −1=4, 再两边平方得x 2+x −2=14,故x+x −1−1x 2+x −2−2=4−114−2=14.14.解:(1)√10044=10044=1001=100; (2)√(−0.1)55=(−0.1)55=(−0.1)1=−0.1;;(4)√(x −y)66=|x −y |.15.解:=32−1−49+49+5 =112;(2)∵a 12+a−12=3,∴a 32+a −32=(a 12)3+(a −12)3=(a 12+a −12)(a +a −1−1), ∵(a 12+a −12)2=9=a +a −1+2,所以a +a −1=7,代入上式得,a 32+a −32=3×(7−1)=18.。

第二章 2.1 2.1.1 第二课时基础巩固一、选择题1.下列各式中正确的是( ) A.6(-2)2=(-2)13B.4x 3y 3=xy 34(x >0,y >0) C.3a 2-b 2=a 13-b 13D.3x y =(y x )-13(x ≠0,y ≠0) [答案] D2.将532 写成根式,正确的是( )A.352B.35C.532D.53 [答案] D3.5a -2可化为( )A .a -25B .a 52C .a 25D .-a 52 [答案] A4.(-x )2·-1x等于( ) A.xB .-x ·-xC .x ·xD .x ·-x [答案] B[解析] 由-1x 知x <0,又当x <0时,x 2=|x |=-x ,因此(-x )2-1x =x 2·-x |x |=-x ·-x ,故选B.5.若a 12 +a -12 =5,则aa 2+1的值为( )A.15B.123C.125D.127[答案] B[解析] ∵a 12 +a -12 =5,a >0, ∴a +1a =5,(a +1a )2=25, ∴a +1a =23,∴a a 2+1=1a +1a=123,故选B.6.(2015·黑龙江哈尔滨三中期中)化简a 23 b 12 (-3a 12 ·b 13 )÷(13a 16 b 56 )的结果为() A .9a B .-9aC .9bD .-9b[答案] B[解析] 原式=(-3)×3a 23 +12 -16 b 12 +13 -56 =-9ab 0=-9a .二、填空题7.(2015·广西桂林中学段考)2723 +16-12 -(12)-2-(827)-23 =________.[答案] 3[解析] 原式=(33) 23 +(42)-12 -22-[(23)3]-23 =32+4-1-4-94=3.8.(2015·山东月考)化简:(1-a )·41(a -1)3=________.[答案] -4a -1[解析] 要使原式有意义,需a -1>0.(1-a )41(a -1)3=(1-a )(a -1)-34 =-(a -1)(a -1) -34 =-(a -1) 14 =-4a -1.三、解答题9.求下列各式的值:(1)2532 ; (2)(254)-32 ; (3)33×43×427.[解析] (1)2532 =(52) 32 =53=125.(2)(254)-32 =[(52)2]-32 =(52)-3=8125. (3)33×43×427=313 ×314 ×334 =333. 10.计算下列各式:(1)(279 )0.5+0.1-2+(21027)-32 +3748; (2)(a -2b -3)(-4a -1b )÷(12a -4b -2c );(3)a -2-b -2a -1+b-1+(-a 12 -b -12 )(a 12 -b -12 ). [分析] 负化正、大化小,根式化为分数指数幂,小数化为分数,是简化运算的常用技巧.[解析] (1)原式=(259)12 +10.12+(6427)-23 +3748=53+100+916+3748=103. (2)原式=-13a -2-1-(-4)b -3+1-(-2)c -1 =-13ac -1=-a 3c. (3)原式=1a 2-1b 21a +1b+(-b -12 )2-(a 12 )2 =a -1-b -1-a +b -1=1a -a =1-a 2a. [点评] 一般地,进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数为分数进行运算.能力提升一、选择题1.(2015·浙江期中)下列各式正确的是( )A .a -35 =13a 5B.3x 2=x 32C .a 12 a 14 a -18 =a 12 ×14 ×(-18 )D .2x -13 (12x 13 -2x -23 )=1-4x[答案] D[解析] 13a 5=1a 53=a -53,故A 错;3x 2=x 23 ,故B 错;a 12 a 14 a -18 =a 12 +14 -18 ,故C 错;D 正确.2.(112)0-(1-0.5-2)÷(278)23 的值为( ) A .-13B.13C.43D.73 [答案] D[解析] 原式=1-(1-22)÷(32)2=1-(-3)×49=73,故选D. 3.计算(2a -3b -23 )·(-3a -1b )÷(4a -4b -53 )得( )A .-32b 2 B.32b 2 C .-32b 73 D.32b 73 [答案] A[解析] 原式=-6a -4b 134a -4b -53=-32b 2,故选A. 4.如果x =1+2b ,y =1+2-b ,那么用x 表示y 等于( )A.x +1x -1B.x +1xC.x -1x +1D.x x -1[答案] D[解析] y =1+2-b =1+12b =1+1x -1=x x -1,故选D. 二、填空题5.化简733-3324-6319+4333的结果是________. [答案] 0[解析] 733-3324-6319+4333=7×313 -3×313 ×2-6×3-23+(3×313 )14 =313 -6×3-23 +313 =2×313 -2×3×3-23 =2×313 -2×313 =0.6.已知a 2m +n =2-2,a m -n =28,a >0,且a ≠1,则a 4m+n 的值为________.[答案] 4 [解析] 因为⎩⎪⎨⎪⎧a 2m +n =2-2,①a m -n =28,②所以①×②得a 3m =26,所以a m =22. 将a m =22代入②得22×a -n =28,所以a n =2-6,所以a 4m +n =a 4m ×a n =(a m )4×a n =(22)4×2-6=22=4.三、解答题7.已知a 12 +a 12 =5,求下列各式的值:(1)a +a -1;(2)a 2+a -2;(3)a 2-a -2.[解析](1)将a 12 +a 12 =5两边平方,得a +a -1+2=5,则a +a -1=3. (2)由a +a -1=3两边平方,得a 2+a -2+2=9,则a 2+a -2=7.(3)设y =a 2-a -2,两边平方,得y 2=a 4+a -4-2=(a 2+a -2)2-4=72-4=45,所以y =±35,即a 2-a -2=±3 5.8.(2015·江苏盐城一中)(1)已知x =12,y =23,求x +y x -y -x -y x +y的值; (2)已知a 、b 是方程x 2-6x +4=0的两根,且a >b >0,求a -b a +b的值. [思路点拨] 若直接代入求解较繁,可以先化简再求值.(1)要分母有理化;(2)先将要求的式子平方,化成易于将条件代入的式子,最后求得结果.[解析] (1)x +y x -y -x -yx +y =(x +y )2x -y -(x -y )2x -y =4xy x -y . 当x =12,y =23时, 原式=412×2312-23=413-16=-2413=-8 3. (2)∵a ,b 是方程x 2-6x +4=0的两根,∴⎩⎪⎨⎪⎧ a +b =6,ab =4.∵a >b >0,∴a >b ,(a -b a +b )2=a +b -2ab a +b +2ab =6-246+24=15,∴a -b a +b =15=55.。
