MT大地电磁一维正演计算

实验报告课程名称：地电学课题名称：大地电磁层状模型数值模拟实验专业：地球物理学姓名：xx班级：06xxxx完成日期：2016 年11月26日目录一、实验名称 (3)二、实验目的 (3)三、实验要求 (3)四、实验原理 (3)五、实验题目 (4)六、实验步骤 (4)七、实验整体流程图 (8)八、程序及运行结果 (9)九、实验结果分析及体会 (14)一、实验名称大地电磁层状模型数值模拟实验二、实验目的（1）学习使用Matlab编程，并设计大地电磁层状模型一层，二层，三层正演程序（2）在设计正演程序的基础上实现编程模拟（3）MATLAB软件基本操作和演示.三、实验要求（1）利用MT一维测深法及其相关公式，计算地面上的pc视电阻率和ph相位，绘制视电阻率正演曲线和相位曲线并分析。

（2）利用Matlab软件作为来实现该实验。

四、实验原理（一）、正演的概念：正演是反演的前提。

在实际地球物理勘探中，一些模型的参数是不容易确定的，如埋藏在地下的地质体模型的岩性、厚度、产状等参数，我们把这些描述未知模型的参数的集合定义为“模型空间”。

为了获得这些模型参数，可以利用那些可以直接观测的量来推测，而这些能够直接观测的量的集合则被称作“数据空间”。

如果把模型空间中的一个点定义为m，把数据空间中的一个点定义为d，按照物理定律，可以把两者的关系写成式中，G为模型空间到数据空间的一个映射。

我们把给定模型m求解数据d的过程称为正演问题。

（二）、MT一维正演模型简介大地电磁法作为一种电磁类勘探方法，它的模型参数为一组能够表征地球物理勘探目标体的电性参数，即目标体电阻率和相应层的层厚度。

所谓一维模型，即介质在三维空间中沿两个方向上模型参数是不变的，只在另一个方向上特征属性会变化。

在此一维模型即指水平层状一维介质，即介质只在沿垂直于地面上的方向上电性（电阻率）变化，在另外两个方向上保持不变的典型特征，所以就构成一组电阻率不同的电性层，抽象出来即是一组由电阻率及对应的层厚度构成的电性层数。

WinGlink处理MT数据说明书WinGlink是一款意大利GEOSYSTE公司开发的综合解释平台，主要侧重于大地电磁的建模和数据处理，能结合重磁资料和大地电磁的联合处理解释，并实现了钻孔等资料的约束反演。

该系统实现了大地电磁的一、二维反演，并可进行三维大地电磁的模拟，其正演采用了Randy Mackie的二维交错采样有限差分迭代算法程序。

本文针对WinGlink处理大地电磁测深数据作详细的讲解。

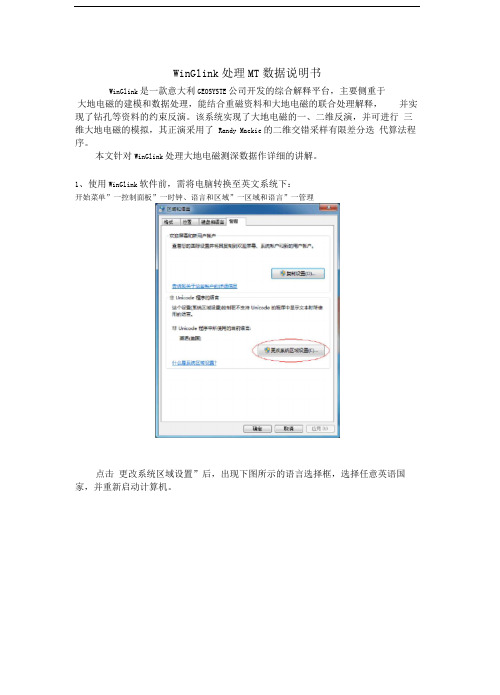
1、使用WinGlink软件前，需将电脑转换至英文系统下：开始菜单”一控制面板”一时钟、语言和区域”一区域和语言”一管理点击更改系统区域设置”后，出现下图所示的语言选择框，选择任意英语国家，并重新启动计算机。

2、重新启动后，点击图标运行软件，出现下图中的对话框:其中1号框图表示创建一个新的数据库；2号框图表示打开一个已有的数据库，3号框图则表示使用已购买的工具箱。

对于初学者或该软件为破解版的情况下，一般选择1号或者2号框图按钮。

本文中点击“cre a t newdatabase”，然后点击“0傲钮。

3、点击“0!按钮后，会弹出一存储对话框，选择存储的文件夹并编辑数据库名称。

4、新建数据库后，则需填写新建的数据库信息(Database properties)其中共三项，分别Gen era、Projected Coords Geographic Coords& Coordin^e^ UnihiKiomotersElevation UnitsMeJersHemisphereNorth第一项：Ge neral （常规信息），其中包含地区名称、所处半球，平面坐标单位、垂直坐标的单位。

第二项：ProjectedCoords （投影坐标），对话框中的UTM即Universal Transverse Mercato,表示通用横轴墨卡托投影，处理MT数据一般默认使用该投影，故无需进行改变。

中间的True Origin （坐标原点），Latitude框无法改变，而Longitude框的数值则需改成测区范围的任意经度，并以度分秒的形式，例如改写成：107°0'00.0000'。

文章编号:1672—7940(2006)01—0009—07大地电磁三维模型的一维二维反演近似问题研究陈小斌1,赵国泽1,马　霄2(1.中国地震局地质研究所,北京100029;2.大港油田集团石油工程监理中心,天津300280)作者简介:陈小斌(1972—),男,中国地震局地质研究所副研究员,主要从事电磁测深正反演方法及地球动力学数值模拟方面的研究。

E -mail :cxb @pku 1edu 1cn摘　要:设计了一个简单的三维模型———均匀半空间的三维低阻异常体模型。

采用51×51×38的网格计算得到了331333Hz 至010071Hz 之间共34个频率的三维正演响应。

选取其中5条具有代表性的测线,比较了不同测线上自适应正则化(ARIA )一维反演结果和非线性共轭梯度法(NL CG )二维反演结果相互之间及其与原三维理论模型之间的异同,研究大地电磁三维模型的一维、二维反演的近似情况。

发现:对于三维模型响应,一维、二维反演都能得到反映模型真实信息的结果,但二维模型对三维模型的近似程度比一维模型要高得多;在二维模型反演中,采用TM 模式更易得到真实的模型信息。

研究中,采用蒲兴华等(1994)开发的M T 三维正演程序进行正演计算,采用“大地电磁数据管理器(M TDA TAMN G )”软件进行数据处理和一维、二维反演。

关键词:大地电磁;三维;一维;二维;反演中图分类号:P631124文献标识码:A收稿日期:2005—12—18RESEARCH ON INVERSION OF MT3D MODE L APPR OXIMATE LY B Y 1D ,2D INVERSION METH ODC H EN Xiao 2bin 1,ZHAO Guo 2ze 1,MA Xiao 2(11I nstitute of Geolog y ,China Seismological B ureau ,B ei j ing 100029,China;21Dagang Pet roleum S u pervision Cent re ,Tianj ing 300280,China )Abstract :In t his paper ,a simple 3d model ,low -resistivity abnormity 3d model in halfspace ,is designed 1Responses of 34frequencies from 331333Hz to 010071Hz are obtained in3d modeling wit h 515138grids 15rep resentatio nal lines are adopted to st udy approxima 2ting 3d model wit h 1d ,2d inversion result s 1Result s of 1d inversion ,2d inversionfor each line are comp uted ,and are compared wit h each ot her and wit h t he original model 1St udies show t hat bot h 1d and 2d inversion result s contain t rue 3d model information ,but t he 2d inversion is far more app roached to 3d model t han 1d inversio n 1Furt hermore ,when app roaching 3d models wit h 2d inversion ,it is t he TM polarization modedata rat her t han t he TE polarization mode data t hat sho uld be adopted 1The 3d modelingprogram used in t his paper was developed by Dr 1PU Xinghua 1The new visual integratedsystem ,M TDA TAMN G ,is used in data processing and inversion 1The 1d inversion met h 2第3卷第1期2006年2月 工程地球物理学报CHIN ESE J OU RNAL OF EN GIN EERIN G GEOP H YSICS Vol 13,No 11Feb 1,2006od is adaptive regularized inversion algorit hm(A RIA),and2d inversion met hod is nonlin2 ear conjugate gradient s algorit hm(NL C G)1K ey w ords:M T;3d;1d;2d;inversion1　引　言当前,大地电磁测深的一维和二维反演技术已相对成熟,并成为实际资料处理和解释中的主要手段。

大地电磁一维正反演MATLAB程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%% Purpose:MagnetoTelluric one dimensional forward modeling %% Ming-Cai ZHang 17st,OCt,2008 CSU-IPGE % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%% variable declaration %% Input: %% 1、n---->>>The number of layer %% 2、rou-->>>Density for every layer %% 3、h---->>>Thickness for every layer %% 4、T_start---->>>start time %% 5、T_end----->>>end time %% 6、Num_DT-->>the number of sampling time in time interval %% Output: %% 1、rou_T-->>apparent resistivity at time % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%function [T,rou_T]=mt1d(n,rou,h,T_start,T_end,Num_DT) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%% Control subjacent variable to build model %%n=2; %%rou(1:n)=[200,600]; %%h(1:(n-1))=10; %% Control subjacent variable to change continued time %%T_start=-3; %%T_end=4; %%Num_DT=5; % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%np=nargin;if (np<=5)error('******正演参数不够******！')endu(1:n)=1;v(1:n)=0;j=0;T=zeros(1,(T_end-T_start+1)*Num_DT);for t=T_start:1:T_endT1=linspace(10^t,10^(t+1),Num_DT);for i=1:1:Num_DTj=j+1;T(j)=T1(i);endendfor j=1:1:(T_end-T_start+1)*Num_DTfor m=(n-1):-1:1[P(m+1),Q(m+1)]=set_pqm1(rou(m+1),rou(m),u(m+1),v(m+1));G(m)=(4*3.14159265*h(m))/sqrt(10*rou(m)*T(j));e_G(m)=exp(-G(m));[A(m),B(m)]=set_ABm(P(m+1),Q(m+1),G(m),e_G(m));u(m)=(1-(A(m))^2-(B(m))^2)/((1+A(m))^2+B(m)^2);v(m)=-2*B(m)/((1+A(m))^2+B(m)^2);endrou_T(j)=rou(1)*(u(1)^2+v(1)^2);endfigure(1)picture1=plot(log10(T),(rou_T),'--*r','MarkerFaceColor','k','MarkerSize',10); %picture1=plot(log10(T),(rou_T),'--rs','LineWidth',2,...%'MarkerEdgeColor','k',...%'MarkerFaceColor','b',...%'MarkerSize',5);warndlg('请保存正演数据，方便以后利用！！');pathname='e:\mt1d';outfile1=fullfile(pathname,'forward.txt');fid=fopen(outfile1,'w');fprintf(fid, '%s\n','T Log(T) Resitivity');for i=1:1:length(T)fprintf(fid,'%6.2f %12.8f %12.8f\n',T(i),log10(T(i)),rou_T(i));endfclose(fid);function [Am,Bm]=set_ABm(Pm1,Qm1,Gm,e_Gm)Am=e_Gm*(Pm1*cos(Gm)-Qm1*sin(Gm));Bm=e_Gm*(Qm1*cos(Gm)+Pm1*sin(Gm));function [pm1,qm1]=set_pqm1(roum1,roum,um1,vm1)a1=(sqrt(roum1/roum)*um1);a=a1^2;b1=(sqrt(roum1/roum)*vm1);b=b1^2;pm1=(1-a-b)/((1+a1)^2+b);qm1=(-2*b1)/((1+a1)^2+b);function dif(x)[T,rou]=mt1d(5,[5,10,15,10,5],[10,20,30,100],-3,6,20);log_rou=log10(rou);log_T=log10(T);log_omeg=log10(2*3.14159265./T);for i=2:1:length(T)-1d_log_rou(i)=log_rou(i+1)-log_rou(i-1);d_log_T(i)=log_T(i+1)-log_T(i-1);d_log_omeg(i)=log_omeg(i+1)-log_omeg(i-1);a(i)=(d_log_rou(i))/(d_log_T(i));fai(i)=(d_log_rou(i))/(d_log_omeg(i));enda(1)=(log_rou(2)-log_rou(1))/(log_T(2)-log_T(1));a(length(T))=(log_rou(length(T))-log_rou(length(T)-1))/(log_T(length(T))-log_T(length(T)-1)); fai(1)=(log_rou(2)-log_rou(1))/(log_omeg(2)-log_omeg(1));fai(length(T))=(log_rou(length(T))-log_rou(length(T)-1))/(log_omeg(length(T))-log_omeg(length( T)-1));bsdk_rou=rou.*((1+a)./(1-a));bsdk_d=rou.*T;bsdk_d=bsdk_d/(8*(pi^2)*10^(-7));bsdk_d=sqrt(bsdk_d);bsdk_d=sqrt((rou.*T)./(8*(pi^2)*10^(-7)));s=bsdk_d./rou;hold onplot(log10(T),bsdk_rou,'--ks','MarkerFaceColor','k','MarkerSize',10);figure(2)plot(log10(bsdk_rou),log10(bsdk_d),'--ks','MarkerFaceColor','k','MarkerSize',10);。

《电法资料处理与解释》MT二维正演计算学院：地质工程与测绘学院专业：勘查技术与工程指导老师：姓名：学号：完成时间：2017.12.20二〇一七年十二月一、实验目的1.了解大地电磁法的二维正演理论；2.理解大地电磁二维张量阻抗的概念；3.理解电性主轴、TE模式、TM模式的概念；4.通过对二维地电模型的计算，断面图的绘制，理解二维地电模型的视电阻率和视相位特征，对TE模式和TM模式的特点及分辨率有较好的理解。

二、实验要求1.能够正确应用二维大地电磁模拟软件进行建立模型，网格剖分合理，频率选择范围合适；2.对相关模型进行计算，并绘制视电阻率断面图，视相位断面图，并对结果进行分析；3.完成实验报告，word排版，图标清晰，分析合理。

三、实验内容1.均匀半空间模型模拟，与一维解析解进行比较，并进行精度对比；2.建立单个低阻体、高阻体地电模型进行计算；3.建立地堑或地垒等复杂地典模型模拟；4.建立多个异常体进行模拟。

四、实验原理二维介质是指介质的电学性质除沿深度方向上变化外，还沿一个水平方向上有变化，而沿另一个方向保持不变，这个方向称为走向。

计算二维介质的大地电磁场—阻抗—视电阻率和相位的过程成为二维大地电磁正演。

二维介质波阻抗一维、二维波阻抗区别：故二维介质的波阻抗为张量阻抗，即：电性主轴是一个假定的主轴是因为非均匀大地里面存在各向异性，为了使得测线所测得电阻率充分反映各向电阻率差异，根据地质体的走向定义电性主轴，将测量的视电阻率按照主轴方向进行旋转分解，得到沿主轴方向的参数。

五、结果及分析（一）软件特性检验1.均匀半空间将均匀半空间一维正演程序结果曲线与此二维软件结果对比如图5.1.1和图5.1.3，均匀半空间视电阻率值为一定值，二者基本符合，二维软件具有边界效应，-10001004648505254m•s Ω/ρ图5.1.1均匀半空间一维正演程序s 曲线使得近地表有稍许扰动，但整体为定值50。

从而验证软件特性较好。

实验报告实验名称：实验三MT二维正演计算实验四MT反演计算课程名称: 电法勘探专题实验时间：2011年12月8日学号：2602080206姓名：黄建华任课老师：张继锋目录实验三MT二维正演计算 (1)一、实验目的 (1)二、实验要求 (1)三、实验内容 (1)四、结果及分析 (2)(一)、软件特性检验 (2)(二)、单个高阻体下Eps、Mps断面对比，Eh、Mh断面对比 (4)(三)、单个低阻体TE模式视电阻率断面 (5)(四)、横向分辨率分析(两个相同大小地质体的分辨) (5)(五)、纵向分辨率分析 (6)(六)、倾斜断层TE模式视电阻率和视阻抗相位断面 (6)(七)、地堑地电模型TE模式视电阻率和视阻抗相位断面 (7)实验四MT反演计算 (9)一、两层介质 (9)二、三层介质（第一层厚度10） (10)三、三层介质（第一层厚度50） (12)四、五层介质 (13)五、总结 (13)实验三MT二维正演计算一、实验目的1、掌握大地电磁法的二维有限元正演理论2、明确TE极化模式和TM极化模式特征3、编制二维正演程序（参考徐世浙有限元与边界元）4、掌握二维反演软件的应用，理解网格剖分的规则，合理的进行网格剖分和模型计5、设计不同的二维地电模型，包括一维层状模型进行程序精度的检验，分别就TE和TM模式进行正演，并根据结果分析两种模式的异同。

二、实验要求1、能够正确应用软件，掌握各参数的设置2、了解软件设计的基本思路，能够自己调整修改相关输出输入参数3、对设计模型进行计算，并绘制相关误差分析剖面曲线，进行误差统计，并对模拟结果做以分析。

4、完成实验报告，word排版，图标清晰，分析合理。

三、实验内容1、均匀半空间及层状介质模型模拟，并和一维正演程序进行比较，分析误差，以检验二维正演软件的正确性。

2、设计一个低阻体和高阻体分别就TE和TM模式进行正演3、设计一个倾斜断层模型4、设计一个地堑地电模型5、其他模型四、结果及分析(一)、软件特性检验 1. 均匀半空间将均匀半空间一维正演程序结果曲线与此二维软件结果对比如图1，均匀半空间视电阻率值为一定值，二者基本符合，二维软件具有边界效应，使得近地表有稍许扰动，但整体为定值50 。