多电子波函数理论ppt
- 格式:ppt
- 大小:2.69 MB
- 文档页数:38

波函数及其统计解释一、波函数i2()0(,)t x x t e,h p E hi()0(,)Et px x t e/2hi2()(,)t x y x t Ae复数形式(取实部)对于动量为p , 能量为E 的自由粒子i ()0(,)Et p r r t e自由粒子波函数自由粒子可用平面简谐波描述(,)cos 2()y x t A t x 平面简谐波:一维自由粒子波函数是波函数的振幅。
注意:微观粒子物质波的波函数只能用复数形式来表达。
不能用实数形式来表达。
量子力学假设:粒子的状态用波函数描述。
(,)r t*为 的复共轭函数。
根据波动理论,波函数的强度正比于 02。
利用复指数函数的运算法则,有:||220*物质波的波函数表示什么?(r ,)t对于机械波y (x ,t )代表位移;对于电磁波y (x ,t ) 代表电场强度或磁场强度。
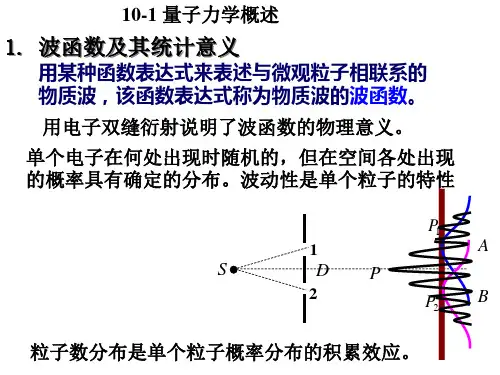
照相底片上某点附近干涉图样的强度该点附近感光点的数目该点附近出现的电子数电子出现在该点附近的概率,即dN/N照相底片上某点干涉图样的强度电子出现在该点的概率密度,即dN/(NdV ) (r ,t )21926年6月玻恩(M.Born )提出的波函数的统计解释。
波函数在空间某点的强度(波函数模的平方)与粒子在该点出现的概率密度成正比。
dN(r,t )N dV2 二、概率密度1954诺贝尔物理学奖M.玻恩(Max Born 1882~1970)对量子力学的基础研究,特别是量子力学中波函数的统计解释dN wr ,t ==C (r ,t )NdV()2概率密度:*dW wdV=C dV C dV2体积元dV 内出现的概率:*V V V W dW C dV C dV2体积V 内出现的概率:wdV C dV 21如果C =1,归一化条件dN w(r,t )(r,t )NdV2归一化的波函数:C 是比例系数C dV 21(1)dV=1 2(3)w C dV222(2)粒子在整个空间出现的概率波函数又称为概率幅。









多电子原子的波函数描述和角动量理论在原子物理学中,多电子原子是指具有多个电子的原子系统。
为了描述和理解多电子原子的性质和行为,科学家们提出了波函数描述和角动量理论。
本文将探讨这两个重要概念在多电子原子中的应用。
一、波函数描述波函数是量子力学中描述微观粒子状态的数学函数。
对于多电子原子,波函数描述了每个电子的位置和运动状态。
多电子原子的波函数可以通过Hartree-Fock方法或密度泛函理论等计算方法得到。
波函数的形式是由薛定谔方程决定的。
薛定谔方程是描述微观粒子的运动和行为的基本方程。
对于多电子原子,薛定谔方程可以写成如下形式:HΨ = EΨ其中,H是原子的哈密顿算符,Ψ是波函数,E是能量。
通过求解这个方程,可以得到多电子原子的波函数和能级。
在多电子原子中,波函数的形式可以通过一组基函数的线性组合得到。
这些基函数可以是Slater行列式、分子轨道或自旋轨道等。
波函数的形式决定了电子的空间分布和运动状态。
二、角动量理论角动量是描述物体旋转和自旋的物理量。
在多电子原子中,电子的角动量对于原子的性质和行为具有重要影响。
角动量理论可以帮助我们理解多电子原子的能级结构和光谱现象。
在量子力学中,角动量是由角动量算符表示的。
对于多电子原子,总角动量算符可以表示为L = L1 + L2 + ... + Ln,其中L1、L2、...、Ln是每个电子的角动量算符。
角动量算符具有一些重要的性质,如对易关系和本征值问题。
通过求解角动量算符的本征值问题,可以得到多电子原子的角动量量子数和角动量的取值范围。
多电子原子的角动量量子数包括轨道角动量量子数l和自旋角动量量子数s。
轨道角动量量子数决定了电子在原子中的运动方式,而自旋角动量量子数决定了电子的自旋状态。
根据角动量理论,多电子原子的能级结构可以分为不同的能级和能级分裂。
这些能级和能级分裂对应着原子的光谱线和光谱现象。
通过观察和研究原子的光谱,科学家们可以推断出原子的内部结构和电子的行为。
第三章 多电子波函数3.1 电子问题——对于一个N 电子,M 核的体系,在原子单位下,哈密顿Hamiltonian ,可以写为:221111111221NM N Mi AA i A i A A iAN NM MA B i j iA B A ij ABZ H M r Z Z r r =====>=>∇=--∇-++∑∑∑∑∑∑∑∑其中A M 是核A 相对于电子的约化质量A Z 为核A 的原子数第一项为电子动能项 (算符) 第二项为核动能项第三项为电子与核相互作用能 第四项为电子与电子相互作用能 第五项为核之间的相互作用能——为了使问题简化,Born Oppeheimer 提出假设(B O Approach ) 利用BO 近似,可以将核与电子运动分离,从而使我们只讨论电子问题,解决了电子问题后,我们还可以接着解决核问题。
——具体看一下BO 近似上式中,由于核与电子相比,质量很大,因此由动量守恒,其运动与电子相比就慢很多。
这样就可以假设电子是在由定核构成的场中运动。
因此:第二项: 核动能项可以忽略 第五项: 核排斥能为常数由于常数加在算符上,只改变算符本征值而不改变本征函数,因此,我们可以从总Hamiltonian 中减掉它,得到电子哈密顿,或描述N 电子在M 点电荷场中的哈密顿:21111112NN MN N A eleci i A i j i i iA ijZ H r r ====>=-∇-+∑∑∑∑∑其相对应的Schrodinger 方程为:elec elec elec elec H εΦ=Φ这时的Hamiltonian 的本征值不是多电子体系的总能。
为了求得体系总能量,我们需要加上1M MA BA B A ABZ Z r =>∑∑一项,我们以后只考虑电子问题,因此省略掉下标“elec ”。
由于电子Hamiltonian 含有双粒子坐标项11N Ni j i ijr =>∑∑,因此不能简单地利用变量分离法求解,只能用近似法求解。
多电子原子的波函数对称性在原子结构研究中,波函数对称性是一个重要的概念。
对于多电子原子而言,它涉及到电子的排布和角动量的分布。
本文将介绍多电子原子的波函数对称性以及其相关的性质和应用。
一、多电子原子的波函数多电子原子的波函数可以用来描述原子中电子的运动状态。
在研究多电子原子波函数时,我们需要考虑到电子之间的相互作用以及电子自旋的影响。
根据波函数的对称性,我们可以将波函数分为对称和反对称两类。
1. 对称波函数对称波函数又称为多电子原子的Singlet态。
在对称波函数中,多个电子之间的排布满足波函数的对称性要求。
换句话说,无法通过交换电子的位置来改变波函数的形式。
对称波函数常常用来描述处于基态的多电子原子。
2. 反对称波函数反对称波函数又称为多电子原子的Triplet态。
在反对称波函数中,多个电子之间的排布满足波函数的反对称性要求。
即通过交换电子的位置可以改变波函数的形式。
反对称波函数常常用来描述激发态的多电子原子。
二、多电子原子波函数的性质多电子原子的波函数具有一些重要的性质,这些性质直接影响着多电子原子的电子结构和化学性质。
1. Pauli不相容原理根据Pauli不相容原理,同一个原子中的电子不能具有完全相同的四个量子数。
这意味着同一能级上的电子必须具有不同的自旋状态,其中一个自旋为正,另一个为负。
这也导致了多电子原子的波函数的反对称性。
2. 电子排斥效应多电子原子中的电子具有相同的电荷,它们之间会发生排斥作用。
这种排斥效应导致电子更倾向于占据不同的空间轨道,从而实现电子的分布。
3. 约束性多电子原子的波函数还具有约束性,即电子的位置和动量不能完全确定。
这是由于电子存在于原子核的势能场中,受到核吸引和电子排斥的双重作用,使得电子的分布呈现一定的模糊性。
三、多电子原子波函数的应用多电子原子的波函数对称性及其相关的性质在原子结构的研究中具有广泛的应用。
1. 原子结构分析通过研究多电子原子的波函数对称性,我们可以了解到原子中电子的排布和角动量的分布。