二阶系统的性能指标
- 格式:docx
- 大小:59.80 KB
- 文档页数:2

机械工程控制基础29_二阶系统的性能指标二阶系统是指具有两个自由度的机械工程控制系统。
在控制系统理论中,衡量系统性能的指标有许多,比如超调量、调节时间、稳态误差等。
下面将详细介绍二阶系统的性能指标。
一、超调量:超调量是指过渡过程中输出量超过稳态值的最大偏离量。
对于二阶系统而言,其超调量可以通过过冲幅值与稳态值的差进行计算。
具体公式如下:超调量(%)=(过冲幅值-稳态值)/稳态值×100超调量主要反映了系统在过渡过程中的动态性能,是指标中最容易获取的。
二、调节时间:调节时间是指系统输出量从初始稳态值到达稳态值所需要的时间。
对于二阶系统而言,其调节时间通常从过渡过程的时间t1开始计算。
具体公式如下:调节时间=t2-t1其中,t2表示系统输出量进入超定态的时刻。
三、上升时间:上升时间是指系统输出量从初始稳态值到达稳态值所需要的时间,也即是调节时间的一部分。
对于二阶系统而言,上升时间是系统输出量从过渡过程的时间t1到达过冲幅值和稳态值之间的时间间隔。
四、峰值时间:峰值时间是指系统输出量达到过冲幅值或者偏离过冲幅值最远的时刻。
对于二阶系统而言,峰值时间是系统从过渡过程的时间t1到达过冲幅值的时间间隔。
五、稳态误差:稳态误差是指系统输出量在稳态下与期望输入量之间的偏差。
对于二阶系统而言,稳态误差可以通过比较系统稳态值与期望输入量来计算。
稳态误差主要反映系统的静态性能,也即系统对于不同输入的输出表现。
综上所述,二阶系统的性能指标主要包括超调量、调节时间、上升时间、峰值时间和稳态误差。
这些指标可以通过理论计算、仿真分析和实验测试等方法来获取,用于评估和比较不同二阶系统的控制性能。
在实际应用中,根据具体需求和控制要求,可以通过调整系统参数和控制策略等来改善系统的性能指标,并使系统能够更好地满足要求。

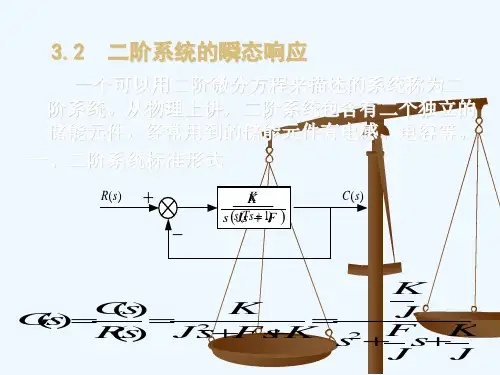
一、二阶系统传递函数的标准形式二阶系统的闭环传递函数写成标准形式为:2222)()(nn ns s s R s C ωξωω++=式中,ξ为阻尼比;n ω为无阻尼自振频率。
所以,二阶系统的特征方程为:022=++n n s s ωξω由上式解得二阶系统的二个特征根(即闭环极点)为:22.11ξωξω-±-=n n j s 随着阻尼比ξ取值的不同,二阶系统的特征根(即闭环极点)也不相同。
二、单位阶跃函数作用下二阶系统的过渡过程(针对欠阻尼状态,10<<ξ )令)(1)(t t r =,则有s s R 1)(=,二阶系统在单位阶跃函数作用下输出信号的拉氏变换为:2222222)()(1))((2112)(d n d d n d n n d n d n n n n n s s s s j s j s s s ss s s C ωξωωωξωωξωξωωξωωξωξωωξωω++⋅-+++-=-++++-=⋅++=式中,21ξωω-=n d 为有阻尼自振频率对上式进行反拉氏变换,得:)sin(11)sin 1(cos 1sin cos 1)(22ϕωξωξξωωωξωωξωξωξωξω+--=-+-=⋅--=----t e t t e t e t e t c d t d d t d td n d t n nnn式中,ξξϕ21-=arctg由上式看出,对应10<<ξ时的过渡过程,)(t c 为衰减的正弦振荡曲线.其衰减速度取决于ϕ角的定义n ξω值的大小,其衰减振荡的频率便是有阻尼自振频率d ω,即衰减振荡的周期为:2122ξωπωπ-==n dd T三、二阶系统的性能指标1.上升时间tr:上升时间是响应曲线由零上升到稳态值所需要的时间。
根据定义,当r t t =时,1)(=r t c 。
即 0sin 1cos 2=-+r d r d t t ωξξω或 nn r d t tg ξωξωω21-=,)(ϕπω-=tg t tg r d所以,上升时间为:21ξωϕπ--=n r t2.峰值时间tp:过渡过程曲线达到第一个峰值所需的时间。




邢台学院物理系《自动控制理论》课程设计报告书设计题目:二阶系统的性能指标分析专业:自动化班级:学生姓名:学号:指导教师:2013年3 月24 日邢台学院物理系课程设计任务书专业:自动化班级:2013年3 月24 日摘要二阶系统是指由二阶微分方程描述的自动控制系统。
例如,他励直流电动机﹑RLC电路等都是二阶系统的实例。
二阶系统的性能指标分析在自动控制原理中具有普遍的意义。
控制系统的性能指标分为动态性能指标和稳态性能指标,动态性能指标又可分为随动性能指标和抗扰性能指标。
稳态过程性能稳态误差是系统稳定后实际输出与期望输出之间的差值本次课程设计以二阶系统为例,研究控制系统的性能指标。
关键词:二阶系统性能指标稳态性能指标动态性能指标稳态误差调节时间目录1.二阶系统性能指标概述 (1)2. 应用模拟电路来模拟典型二阶系统。
(1)3.二阶系统的时间响应及动态性能 (4)3.3.1 二阶系统传递函数标准形式及分类 (4)3.3.2 过阻尼二阶系统动态性能指标计算 (5)3.3.3 欠阻尼二阶系统动态性能指标计算 (7)3.3.4 改善二阶系统动态性能的措施 (14)4. 二阶系统性能的MATLAB 仿真 (18)5 总结及体会 (19)参考文献 (19)1.二阶系统性能指标概述二阶系统是指由二阶微分方程描述的自动控制系统。
例如,他励直流电动机﹑RLC 电路等都是二阶系统的实例。
二阶系统的性能指标分析在自动控制原理中具有普遍的意义。
控制系统的性能指标分为动态性能指标和稳态性能指标,动态性能指标又可分为随动性能指标和抗扰性能指标。
稳态过程性能稳态误差是系统稳定后实际输出与期望输出之间的差值2. 应用模拟电路来模拟典型二阶系统。
1.2—l 是典型二阶系统原理方块图,其中T0=1秒;T1=0.1秒;K1分别为10;5;2.5;1。
开环传递函数为:)1()1()(11101+=+=S T S K S T S T K S G (2-1)其中,==1T K K 开环增益。
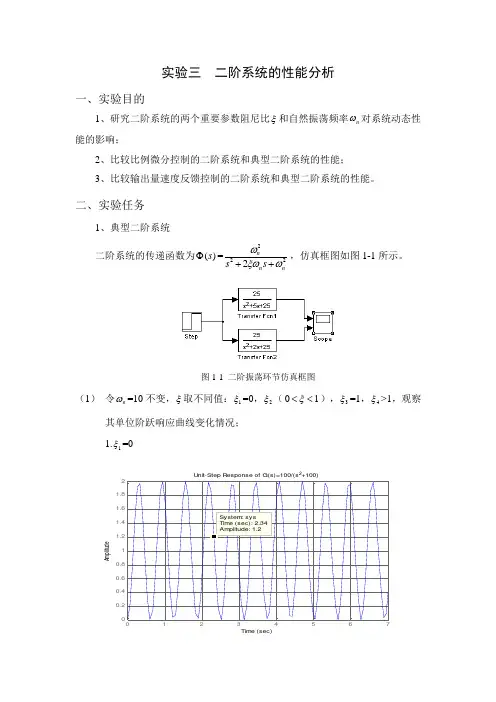
实验三 二阶系统的性能分析一、实验目的1、研究二阶系统的两个重要参数阻尼比ξ和自然振荡频率n ω对系统动态性能的影响;2、比较比例微分控制的二阶系统和典型二阶系统的性能;3、比较输出量速度反馈控制的二阶系统和典型二阶系统的性能。
二、实验任务1、典型二阶系统二阶系统的传递函数为()s Φ=2222nn ns s ωξωω++,仿真框图如图1-1所示。
图1-1 二阶振荡环节仿真框图(1) 令n ω=10不变,ξ取不同值:1ξ=0,2ξ(01ξ<<),3ξ=1,4ξ>1,观察其单位阶跃响应曲线变化情况; 1.1ξ=00.20.40.60.811.21.41.61.82U nit-Step R esponse of G(s)=100/(s 2+100)Tim e (sec)A m p l i t u d e2.2ξ=0.500.20.40.60.81 1.20.20.40.60.811.21.4Unit-Step Response of G(s)=100/(s 2+10s+100)Tim e (sec)A m p l i t u d e3.3ξ=1,00.51 1.50.10.20.30.40.50.60.70.80.91Unit-Step Response of G(s)=100/(s 2+20s+100)Tim e (sec)A m p l i t u d e4.4ξ=50.10.20.30.40.50.60.70.80.91U nit-Step R esponse of G(s)=100/(s 2+100s+100)Tim e (sec)A m p li t u d e(2)令ξ=0不变,n ω取不同值,观察其单位阶跃响应曲线变化情况; 1.n ω=50.20.40.60.811.21.41.61.82U nit-Step R esponse of G(s)=25/(s 2+25)Tim e (sec)A m p li t u d e2.n ω=200.20.40.60.811.21.41.61.82U nit-Step R esponse of G(s)=400/(s 2+400)Tim e (sec)A m p li t u d e(3)令ξ=0.2不变,n ω取不同值,观察其单位阶跃响应曲线变化情况,并计算 超调量%σ和s t ; 1.n ω=501234560.20.40.60.811.21.41.6U nit-Step R esponse of G(s)=25/(s 2+2s+25)Tim e (sec)A m p l i t u d eG=tf([0,0,25],[1,2,25]); C=dcgain(G) [y,t]=step(G); [Y ,k]=max(y);percentovershoot=100*(Y-C)/C i=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1; end setllingtime=t(i) C = 1percentovershoot = 52.6613 setllingtime =3.8810 2.n =100.20.40.60.811.21.41.6U nit-Step R esponse of G(s)=100/(s 2+4s+100)Tim e (sec)A m p l i t u d eG=tf([0,0,100],[1,4,100]); C=dcgain(G) [y,t]=step(G); [Y ,k]=max(y);percentovershoot=100*(Y-C)/C i=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1; end setllingtime=t(i) C = 1percentovershoot =52.6613 setllingtime =1.9405求超调量%σ和s t 的方法:以25425)(2++=Φs s s 为例说明。

二阶系统的性能指标1. 超调量(Overshoot):超调量是指系统实际输出值达到或超过设定值后的最大偏离程度。
超调量大小与系统阻尼比有关,阻尼比越小,超调量越大。
超调量的大小是评价系统抗干扰性的重要指标之一、超调量较小的系统具有更好的稳定性和抗扰性能。
2. 调节时间(Settling Time):调节时间是指系统从初始状态到稳定状态的时间。
也就是系统输出值从设定值到接近设定值所需要的时间。
系统的调节时间越短,说明系统响应快速,性能越好。
3. 稳态误差(Steady-state Error):稳态误差是指系统输出与期望输出之间的差异,它表示系统在稳态下的输出误差大小。
稳态误差大小可以反映系统的静态稳定性能。
稳态误差越小,说明系统的精度越高。
4. 峰值时间(Peak Time):峰值时间是指从初始状态到系统输出值首次达到超调值的时间。
峰值时间越短,说明系统响应速度越快。
峰值时间较短的系统对输入信号的快速变化能够更快地响应,并快速趋于稳定。
除了上述常见指标外,还有一些常用的性能指标包括上升时间(Rise Time),峰值偏差(Peak Overshoot),调节时间百分比(Percent Overshoot)等,这些指标可根据需要进行评价。
上升时间是指系统响应从0%到100%的时间,或者从10%到90%的时间。
上升时间越短,说明系统的响应速度越快。
峰值偏差是指系统在超调过程中达到的最大偏差值。
系统的峰值偏差越小,说明系统对输入信号的超调响应越小。
调节时间百分比是指系统从初始状态到输出值在一定范围内的时间。
调节时间百分比的指标可以根据具体要求进行设置,一般常见的有2%,5%或10%等。
评价二阶系统性能的指标取决于具体的应用和要求,需要根据实际情况进行选择。
对于不同的应用领域,对于性能指标的要求可能会有所不同。
因此,在实际应用中,需要根据系统的具体要求和特点,选择和优化适合的性能指标,以便更好地评估和改进系统的性能。
一、概述在控制系统工程中,频域指标和时域指标是评价系统性能的重要标准。
二阶系统是一类简单且常见的动态系统,其频域指标和时域指标之间存在一定的对应关系。
本文将探讨二阶系统频域指标与动态时域指标之间的对应关系,以及在实际工程中的应用。
二、二阶系统概述1. 二阶系统的数学描述二阶系统是指具有两个传递函数零点和两个传递函数极点的动态系统。
其数学模型可以用如下的传递函数形式表示:$$ G(s) = \frac{K}{s^2 + 2ζω_ns + ω_n^2} $$其中,K为系统的增益,ζ为阻尼比,ω_n为自然频率。
2. 二阶系统的特性二阶系统在频域和时域上有着特定的性能指标,包括频域指标如增益裕度、相位裕度、共振峰值等,以及时域指标如上升时间、峰值时间、定时时间等。
三、频域指标与动态时域指标的对应关系1. 增益裕度与峰值时间的关系在频域分析中,增益裕度是指系统在开环增益相对于临界增益时的增益范围。
而峰值时间是指系统的输出响应中出现的最大过渡过程时间。
二者之间存在如下的关系:$$MG = \frac{1}{\sqrt{1 - ζ^2}}$$$$Tp = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中,MG为增益裕度,Tp为峰值时间。
2. 相位裕度与上升时间的关系相位裕度是指系统在开环相位相对于-180°时的相位范围。
上升时间是指系统输出响应从初始稳态值上升到峰值的时间。
二者之间的关系可以表示为:$$PM = \frac{1}{2ζ\sqrt{1 - ζ^2}}$$$$Tr = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中,PM为相位裕度,Tr为上升时间。
3. 共振峰值与峰值时间的关系共振峰值描述了系统在共振频率处的增益倍数。
而峰值时间则是描述了系统输出响应中的最大过渡过程时间。
二者的关系如下:$$M_p = \frac{1}{2ζ\sqrt{1 - ζ^2}}$$$$Tp = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中,M_p为共振峰值,Tp为峰值时间。
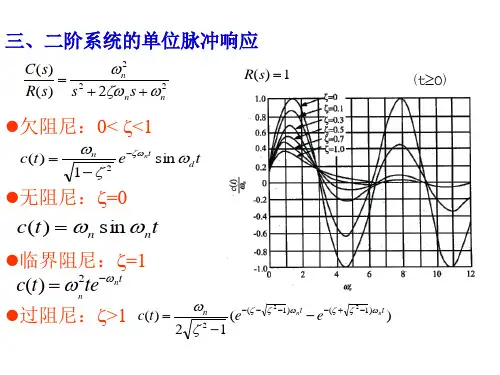
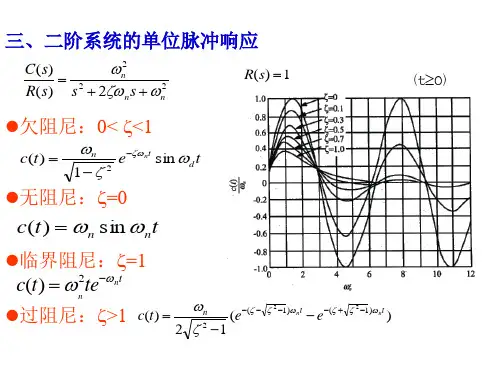
欠阻尼二阶系统动态性能指标计算§3.3.3 欠阻尼二阶系统动态性能指标计算)10(<≤ξ1. 欠阻尼二阶系统极点的两种表示方法(1) 直角坐标表示n n d j j ωξξωωσλ22,11-±-=±=(2)“极”坐标表示⎩⎨⎧=∠=βλωλn⎩⎨⎧-==21sin cos ξβξβ2.欠阻尼二阶系统的单位阶跃响应ss s s R s s C n n n 12)()()(222⋅++=Φ=ωξωω)2()2(]2[2222n n n n n s s s s s s s ωξωξωωξω+++-++= 222)1()(21nn n s s s ωξξωξω-+++-=22222222)1()(11)1()(1nn n n n n s s s s ωξξωωξξξωξξωξω-++-⋅---+++-= 利用复位移定理[])()(a s F e t f L at+=⋅- 系统单位阶跃响应为t e t et h n t n tn n ωξξξωξξωξω2221sin 11cos 1)(-----=--[]t t e n n t n ωξξωξξξξω22221s i n 1c o s 111-+----=-[]t t e nnt n ωξβωξβξξω2221s i n c o s 1c o s s i n 11-⋅+-⋅--=-)10(<≤ξ()t t t hn n ωωcos 190sin1)(-=︒+-=)90,0(︒==βξ)10(<≤ξ系统单位脉冲响应为[]⎥⎦⎤⎢⎣⎡++=Φ='=--222112)()()(n n ns s L s L t h t k ωξωω⎥⎥⎦⎤⎢⎢⎣⎡-++-⋅-=-222221)1()(11n n n ns L ωξξωωξξω欠阻尼二阶系统单位脉冲响应3.欠阻尼二阶系统动态性能指标计算(1)峰值时间p t)()(t k t h ='01sin 122=--=-t en tnn ωξξωξω01sin 2=-t n ωξ,3,2,,012πππωξ=-t n由峰值时间定义(2)超调量00σ()βωξξξω+---=-p n t p t et h pn 221sin 11)(()βπξξξπ+--=--sin 11212e211ξξπ--+=e0σ00100)()()(⨯∞∞-=h h t h p 0011002⨯=--ξξπe超调量0σ与阻尼比ξ之间的关系(3)调节时间 s ts t 对ξ的不连续性调节时间的实际计算方法110.05n n s t t e e -ξω-ξω+-==nns t ξωξωξ5.3)1ln(2105.0ln 2≈-+-= (8.03.0<<ξ))5(0000=∆例1 控制系统结构图如图所示(1)开环增益10=K 时,求系统的动态性能指标;(2)确定使系统阻尼比707.0=ξ的K 值。
二阶系统的性能指标
控制系统的性能指标是评价系统动态品质的定量指标,是定量分析的基础。
系统的时域性能指标通常通过系统的单位阶跃响应进行定义。
常见的性能指标有:上升时间t r 、峰值时间t p 、调整时间t s 、最大超调量M p 、振荡次数N 。
1.评价系统快速性的性能指标
上升时间t r
响应曲线从零时刻出发首次到达
稳态值所需时间。
对无超调系统,
上升时间一般定义为响应曲线从
稳态值的10%上升到90%所需
的时间。
峰值时间t p
响应曲线从零上升到第一个峰值
所需时间。
调整时间t s
响应曲线到达并保持在允许误差
范围(稳态值的±2%或±5%)内所
需的时间。
2.评价系统平稳性的性能指标
✓ 最大超调量M p
响应曲线的最大峰值与稳态值之差。
通常用百分数表示:
%100)()
()(⨯∞∞-≡o o p o p x x t x M 若x o (t p ) < x o (∞),则响应无超调。
✓ 振荡次数N
在调整时间t s 内系统响应曲线的振荡次数。
实测时,可按响应曲线穿越稳态值次数的一半计数。
3.欠阻尼二阶系统的时域性能指标
✓ 上升时间t r
欠阻尼二阶系统的阶跃响应为:0),sin(11)(2≥+--=-t t e t x d t
o n ϕωξξω 根据上升时间的定义有:()1sin 11)(2=+--=-ϕωξξωr d t r o t e t x r
n
2221arccos 11ξωξ
πξωξξπωϕπ--=---=-=n n d r arctg t 显然, ξ一定时,ωn 越大,t r 越小;
ωn 一定时,ξ 越大,t r 越大。
✓ 峰值时间t p 令0)(=dt t dx o ,并将t = t p 代入可得:21ξ
ωπωπ-==n d p t
可见,峰值时间等于阻尼振荡周期T d =2π/ωd 的一半。
且ξ一定,ωn 越大,t p 越小;ωn 一定,ξ 越大,t p 越大。
✓ 最大超调量 M p
%100%100)()
()(21⨯=⨯∞∞-=--ξξπe x x t x M o o p o p
显然,M p 仅与阻尼比ξ有关。
最大超调量直接说明了系统的阻尼特性。
ξ 越大, M p 越小,系统的平稳性越好,当ξ = 0.4~0.8时,可以求得相应的 M p = 25.4%~1.5%。
✓ 调整时间t s
对于欠阻尼二阶系统,其单位阶跃响应的包络线为一对对称于响应稳态分量 1 的指数曲线:211ξξω-±
-t n e n s t ξωξ2
1ln ln --∆-=
当0<ξ<0.7时,
⎪⎪⎩⎪⎪⎨⎧=∆=∆≈--∆-=05.0,302.0,41ln ln 2n
n n s t ξωξωξωξ 当ξ一定时,ωn 越大,t s 越小,系统响应越快。
✓ 振荡次数N
对欠阻尼二阶系统,振荡周期2122ξωπωπ-==n d d T ,则⎪⎪⎩⎪⎪⎨⎧=∆-=∆-==02
.0,1205.0,15.12
2
ξπξξπξd s T t N , N 仅与ξ 有关。
与M p 一样直接说明了系统的阻尼特性。
ξ越大,N 越小,系统平稳性越好。
✓ 结论
▪ 二阶系统的动态性能由ωn 和ξ决定。
▪ 增加ξ可以降低振荡,减小超调量M p 和振荡次数N ,但系统快速性降低,t r 、t p 增加; ▪ ξ一定,ωn 越大,系统响应快速性越好, t r 、 t p 、t s 越小。
▪ 通常根据允许的最大超调量来确定ξ。
ξ一般 选择在0.4~0.8之间,然后再调整ωn 以获得合 适的瞬态响应时间。