控制实验报告二典型系统动态性能和稳定性分析

控制系统的稳定性分析实验总结：控制系统稳定性实验分析提高控制系统稳定性最小相位系统对控制系统的基本要求篇一：实验三、控制系统稳定性分析实验三、控制系统稳定性分析注意：进入实验室前的要求学习教材108-182和402-405页内容；电动机传递函数Gm KT（KT --转矩系数La –电感Ra –电阻）Las?Ra机械系统传递函数d2?d?J2?B?K??T （J—质量B—阻尼K—刚度）dtdt对其求拉斯变换，得到所要传函。

1．试验目的1) 学习并掌握Matlab控制系统的简单使用方法2) 掌握控制系统稳定性分析方法3) 掌握放大环节（如比例调节器）、延迟环节对控制系统稳定性的影响2．验仪器系统安装有matlab软件的计算机实验系统3．实验内容用Bode图分析下面系统中，调节器kc及延迟环节对系统稳定性的影响。

（分析调节器kc时，延迟常数=0; 分析延迟常数时，调节器kc=10）其中Gc(s)为调节器，Gc(s)=k；Gp(s)为功率放大器，Gp(s)=500；Gm(s)为电动机，其电阻r=10欧，电感L=0.1亨，电磁转矩系数Kt =0.01，反电势系数Ke=0.1；H(s)为检测传感器，H(s)=0.1伏/弧度/s；G(s)为被驱动机械对象，可以看成质量-刚度-阻尼系统，J=0.5； -TsK=1；C=0.1; e为系统中的延迟，主要有材料等引起。

(以上参数取值及结构，实验指导老师可是情况变动)4．实验步骤1）写出系统开环传递函数；2）打开matlab 3）建立***.m文件4）编制程序（主要指令: tf、bode、nyquist、margin、pade ; 注释用“%”开头，如: ）5）运行所编制程序6）运行结果记录7）存储所编制程序 6. 结果分析和实验报告K=4; %K=8,12,20,100,200,500,1000 s1=tf([K],[1]); s2=tf([500],[1]); s3=tf([0.01],[0.1,10]);s4=tf([1,0],[0.5,0.1,1]); s5=tf([1],[1,0]); s6=tf([0.1],[1]); s7=tf([0.1],[1]); s8=s3*s4; s9=feedback(s8,0.1,-1); s10=s1*s2*s9*s5*s7 nyquist(s10) bode(s10)K=4时伯德图：Magntude (dB)Phase (deg)Frequency (rad/sec)K=4时传递函数：2 s--------------------------------------0.05 s + 5.01 s + 1.101 s + 10 s实验结果分析：实验程序：T=0.1; %T=0.1,0.8,1,2,4,8,10,11 s1=tf([100],[1]) s2=tf([500],[1]) s3=tf([0.01],[0.1,10]) s4=tf([1,0],[0.5,0.1,1])s5=tf([1],[1,0]) s6=tf([0.1],[1]) s7=tf([0.1],[1]) [num,den]=pade(7 - 4.541e014 s+ 6.054e016 s - 5.881e018 s + 3.97e020 s - 1.676e022 s+ 3.352e023 s-----------------------------------------------------------------------------------0.05 s+ 60.01 s+ 3.521e004 s+ 1.327e007 s+ 3.555e009 s+ 7.07e011 s + 1.061e014 s + 1.196e016 s + 9.877e017 s+ 5.668e019 s + 2.025e021 s + 3.404e022 s + 1.073e022 s实验结果分析：思考题：1. 开环传递函数中的比例对系统稳定性有何影响？答：系统稳定性变得不好。

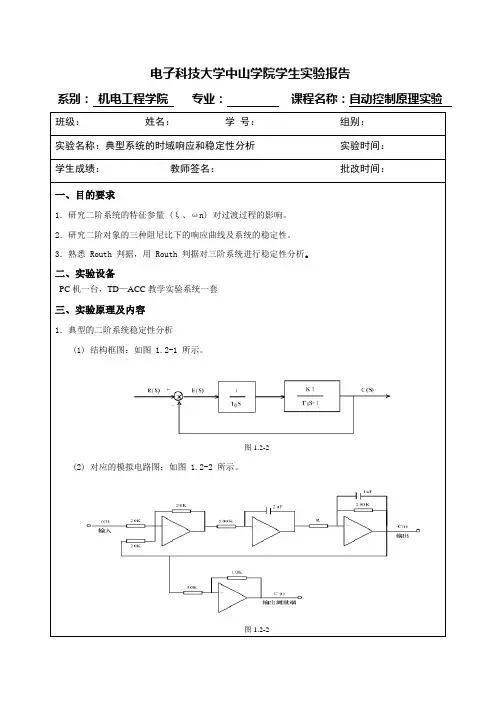
系别：机电工程学院专业：课程名称：自动控制原理实验班级：姓名：学号：组别：实验名称：典型系统的时域响应和稳定性分析实验时间：学生成绩：教师签名：批改时间：一、目的要求1．研究二阶系统的特征参量 (ξ、ωn) 对过渡过程的影响。

2．研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。

3．熟悉 Routh 判据，用 Routh 判据对三阶系统进行稳定性分析。

二、实验设备PC机一台，TD—ACC教学实验系统一套三、实验原理及内容1．典型的二阶系统稳定性分析(1) 结构框图：如图 1.2-1 所示。

图1.2-2(2) 对应的模拟电路图：如图 1.2-2 所示。

图1.2-2系别：机电工程学院专业：课程名称：自动控制原理实验班级：姓名：学号：组别：实验名称：实验时间：学生成绩：教师签名：批改时间：(3) 理论分析系统开环传递函数为：；开环增益：(4) 实验内容先算出临界阻尼、欠阻尼、过阻尼时电阻 R 的理论值，再将理论值应用于模拟电路中，观察二阶系统的动态性能及稳定性，应与理论分析基本吻合。

在此实验中(图 1.2-2)，系统闭环传递函数为：其中自然振荡角频率：2．典型的三阶系统稳定性分析(1) 结构框图：如图 1.2-3 所示。

系别：机电工程学院专业：课程名称：自动控制原理实验班级：姓名：学号：组别：实验名称：实验时间：学生成绩：教师签名：批改时间：图 1.2-3(2)模拟电路图：如图1.2-4 所示。

图 1.2-4(3)理论分析：系统的特征方程为:(4)实验内容：实验前由Routh 判断得Routh 行列式为：系别：机电工程学院专业：课程名称：自动控制原理实验班级：姓名：学号：组别：实验名称：实验时间：学生成绩：教师签名：批改时间：为了保证系统稳定，第一列各值应为正数，所以有五、实验步骤1．将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。

由于每个运放单元均设臵了锁零场效应管，所以运放具有锁零功能。

实验二二阶系统的动态特性与稳定性分析自动控制原理实验报告实验名称：班级：姓名：学号：二阶系统的动态特性与稳定性分析一、实验目的1、掌握二阶系统的电路模拟方法及其动态性能指标的测试技术过阻尼、临界阻尼、欠阻尼状态2、分析二阶系统特征参量（ωn，ξ）对系统动态性能的影响；3、分析系统参数变化对系统稳定性的影响，加深理解“线性系统稳定性至于其结构和参数有关，与外作用无关”的性质；4、了解掌握典型三阶系统的稳定状态、临界稳定、不稳定状态；5、学习二阶控制系统及其阶跃响应的Matlab仿真和simulink实现方法。

二、实验内容1、构成各二阶控制系统模拟电路，计算传递函数，明确各参数物理意义。

2、用Matlab和simulink仿真，分析其阶跃响应动态性能，得出性能指标。

3、搭建典型二阶系统，观测各个参数下的阶跃响应曲线，并记录阶跃响应曲线的超调量σ%、峰值时间tp以及调节时间ts，研究其参数变化对典型二阶系统动态性能和稳定性的影响；4、搭建典型三阶系统，观测各个参数下的阶跃响应曲线，并记录阶跃响应曲线的超调量σ%、峰值时间tp以及调节时间ts，研究其参数变化对典型三阶系统动态性能和稳定性的影响；5、将软件仿真结果与模拟电路观测的结果做比较。

三、实验步骤1、二阶系统的模拟电路实现原理将二阶系统：G(s)=可分解为一个比例环节，一个惯性环节和一个积分环节+2ξsωns+ωn2nG(s)=0236(+s+R1R3R6R2R4R5C1R2R4R5C1C2s)3 2n24512==3+s+s2s+2ξωns+ωnR2R4R5C1C2R6C2(s)=Ui(s)2、研究特征参量ξ对二阶系统性能的影响将二阶系统固有频率ωn=12.5保持不变，测试阻尼系数ξ不同时系统的特性，搭建模拟电路，改变电阻R6可改变ξ的值当R6=50K时，二阶系统阻尼系数ξ=0.8当R6=100K时，二阶系统阻尼系数ξ=0.4当R6=200K时，二阶系统阻尼系数ξ=0.2（1）用Matlab软件仿真实现二阶系统的阶跃响应，计算超调量σ%、峰值时间tp以及调节时间ts。

系统稳定性分析实验报告系统稳定性分析实验报告一、引言系统稳定性是指系统在一定条件下能够保持平衡或者回归到平衡状态的能力。

在工程领域中，系统稳定性是一个重要的指标，它直接影响着系统的可靠性和安全性。

为了更好地理解和评估系统的稳定性，我们进行了一系列的实验，并对实验结果进行了分析。

二、实验目的本次实验的目的是通过对不同系统的稳定性进行分析，探究系统在不同条件下的行为，并深入研究系统的稳定性特征。

通过实验，我们希望能够提供有关系统稳定性的定量指标，并为系统设计和优化提供参考。

三、实验方法1. 实验设备：我们使用了一台实验室提供的系统稳定性测试设备，该设备能够模拟不同条件下的系统行为。

2. 实验步骤：首先，我们选择了多个不同类型的系统进行实验，包括机械系统、电子系统和化学反应系统等。

然后，我们根据实验设备的要求，设置不同的参数和条件，观察系统的稳定性表现，并记录相关数据。

3. 数据分析：我们对实验数据进行了统计和分析，包括系统的响应时间、波动范围、稳定性指标等。

通过对比不同系统和不同条件下的数据，我们得出了一些初步的结论。

四、实验结果与分析1. 不同系统的稳定性表现：根据实验数据，我们发现不同类型的系统在稳定性方面存在一定的差异。

机械系统通常具有较好的稳定性，其响应时间相对较长，波动范围较小；而电子系统的稳定性较差，响应时间较短，波动范围较大。

化学反应系统的稳定性则受到反应物浓度、温度等因素的影响。

2. 系统稳定性指标：我们通过对实验数据的分析，提出了一些系统稳定性的指标，如系统的稳定性系数、稳定性指数等。

这些指标可以用于评估系统的稳定性水平，并为系统设计和优化提供依据。

3. 系统稳定性的影响因素：我们还分析了系统稳定性的影响因素，包括系统结构、参数设置、外界干扰等。

通过对这些因素的研究，我们可以更好地理解系统的稳定性特征，并采取相应的措施提高系统的稳定性。

五、实验结论通过对不同系统的稳定性进行实验和分析，我们得出了以下结论：1. 系统的稳定性与系统类型密切相关，不同类型的系统在稳定性方面表现出不同的特点。

实验二典型系统动态性能和稳定性分析一．实验目的1．学习和掌握动态性能指标的测试方法。

2．研究典型系统参数对系统动态性能和稳定性的影响。

二．实验内容1．观测二阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性能和稳定性的影响。

2．观测三阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性能和稳定性的影响。

三．实验步骤1．熟悉实验装置，利用实验装置上的模拟电路单元，参考本实验附录中的图2.1.1和图2.1.2，设计并连接由一个积分环节和一个惯性环节组成的二阶闭环系统的模拟电路（如用U9、U15、U11和U8连成）。

注意实验接线前必须对运放仔细调零（出厂已调好，无需调节）。

信号输出采用U3单元的O1、信号检测采用U3单元的I1、运放的锁零接U3单元的G1。

2．利用实验设备观测该二阶系统模拟电路的阶跃特性，并测出其超调量和调节时间。

3．改变该二阶系统模拟电路的参数，观测参数对系统动态性能的影响。

4．利用实验装置上的模拟电路单元，参考本实验附录中的图2.2.1和图2.2.2，设计并连接由一个积分环节和两个惯性环节组成的三阶闭环系统的模拟电路（如用U9、U15、U11、U10和U8连成）。

5．利用实验设备观测该三阶系统模拟电路的阶跃特性，并测出其超调量和调节时间。

6．改变该三阶系统模拟电路的参数，观测参数对系统稳定性与动态指标的影响。

7．分析实验结果，完成实验报告。

软件界面上的操作步骤如下：①按通道接线情况:通过上位机界面中“通道选择”选择I1、I2路A/D通道作为被测环节的检测端口,选择D/A通道的O1（“测试信号1”）作为被测对象的信号发生端口.不同的通道,图形显示控件中波形的颜色将不同。

②硬件接线完毕后,检查USB口通讯连线和实验装置电源后，运行上位机软件程序,如果有问题请求指导教师帮助。

③进入实验模式后，先对显示模式进行设置：选择“X-t模式”；选择“T/DIV”为1s/1HZ。

自动控制原理二阶系统动态指标在自动控制原理中，二阶系统的动态特性对整个控制系统的性能至关重要。

以下是对二阶系统动态指标的详细阐述，主要包含稳定性、快速性、准确性、鲁棒性、抗干扰性、调节时间、超调量、阻尼比和频率响应等方面。

一、系统的稳定性稳定性是评估控制系统性能的重要指标。

对于二阶系统，稳定性通常通过观察系统的极点位置来判断。

如果系统的极点位于复平面的左半部分，则系统是稳定的。

此外，系统的稳定性还与阻尼比有关，阻尼比在0到1之间时，系统是稳定的。

二、系统的快速性快速性表示系统响应速度的快慢。

在二阶系统中，快速性通常通过极点的位置来决定。

极点越接近虚轴，系统的响应速度越快。

但需要注意的是，过快的响应速度可能导致系统超调量增大，因此需要综合考虑快速性和稳定性。

三、系统的准确性准确性表示系统输出与期望输出的接近程度。

对于二阶系统，可以通过调整系统的极点和零点位置来提高准确性。

一般来说，增加阻尼比可以提高准确性。

四、系统的鲁棒性鲁棒性表示系统在参数变化或干扰下保持稳定的能力。

对于二阶系统，鲁棒性可以通过调整系统的极点和零点位置来改善。

一般来说，使极点和零点距离越远，系统的鲁棒性越好。

五、系统的抗干扰性抗干扰性表示系统抵抗外部干扰的能力。

对于二阶系统，可以通过增加阻尼比来提高抗干扰性。

阻尼比增大时，系统对外部干扰的抑制能力增强。

六、系统的调节时间调节时间表示系统从受到干扰到恢复稳态所需的时间。

对于二阶系统，调节时间与阻尼比和系统增益有关。

适当增加阻尼比和系统增益可以缩短调节时间。

七、系统的超调量超调量表示系统响应超过稳态值的最大偏差量。

对于二阶系统，超调量与阻尼比有关。

阻尼比越小，超调量越大。

为了减小超调量，可以适当增加阻尼比。

八、系统的阻尼比阻尼比是衡量系统阻尼程度的参数，其值介于0和1之间。

适当的阻尼比可以保证系统具有良好的稳定性和快速性。

对于二阶系统，阻尼比与调节时间和超调量密切相关。

根据实际需求选择合适的阻尼比是关键。

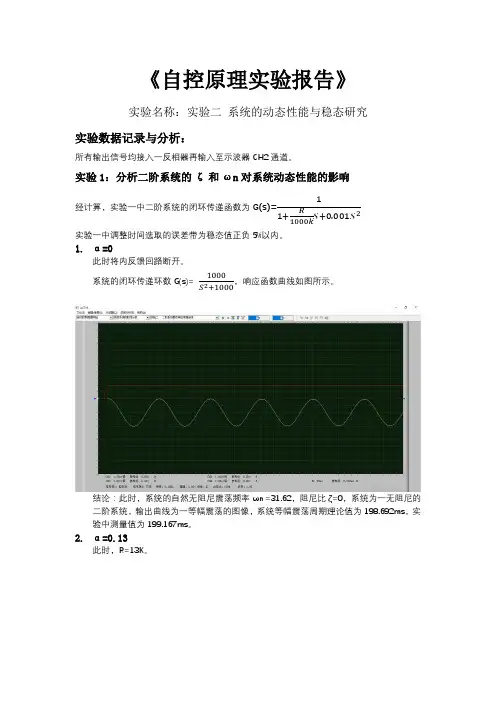
《自控原理实验报告》实验名称：实验二系统的动态性能与稳态研究实验数据记录与分析：所有输出信号均接入一反相器再输入至示波器CH2通道。

实验1：分析二阶系统的ζ和ωn对系统动态性能的影响经计算，实验一中二阶系统的闭环传递函数为G(s)=11+R1000kS+0.001S2实验一中调整时间选取的误差带为稳态值正负5%以内。

1.α=0此时将内反馈回路断开。

系统的闭环传递环数G(s)=1000S2+1000，响应函数曲线如图所示。

结论：此时，系统的自然无阻尼震荡频率ωn =31.62，阻尼比ζ=0，系统为一无阻尼的二阶系统，输出曲线为一等幅震荡的图像，系统等幅震荡周期理论值为198.692ms，实验中测量值为199.167ms。

2.α=0.13此时，R=13K。

系统的闭环传递环数G(s)=1000S2+13S+1000，响应函数曲线如图所示。

结论：此时，系统的自然无阻尼震荡频率ωn =31.62，阻尼比ζ=0.205，系统为一欠阻尼的二阶系统，输出曲线为一震荡后趋于平稳的图像。

理论上系统的输出曲线的超调量σ=51.79%，峰值时间为101.510ms，调节时间为462.812ms。

实验时系统的输出曲线的超调量σ=53.30%，峰值时间为101.667ms，调节时间为433.333ms。

3.α=0.33此时，R=33K。

系统的闭环传递环数G(s)=1000S2+33S+1000，响应函数曲线如图所示。

结论：此时，系统的自然无阻尼震荡频率ωn =31.62，阻尼比ζ=0.521，系统为一欠阻尼的二阶系统，输出曲线为一震荡后趋于平稳的图像。

理论上系统的输出曲线的超调量σ=14.69%，峰值时间为116.400ms，调节时间为182.105ms。

实验时系统的输出曲线的超调量σ=15.74%，峰值时间为115.000ms，调节时间为170.833ms。

4.α=0.44此时，R=44K。

系统的闭环传递环数G(s)=1000S2+44S+1000，响应函数曲线如图所示。

实验二 典型系统动态性能和稳定性分析一．实验目的1．学习和掌握动态性能指标的测试方法。

2．研究典型系统参数对系统动态性能和稳定性的影响。

二．实验内容1．观测二阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性 能和稳定性的影响。

2．观测三阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性 能和稳定性的影响。

三．实验步骤1．熟悉实验装置，利用实验装置上的模拟电路单元，参考本实验附录中的图2.1.1和图 2.1.2 ，设计并连接由一个积分环节和一个惯性环节组成的二阶闭环系统的模拟电路 （如用 U9、 U15、U11和 U8连成）。

注意实验接线前必须对运放仔细调零（出厂已调好， 无需调节）。

信号输出采用 U3单元的 O1、信号检测采用 U3单元的 I1 、运放的锁零接 U3 单元的 G1。

2．利用实验设备观测该二阶系统模拟电路的阶跃特性，并测出其超调量和调节时间。

3．改变该二阶系统模拟电路的参数，观测参数对系统动态性能的影响。

4．利用实验装置上的模拟电路单元，参考本实验附录中的图 2.2.1 和图 2.2.2 ，设计并连接由一个积分环节和两个惯性环节组成的三阶闭环系统的模拟电路（如用 U9、 U15、U11、 U10和 U8 连成）。

5．利用实验设备观测该三阶系统模拟电路的阶跃特性，并测出其超调量和调节时间。

6．改变该三阶系统模拟电路的参数，观测参数对系统稳定性与动态指标的影响。

7．分析实验结果，完成实验报告。

软件界面上的操作步骤如下：① 按通道接线情况 : 通过上位机界面中“通道选择”A/D 通道作为被测环节的检测端口 , 选择 D/A 通道的 O1（“测试信号 1”）作为被测对象的将不同。

② 硬件接线完毕后 , 检查 USB 口通讯连线和实验装置电源后， 运行上位机软件程序 , 如果 有问题请求指导教师帮助。

选择 I1 、 I2 路不同的通道 , 图形显示控件中波形的颜色信号发生端③ 进入实验模式后， 先对显示模式进行设置： 选择 “ X-t 模式”；选择“T/DIV 为 1s/1HZ 。

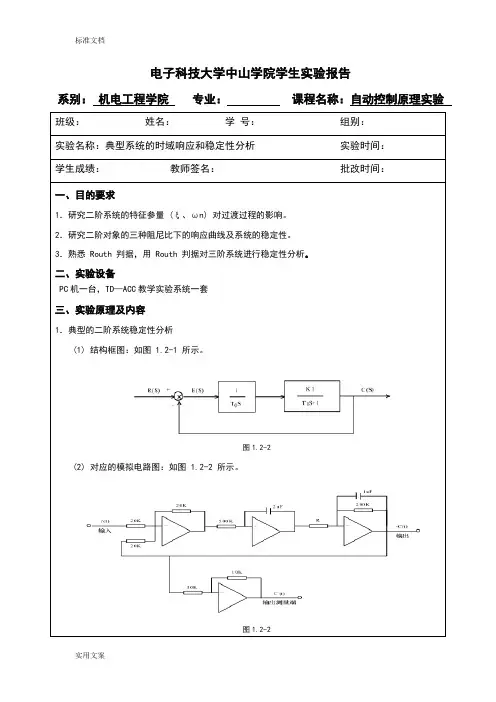
系别：机电工程学院专业：课程名称：自动控制原理实验班级：姓名：学号：组别：实验名称：典型系统的时域响应和稳定性分析实验时间：学生成绩：教师签名：批改时间：一、目的要求1．研究二阶系统的特征参量 (ξ、ωn) 对过渡过程的影响。

2．研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。

3．熟悉 Routh 判据，用 Routh 判据对三阶系统进行稳定性分析。

二、实验设备PC机一台，TD—ACC教学实验系统一套三、实验原理及内容1．典型的二阶系统稳定性分析(1) 结构框图：如图 1.2-1 所示。

图1.2-2(2) 对应的模拟电路图：如图 1.2-2 所示。

图1.2-2系别：机电工程学院专业：课程名称：自动控制原理实验班级：姓名：学号：组别：实验名称：实验时间：学生成绩：教师签名：批改时间：(3) 理论分析系统开环传递函数为：；开环增益：(4) 实验内容先算出临界阻尼、欠阻尼、过阻尼时电阻 R 的理论值，再将理论值应用于模拟电路中，观察二阶系统的动态性能及稳定性，应与理论分析基本吻合。

在此实验中(图 1.2-2)，系统闭环传递函数为：其中自然振荡角频率：2．典型的三阶系统稳定性分析(1) 结构框图：如图 1.2-3 所示。

系别：机电工程学院专业：课程名称：自动控制原理实验班级：姓名：学号：组别：实验名称：实验时间：学生成绩：教师签名：批改时间：图 1.2-3(2)模拟电路图：如图 1.2-4 所示。

图 1.2-4(3)理论分析：系统的特征方程为:(4)实验内容：实验前由 Routh 判断得 Routh 行列式为：系别：机电工程学院专业：课程名称：自动控制原理实验班级：姓名：学号：组别：实验名称：实验时间：学生成绩：教师签名：批改时间：为了保证系统稳定，第一列各值应为正数，所以有五、实验步骤1．将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。

由于每个运放单元均设臵了锁零场效应管，所以运放具有锁零功能。

典型系统动态性能和稳定性分析的电路模拟典型系统动态性能和稳定性分析的电路模拟一、实验目的1、学习和掌握动态性能指标的测试方法。

2、研究典型系统参数对系统动态性能和稳定性的影响。

二、实验内容观测二阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性能和稳定性的影响。

三、实验步骤1、熟悉实验设备，设计并连接一个积分环节和一个惯性环节组成的二阶闭环系统的模拟电路；2、利用实验设备观测二阶系统模拟电路的阶跃特性，并测出其超调量和调节时间；3、改变该二阶系统模拟电路的参数，观测参数对系统动态性能的影响，并记录不同参数下的系统输出曲线。

1.开环传递函数为323()232k W s s s s =+++ den=[1,2,3,2]; roots(den)%开换极点 G=tf(3,[1,2,3,2]);[Gm,Pm,Wcg,Wcp]=margin(G) nyquist(G) bode(G) grid onden=[1,2,3,2]; roots(den)%开换极点ans =-0.5000 + 1.3229i -0.5000 - 1.3229i -1.0000-1.5-1-0.500.51 1.5-1.5-1-0.50.511.5Nyquist DiagramReal AxisI m a g i n a r y A x i sM a g n i t u d e (d B )10-210-110101102P h a s e (d e g )Bode DiagramFrequency (rad/sec)G=tf(3,[1,2,3,2]);[Gm,Pm,Wcg,Wcp]=margin(G)Gm =1.3338Pm =17.1340Wcg =1.7323Wcp =1.5599-3-2-10123-3-2-1123Nyquist DiagramReal AxisI m a g i n a r y A x i s-100-80-60-40-20020M a g n i t u d e (d B)10-210-110101102-270-180-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)G=tf(6,[1,2,3,2]);[Gm,Pm,Wcg,Wcp]=margin(G)Warning: The closed-loop system is unstable. > In lti.margin at 89Gm =0.6669Pm =-16.6613Wcg =1.7323Wcp =1.96822.将系统的开环传函改为323()(232)k W s s s s s =+++den=[1,2,3,2,0]; roots(den)%开换极点ans =-0.5000 + 1.3229i -0.5000 - 1.3229i-1.0000-2.5-2-1.5-1-0.500.5-30-20-10102030Nyquist DiagramReal AxisI m a g i n a r y A x i s-150-100-50050100M a g n i t u d e (d B)1010101010-360-270-180-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)G=tf(3,[1,2,3,2,0]);[Gm,Pm,Wcg,Wcp]=margin(G)Warning: The closed-loop system is unstable.> In lti.margin at 89Gm =0.6667Pm =-43.5555Wcg =1.0000Wcp =1.3325将系统的开环传函改为323()(232)k W s s s s s =+++-4.5-4-3.5-3-2.5-2-1.5-1-0.500.5-60-40-20204060Nyquist DiagramReal AxisI m a g i n a r y A x i s-150-100-50050100M a g n i t u d e (d B)10-210-110101102-360-270-180-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)G=tf(6,[1,2,3,2,0]);[Gm,Pm,Wcg,Wcp]=margin(G)Warning: The closed-loop system is unstable. > In lti.margin at 89Gm =0.3333Pm =-84.3432Wcg =1.0000Wcp =1.6697>> >> 3.2323()(232)k W s s s s s =+++den=[1,2,3,2,0,0]; roots(den)%开换极点ans =0 0-0.5000 + 1.3229i -0.5000 - 1.3229i -1.0000-600-500-400-300-200-1000100-50-40-30-20-1001020304050Nyquist DiagramReal AxisI m a g i n a r y A x i sM a g n i t u d e (d B )10-210-1100101102P h a s e (d e g )Bode DiagramFrequency (rad/sec)G=tf(3,[1,2,3,2,0,0]);[Gm,Pm,Wcg,Wcp]=margin(G)Warning: The closed-loop system is unstable.> In lti.margin at 89Gm =InfPm =-115.6441Wcg =NaNWcp =-1200-1000-800-600-400-2000200-100-80-60-40-20020406080100Nyquist DiagramReal AxisI m a g i n a r y A x i sM a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/sec)G=tf(6,[1,2,3,2,0,0]);[Gm,Pm,Wcg,Wcp]=margin(G)Warning: The closed-loop system is unstable.> In lti.margin at 89 Gm =InfPm =-154.5325Wcg =NaNWcp =1.4900>>RFFNVUUH。