复摆运动状态的研究

单复摆运动特性研究实验报告摘要：单复摆运动是一种重要的力学运动，本实验通过研究单摆和复摆的运动特性，深入了解其运动规律。

通过实验测量单摆和复摆的周期和振幅，分析了参数对于振动特性的影响。

实验结果表明，单摆和复摆的周期与摆长有关，而与摆球质量无关；振幅与摆球质量成正比，与摆长无关。

这些结果对于进一步了解单复摆运动以及相关物理现象具有一定的参考价值。

关键词：单摆；复摆；周期；振幅一、引言单摆和复摆是一种重要的力学运动，在物理学的研究中具有重要的应用价值。

单摆是指一个质点固定在一根轻质不可伸长的细线上，沿着垂直方向做简谐振动。

复摆是指两个或两个以上的质点通过不可伸长的轻绳相连，在重力作用下做振动。

研究单摆和复摆的运动特性，可以进一步对力学定律进行验证和应用。

二、实验目的1.研究单摆和复摆的周期与摆长的关系；2.分析振幅对单摆和复摆的影响；3.探究单摆和复摆的运动规律。

三、实验原理1.单摆运动特性单摆运动特性由摆长l和重力加速度g决定。

根据单摆的运动方程，可以推导出单摆的周期与摆长的关系公式为：T=2π√(l/g)2.复摆运动特性复摆运动特性由摆长l、重力加速度g和摆球质量m决定。

根据复摆的运动方程，可以推导出复摆的周期与摆长和摆球质量的关系公式为：T=2π√(l/[(g+g')/m])其中，g'为轻球受到的有效重力加速度。

四、实验装置与测量方法实验装置包括摆线、摆球、计时器等。

实验步骤如下：1.调整单摆的摆长，测量并记录单摆的周期和振幅；2.调整复摆的摆长和摆球质量，测量并记录复摆的周期和振幅。

五、实验结果与分析通过实验测量，得到了单摆和复摆的周期和振幅的数据。

根据实验数据，计算出了周期与摆长、振幅与摆球质量的相关系数，并绘制出相应的曲线。

通过分析实验结果1.单摆的周期与摆长成正比，与摆球质量无关；2.复摆的周期与摆长成正比，与摆球质量成反比；3.振幅与摆球质量成正比，与摆长无关。

六、实验结论单摆和复摆的周期与摆长有关，而与摆球质量的关系不同。

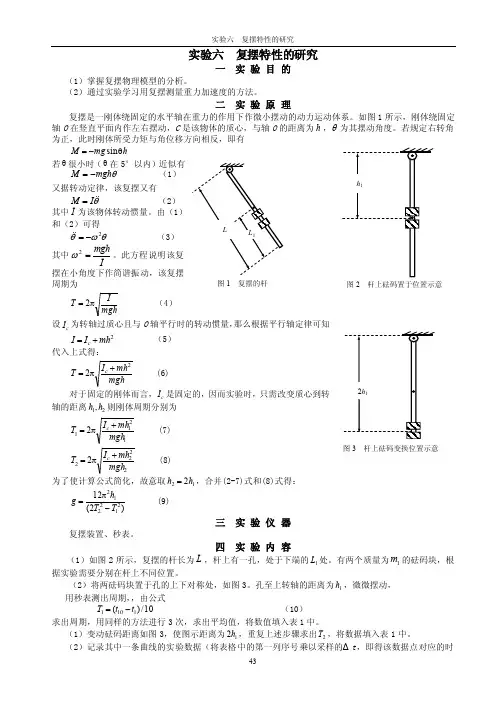
实验六 复摆特性的研究一 实 验 目 的（1）掌握复摆物理模型的分析。

（2）通过实验学习用复摆测量重力加速度的方法。

二 实 验 原 理复摆是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系。

如图1所示，刚体绕固定轴O 在竖直平面内作左右摆动，C 是该物体的质心，与轴O 的距离为h ，θ为其摆动角度。

若规定右转角为正，此时刚体所受力矩与角位移方向相反，即有h mg M θ-=sin 若θ很小时（θ在5°以内）近似有θmgh M -= （1） 又据转动定律，该复摆又有θ I M = （2） 其中I 为该物体转动惯量。

由（1）和（2）可得θωθ2-= （3） 其中Imgh=2ω。

此方程说明该复摆在小角度下作简谐振动，该复摆周期为mghIT π=2 （4） 设c I 为转轴过质心且与O 轴平行时的转动惯量，那么根据平行轴定律可知2mh I I c += （5） 代入上式得：mghmh I T c 22+π= (6) 对于固定的刚体而言，c I 是固定的，因而实验时，只需改变质心到转轴的距离21,h h 则刚体周期分别为12112mgh mh I T c +π= (7) 22222mgh mh I T c +π= (8)为了使计算公式简化，故意取122h h =，合并(2-7)式和(8)式得：)2(12212212T T h g -π= (9) 三 实 验 仪 器复摆装置、秒表。

四 实 验 内 容（1）如图2所示，复摆的杆长为L ，杆上有一孔，处于下端的1L 处。

有两个质量为1m 的砝码块，根据实验需要分别在杆上不同位置。

（2）将两砝码块置于孔的上下对称处，如图3。

孔至上转轴的距离为1h ，微微摆动，用秒表测出周期，，由公式10/)(1101t t T -= （10）求出周期，用同样的方法进行3次，求出平均值，将数值填入表1中。

（1）变动砝码距离如图3，使图示距离为12h ，重复上述步骤求出2T ，将数据填入表1中。

复摆振动的研究
实验目的：1、考查复摆振动时振动周期与质心到支点距离的关系； 2、测出重力加速度、回转半径和转动惯量。

实验仪器：
实验原理：一个围绕定轴转动的刚体就是复摆，刚体绕固定轴O 在竖直平面内作左右摆动，C 是该物体的质心，与轴O 的距离为 h ,θ 为其摆动角度。

如图 1 所示
当摆的振幅甚小时，其震动周期 T 为
（1）
设 I G 为转轴过质心且与O 轴平行时的转动惯量，那么根据平行轴定律可知
（2）
而 I G 又可以写成为 I G =mk 2， k 就是复摆对 G 轴的回转半径，由此可将式（1）改为
（3）
实验内容：1、重心G 的位置S G = (h=│S -S G │)
的重心端作为正端，选择复摆上以下刻度位置作为支点位
4、用物理天平测量复摆的质量m. m=
数据处理与分析：（h=│S-S
│）
G
S xx=∑x i2-(∑x i)2/n=
S yy =∑y i 2-(∑y i )2/n = S xy =∑x i y i -∑x i ∑y i /n=
=
∙==-===∑∑yy xx xy i i xx
xy S S S r
n x b n y a
S S b ˆˆˆ
r b n r S b ⋅⎪⎪⎭
⎫ ⎝
⎛--=2
12= b g ⋅=24π =
b s g g U b
=)(=
b
s g g g U g
g U b =)
(=)(=
实验结果与评价：
实验感想：。

复摆的实验报告-精品复摆的实验报告-精品2020-12-12【关键字】方案、目录、情况、方法、动力、成绩、质量、系统、有效、平衡、了解、研究、特点、位置、关键、理想、项目、资源、作用、水平、任务、反映、速度、关系、分析、调节、指导、分工、方向、中心篇一：实验报告_复摆实验【实验题目】复摆实验【实验记录】1. 复摆中心G的位置：0刻度处3. 计算重力加速度g:4?2T12?T22T12?T22g2(h1?h2)2(h1?h2)g=9.905kg/m214. 作T-h图5. 利用mgT2h?4?2IG?4?2mh2，作T2h~h2关系图，考察其线形关系，由最小二乘法计算g和复摆对重心的转动惯量IG。

IG=0.002536kg*m*m【结论与讨论】误差分析：1 在实验中，复摆的摆动不能很好的控制在同一平面摆动。

2 实验前没有很好的调节复摆对称。

3 复摆摆动可能幅度过大。

结论：利用复摆可以测量重力加速度，同时还可以由这个方法衍生开来测量不规则物体的转动惯量。

成绩（满分30分）：指导教师签名：日期：篇二：复摆实验报告【实验题目】复摆实验【实验记录】1. 复摆中心g的位置：0刻度处3. 计算重力加速度g:4?2t12?t22t12?t22g2(h1?h2)2(h1?h2)g=9.905kg/m2 14. 作t-h图5. 利用mgt2h?4?2ig?4?2mh2，作t2h~h2关系图，考察其线形关系，由最小二乘法计算g和复摆对重心的转动惯量ig。

ig=0.002536kg*m*m 【结论与讨论】误差分析：1 在实验中，复摆的摆动不能很好的控制在同一平面摆动。

2 实验前没有很好的调节复摆对称。

3 复摆摆动可能幅度过大。

结论：利用复摆可以测量重力加速度，同时还可以由这个方法衍生开来测量不规则物体的转动惯量。

成绩（满分30分）：指导教师签名：日期：2篇二：实验报告_复摆实验【实验题目】复摆实验【实验记录】1. 复摆中心g的位置：3. 计算重力加速度g:4?2t12?t22t12?t22= g2(h1?h2)2(h1?h2)g= 14. 作t-h图5. 利用mgth?4?ig?4?mh，作th~h关系图，考察其线形关系，由最小二乘法计 22222算g和复摆对重心的转动惯量ig。

复摆实验报告复摆实验报告摆动是物体在受到外力作用下围绕某一固定点旋转的运动形式。

而复摆实验是一种通过摆动的方式来研究物体的运动规律的实验。

本次实验我们使用了复摆装置，通过观察和记录复摆的运动情况，探究摆动的特性和规律。

实验目的本次实验的目的是研究复摆的运动规律，包括摆动周期与摆长、质量等因素之间的关系，以及摆动的频率与角度的关系。

通过实验数据的收集和分析，我们可以得出一些定量的结论，进一步认识和理解复摆的运动特性。

实验装置本次实验使用的复摆装置包括一个支架、两个摆球和一个可调节的摆长装置。

摆球通过细线与支架相连，可以在一定范围内调整摆长。

实验中，我们使用了不同质量的摆球，以便观察质量对摆动的影响。

实验步骤1. 将支架固定在实验台上，并调整好摆长装置的位置。

2. 将摆球分别挂在细线上，并通过细线固定在支架上。

3. 调整摆球的位置和摆长，使其能够自由摆动。

4. 用计时器记录摆球的摆动周期，并重复多次实验以获得准确的数据。

5. 改变摆球的质量，重复步骤4，以观察质量对摆动周期的影响。

6. 改变摆球的摆长，重复步骤4，以观察摆长对摆动周期的影响。

实验结果与分析通过实验数据的收集和分析，我们得到了以下结果：1. 摆动周期与摆长的关系：在实验中，我们发现摆长对摆动周期有着明显的影响。

当摆长增加时，摆动周期也随之增加。

这是因为较长的摆长使得摆球的运动路径更长，需要更多的时间来完成一个完整的摆动。

2. 摆动周期与质量的关系：实验结果还表明，质量对摆动周期也有一定的影响。

当质量增加时，摆动周期减小。

这是因为较大的质量使得摆球的惯性增加，从而减小了受到重力的影响，使得摆动更快。

3. 摆动频率与角度的关系：在实验中，我们还观察到摆动频率与摆动角度之间存在着一定的关系。

当摆动角度较小时，摆动频率较大；而当摆动角度较大时，摆动频率较小。

这是因为较大的摆动角度使得摆球的速度较快，需要更多的时间来完成一个完整的摆动，从而降低了摆动频率。

复摆的实验报告.doc摘要：本实验通过利用复摆的摆动周期和摆长与摆角度之间的关系，通过多次实验来研究复摆的动力学规律和特性。

实验结果表明，复摆的摆动周期受到重力加速度和摆长的影响，摆长越长，摆臂相对较长，振幅相对小，周期越长。

同时，复摆的摆角度对振幅和周期都产生了影响，当摆角度较小时，振幅较小，周期较长。

关键词：复摆，摆动周期，摆角度，摆长Abstract:In this experiment, the dynamic laws and characteristics of the compound pendulum are studied by utilizing the relationship between the swinging period and the swinging length and swing angle of the compound pendulum. The experimental results show that the swinging period of the compound pendulum is affected by the gravity acceleration and the swinging length. The longer the swinging length, the longer the swinging arm, the smaller the amplitude, andthe longer the period. At the same time, the swinging angle of the compound pendulum affects the amplitude and period. When the swinging angle is small,the amplitude is small and the period is long.Keywords: compound pendulum, swinging period, swinging angle, swinging length实验方案：所用仪器：复摆、计时器、卡尺、直尺、秤。

复摆实验报告摆实验是物理学中经典而又重要的实验之一，通过对摆的运动规律的观察和研究，可以更好地理解运动的基本原理和规律。

在本次实验中，我们将使用简单摆进行观察和测量，并对实验结果进行分析和讨论。

实验目的：1. 通过实验观察和测量，研究简单摆的运动规律。

2. 利用实验结果分析物理规律，加深对摆运动的理解。

实验器材：1. 长线2. 钢球3. 支架4. 计时器5. 测量尺6. 重物实验步骤：1. 将支架固定在实验台上，并用线将钢球系于支架上方。

2. 保证摆线长度合适，并进行调整以使钢球在与支架正下方位置静止。

3. 调整摆球的起始位置，使其离开平衡位置。

4. 利用计时器，记录摆球从起始位置经过相同位置所用的时间，进行多次测量。

5. 根据测量结果，计算摆球的周期和频率。

6. 在实验过程中，可改变摆线长度、摆球质量或起始位置等条件，分析对摆球运动的影响。

实验结果：通过多次实验记录和测量，我们得出以下实验结果：1. 摆球的周期与摆长无关。

我们在实验中改变了摆线的长度，但发现摆球的周期并没有受到明显影响，仍保持稳定。

2. 摆球的周期与摆球质量有关。

在实验中，我们改变了摆球的质量，发现摆球的周期与质量呈正相关关系，即质量越大，周期越长。

3. 摆球的频率与周期呈倒数关系。

我们通过计算发现，摆球的频率与周期呈倒数关系，即频率等于1除以周期。

4. 摆球的起始位置影响摆动幅度。

我们改变了摆球的起始位置，发现起始位置越高，摆动幅度越大，起始位置越低，摆动幅度越小。

实验分析：通过对上述实验结果的观察和分析，我们可以得出以下结论：1. 简单摆的运动规律是周期性的，不受摆线长度的影响。

这是因为摆线长度只影响摆球的运动速度，而不影响其运动周期。

2. 摆球的周期与摆球质量正相关。

这是因为质量越大的摆球，受到的重力作用越大，需要更长的时间才能完成一次完整的振动。

3. 摆球的频率与周期呈倒数关系。

频率的大小表示单位时间内的振动次数，而周期则表示完成一次振动所需的时间，因此两者呈倒数关系。

复摆的周期与相位关系研究复摆是一种简单而又经典的物理现象，它在物理学的教学中扮演着重要的角色。

复摆的周期与相位关系一直是研究的热点之一。

本文将从周期和相位两个方面探讨复摆的特性。

周期是描述复摆运动的重要参数之一。

周期指的是复摆从一个极点（例如最大振幅位置）回到同一位置所需的时间。

周期与复摆的长度、重力加速度以及摆动角度有关。

根据简谐振动的理论，周期与摆长成反比，与重力加速度和摆动角度的正弦函数成正比。

因此，可以通过改变摆长、重力加速度或摆动角度来改变复摆的周期。

相位是描述复摆运动状态的重要指标。

相位指的是复摆在某一时刻与标准位置（通常为平衡位置）的偏离程度。

相位与时间的关系可以用相位角来表示。

相位角是一个角度，它描述了复摆在某一时刻相对于标准位置的偏移角度。

相位角的变化与时间的关系可以通过正弦函数来描述。

根据简谐振动的理论，相位角随时间的变化满足正弦函数的规律。

因此，可以通过观察相位角随时间的变化来研究复摆的相位特性。

研究表明，复摆的周期与摆长之间存在着密切的关系。

当摆长增加时，周期也会相应地增加。

这是因为摆长的增加会使复摆的振幅增大，从而增加复摆的运动时间。

此外，重力加速度的变化也会影响复摆的周期。

在地球上，重力加速度的值约为9.8米/秒²。

如果在其他行星或卫星上进行复摆实验，由于重力加速度的不同，复摆的周期也会有所变化。

复摆的相位特性也非常有趣。

在复摆的运动过程中，相位角随时间的变化呈现出周期性的规律。

当复摆从一个极点回到同一位置时，相位角也会回到初始值。

这种周期性的变化使得复摆的相位角可以用来描述复摆的运动状态。

此外，复摆的相位角还可以用来计算复摆的速度和加速度等运动参数。

在实际应用中，复摆的周期与相位关系研究对于测量时间、频率和振动等方面具有重要意义。

例如，在钟表制造中，可以利用复摆的周期性来测量时间。

通过调整复摆的摆长和重力加速度，可以实现钟表的精确计时。

此外，在天文学中，可以利用复摆的周期性来测量星体的运动速度和轨道参数。