深圳中考专项练习-胡不归和阿氏圆教案

2020年中考复习专题：“胡不归”问题在前面的最值问题中往往都是求某个线段最值或者形如PA+PB最值，除此之外我们还可能会遇上形如“PA+kPB”这样的式子的最值，此类式子一般可以分为两类问题：(1)胡不归问题；(2)阿氏圆.本文简单介绍“胡不归”模型【故事介绍】从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家，根据“两点之间线段最短”，虽然从他此刻位置A到家B之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭.邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归?胡不归?”(“胡”同“何”)而如果先沿着驿道AC先走一段，再走砂石地，会不会更早到家?【模型建立】如图，一动点P在直线MN外的运动速度为V1，在直线MN上运动的速度为V2，且V1＜V2，A、B为定点，点C在直线MN上，确定点C的位置使ACV2+BCV1的值最小【问题分析】AC V2+BCV1=1V1(BC+V1V2AC)，记k=V1V2，即求BC+kAC的最小值【问题解决】构造射线AD使得sin∠DAN＝k，CHAC=k，CH＝kAC.将问题转化为求BC+CH最小值，过B点作BH⊥AD交MN于点C，交AD于H点，此时BC+CH 取到最小值，即BC+kAC最小.【模型总结】在求形如“PA+kPB＂的式子的最值问题中，关键是构造与kPB相等的线段，将“PH+kPB”型问题转化为“PA+PC”型.而这里的PB必须是一条方向不变的线段，方能构造定角利用三角函数得到kPB的等线段.【2019长沙中考】如图，△ABC中，AB＝AC＝10，tanA=2，BE⊥AC于点E，D是线段BEBD的最小值是上的一个动点，则CD+√55【2019南通中考】如图，平行四边形ABCD中，∠DAB=60°，AB＝6，BC=2，P为边CD上PD的最小值等于的一动点，则PB+√32【2014成都中考】如图，已知抛物线y＝k8(x+2)(x-4)(k为常数，且k>0)与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y＝−√33x+b与抛物线的另一交点为D.(1)若点D的横坐标为-5，求抛物线的函数表达式(2)在(1)的条件下，设F为线段BD上一点(不含端点)，连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止，当点F的坐标是多少时，点M在整个运动过程中用时最少?【2018重庆中考】抛物线y=−√66x2−2√33x+√6与x轴交于点A，B(点A在点B的左边)，与y轴交于点C.点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC交于点E;将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当PE+12EC的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标。

（一）最短路径--------点P 在直线上运动------“胡不归”问题（PA+k·PB 型）如图1-1-1所示，已知sin∠MBN=k,点P 为角∠MBN 其中一边BM 上的一个动点，点A 在射线BM、BN 的同侧，连接AP,则当“PA+k·PB”的值最小时，P 点的位置如何确定?分析：本题的关键在于如何确定“k·PB”的大小，过点P 作PQ⊥BN 垂足为Q，则k·PB=PB·sin∠MBN=PQ,∴本题求“PA+k·PB”的最小值转化为求“PA+PQ”的最小值(如图1-1-2)，即A、P、Q 三点共线时最小（如图1-1-3），本题得解。

“胡不归”一般解题步骤：构造新的线段，使其等于k ·PB.Ps ：一般系数k 满足0＜k ＜1时直接构造，若k ＞1时，需要先提取系数，如”PA+2PB=2(21PA+PB).【例题精讲】1.如图，四边形ABCD 是菱形，AB=4，且∠ABC=60°，M 为对角线BD（不含B 点）上任意一点,则AM+21BM 的最小值为___________.2.图1,抛物线与x 轴交于A(−1,0),B(3,0),顶点为D(1,−4)，点P 为y 轴上一动点。

(1)求抛物线的解析式；(2)在BC 下方的抛物线上，是否存在异于点D 的点E ，使S 三角形BCE=S 三角形BCD ？若存在，求出E 的坐标；(3)如图2,点M(−32,m)在抛物线上,求MP+22PC 的最小值。

3.如图,抛物线y=1/2x2+mx+n 与直线y=−1/2x+3交于A,B 两点,交x 轴于D,C 两点,连接AC,BC,已知A(0,3),C(3,0).(Ⅰ)求抛物线的解析式和tan ∠BAC 的值；(Ⅱ)在(Ⅰ)条件下：(1)P 为y 轴右侧抛物线上一动点，连接PA ，过点P 作PQ ⊥PA 交y 轴于点Q ，问：是否存在点P 使得以A ，P ，Q 为顶点的三角形与△ACB 相似?若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由。

阿氏圆专题在前面的“胡不归”问题中，我们见识了“kPA+PB”最值问题，其中P 点轨迹是直线，而当P 点轨迹变为圆时，即通常我们所说的“阿氏圆”问题．【模型来源】“阿氏圆”又称为“阿波罗尼斯圆”，如下图，已知A 、B 两点，点P 满足PA ：PB=k （k≠1），则满足条件的所有的点P 的轨迹构成的图形为圆．这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”.【模型建立】如图 1 所示，⊙O 的半径为R ，点 A 、B 都在⊙O 外 ，P 为⊙O 上一动点，已知R=25OB ，连接 PA 、PB ，则当“PA+25PB ”的值最小时，P 点的位置如何确定？解决办法：如图2，在线段 OB 上截取OC 使 OC=25R ，则可说明△BPO 与△PCO 相似，则有25PB=PC 。

故本题求“PA+25PB ”的最小值可以转化为“PA+PC ”的最小值，其中与A 与C 为定点，P 为动点，故当 A 、P 、C 三点共线时，“PA+PC ”值最小。

【技巧总结】计算PA k PB +的最小值时，利用两边成比例且夹角相等构造母子型相似三角形问题：在圆上找一点P 使得PA k PB +的值最小，解决步骤具体如下： 1. 如图，将系数不为1的线段两端点与圆心相连即OP ，OB2. 计算出这两条线段的长度比OPk OB = 3. 在OB 上取一点C ，使得OC k OP =，即构造△POM△△BOP ，则PCk PB=，PC k PB =4. 则=PA k PB PA PC AC ++≥，当A 、P 、C 三点共线时可得最小值典题探究 启迪思维 探究重点例题1. 如图，在Rt △ABC 中，∠C=90°，AC=4，BC=3，以点C 为圆心，2为半径作圆C ，分别交AC 、BC于D 、E 两点，点P 是圆C 上一个动点，则12PA PB +的最小值为__________．【分析】这个问题最大的难点在于转化12PA ，此处P 点轨迹是圆，注意到圆C 半径为2，CA=4，连接CP ，构造包含线段AP 的△CPA ，在CA 边上取点M 使得CM=2，连接PM ，可得△CPA ∽△CMP ，故PA ：PM=2:1，即PM=12PA ．问题转化为PM+PB ≥BM 最小值，故当B ，P ，M 三点共线时得最小值，直接连BM变式练习>>>1．如图1，在RT △ABC 中，∠ACB=90°，CB=4，CA=6，圆C 的半径为2，点P 为圆上一动点，连接AP ,BP ， 求①BP AP 21+，②BP AP +2，③BP AP +31，④BP AP 3+的最小值.[答案]：①=37，②=237，③=3372，④= EABC DP例题2. 如图，点C 坐标为(2,5)，点A 的坐标为(7,0)，△C 的半径为10,点B 在△C 上一动点，AB OB 55的最小值为________.[答案]：5. 变式练习>>>2．如图，在平面直角坐标系xoy 中，A(6,-1)，M(4,4)，以M 为圆心，22为半径画圆，O 为原点，P 是⊙M 上一动点，则PO+2PA 的最小值为________.[答案]：10.例题3. 如图，半圆的半径为1，AB为直径，AC、BD为切线，AC＝1，BD＝2，P为上一动点，求PC+PD的最小值．【解答】解：如图当A、P、D共线时，PC+PD最小．理由：连接PB、CO，AD与CO交于点M，△AB＝BD＝4，BD是切线，△△ABD＝90°，△BAD＝△D＝45°，△AB是直径，△△APB＝90°，△△P AB＝△PBA＝45°，△P A＝PB，PO△AB，△AC＝PO＝2，AC△PO，△四边形AOPC是平行四边形，△OA＝OP，△AOP＝90°，△四边形AOPC是正方形，△PM＝PC，△PC+PD＝PM+PD＝DM，△DM△CO，△此时PC+DP最小＝AD﹣AM＝2﹣＝．变式练习>>>3．如图，四边形ABCD为边长为4的正方形，△B的半径为2，P是△B上一动点，则PD+PC的最小值为5；PD+4PC的最小值为10．【解答】解：△如图，连接PB、在BC上取一点E，使得BE＝1．△PB2＝4，BE•BC＝4，△PB2＝BE•BC，△＝，△△PBE＝△CBE，△△PBE△△CBE，△＝＝，△PD+PC＝PD+PE，△PE+PD≤DE，在Rt△DCE中，DE＝＝5，△PD+PC的最小值为5．△连接DB ，PB ，在BD 上取一点E ，使得BE ＝，连接EC ，作EF △BC 于F ．△PB 2＝4，BE •BD ＝×4＝4，△BP 2＝BE •BD ，△＝，△△PBE ＝△PBD ，△△PBE △△DBP ， △＝＝，△PE ＝PD ，△PD +4PC ＝4（PD +PC ）＝4（PE +PC ），△PE +PC ≥EC ，在Rt△EFC 中，EF ＝，FC ＝，△EC ＝，△PD +4PC 的最小值为10．故答案为5，10．例题4. 如图，已知正方ABCD 的边长为6，圆B 的半径为3，点P 是圆B 上的一个动点，则12PD PC 的最大值为_______．【分析】当P 点运动到BC 边上时，此时PC=3，根据题意要求构造12PC ，在BC 上取M 使得此时PM=32，则在点P 运动的任意时刻，均有PM=12PC ，从而将问题转化为求PD-PM 的最大值．连接PD ，对于△PDM ，PD-PM ＜DM ，故当D 、M 、P 共线时，PD-PM=DM 为最大值152．AB CDPABCDP MMPDCBAABCDPMMPDCBA变式练习>>>4．（1）如图1，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．（2）如图2，已知菱形ABCD的边长为4，△B＝60°，圆B的半径为2，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．图1 图2【解答】解：（1）如图3中，在BC上取一点G，使得BG＝4．△＝＝，＝＝，△＝，△△PBG＝△PBC，△△PBG△△CBP，△＝＝，△PG＝PC，△PD+PC＝DP+PG，△DP+PG≥DG，△当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝．△PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大，最大值为DG＝．故答案为，（2）如图4中，在BC上取一点G，使得BG＝1，作DF△BC于F．△＝＝2，＝＝2，△＝，△△PBG＝△PBC，△△PBG△△CBP，△＝＝，△PG＝PC，△PD+PC＝DP+PG，△DP+PG≥DG，△当D、G、P共线时，PD+PC的值最小，最小值为DG，在Rt△CDF中，△DCF＝60°，CD＝4，△DF＝CD•sin60°＝2，CF＝2，在Rt△GDF中，DG＝＝△PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝．故答案为，．例题5. 如图，抛物线y=﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y=﹣12x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．（1）求抛物线y=﹣x2+bx+c的表达式；（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求AM+CM它的最小值．【解答】解：（1）∵点A（﹣4，﹣4），B（0，4）在抛物线y=﹣x2+bx+c上，∴，∴，∴抛物线的解析式为y=﹣x2﹣2x+4；（2）设直线AB的解析式为y=kx+n过点A，B，∴，∴，∴直线AB的解析式为y=2x+4，设E（m，2m+4），∴G（m，﹣m2﹣2m+4），∵四边形GEOB是平行四边形，∴EG=OB=4，∴﹣m2﹣2m+4﹣2m﹣4=4，∴m=﹣2，∴G（﹣2，4）；（3）①如图1，由（2）知，直线AB的解析式为y=2x+4，∴设E（a，2a+4），∵直线AC：y=﹣x﹣6，∴F（a，﹣a﹣6），设H（0，p），∵以点A，E，F，H为顶点的四边形是矩形，∵直线AB的解析式为y=2x+4，直线AC：y=﹣x﹣6，∴AB⊥AC，∴EF为对角线，∴（﹣4+0）=（a+a），（﹣4+p）=（2a+4﹣a﹣6），∴a=﹣2，P=﹣1，∴E（﹣2，0）．H（0，﹣1）；②如图2，由①知，E（﹣2，0），H（0，﹣1），A（﹣4，﹣4），∴EH=，AE=2，设AE交⊙E于G，取EG的中点P，∴PE=，连接PC交⊙E于M，连接EM，∴EM=EH=，∴=，∵=，∴=，∵∠PEM=∠MEA，∴△PEM∽△MEA，∴=，∴PM=AM，∴AM+CM的最小值=PC，设点P（p，2p+4），∵E（﹣2，0），∴PE2=（p+2）2+（2p+4）2=5（p+2）2，∵PE=，∴5（p+2）2=，∴p=或p=﹣（由于E（﹣2，0），所以舍去），∴P（，﹣1），∵C（0，﹣6），∴PC==，即：AM+CM=．变式练习>>>5．如图1，抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM△AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若＝，求m的值；（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E′A+E′B的最小值．【解答】解：（1）令y ＝0，则ax 2+（a +3）x +3＝0， △（x +1）（ax +3）＝0，△x ＝﹣1或﹣，△抛物线y ＝ax 2+（a +3）x +3（a ≠0）与x 轴交于点A （4，0）， △﹣＝4，△a ＝﹣．△A （4，0），B （0，3）， 设直线AB 解析式为y ＝kx +b ，则，解得，△直线AB 解析式为y ＝﹣x +3．（2）如图1中，△PM △AB ，PE △OA ，△△PMN ＝△AEN ，△△PNM ＝△ANE ，△△PNM △△ANE ，△＝，△NE △OB ，△＝，△AN ＝（4﹣m ），△抛物线解析式为y ＝﹣x 2+x +3，△PN ＝﹣m 2+m +3﹣（﹣m +3）＝﹣m 2+3m ，△＝，解得m ＝2．（3）如图2中，在y 轴上 取一点M ′使得OM ′＝，连接AM ′，在AM ′上取一点E ′使得OE ′＝OE ． △OE ′＝2，OM ′•OB ＝×3＝4， △OE ′2＝OM ′•OB ， △＝，△△BOE ′＝△M ′OE ′，△△M ′OE ′△△E ′OB ， △＝＝，△M ′E ′＝BE ′，△AE ′+BE ′＝AE ′+E ′M ′＝AM ′，此时AE ′+BE ′最小 （两点间线段最短，A 、M ′、E ′共线时）， 最小值＝AM ′＝＝．1. 如图，在RT △ABC 中，∠B=90°，AB=CB=2，以点B 为圆心作圆与AC 相切，圆C 的半径为2，点P 为圆B 上的一动点，求PC AP 22的最小值.[答案]：5.2. 如图，边长为4的正方形，内切圆记为⊙O，P是⊙O上一动点，则2PA+PB的最小值为________.[答案]：3. 如图，等边⊙ABC的边长为6，内切圆记为⊙O，P是⊙O上一动点，则2PB+PC的最小值为________.[答案]：2.4. 如图，在Rt△ABC中，∠C=90°，CA=3，CB=4，C的半径为2，点P是C上的一动点，则12 AP PB的最小值为？5. 如图，在平面直角坐标系中，()2,0A，()0,2B，()4,0C，()3,2D，P是△AOB外部第一象限内的一动点，且∠BPA=135°，则2PD PC+的最小值是多少？[答案]6. 如图，Rt△ABC，△ACB＝90°，AC＝BC＝2，以C为顶点的正方形CDEF（C、D、E、F四个顶点按逆时针方向排列）可以绕点C自由转动，且CD＝，连接AF，BD（1）求证：△BDC△△AFC；（2）当正方形CDEF有顶点在线段AB上时，直接写出BD+AD的值；（3）直接写出正方形CDEF旋转过程中，BD+AD的最小值．【解答】（1）证明：如图1中，△四边形CDEF是正方形，△CF＝CD，△DCF＝△ACB＝90°，△△ACF＝△DCB，△AC＝CB，△△FCA△△DCB（SAS）．（2）解：△如图2中，当点D，E在AB边上时，△AC＝BC＝2，△ACB＝90°，△AB＝2，△CD△AB，△AD＝BD＝，△BD+AD＝+1．△如图3中，当点E，F在边AB上时．BD＝CF＝，AD＝＝，△BD+AD＝+．（3）如图4中．取AC的中点M．连接DM，BM．△CD＝，CM＝1，CA＝2，△CD2＝CM•CA，△＝，△△DCM＝△ACD，△△DCM△△ACD，△＝＝，△DM＝AD，△BD+AD＝BD+DM，△当B，D，M共线时，BD+AD的值最小，最小值＝＝．7. （1）如图1，在△ABC中，AB＝AC，BD是AC边上的中线，请用尺规作图做出AB边上的中线CE，并证明BD＝CE：（2）如图2，已知点P是边长为6的正方形ABCD内部一动点，P A＝3，求PC+PD的最小值；（3）如图3，在矩形ABCD中，AB＝18，BC＝25，点M是矩形内部一动点，MA＝15，当MC+MD 最小时，画出点M的位置，并求出MC+MD的最小值．【解答】解：（1）如图1中，作线段AB的垂直平分线MN交AB于点E，连接EC．线段EC即为所求；△AB＝AC，AE＝EC，AD＝CD，△AE＝AD，△AB＝AC，△A＝△A，AD＝AE，△△BAD△△CAE（SAS），△BD＝CE．（2）如图2中，在AD上截取AE，使得AE＝．△P A2＝9，AE•AD＝×6＝9，△P A2＝AE•AD，△＝，△△P AE＝△DAP，△△P AE△△DAP，△＝＝，△PE＝PD，△PC+PD＝PC+PE，△PC+PE≥EC，△PC+PD的最小值为EC的长，在Rt△CDE中，△△CDE＝90°，CD＝6，DE＝，△EC＝＝，△PC+PD的最小值为．（3）如图3中，如图2中，在AD上截取AE，使得AE＝9．△MA2＝225，AE•AD＝9×25＝225，△MA2＝AE•AE，△＝，△△MAE＝△DAM，△△MAE△△DAM，△＝＝＝，△ME＝MD，△MC+MD＝MC+ME，△MC+ME≥EC，△MC+MD的最小值为EC的长，在Rt△CDE中，△△CDE＝90°，CD＝18，DE＝16，△EC＝＝2，△MC+MD的最小值为2．。

“PA+k·PB”型的最值问题【问题背景】“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。

当k值为1时，即可转化为“PA+PB”之和最短问题，就可用我们常见的“将军饮马问题”模型来处理，即可以转化为轴对称问题来处理。

而当k取任意不为1的正数时，若再以常规的轴对称思想来解决问题，则无法进行，因此必须转换思路。

此类问题的处理通常以动点P所在图像的不同来分类，一般分为2类研究。

即点P在直线上运动和点P在圆上运动。

其中点P在直线上运动的类型称之为“胡不归”问题；点P在圆周上运动的类型称之为“阿氏圆”问题。

本文将分别从这两类入手与大家共同探究线段最值问题的解决方案。

【知识储备】线段最值问题常用原理：①三角形的三边关系：两边之和大于第三边，两边之差小于第三边；②两点间线段最短；③连结直线外一点和直线上各点的所有线段中，垂线段最短；【模型初探】（一）点P在直线上运动“胡不归”问题如图1-1-1所示，已知sin∠MBN=k,点P为角∠MBN其中一边BM上的一个动点，点A在射线BM、BN的同侧，连接AP,则当“PA+k·PB”的值最小时，P点的位置如何确定?分析：本题的关键在于如何确定“k·PB”的大小，过点P作PQ⊥BN垂足为Q，则k·PB=PB·sin∠MBN=PQ,∴本题求“PA+k·PB”的最小值转化为求“PA+PQ”的最小值(如图1-1-2)，即A、P、Q三点共线时最小（如图1-1-3），本题得解。

图1-1-1图1-1-2图1-1-3思考：当k值大于1时，“PA+k·PB”线段求和问题该如何转化呢？提取系数k即可哦！！！【数学故事】从前，有一个小伙子在外地学徒，当他获悉在家的老父亲病危的消息后，便立即启程赶路。

由于思乡心切，他只考虑了两点之间线段最短的原理，所以选择了全是沙砾地带的直线路径A→B（如图所示），而忽视了走折线虽然路程多但速度快的实际情况，当他气喘吁吁地赶到家时，老人刚刚咽了气，小伙子失声痛哭。

牛吃草最值问题：1.如图，AB 是⊙O 的直径，AB=8，点M 在⊙O 上，∠MAB=20°，N 是弧MB 的中点，P 是直径AB 上的一动点．若MN=1，则△PMN 周长的最小值为．2.如图,点P 是∠AOB 内一定点，点M 、N 分别在边OA 、OB 上运动，若∠AOB =45°，OP =32，则△PMN 周长的最小值为.3.如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上一动点,点N(6,0)是OB 上的一定点,点M 是ON 中点,∠AOB=30∘，要使PM+PN 最小，则点P 的坐标为.4.如图，Rt △ABC 中，∠ACB=90º，∠CAB=30º， BC=1，将△ABC 绕点B 顺时针转动, 并把各边缩小为原来的一半，得到△DBE ，点A ，B ，E 在一直线上．P 为边DB 上的动点，则AP+CP 的最小值为 ．5.点A 、B 均在由面积为1的相同小矩形组成的网格的格点上，建立坐标系如图所示．若P 是x 轴上使得PA PB -的值最大的点，Q 是y 轴上使得QA+QB 的值最小的点，则OP OQ ⋅＝ ．N M O P B A Ay6.如图，当四边形PABN 的周长最小时，a =．7.矩形OACB 的顶点O 在坐标原点，顶点A 、B 分别在x 轴、y 轴的正半轴上，OA=3，OB =4，D 为边OB 的中点. 若E 、F 为边OA 上的两个动点，且EF =2，当四边形CDEF 的周长最小时，则点F 的坐标为8.如图，在Rt △ABO 中，∠OBA ＝90°，A （4，4），点C 在边AB 上，且＝，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为三角形条件及隐圆最值问题1.如图，在边长为2的菱形ABCD 中，∠A=60°，M 是AD 边的中点，N 是AB 边上一动点，将△AMN 沿MN 所在的直线翻折得到△A′MN ，连接A′C. 则A′C 长度的最小值是.N (a +2,0)P (a ,0)B (4,-1)A (1,-3)O y x F D C B A x y O E F D C B A x y O E2如图，矩形ABCD中，AB=4，BC=2，把矩形ABCD沿过点A的直线AE折叠点D落在矩形ABCD内部的点D处，则CD′的最小值是3.如图，点P是正方形ABCD的对角线BD上的一个动点（不与B、D重合），连结AP，过点B作直线AP的垂线，垂足为H，连结DH，若正方形的边长为4，则线段DH长度的最小值是．4.如图，AB为直径，C为⊙O上一点，其中AB=4，∠AOC=120°，P为⊙O上的动点，取AP中点Q，连CQ，则线段CQ的最大值为5.如图，矩形ABCD中，AC与BD相交于点E，AD：AB＝：1，将△ABD沿BD折叠，点A的对应点为F，连接AF交BC于点G，且BG＝2，在AD边上有一点H，使得BH+EH的值最小，此时BH:CF＝6.如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为_____．7.如图，A(1，0)、B(3，0)，以AB为直径作⊙M，射线OF交⊙M于E、F两点，C为弧AB的中点，D为EF的中点．当射线OF 绕O点旋转时，CD的最小值为________8.如图，点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是______9.AB是半圆O的直径，AB=10，弦AC长为8，点D是弧BC上一个动点，连接AD，作CP⊥AD，垂足为P，连接BP，则BP的最小值是_____10.直线y＝x＋4 分别与x 轴、y 轴相交与点M、N，边长为2 的正方形OABC 一个顶点O 在坐标系的原点，直线AN 与MC 相交与点P，若正方形绕着点O 旋转一周，则点P 到点(0，2)长度的最小值是__________11.如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是x−3与x轴、y轴分别交于A、B两点，P是以C（0，2）为圆心，2为半径的圆上一动点，连结PA、12.如图，已知直线y=34PB．则△PAB面积的最小值是_____．13.如图，C、D是以AB为直径的圆O上的两个动点（点C、D不与A、B重合），在运动过程中弦CD始终保持不变，M是弦CD 的中点，过点C作CP⊥AB于点P．若CD=3，AB=5，PM=x，则x的最大值是14.如图，已知A、B两点的坐标分别为（8，0）、（0，8），点C、F分别是直线x＝﹣5和x轴上的动点，CF＝10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取得最小值时，tan∠BAD的值是15.如图，抛物线y＝x2﹣4与x轴交于A、B两点，P是以点C（0，3）为圆心，2为半径的圆上的动点，Q是线段P A的中点，连结OQ．则线段OQ的最大值是16.如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕着点A旋转，当∠ABF最大时，S△ADE ＝17.如图，在直角坐标系中，已知C（3，4），以点C为圆心的圆与y轴相切．点A、B在x轴上，且OA＝OB．点P为⊙C上的动点，∠APB＝90°，则AB长度的最大值为18.在△ABC中，AB＝4，∠C＝60°，∠A＞∠B，则BC的长的取值范围是19.如图，直线y＝x+1与抛物线y＝x2﹣4x+5交于A，B两点，点P是y轴上的一个动点，当△P AB的周长最小时，S△P AB＝20..如图，△ABC是⊙O的内接三角形，且AB是⊙O的直径，点P为⊙O上的动点，且∠BPC＝60°，⊙O的半径为6，则点P到AC距离的最大值是路径问题：1.如图，AB是⊙O的直径，M、N是（异于A、B）上两点，C是上一动点，∠ACB的角平分线交⊙O于点D，∠BAC 的平分线交CD于点E．当点C从点M运动到点N时，则C、E两点的运动路径长的比是2.如图，在圆心角为90°的扇形OAB中，OB＝2，P为上任意一点，过点P作PE⊥OB于点E，设M为△OPE的内心，当点P从点A运动到点B时，则内心M所经过的路径长为3.如图，在矩形ABCD中，AB＝4，∠DCA＝30°，点F是对角线AC上的一个动点，连接DF，以DF为斜边作∠DFE＝30°的直角三角形DEF，使点E和点A位于DF两侧，点F从点A到点C的运动过程中，点E的运动路径长是4.等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P．若AF=BE，当点E从点A运动到点C时，则点P经过的路径长为．5.如图，边长为2 的正方形ABCD 的两条对角线交于点O，把BA 与CD 分别绕点B 和点C 逆时针旋转相同的角度，此时正方形ABCD 随之变成四边形A′BCD′．设A′C，BD′交于点O′，若旋转了60°，则点O 运动到点O′所经过的路径长为6.已知等边三角形ABC 的边长为4，点D 是边BC 的中点，点E 在线段BA 上由点B 向点A 运动，连接DE，以DE 为边在DE 右侧作等边三角形DEF．设△DEF 的中心为O，则点 E 由点 B 向点 A 运动的过程中，点O 运动的路径长为胡不归型问题：当 k≠1 且 k 为正数时，若点 P 在某条直线上运动时，此时所求的最短路径问题称之为“胡不归”问题．那么对于当“PA + k·PB”的值最小时，点 P 的位置如何确定呢?过点 P 作 PQ⊥BN，垂足为 Q，如图3则 k·PB = PB·sin∠MBN = PQ．因此，本题求“PA + k·PB”的最小值转化为求“PA +PQ”的最小值，即 A，P，Q 三点共线时最小．1.如图，四边形ABCD是菱形，AB=4，且∠ABC=60°,M为对角线BD（不含B点）上任意一点，则AM+1BM的最小值为．22.在△ABC中，AB＝AC＝10，tan A＝2，BE⊥AC于点E，D是线段BE上的一个动点，则CD+BD的最小值是阿氏圆模型问题：已知平面上两点 A，B，则所有满足 PA + k·PB(k≠1，且 k 为正数)，若点 P 的轨迹是一个圆，当点 P 在圆周上运动的类型称之为“阿氏圆”（阿波罗尼斯圆）问题．如图所示，⊙O 的半径为 r，点 A，B 都在圆外，P 为⊙O 上的动点，已知 r = k·OB，连接 PA，PB，则当“PA + k·PB”的值最小时，P 点的位置如何确定?在线段 OB 上截取 OC 使 OC = k·r，则可说明△BPO∽△PCO，即 k·PB = PC．因此，求“PA + k·PB”的最小值转化为求“PA + PC”的最小值，即 A，P，C 三点共线时最小1.已知A(-4，-4)、B(0, 4)、C(0, -6)、 D(0, -1)，AB与x轴交于点E，以点E为圆心，ED长为半径作圆，点M为⊙E上AM的最小值．一动点，求CM+122.如图，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C半径为2，P为圆上一动点，连接AP，BP，则AP+1BP的最小值为．2旋转最值及路径问题：1.如图，点O在线段AB上，OA=1，OB=3，以O为圆心，OA长为半径作⊙O，点M在⊙O上运动，连接MB，以MB为腰作等腰Rt△MBC，使∠MBC=90°，M，B，C三点为逆时针顺序，连接AC，则AC长的取值范围为___________．2.如图，线段AB为⊙O的直径，AB=4，点C为OB的中点，点P在⊙O上运动，连接CP，以CP为一边向上作等边△CPD，连接OD，则OD的最大值为___________．3.如图，在直角坐标系中，已知点A（4，0），点B为y轴正半轴上一动点，连接AB，以AB为一边向下做等边△ABC，连接OC，则OC的最小值为__________4.如图，在Rt△ABC中，AB=BC=2，点P为AB边上一动点，连接CP，以CP为边向下作等腰RT△CPD，连接BD，则BD的最小值为____________．5..如图，在直角坐标系中，已知点A（4，0），点B为直线y=2上一动点，连接AB，以AB为底边向下做等腰Rt△ABC，∠ACB=90°，连接OC，则OC的最小值为__________6.如图，已知点A（3，0），C（0，-4），⊙C的半径为√5，点P为⊙C上一动点，连接AP，若M为AP的中点，连接OM，则OM的最大值为．7．如图，已知△ABC为等腰直角三角形，∠BAC=90°，AC=2，以点C为圆心，1为半径作圆，点P为⊙C上一动点，连结AP，并绕点A顺时针旋转90°得到AP′，连结CP′，则CP′的取值范围是．8.如图，Rt△ABC中，AC=6，BC=8，∠C=90°．点P是AB边上一动点，D是AC延长线上一点，且AC=CD，连接PD，过点D作．则当点P从点A运动到B点时，点E运动的路径长为DE⊥PD，连接PE，且tan∠DPE=252的一个定点，AC⊥x 轴于点M，交直线y=-x 于点N．若点P 是线段ON 上9.如图，点A 是第一象限内横坐标为3的一个动点，∠APB=30°，BA⊥PA，则点P 在线段ON 上运动时，A 点不变，B 点随之运动．当点P 从点O 运动到点N 时，点B 运动的路径长是旋转构图法（补形）问题：常见旋转模型：1.如图，在△ABC 中，AB=AC=32，∠BAC=120°，点D ，E 都在BC 上，∠DAE=60°，若BD=2CE ，则DE 的长为_____．2.在四边形ABCD 中，AD=4，CD ＝3，∠ABC=∠ACB ＝∠ADC=45°，则BD 的长为；3.如图，在△ABC 中，∠ABC=90°，将AB 边绕点A 逆时针旋转90°得到线段AD ，将AC 边绕点C 顺时针旋转90°得到线段CE ，AE 与BD 交于点F ．若DF=2，EF=22，则BC 边的长为____________．A D CB E FDE CB A4.如图，菱形ABCD的对角线AC上有一动点P，BC=6，∠ABC=150°，则线段AP+BP+PD的最小值为5.如图，在△ABC中,∠ABC＝30°，AB＝4 ,BC＝5 , P是△ABC内部的任意一点，连接PA , PB , PC，则PA + PB + PC 的最小值为．。

2020年深圳中考数学压轴题专题总结----胡不归问题为了方便同学们掌握，以下为简化版胡不归问题从前，有一个小伙子在外地学徒，当他获悉在家的老父亲病危的消息后，便立即启程赶路。

由于思乡心切，他只考虑了两点之间线段最短的原理，所以选择了全是沙砾地带的直线路径A→B（如图所示），而忽视了走折线虽然路程多但速度快的实际情况，当他气喘吁吁地赶到家时，老人刚刚咽了气，小伙子失声痛哭。

邻居劝慰小伙子时告诉说，老人弥留之际不断念叨着“胡不归？胡不归？…”。

这个古老的传说，引起了人们的思索，小伙子能否提前到家？倘若可以，他应该选择一条怎样的路线呢？这就是风靡千百年的“胡不归问题”。

例题精讲例1、如图，抛物线y=x2﹣2x﹣3与x轴交于A、B两点，过B的直线交抛物线于E，且tan ∠EBA=，有一只蚂蚁从A出发，先以1单位/s的速度爬到线段BE上的点D处，再以1.25单位/s的速度沿着DE爬到E点处觅食，则蚂蚁从A到E的最短时间是s．【解答】解：过点E作y轴的平行线，再过D点作y轴的平行线，两线相交于点H，如图，∵EH∥AB，∴∠HEB=∠ABE，∴tan∠HED=tan∠EBA==，设DH=4m，EH=3m，则DE=5m，∴蚂蚁从D爬到E点的时间==4（s）若设蚂蚁从D爬到H点的速度为1单位/s，则蚂蚁从D爬到H点的时间==4（s），∴蚂蚁从D爬到E点所用的时间等于从D爬到H点所用的时间相等，∴蚂蚁从A出发，先以1单位/s的速度爬到线段BE上的点D处，再以1.25单位/s的速度沿着DE爬到E点所用时间等于它从A以1单位/s的速度爬到D点，再从D点以1单位/s 速度爬到H点的时间，作AG⊥EH于G，则AD+DH≥AH≥AG，∴AD+DH的最小值为AQ的长，当y=0时，x2﹣2x﹣3=0，解得x1=﹣1，x2=3，则A（﹣1，0），B（3，0），直线BE交y轴于C点，如图，在Rt△OBC中，∵tan∠CBO==，∴OC=4，则C（0，4），设直线BE的解析式为y=kx+b，把B（3，0），C（0，4）代入得，解得，∴直线BE的解析式为y=﹣x+4，解方程组得或，则E 点坐标为（﹣，），∴AQ=，∴蚂蚁从A 爬到G 点的时间==（s ），即蚂蚁从A 到E 的最短时间为s ．故答案为．例2、如图，已知抛物线)4)(2(8-+=x x k y （k 为常数，且0>k ）与x 轴从左至右依次交于A ，B 两点，与y 轴交于点C ，经过点B 的直线b x y +-=33与抛物线的另一交点为D ．（1）若点D 的横坐标为-5，求抛物线的函数表达式；（2）若在第一象限的抛物线上有点P ，使得以A ，B ，P 为顶点的三角形与△ABC 相似，求k 的值；（3）在（1）的条件下，设F 为线段BD 上一点（不含端点），连接AF ，一动点M 从点A 出发，沿线段AF 以每秒1个单位的速度运动到F ，再沿线段FD 以每秒2个单位的速度运动到D 后停止。

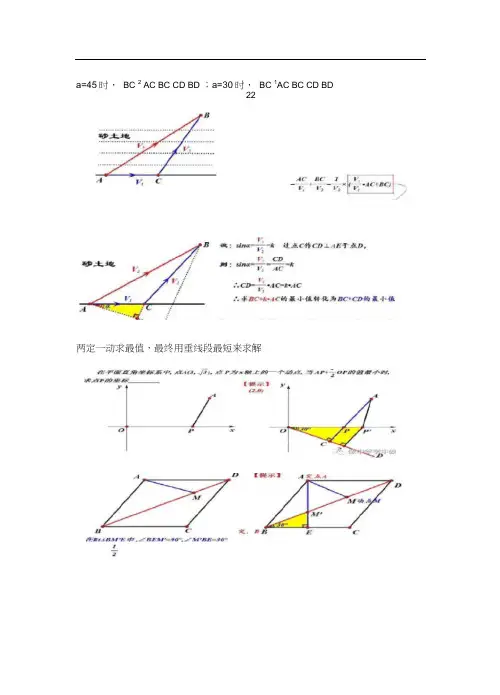
a=45时， BC 2 AC BC CD BD ；a=30时， BC 1AC BC CD BD22两定一动求最值，最终用垂线段最短来求解阿氏圆-两点之间线段最短构造S ΓMC Sd BpC »51^..∙.CΛΓ=J x炉枝・孔"・与WlU 交点HP 刃点" “亠 fP CJ ΛfPMff9 ・■■• • CRCPRP做中字宁中做• ：/>” -J 4~Z ><"点P 刃99匕—必点•詩BP. ・，p*t^⅛Ci ∣lli⅜ BJ«2B>« 2R3Λ0≡K第S 步.【焜示】9522tχ »3«>.斗歩： 笫3F二做中学穿中做•・.PM BP构UrM Szf 次" 9il»Znr rc在BC 上职点3. 快得∙^∙—L rnr J.∙. HM Ii⅛tt<5f ・ ⅛M M 3⅛Z∙J ΨΛA∕∙・PM 」2.:ΛM+ £ PO-Af^PM^JS必诗u.尸.M 三点火SeN 玄小.颠Λff ・ HyNr 中./刀■ W • an■ r∙zr匕在 Q»f Z m■小佢Q C梅系澈不为（的绒段的站个蠟点分别 T例心匕Hlil；接・连接C". CB,il ≡HiMΛtfc[ftc∕>. C"长皮8 辻卸这两务找段长度的比：：C .r>~ . Cr 1座CIr上収点Λ*∙ KfW VP 一2桥耒数不为f的电耳曲跆个* 口分别∖UIQ"4H述牍・嗖按〃化HC I il ΛM I WΛ(⅛WΛ∕F・"ciC∕θ½EP/〒it Mix∣*∣*ten κj(r r∣比十T .年CtRJ AΛYK-換第MJBO如四，在RuMC中，NA5 ・9(f^ ,AC-BC- 2 9以於2为顶点的正方用9DEF(C. D、E. F四个頂点按逆时针方向拮列》可以绕点C 自由恰动，且CD■返•连接—IiD.在证方形CDEF施籽过和中∙Bl)D2∕JK]:^j∩ΛCDM ^ΛCΛD Bl*.Λ2*≡^r r∙7∙r74rΓ'fe<*Λ¾Λ4^;的UBlr) H⅜ 个Ml 点分JMWiR∙DCWIFM： .JrlrCiW C2>. 汁Je川两条GW<∕>ιscfv sCD 2itJtlXRMβBWβ:/V的血K■厶T ；CM J2&d卜圾攻H.位够7齐■：..ev h»>r∕Mr.^MI<∙ ΛWΛΛ∕>.,CD CM DM√5・— ------- ----- ■ ——■・■eι CJ>yj.t∕>.W- — ^z>S∙ f “― 职W、z>. Λ/ Xtyy僅"・【盘WJlW?、5】・.，做中T r G做R厠劝XoyΛ" SM <Λ 1 /»第■步•g步■ 弟*步=宋••海5C兰珈=Z>桁系＜&不％MM J侦Bt旳网TaX点分別耳剧心LfH ⅛fR ,崔渍6"r?Z>；卄XHlFr 条tfcWl<Λ<. O∕>UΛ*it ∙F⅛∙*⅛Λe⅛wLκ^αft9 比ON J"≡"≡ββCP 2在QMfl9莊匸:级上lRΛCΛr・使御.-.OV釜J^*⅛U.VJ ,⅛Mc ⅛f/Λttp 为点"・CA-IOPOF 1「—■ ■”■ IIt 一■—OM R^f 2..Λ-<y*∙√∙z/ mru 135当■、几M三舄其曲MB小.金上AM「存.<≡><∙丹尸Λτ>fr2 ・AnFGX•上旳动点・x⅛ A ∕≠MC上∙CH-I .经Att .3、"&■ Λff-.m 2D匕的娠小俏[ _________________________________ S SfiB示】:B. O. M三τ≡HαtHgfi⅛<M .【窓兀认1上乐7】<fc∕A7∙ □JU∕V G" 圧为C的IF力用"5 内/W A^Λ⅛• /忖-・？• ∙W∕y IZ、的最小伯・I ISzRlD O n：1 ⅛{⅛*"T∙rςr ,⅛^滋貫口乎手匚门伪CQ 2 CΛf Z>M C∙l ~ √ " O 一 "QCQ 2€：H 47> >Γ- [ 17> CZ S Z?Z S€./> Hn> Hn 2ΠE。

婆罗摩笈多、胡不归、阿氏圆——中考几何穿云箭4大专题
婆罗摩笈多、胡不归、阿氏圆，这些名词对于一般的学生确实比较陌生，但是你要问一下学霸，保证给你说得一套一套的。

今天介绍几个比较综合难度较大的几何模型专题：
①平分面积：通过面积之间的等量代换，解决直线平分图形面积的问题。

②胡不归：通过作辅助线构造直角三角形，根据直角三角形中的边角关系转化线段，运用垂线的性质解决线段和的最小值问题。

③阿氏圆：构造共边共角型（母子型）相似模型，运用相似三角形的判定与性质将线段进行转化，根据“两点之间，线段最短”及勾股定理解决两线段和或差的最值问题。

④婆罗摩及多：（以印度数学家命名的）通常运用全等（相似）三角形的判定与性质，已知中点证垂直或已知垂直证中点。

666。

5
小值为------------------------------------------------------------------------（ ）
A.2√5
B.4√5
C.5√5
D.16
2.（内江）如图，在 ∆ACE 中，CA=CE， ∠ CAE=30°，⊙O 经过点 C，且圆的直径 AB 在线段 AE 上。
AC DC
②外角平分线定理：如图，在△ABC 中，AD 平分∠CAE 交 BC 延长线于点 D，则AB = DB。
23
BE 以每秒 1 个单位的速度运动到点 E，再沿线段 ED 以每秒 个单位运动到点 D 停止，问当点 E 的坐标
3
为多少时，点 Q 运动的时间最少？
3
中考数学复习专题 2——“阿氏圆”专题
一、【模型背景】“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。 当 k 值为 1 时，即可转 化为“PA+PB”之和最短问题，就可用我们常见的“将军饮马问题”模型来处理，即可以转化为轴对称问 题来处理。而当 k 取任意不为 1 时，若再以常规的轴对称思想来解决问题，则无法进行，因此必须转换思 路。此类问题的处理通常以动点 P 所在图形的不同来分类，一般分为两类研究。即点 P 在直线上运动和点 P 在圆上运动，其中点 P 在直线上运动的类型称之为“胡不归”问题；点 P 在圆周上运动的类型称之为“阿 氏圆”问题。 二、【模型由来】“阿氏圆”又称“阿波罗尼斯圆”，已知平面上两点 A、B，则所有满足 PA=k·PB 或 PA∶ PB＝k（k≠1）的点 P 的轨迹是一个圆，这个轨迹最早由古希腊数学家阿波罗尼物线对称轴上的一个动点。
① 若平面内存在点 N，使得 A、B、M、N 为顶点的四边形为菱形，则这样的点 N 共有

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题09阿氏圆问题模型建立：已知平面上两点A 、B ,则所有符合＝k （k ＞0且k ≠1）的点P 会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆． 阿氏圆基本解法：构造三角形相似． 模型解读：如图1所示,⊙O 的半径为 r ,点 A 、B 都在⊙O 外,P 为⊙O 上的动点, 已知 r ＝k ·OB ．连接 P A 、PB ,则当“P A ＋k ·PB ”的值最小时,P 点的位置如何确定？1：连接动点至圆心0（将系数不为1的线段两端点分别与圆心相连接）,即连接OP 、OB ； 2：计算连接线段OP 、OB 长度； 3：计算两线段长度的比值OPOB =k ；4：在OB 上截取一点C ,使得OCOP =OPOB 构建母子型相似：5：连接AC ,与圆0交点为P ,即AC 线段长为P A ＋K *PB 的最小值．本题的关键在于如何确定“k ·PB ”的大小,（如图 2）在线段 OB 上截取 OC 使 OC ＝k ·r ,则可说明△BPO 与△PCO 相似,即 k ·PB ＝PC ．∴本题求“P A ＋k ·PB ”的最小值转化为求“P A ＋PC ”的最小值,即 A 、P 、C 三点共线时最小（如图 3）,时AC 线段长即所求最小值．【例1】（2021·全国·九年级专题练习）如图1,在RT△ABC中,∠ACB＝90°,CB＝4,CA＝6,圆C的半径为2,点P为圆上一动点,连接AP,BP,求：BP,①AP+12②2AP+BP,AP+BP,③13④AP+3BP的最小值．【例2】（2022·广东惠州·一模）如图1,抛物线y=ax2+bx−4与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(−1,0),抛物线的对称轴是直线x=3．2(1)求抛物线的解析式；(2)若点P是直线BC下方的抛物线上一个动点,是否存在点P使四边形ABPC的面积为16,若存在,求出点P的坐标若不存在,请说明理由；(3)如图2,过点B作BF⊥BC交抛物线的对称轴于点F,以点C为圆心,2为半径作⊙C,点Q为⊙C上的一个动点,BQ+FQ的最小值．求√24【例3】（2019秋•山西期末）阅读以下材料,并按要求完成相应的任务．已知平面上两点A、B,则所有符合＝k（k＞0且k≠1）的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆．阿氏圆基本解法：构造三角形相似．【问题】如图1,在平面直角坐标系中,在x轴,y轴上分别有点C（m,0）,D（0,n）,点P是平面内一动点,且OP ＝r,设＝k,求PC+kPD的最小值．阿氏圆的关键解题步骤：第一步：如图1,在OD上取点M,使得OM：OP＝OP：OD＝k；第二步：证明kPD＝PM；第三步：连接CM,此时CM即为所求的最小值．下面是该题的解答过程（部分）：解：在OD上取点M,使得OM：OP＝OP：OD＝k,又∵∠POD＝∠MOP,∴△POM∽△DOP．任务：（1）将以上解答过程补充完整．（2）如图2,在Rt△ABC中,∠ACB＝90°,AC＝4,BC＝3,D为△ABC内一动点,满足CD＝2,利用（1）中的结论,请直接写出AD+BD的最小值．【例4】如图,在每个小正方形的边长为1的网格中,△OAB的顶点O,A,B均在格点上,点E在OA上,且点E 也在格点上．（I）的值为；（Ⅱ）是以点O为圆心,2为半径的一段圆弧．在如图所示的网格中,将线段OE绕点O逆时针旋转得到OE′,旋转角为α（0°＜α＜90°）连接E'A,E'B,当E'A+E'B的值最小时,请用无刻度的直尺画出点E′,并简要说明点E'的位置是如何找到的（不要求证明）．一．填空题（共13小题）1．（2022•南召县开学）如图,在△ABC中,∠A＝90°,AB＝AC＝4,点E、F分别是边AB、AC的中点,点P是以A为圆心、以AE为半径的圆弧上的动点,则的最小值为．2．（2021秋•龙凤区期末）如图,在Rt△ABC中,∠C＝90°,AC＝9,BC＝4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则P A+PB的最小值为．3．（2022春•长顺县月考）如图,在Rt△ABC中,∠ACB＝90°,AC＝6,BC＝8,D、E分别是边BC、AC上的两个动点,且DE＝4,P是DE的中点,连接P A,PB,则P A+PB的最小值为．4．（2021秋•梁溪区校级期中）如图,⊙O与y轴、x轴的正半轴分别相交于点M、点N,⊙O半径为3,点A （0,1）,点B（2,0）,点P在弧MN上移动,连接P A,PB,则3P A+PB的最小值为．5．（2021•碑林区校级模拟）如图,在△ABC中,BC＝6,∠BAC＝60°,则2AB+AC的最大值为．6．（2020•武汉模拟）【新知探究】新定义：平面内两定点A,B,所有满足＝k（k为定值）的P点形成的图形是圆,我们把这种圆称之为“阿氏圆”【问题解决】如图,在△ABC中,CB＝4,AB＝2AC,则△ABC面积的最大值为．7．（2020秋•天宁区校级月考）如图,已知菱形ABCD的边长为8,∠B＝60°,圆B的半径为4,点P是圆B上的一个动点,则PD﹣PC的最大值为．8．（2020•溧阳市一模）如图,在⊙O中,点A、点B在⊙O上,∠AOB＝90°,OA＝6,点C在OA上,且OC＝2AC,点D是OB的中点,点M是劣弧AB上的动点,则CM+2DM的最小值为．9．如图,正方形ABCD的边长为4,E为BC的中点,以B为圆心,BE为半径作⊙B,点P是⊙B上一动点,连接PD、PC,则PD+PC的最小值为．10．如图,扇形AOB中,∠AOB＝90°,OA＝6,C是OA的中点,D是OB上一点,OD＝5,P是上一动点,则PC+ PD的最小值为．11．如图所示的平面直角坐标系中,A（0,4）,B（4,0）,P是第一象限内一动点,OP＝2,连接AP、BP,则BP+的最小值是．12．如图所示,∠ACB＝60°,半径为2的圆O内切于∠ACB．P为圆O上一动点,过点P作PM、PN分别垂直于∠ACB的两边,垂足为M、N,则PM+2PN的取值范围为．13．如图,边长为4的正方形,内切圆记为圆O,P为圆O上一动点,则P A+PB的最小值为．二．解答题14．（2022•从化区一模）已知,AB是⊙O的直径,AB＝,AC＝BC．（1）求弦BC的长；（2）若点D是AB下方⊙O上的动点（不与点A,B重合）,以CD为边,作正方形CDEF,如图1所示,若M是DF的中点,N是BC的中点,求证：线段MN的长为定值；（3）如图2,点P是动点,且AP＝2,连接CP,PB,一动点Q从点C出发,以每秒2个单位的速度沿线段CP匀速运动到点P,再以每秒1个单位的速度沿线段PB匀速运动到点B,到达点B后停止运动,求点Q的运动时间t 的最小值．15．（2021•渝中区校级自主招生）如图,在△ABC与△DEF中,∠ACB＝∠EDF＝90°,BC＝AC,ED＝FD,点D 在AB上．（1）如图1,若点F在AC的延长线上,连接AE,探究线段AF、AE、AD之间的数量关系,并证明你的结论；（2）如图2,若点D与点A重合,且AC＝3,DE＝4,将△DEF绕点D旋转,连接BF,点G为BF的中点,连接CG,在旋转的过程中,求CG+BG的最小值；（3）如图3,若点D为AB的中点,连接BF、CE交于点M,CE交AB于点N,且BC：DE：ME＝7：9：10,请直接写出的值．16．（2021•九龙坡区校级模拟）在△ABC中,∠CAB＝90°,AC＝AB．若点D为AC上一点,连接BD,将BD绕点B顺时针旋转90°得到BE,连接CE,交AB于点F．（1）如图1,若∠ABE＝75°,BD＝4,求AC的长；（2）如图2,点G为BC的中点,连接FG交BD于点H．若∠ABD＝30°,猜想线段DC与线段HG的数量关系,并写出证明过程；（3）如图3,若AB＝4,D为AC的中点,将△ABD绕点B旋转得△A′BD′,连接A′C、A′D,当A′D+ A′C最小时,求S△A′BC．17．（2021•沙坪坝区校级模拟）如图1,在四边形ABCD中,AC交BD于点E,△ADE为等边三角形．（1）若点E为BD的中点,AD＝4,CD＝5,求△BCE的面积；（2）如图2,若BC＝CD,点F为CD的中点,求证：AB＝2AF；（3）如图3,若AB∥CD,∠BAD＝90°,点P为四边形ABCD内一点,且∠APD＝90°,连接BP,取BP的中点Q,连接CQ．当AB＝6,AD＝4,tan∠ABC＝2时,求CQ+BQ的最小值．18．（2021·全国·九年级专题练习）如图,Rt△ABC,∠ACB＝90°,AC＝BC＝2,以C为顶点的正方形CDEF （C、D、E、F四个顶点按逆时针方向排列）可以绕点C自由转动,且CD＝√2,连接AF,BD（1）求证：△BDC≌△AFC（2）当正方形CDEF有顶点在线段AB上时,直接写出BD＋√22AD的值；（3）直接写出正方形CDEF旋转过程中,BD＋√22AD的最小值．19．（2022·四川·,在Rt△ABC中,∠C=90∘,CB=4,CA=6,⊙C的半径为2,P为圆上一动点,连接AP、BP,求AP+12BP的最小值．（1）尝试解决：为了解决这个问题,下面给出一种解题思路：如图①,连接CP,在CB上取一点D,使CD=1,则CDCP =CPCB=12．又∠PCD=∠BCP,所以△PCD∽△BCP．所以PDBP=CDCP=12．所以PD=12PB,所以AP+12BP=AP+PD．请你完成余下的思考,并直接写出答案：AP+12BP的最小值为________；（2）自主探索：在“问题提出”的条件不变的前提下,求13AP+BP的最小值；（3）拓展延伸：如图②,已知在扇形COD中,∠COD=90∘,OC=6,OA=3,OB=5,P是CD⌢上一点,求2PA+ PB的最小值．20．（2019·山东·中考真题）如图1,在平面直角坐标系中,直线y＝﹣5x+5与x轴,y轴分别交于A,C两点,抛物线y＝x2+bx+c经过A,C两点,与x轴的另一交点为B（1）求抛物线解析式及B（2）若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积；（3）如图2,若P点是半径为2的⊙B上一动点,连接PC、PA,当点P运动到某一位置时,PC+12PA的值最小,请求出这个最小值,并说明理由．21．（2018·广西柳州·中考真题）如图,抛物线y=ax2+bx+c与x轴交于A(√3,0),B两点（点B在点A的左侧）,与y轴交于点C,且OB=3OA=√3OC,∠OAC的平分线AD交y轴于点D,过点A且垂直于AD的直线l交y轴于点E,点P是x轴下方抛物线上的一个动点,过点P作PF⊥x轴,垂足为F,交直线AD于点H．（1）求抛物线的解析式；（2）设点P的横坐标为m,当FH=HP时,求m的值；（3）当直线PF为抛物线的对称轴时,以点H为圆心,12HC为半径作⊙H,点Q为⊙H上的一个动点,求14AQ+EQ的最小值．【例1】（2021·全国·九年级专题练习）如图1,在RT△ABC中,∠ACB＝90°,CB＝4,CA＝6,圆C的半径为2,点P为圆上一动点,连接AP,BP,求：①AP+12BP,②2AP+BP,③13AP+BP,④AP+3BP的最小值．【例2】（2022·广东惠州·一模）如图1,抛物线y=ax2+bx−4与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(−1,0),抛物线的对称轴是直线x=3．2(1)求抛物线的解析式；(2)若点P是直线BC下方的抛物线上一个动点,是否存在点P使四边形ABPC的面积为16,若存在,求出点P的坐标若不存在,请说明理由；(3)如图2,过点B作BF⊥BC交抛物线的对称轴于点F,以点C为圆心,2为半径作⊙C,点Q为⊙C上的一个动点,BQ+FQ的最小值．求√24【例3】（2019秋•山西期末）阅读以下材料,并按要求完成相应的任务．已知平面上两点A、B,则所有符合＝k（k＞0且k≠1）的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆．阿氏圆基本解法：构造三角形相似．【问题】如图1,在平面直角坐标系中,在x轴,y轴上分别有点C（m,0）,D（0,n）,点P是平面内一动点,且OP ＝r,设＝k,求PC+kPD的最小值．阿氏圆的关键解题步骤：第一步：如图1,在OD上取点M,使得OM：OP＝OP：OD＝k；第二步：证明kPD＝PM；第三步：连接CM,此时CM即为所求的最小值．下面是该题的解答过程（部分）：解：在OD上取点M,使得OM：OP＝OP：OD＝k,又∵∠POD＝∠MOP,∴△POM∽△DOP．任务：（1）将以上解答过程补充完整．（2）如图2,在Rt△ABC中,∠ACB＝90°,AC＝4,BC＝3,D为△ABC内一动点,满足CD＝2,利用（1）中的结论,请直接写出AD+BD的最小值．【分析】（1）在OD上取点M,使得OM：OP＝OP：OD＝k,利用相似三角形的性质以及两点之间线段最短解决问题即可．（2）利用（1）中结论计算即可．【解答】解（1）在OD上取点M,使得OM：OP＝OP：OD＝k,又∵∠POD＝∠MOP,∴△POM∽△DOP．∴MP：PD＝k,∴MP＝kPD,∴PC+kPD＝PC+MP,当PC+kPD取最小值时,PC+MP有最小值,即C,P,M三点共线时有最小值,利用勾股定理得．（2）∵AC＝m＝4,＝,在CB上取一点M,使得CM＝CD＝,∴的最小值为．【例4】如图,在每个小正方形的边长为1的网格中,△OAB的顶点O,A,B均在格点上,点E在OA上,且点E 也在格点上．（I）的值为；（Ⅱ）是以点O为圆心,2为半径的一段圆弧．在如图所示的网格中,将线段OE绕点O逆时针旋转得到OE′,旋转角为α（0°＜α＜90°）连接E'A,E'B,当E'A+E'B的值最小时,请用无刻度的直尺画出点E′,并简要说明点E'的位置是如何找到的（不要求证明）通过取格点K、T,使得OH：OD＝2：3,构造相似三角形将E′B转化为E′H．【分析】（1）求出OE,OB即可解决问题．（2）构造相似三角形把E′B转化为E′H,利用两点之间线段最短即可解决问题．【解答】解：（1）由题意OE＝2,OB＝3,∴＝,故答案为：．（2）如图,取格点K,T,连接KT交OB于H,连接AH交于E′,连接BE′,点E′即为所求．故答案为：通过取格点K、T,使得OH：OD＝2：3,构造相似三角形将E′B转化为E′H,利用两点之间线段最短即可解决问题．一．填空题（共13小题）1．（2022•南召县开学）如图,在△ABC中,∠A＝90°,AB＝AC＝4,点E、F分别是边AB、AC的中点,点P是以A为圆心、以AE为半径的圆弧上的动点,则的最小值为．【分析】在AB上截取AQ＝1,连接AP,PQ,CQ,证明△APQ∽△ABP,可得PQ＝PB,则PB+PC＝PC+PQ,当C、Q、P三点共线时,PC+PQ的值最小,求出CQ即为所求．【解析】如图,在AB上截取AQ＝1,连接AP,PQ,CQ,∵点E、F分别是边AB、AC的中点,点P是以A为圆心、以AE为半径的圆弧上的动点,∴,∵AP＝2,AQ＝1,∴,∵∠P AQ＝∠BAP,∴△APQ∽△ABP,∴PQ＝PB,∴PB+PC＝PC+PQ≥CQ,在Rt△ACQ中,AC＝4,AQ＝1,∴QB＝＝＝．,∴PB+PC的最小值．,故答案为：．2．（2021秋•龙凤区期末）如图,在Rt△ABC中,∠C＝90°,AC＝9,BC＝4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则P A+PB的最小值为．【分析】在AC上截取CQ＝1,连接CP,PQ,BQ,证明△ACP∽△PCQ,可得PQ＝AP,当B、Q、P三点共线时, P A+PB的值最小,求出BQ即为所求．【解析】在AC上截取CQ＝1,连接CP,PQ,BQ,∵AC＝9,CP＝3,∴＝,∵CP＝3,CQ＝1,∴＝,∴△ACP∽△PCQ,∴PQ＝AP,∴P A+PB＝PQ+PB≥BQ,∴当B、Q、P三点共线时,P A+PB的值最小,在Rt△BCQ中,BC＝4,CQ＝1,∴QB＝,∴P A+PB的最小值,故答案为：．3．（2022春•长顺县月考）如图,在Rt△ABC中,∠ACB＝90°,AC＝6,BC＝8,D、E分别是边BC、AC上的两个动点,且DE＝4,P是DE的中点,连接P A,PB,则P A+PB的最小值为．【分析】如图,在CB上取一点F,使得CF＝,连接PF,AF．利用相似三角形的性质证明PF＝PB,根据PF+P A ≥AF,利用勾股定理求出AF即可解决问题．【解析】如图,在CB上取一点F,使得CF＝,连接PF,AF．∵∠DCE＝90°,DE＝4,DP＝PE,∴PC＝DE＝2,∵＝,＝,∴＝,∵∠PCF＝∠BCP,∴△PCF∽△BCP,∴＝＝,∴PF＝PB,∴P A+PB＝P A+PF,∵P A+PF≥AF,AF＝＝＝,∴P A+PB≥,∴P A+PB的最小值为,故答案为．4．（2021秋•梁溪区校级期中）如图,⊙O与y轴、x轴的正半轴分别相交于点M、点N,⊙O半径为3,点A （0,1）,点B（2,0）,点P在弧MN上移动,连接P A,PB,则3P A+PB的最小值为．【分析】在y轴上取点H（0,9）,连接BH,通过证明△AOP∽△POH,可证HP＝3AP,则3P A+PB＝PH+PB,当点P在BH上时,3P A+PB有最小值为HB的长,即可求解．【解析】如图,在y轴上取点H（0,9）,连接BH,∵点A（0,1）,点B（2,0）,点H（0,9）,∴AO＝1,OB＝2,OH＝9,∵,∠AOP＝∠POH,∴△AOP∽△POH,∴,∴HP＝3AP,∴3P A+PB＝PH+PB,∴当点P在BH上时,3P A+PB有最小值为HB的长,∴BH＝＝＝,故答案为：．5．（2021•碑林区校级模拟）如图,在△ABC中,BC＝6,∠BAC＝60°,则2AB+AC的最大值为4．【分析】由2AB+AC＝2（AB+）得,再将AB+AE转化成一条线段BP,可证出∠P是定角,从而点P在△PBC的外接圆上运动,当BP为直径时,BP最大解决问题．【解析】∵2AB+AC＝2（AB+）,∴求2AB+AC的最大值就是求2（AB+）的最大值,过C作CE⊥AB于E,延长EA到P,使得AP＝AE,∵∠BAC＝60°,∴EA＝,∴AB+＝AB+AP,∵EC＝,PE＝2AE,由勾股定理得：PC＝,∴sin P＝,∴∠P为定值,∵BC＝6是定值,∴点P在△CBP的外接圆上,∵AB+AP＝BP,∴当BP为直径时,AB+AP最大,即BP',∴sin P'＝sin P＝,解得BP'＝2,∴AB+AP＝2,∴2AB+AC＝2（AB+AP）＝4,故答案为：4．6．（2020•武汉模拟）【新知探究】新定义：平面内两定点A,B,所有满足＝k（k为定值）的P点形成的图形是圆,我们把这种圆称之为“阿氏圆”【问题解决】如图,在△ABC中,CB＝4,AB＝2AC,则△ABC面积的最大值为．【分析】以A为顶点,AC为边,在△ABC外部作∠CAP＝∠ABC,AP与BC的延长线交于点P,证明△APC∽△BP A,由相似三角形的性质可得BP＝2AP,CP＝AP,从而求出AP、BP和CP,即可求出点A的运动轨迹,再找出距离BC最远的A点的位置即可求解．【解析】以A为顶点,AC为边,在△ABC外部作∠CAP＝∠ABC,AP与BC的延长线交于点P,∵∠CAP＝∠ABC,∠BP A＝∠APC,AB＝2AC,∴△APC∽△BP A,,∴BP＝2AP,CP＝AP,∵BP﹣CP＝BC＝4,∴2AP﹣AP＝4,解得：AP＝,∴BP＝,CP＝,即点P为定点,∴点A的轨迹为以点P为圆心,为半径的圆上,如图,过点P作BC的垂线,交圆P与点A1,此时点A1到BC 的距离最大,即△ABC的面积最大,S△ABC＝BC•A1P＝×4×＝．故答案为：．7．（2020秋•天宁区校级月考）如图,已知菱形ABCD的边长为8,∠B＝60°,圆B的半径为4,点P是圆B上的一个动点,则PD﹣PC的最大值为2．【分析】连接PB,在BC上取一点G,使得BG＝2,连接PG,DG,过点D作DH⊥BC交BC的延长线于H．利用相似三角形的性质证明PG＝PC,再根据PD﹣PC＝PD﹣PG≤DG,求出DG,可得结论．【解析】连接PB,在BC上取一点G,使得BG＝2,连接PG,DG,过点D作DH⊥BC交BC的延长线于H．∵PB＝4,BG＝2,BC＝8,∴PB2＝BG•BC,∴＝,∵∠PBG＝∠CBP,∴△PBG∽△CBP,∴＝＝,∴PG＝PC,∵四边形ABCD是菱形,∴AB∥CD,AB＝CD＝BC＝8,∴∠DCH＝∠ABC＝60°,在Rt△CDH中,CH＝CD•cos60°＝4,DH＝CD•sin60°＝4,∴GH＝CG+CH＝6+4＝10,∴DG＝＝＝2,∵PD﹣PC＝PD﹣PG≤DG,∴PD﹣PC≤2,∴PD﹣PC的最大值为2．8．（2020•溧阳市一模）如图,在⊙O中,点A、点B在⊙O上,∠AOB＝90°,OA＝6,点C在OA上,且OC＝2AC,点D是OB的中点,点M是劣弧AB上的动点,则CM+2DM的最小值为．【分析】延长OB到T,使得BT＝OB,连接MT,CT．利用相似三角形的性质证明MT＝2DM,求CM+2DM的最小值问题转化为求CM+MT的最小值．求出CT即可判断．【解析】延长OB到T,使得BT＝OB,连接MT,CT．∵OM＝6,OD＝DB＝3,OT＝12,∴OM2＝OD•OT,∴＝,∵∠MOD＝∠TOM,∴△MOD∽△TOM,∴＝＝,∴MT＝2DM,∵CM+2DM＝CM+MT≥CT,又∵在Rt△OCT中,∠COT＝90°,OC＝4,OT＝12,∴CT＝＝＝4,∴CM+2DM≥4,∴CM+2DM的最小值为4,∴答案为4．9．如图,正方形ABCD的边长为4,E为BC的中点,以B为圆心,BE为半径作⊙B,点P是⊙B上一动点,连接PD、PC,则PD+PC的最小值为5．【分析】如图,在BC上取一点T,使得BT＝1,连接PB,PT,DT．证明△PBT∽△CBP,推出＝＝,推出PT＝PC,由PD+PC＝PD+PT≥DT＝5,由此可得结论．【解析】如图,在BC上取一点T,使得BT＝1,连接PB,PT,DT．∵四边形ABCD是正方形,∴∠DCT＝90°,∵CD＝4,CT＝3,∴DT＝＝＝5,∵PB＝2,BT＝1,BC＝4,∴PB2＝BT•BC,∴＝,∵∠PBT＝∠PBC,∴△PBT∽△CBP,∴＝＝,∴PT＝PC,∵PD+PC＝PD+PT≥DT＝5,∴PD+PC的最小值为5,故答案为：5．10．如图,扇形AOB中,∠AOB＝90°,OA＝6,C是OA的中点,D是OB上一点,OD＝5,P是上一动点,则PC+ PD的最小值为．【分析】如图,延长OA使AE＝OB,连接EC,EP,OP,证明△OPE∽△OCP推出＝＝,推出EP＝2PC,推出PC+PD＝（2PC+PD）＝（PD+PE）,推出当点E,点P,点D三点共线时,PC+PD的值最小．【解析】如图,延长OA使AE＝OB,连接EC,EP,OP,∵AO＝OB＝6,C分别是OA的中点,∴OE＝12,OP＝6,OC＝AC＝3,∴＝＝,且∠COP＝∠EOP∴△OPE∽△OCP∴＝＝,∴EP＝2PC,∴PC+PD＝（2PC+PD）＝（PD+PE）,∴当点E,点P,点D三点共线时,PC+PD的值最小,∵DE＝＝＝13,∴PD+PE≥DE＝13,∴PD+PE的最小值为13,∴PC+PD的值最小值为．故答案为：．11．如图所示的平面直角坐标系中,A（0,4）,B（4,0）,P是第一象限内一动点,OP＝2,连接AP、BP,则BP+的最小值是．【分析】如图,取点T（0,1）,连接PT,BT．利用相似三角形的性质证明PT＝PB,推出PB+P A＝PB+PT≥BT,求出BT,可得结论．【解析】如图,取点T（0,1）,连接PT,BT．∵T（0,1）,A（0,4）,B（4,0）,∴OT＝1,OA＝4,OB＝4,∵OP＝2,∴OP2＝OT•OA,∴＝,∵∠POT＝∠AOP,∴△POT∽△AOP,∴＝＝,∴PT＝P A,∴PB+P A＝PB+PT,∵BT＝＝,∴PB+PT≥,∴BP+AP≥∴BP+PB的最小值为．故答案为：．12．如图所示,∠ACB＝60°,半径为2的圆O内切于∠ACB．P为圆O上一动点,过点P作PM、PN分别垂直于∠ACB的两边,垂足为M、N,则PM+2PN的取值范围为6﹣2≤PM+2PN≤6+2．【分析】PM+2PN＝2（PM+PN）,作MH⊥PN,HP＝PM,确定HN的最大值和最小值．【解答】解：作MH⊥NP于H,作MF⊥BC于F,∵PM⊥AC,PN⊥CB,∴∠PMC＝∠PNC＝90°,∴∠MPN＝360°﹣∠PMC﹣∠PNC﹣∠C＝120°,∴∠MPH＝180°﹣∠MPN＝60°,∴HP＝PM•cos∠MPH＝PM•cos60°＝PM,∴PN+PM＝PN+HP＝NH,∵MF＝NH,∴当MP与⊙O相切时,MF取得最大和最小,如图1,连接OP,OG,可得：四边形OPMG是正方形,∴MG＝OP＝2,在Rt△COG中,CG＝OG•tan60°＝2,∴CM＝CG+GM＝2+2,在Rt△CMF中,MF＝CM•cos C＝（2+2）×＝3+,∴HN＝MF＝3+,PM+2PN＝2（）＝2HN＝6+2,如图2,由上知：CG＝2,MG＝2,∴CM＝2﹣2,∴HM＝（2﹣2）×＝3﹣,∴PM+2PN＝2（）＝2HN＝6﹣2,∴6﹣2≤PM+2PN≤6+2．13．如图,边长为4的正方形,内切圆记为圆O,P为圆O上一动点,则P A+PB的最小值为2．【分析】P A+PB＝（P A+PB）,利用相似三角形构造PB．【解答】解：设⊙O半径为r,OP＝r＝BC＝2,OB＝r＝2,取OB的中点I,连接PI,∴OI＝IB＝,∵,,∴,∠O是公共角,∴△BOP∽△POI,∴,∴PI＝PB,∴AP+PB＝AP+PI,∴当A、P、I在一条直线上时,AP+PB最小,作IE⊥AB于E,∵∠ABO＝45°,∴IE＝BE＝BI＝1,∴AE＝AB﹣BE＝3,∴AI＝＝,∴AP+PB最小值＝AI＝,∵P A+PB＝（P A+PB）,∴P A+PB的最小值是AI＝＝2．故答案是2．二．解答题14．（2022•从化区一模）已知,AB是⊙O的直径,AB＝,AC＝BC．（1）求弦BC的长；（2）若点D是AB下方⊙O上的动点（不与点A,B重合）,以CD为边,作正方形CDEF,如图1所示,若M是DF的中点,N是BC的中点,求证：线段MN的长为定值；（3）如图2,点P是动点,且AP＝2,连接CP,PB,一动点Q从点C出发,以每秒2个单位的速度沿线段CP匀速运动到点P,再以每秒1个单位的速度沿线段PB匀速运动到点B,到达点B后停止运动,求点Q的运动时间t 的最小值．【分析】（1）AB是⊙O的直径,AC＝BC可得到△ABC是等腰直角三角形,从而得道答案；（2）连接AD、CM、DB、FB,ACD≌△BCF,∠CBF＝∠CAD,证明D、B、F共线,再证明△CMB 是直角三角形,根据直角三角形斜边上的中线等于斜边的一半,即可得证；（3）“阿氏圆”的应用问题,以A为圆心,AP为半径作圆,在AC上取点M,使AM＝1,连接PM,过M作MH⊥AB于H,连接BM交⊙A于P',先证明PM＝,+BP最小,即是PM+BP最小,此时P、B、M共线,再计算BM的长度即可．【解析】（1）∵AB是⊙O的直径,∴∠ABC＝90°,∵AC＝BC,∴△ABC是等腰直角三角形,∠CAB＝45°,∵AB＝4,∴BC＝AB•sin45°＝4；（2）连接AD、CM、DB、FB,如图：∵△ABC是等腰直角三角形,四边形CDEF是正方形,∴CD＝CF,∠DCF＝∠ACB＝90°,∴∠ACD＝90﹣∠DCB＝∠BCF,又AC＝BC,∴△ACD≌△BCF（SAS）,∴∠CBF＝∠CAD,∴∠CBF+∠ABC+∠ABD＝∠CAD+∠ABC+∠ABD＝∠DAB+∠CAB++∠ABC+∠ABD＝∠DAB+45°+45°+∠ABD,而AB是⊙O的直径,∴∠ADB＝90°,∴∠DAB+∠ABD＝90°,∴∠CBF+∠ABC+∠ABD＝180°,∴D、B、F共线,∵四边形CDEF是正方形,∴△DCF是等腰直角三角形,∵M是DF的中点,∴CM⊥DF,即△CMB是直角三角形,∵N是BC的中点,∴MN＝BC＝2,即MN为定值；（3）以A为圆心,AP为半径作圆,在AC上取点M,使AM＝1,连接PM,过M作MH⊥AB于H,连接BM交⊙A于P',如图：一动点Q从点C出发,以每秒2个单位的速度沿线段CP匀速运动到点P,再以每秒1个单位的速度沿线段PB匀速运动到点B,∴Q运动时间t＝+BP,∵AM＝1,AP＝2,AC＝BC＝4,∴＝＝,又∠MAP＝∠P AC,∴△MAP∽△P AC,∴＝＝,∴PM＝,∴+BP最小,即是PM+BP最小,此时P、B、M共线,即P与P'重合,t＝+BP最小值即是BM的长度,在Rt△AMH中,∠MAH＝45°,AM＝1,∴AH＝MH＝,∵AB＝4,∴BH＝AB﹣AH＝,Rt△BMH中,BM＝＝5,∴点Q的运动时间t的最小值为5．15．（2021•渝中区校级自主招生）如图,在△ABC与△DEF中,∠ACB＝∠EDF＝90°,BC＝AC,ED＝FD,点D 在AB上．（1）如图1,若点F在AC的延长线上,连接AE,探究线段AF、AE、AD之间的数量关系,并证明你的结论；（2）如图2,若点D与点A重合,且AC＝3,DE＝4,将△DEF绕点D旋转,连接BF,点G为BF的中点,连接CG,在旋转的过程中,求CG+BG的最小值；（3）如图3,若点D为AB的中点,连接BF、CE交于点M,CE交AB于点N,且BC：DE：ME＝7：9：10,请直接写出的值．【分析】（1）过F作FH⊥AB于H,过E作EG⊥AB于G,结合K字型全等,等腰直角三角形,四点共圆即可得到答案；（2）第二问考察隐圆问题与阿氏圆,取AB的中点O,连接OG,在OB上取OH＝,连接GH,构建相似,转化线段即可得到答案；（3）过点C作BF平行线,点F作BC平行线交于点G；过点G作GH⊥BF于点H,过点K作KI⊥FG,证明△BDF≌△CDE,设BC＝7t,则DE＝9t,ME＝10t,结合勾股定理、相似三角形及解直角三角形的知识进行计算．【解析】（1）线段AF、AE、AD之间的数量关系：,证明如下：过F作FH⊥AB于H,过E作EG⊥AB于G,如图：∵FH⊥AB,EG⊥AB,∠EDF＝90°,∴∠FHD＝∠DGE＝90°,∠FDH＝90°﹣∠EDG＝∠DEG,且DF＝DE,∴△FHD≌△DGE（AAS）,∴FH＝DG＝AD+AG,∵∠ACB＝∠EDF＝90°,BC＝AC,ED＝FD,∴∠F AB＝∠FED＝45°,∴点F、D、A、E四点共圆,∴∠F AE＝∠FDE＝90°,∠EAG＝∠DFE＝45°,∵FH⊥AB,EG⊥AB,∠BAC＝45°,∴△F AH和△EAG为等腰直角三角形,∴AF＝FH,AE＝AG,∴AF＝（AD+AG）＝AD+AG＝AD+AE；（2）取AB的中点O,连接OG,在OB上取OH＝,连接GH,如图：∵G为BF的中点,O为AB中点,∴OG是△ABF的中位线,∴OG＝AF＝DF＝DE＝2,∵AC＝3,∴AB＝AC＝6,OB＝AB＝3,∴＝,而＝＝,∴＝,又∠HOG＝∠GOB,∴△HOG∽△GOB,∴＝＝,∴HG＝BG,∴,要使CG+BG的最小,需CG+HG最小,∴当H、G、C三点共线时,CG+BG的最小,CG+BG的最小值是CH,如图：∵OC＝AB＝3,OH＝,∴CH＝＝,∴CG+BG的最小值是CH＝×＝．（3）过点C作BF平行线,点F作BC平行线交于点G；过点G作GH⊥BF于点H,过点K作KI⊥FG；如图：∵∠BDC＝∠FDE＝90°,∴∠BDC+∠CDF＝∠FDE+∠CDF,即∠BDF＝∠CDE,且CD＝BD,DE＝DF,∴△BDF≌△CDE（SAS）,∴BF＝CE,∠DEC＝∠DFB,∵∠DEC+∠DPE＝90°,∠DPE＝∠MPF,∴∠DFB+∠MPF＝90°,∴∠FME＝90°由BC：DE：ME＝7：9：10,设BC＝7t,则DE＝9t,ME＝10t；∴EF＝DE＝9t,∵CG∥BF,FG∥BC,∴四边形BFGC为平行四边形,∴CE＝BF＝CG,∠ECG＝∠FME＝90°,∴△ECG为等腰直角三角形,∴∠CGE＝45°＝∠GKH,∴△GKH为等腰直角三角形,∴＝,＝＝,＝,∴,∴△CDE∽△GFE,∴∠DCE＝∠FGE,∴；Rt△MFE中,MF＝＝t,∴FK＝MK﹣MF＝ME﹣MF＝10t﹣t,FG＝BC＝7t,设∠GFH＝α,∠KGI＝∠NCD＝β,∴＝,Rt△FKI中,sinα＝,∴,∵GH＝,∴KI＝FK•＝,∴sinβ＝＝＝＝＝,∴．16．（2021•九龙坡区校级模拟）在△ABC中,∠CAB＝90°,AC＝AB．若点D为AC上一点,连接BD,将BD绕点B顺时针旋转90°得到BE,,交AB于点F．（1）如图1,若∠ABE＝75°,BD＝4,求AC的长；（2）如图2,点G为BC的中点,连接FG交BD于点H．若∠ABD＝30°,猜想线段DC与线段HG的数量关系,并写出证明过程；（3）如图3,若AB＝4,D为AC的中点,将△ABD绕点B旋转得△A′BD′,连接A′C、A′D,当A′D+ A′C最小时,求S△A′BC．【分析】（1）通过作辅助线,构造直角三角形,借助解直角三角形求得线段的长度；（2）通过作辅助线,构造全等三角形,设AC＝a,利用中位线定理,解直角三角形,用a的代数式表示CD和HG,即可得CD与HG的数量关系；（3）构造阿氏圆模型,利用两点之间线段最短,确定A'（4）的位置,继而求得相关三角形的面积．【解析】（1）过D作DG⊥BC,垂足是G,如图1：∵将BD绕点B顺时针旋转90°得到BE,∴∠EBD＝90°,∵∠ABE＝75°,∴∠ABD＝15°,∵∠ABC＝45°,∴∠DBC＝30°,∴在直角△BDG中有DG＝＝2,＝,∵∠ACB＝45°,∴在直角△DCG中,CG＝DG＝2,∴BC＝BG+CG＝,∴AC＝BC＝；（2）线段DC与线段HG的数量关系为：HG＝,证明：延长CA,过E作EN垂直于CA的延长线,垂足是N,连接BN,ED,过G作GM⊥AB于M,如图：∴∠END＝90°,由旋转可知∠EBD＝90°,∴∠EDB＝45°∴∠END＝∠EBD＝90°,∴E,B,D,N四点共圆,∴∠BNE＝∠EDB＝45°,∠NEB+∠BDN＝180°∵∠BDC+∠BDN＝180°,∠BCD＝45°,∴∠BEN＝∠BDC,∴∠BNE＝45°＝∠BCD,在△BEN和△BDC中,,∴△BEN≌△BDC（AAS）,∴BN＝BC,∵∠BAC＝90°,在等腰△BNC中,由三线合一可知BA是CN的中线,∵∠BAC＝∠END＝90°,∴EN∥AB,∵A是CN的中点,∴F是EC的中点,∵G是BC的中点,∴FG是△BEC的中位线,∴FG∥BE,FG＝BE,∵BE⊥BD,∴FG⊥BD,∵∠ABD＝30°,∴∠BFG＝60°,∵∠ABC＝45°,∴∠BGF＝75°,设AC＝a,则AB＝a,在Rt△ABD中,AD＝,BD＝BE＝,∴FG＝BE,∴FG＝,∵GM⊥AB,∴△BGM是等腰三角形,∴MG＝MB＝,在Rt△MFG中,∠MFG＝60°,∴MF＝MG,∴MF＝,∴BF＝BM+MF＝,在Rt△BFH中,∠BFG＝60°,∴FH＝＝a,∴HG＝FG﹣FH＝﹣a＝,又∵CD＝＝,∴＝,∴HG＝；（3）设AB＝a,则BC＝,取BC的中点N,连接A′D,A′C,A′N,连接DN,如图3,由旋转可知A′B＝AB＝a,∵＝＝,＝＝,∴,又∠A'BN＝∠CBA',∴△A′BN∽△CBA′,∴＝,∴A'N＝A'C,根据旋转和两点之间线段最短可知,最小,即是A'D+A'N最小,此时D、A'、N共线,即A'在线段DN上,设此时A'落在A''处,过A''作A''F⊥AB于F,连接AA'',如图4,∵D,N分别是AC,BC的中点,∴DN是△ABC的中位线,∴DN∥AB,∵AB⊥AC,∴DN⊥AC,∵∠A＝∠A''F A＝∠A''DA＝90°,∴四边形A''F AD是矩形,∴AF＝A''D,A''F＝AD＝2,∵又A''B＝AB＝4,设AF＝x,在直角三角形A''FB中,A''B2＝A''F2+BF2,∴42＝22+（4﹣x）2,解得x＝．∴此时S△A''BC＝S△ABC﹣S△AA''B﹣S△A''AC＝AB•AC﹣AB•A''F﹣AC•A''D＝×4×4﹣×4×2﹣×4×（4﹣2）＝4﹣4．17．（2021•沙坪坝区校级模拟）如图1,在四边形ABCD中,AC交BD于点E,△ADE为等边三角形．（1）若点E为BD的中点,AD＝4,CD＝5,求△BCE的面积；（2）如图2,若BC＝CD,点F为CD的中点,求证：AB＝2AF；（3）如图3,若AB∥CD,∠BAD＝90°,点P为四边形ABCD内一点,且∠APD＝90°,连接BP,取BP的中点Q,连接CQ．当AB＝6,AD＝4,tan∠ABC＝2时,求CQ+BQ的最小值．【分析】（1）如图1中,过点C作CH⊥BD于H,设EH＝x．利用勾股定理构建方程求出x,即可解决问题．（2）如图2中,延长AF到G,使得AF＝FG,连接DG,CG,延长GC交BD于T,过点C作CH⊥BD于H．想办法证明△AEB≌△ADG（SAS）,可得结论．（3）如图3中,取AD的中点O,连接OP,OB,OC,取OB的中点J,连接QJ,CJ,过点C作CF⊥AB于F,在JB上取一点T,使得JT＝,连接QT,TC．想办法证明△QJT∽△BJQ,推出＝＝＝,推出QT＝BQ,推出CQ+BQ＝CQ+QT≥CT,求出CT,可得结论．【解答】（1）解：如图1中,过点C作CH⊥BD于H,设EH＝x．。

胡不归-阿氏圆问题已知定点A 、B ，要求找一点P ，使aPA+PB 值最小(a 为大于0且不为1的常数)；点P 在直线上运动型称为“胡不归”问题，点P 在圆周上运动型称为“阿氏圆”问题.1.两点之间，线段最短；2.三角形两边之和大于第三边，两边之差小于第三边；3.垂线段最短；构造出新的线段，使其等于aPA ；构造方法：1.作∠α，使sin α=a ；一般a=21、22和23时，作相应30°、45°和60°角，构造出特殊直角三角形；2.构造三角形与已知三角形相似，借助相似比将aPA 转化；注意：一般系数a 满足0＜a ＜1时直接构造；a ＞1时需要先提取系数，如PA+2PB=2（21PA+PB ），PA+2PB=2（22PA+PB ）.一．胡不归问题1.构造含特殊角的直角三角形，将“aPA ”转化已知：如图，A 为直线l 上一点，B 为直线外一点；要求：在直线l 上找一点P ，使得21PA+PB 最小.【分析】利用sin30°=21构造出PH=21PA ，当B 、P 和H 共线时，PH+PB 取得最小值BH ，又当BH ⊥AH 时，BH 取得最小值【解答】过点A 作射线AM ，使∠A=30°（B 、M 位于l 异侧），过点B 作BH ⊥AM 于H ，交直线l 于点P ， 则点P 即为所求，此时21PA+PB 最小，最小值即为问题概述方法原理解题思路线段BH 的长.【小结】1.构造方法可总结为：一作角，二作垂线； 2.系数a 为22、23时，作45°和60°角.典型例题1-1（1）如图1，直线y=x-3与x 轴交于点A ，与y 轴交于点B ，点P 为x 轴上一动点，连接PB ，当P点坐标为_________时，21PA+PB 取得最小值，最小值为__________； （2）如图2，直线y=3x+3与x 轴交于点A ，与y 轴交于点B ，点P 为y 轴上一动点，连接PA ，当P点坐标为________时，2PA+√2PB 取得最小值，最小值为_________.图1 图2【分析】（1）根据模型构造出21PA 找出P 点，借助含30°角的直角三角形解出OP 长和BH 长，从而求出P 点坐标和21PA+PB 的最小值；（2）2PA+√2PB=2（PA+22PB ），与（1）类似的方法求解.【解答】（1）如图，过点A 作射线AC ，与y 轴正半轴交于点C ，使∠OAC=30°，过点B 作BH ⊥AC 于H ，交x 轴于P ，则PH=21PA ，此时12 PA+PB 取得最小值，即为BH 长；已知∠OBP=30°， ∴OP=3OB =3,则P （3，0）又OC=3OA =3，∴BC=3+3，∴BH=23BC=2333+，即12 PA+PB 的最小值为2333+；（2）如图，过点B 作射线BC ，与x 轴的正半轴交于点C ，使∠OBC=45°，过点A 作AH ⊥BC 于H ，交 y 轴于点P ，此时2PA+√2PB 取得最小值， ∵∠BCO=45°，∴AH=√22AC=2√2，∴2PA+√2PB=2AH=4√2，又OP=OA=1，∴P （0，1）；即当P 点坐标（0，1） 时，2PA+√2PB 取得最小值42.【小结】 1.作角时，以定点、定边向“异侧”作射线；2.（2）中提取系数2之后，答案的最小值不要忘记乘2.典型例题1-2如图，P 为正方形ABCD 对角线BD 上一动点，AB ＝2，则AP ＋BP ＋CP 的最小值为（ ）A ．2＋5B ．2＋6C ．4D ．32【分析】由于AP=CP ，AP ＋BP ＋CP=2AP+BP=2（PA+21PB ），从而转化为胡不归模型，结合特殊直角三角形和等面积法可解出该最小值.【解答】∵正方形ABCD 为轴对称图形，∴AP=PC ，∴AP+BP+CP=2AP+BP=2（PA+21PB ），∴即求PA+21PB 的最小值，连接AE ，作∠DBE=30°，交AC 于E ，过A 作AF ⊥BE ， 垂足为F ，在Rt △PBF 中，∵∠PBF=30° ，∴PF=21PB ， ∴PA+21PB 的最小值即为AF 长，易得∠PAO=30°， ∴OP=3AO=36，AP=2OP=362，BP=OB-OP=2-36， ∴PF=21BP=22-66，∴AP+PF=262 ，AP+BP+CP 的最小值为2＋6 ，故选B.【小结】1.求解AF 也可放到△ABE 中，用等面积法计算；2.点P 为△ABC 的“费马点”，感兴趣的读者可查阅相关资料.变式训练1-1如图，一条笔直的公路l 穿过草原，公路边有一消防站A ，距离公路5千米的地方有一居民点B ，A 、B 的直线距离是13千米.一天，居民点B 着火，消防员受命欲前往救火，若消防车在公路上的最快速度是80千米/小时，而在草地上的最快速度是40千米/小时，则消防车在出发后最快经 小时可到达居民点B.(消防车可从公路的任意位置进入草地行驶)135B变式训练1-2如图，菱形ABCD 的对角线AC 上有一动点P ，BC ＝6，∠ABC＝150°，则线段 AP ＋BP ＋PD 的最小值为___________2.构造相似三角形，借助相似比将“aPA ”转化 典型例题2-1如图，△ABC 在直角坐标系中，AB=AC ，A （0，22）， C （1，0），D 为射线AO 上一点，一动点P 从A 出发，运动路径为线段AD 、DC ，点P 在AD 上的运动速度是在CD 上的3倍，要使整个运动时间最少，则点D 的坐标应为_______【分析】设CD 上速度为v ，AD 上速度为3v ，则全程时间t=v CD vAD+3=)(311CD AD v +，当31AD+CD 最小时，总时间最少；分析条件知CO=31AC ，过点D 作DH ⊥AC 于H ，构造△ADH 和△ACO 相似，则DH=31AD ，又CD=BD ，则需DH+BD 最小，此时B 、D 、H 共线且BH ⊥AC ，借助相似易得点D 坐标.【解答】如图，作DH ⊥AC 于点H ，交AO 于D ，此时整个运动时间最少，易证△BOD ∽△AOC ，则OAOBOC OD ==221，∴OD=221OC =42，∴D （0，42）【小结】1.首先表示出时间和各段路程的关系；2.找出图中含有两边之比等于系数a 的三角形；3.构造相似三角形求解.变式训练2-1如图，抛物线y=﹣x 2+x+3与x 轴交于点A ，点B ，与y 轴交于点C ，点D 与点C 关于x 轴对称，点P 是x 轴上的一个动点，设点P 的坐标为（m ，0），过点P 作x 轴的垂线l 交抛物线于点Q ． （1）求直线BD 的解析式；（2）当点P 在线段OB 上运动时，直线l 交BD 于点M ，当△DQB 面积最大时，在x 轴上找一点E ，使QE+EB 的值最小，求E 的坐标和最小值．二．阿氏圆问题一般构造“子母”型相似三角形，借助相似比将“aPA ”转化 典型例题3-1如图，Rt △ABC 中，∠ACB=90°，AC=3，BC=4，D 为直角边AC 上一 点，且CD=2，将CD 绕着点C 顺时针旋转α（0＜α＜90°），D'为 点D 的对应点，连接AD'和BD'，则AD'+21BD'的最小值是________. 【分析】D'在以C 为圆心，半径为2的圆弧上运动，△CD'B 中，CD'=21BC ，据此在CB 上截取CF=21CD'=1，构造△CFD'∽△CD'B ，将21BD'转化为D'F ，即求AD'+D'F 的最小值，A 、D'、F 共线时其值最小，由勾股定理易求该值.【解答】在线段CB 上截取CF=21CD'=1，∴21==''CBD C D C CF ，又∵∠FCD'=∠D'CB ，∴△CFD'∽△CD'B ，∴21=''B D FD ,即D'F=21BD'，要使AD'+21BD'最小，则需AD'+D'F 最小，此时A 、D'、F 三点共线，AD'+D'F 的最小值即为AF 长，在Rt △ACF 中， AF=22CF AC +=2213+=10， 即AD'+21BD'的最小值是10.变式训练3-1如图1，抛物线y=ax2﹣6ax+6（a≠0）与x轴交于点A（8，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜8），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM ⊥AB于点M．（1）分别求出直线AB和抛物线的函数表达式．（2）设△PMN的面积为S1，△AEN的面积为S2，若S1：S2=36：25，求m的值．（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B．①在x轴上找一点Q，使△OQE′∽△OE′A，求出Q点坐标．②求BE′+AE′的最小值.变式训练3-2在平面直角坐标系中，A（2，0），B（4，0），C（0，4），D（3，2），P是△AOC外部的第一象限内一动点，且∠CPA﹦135°，则2PD﹢PB的最小值是．中考真题1.如图，AB 为⊙O 的直径，点C 是⊙O 上的一点，AB=8cm ，∠A=30°，点D 是弦AC 上的一点，动点P 从点C 沿CA 以2cm/s 的速度向点D 运动，再沿DO 以1cm/s 的速度向点O 运动，设点P 在整个运动过程中的时间为t ，则t 的最小值是 s ．2.如图，二次函数y=ax 2+bx+c 的图像经过点A （-1，0），B （0，-3）、C （2，0），其对称轴与x轴交于点D 。

“PA+k·PB”型的最值问题【问题背景】“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。

当k值为1时，即可转化为“PA+PB”之和最短问题，就可用我们常见的“饮马问题”模型来处理，即可以转化为轴对称问题来处理。

而当k取任意不为1的正数时，若再以常规的轴对称思想来解决问题，则无法进行，因此必须转换思路。

此类问题的处理通常以动点P所在图像的不同来分类，一般分为2类研究。

即点P在直线上运动和点P在圆上运动。

其中点P在直线上运动的类型称之为“胡不归”问题；点P在圆周上运动的类型称之为“阿氏圆”问题。

本文将分别从这两类入手与大家共同探究线段最值问题的解决方案。

【知识储备】线段最值问题常用原理：①三角形的三边关系：两边之和大于第三边，两边之差小于第三边；②两点间线段最短；③连结直线外一点和直线上各点的所有线段中，垂线段最短；【模型初探】（一）点P在直线上运动“胡不归”问题如图1-1-1所示，已知sin∠MBN=k,点P为角∠MBN其中一边BM上的一个动点，点A在射线BM、BN的同侧，连接AP,则当“PA+k·PB”的值最小时，P点的位置如何确定?分析：本题的关键在于如何确定“k·PB”的大小，过点P作PQ⊥BN垂足为Q，则k·PB=PB·sin∠MBN=PQ,∴本题求“PA+k·PB”的最小值转化为求“PA+PQ”的最小值(如图1-1-2)，即A、P、Q三点共线时最小（如图1-1-3），本题得解。

图1-1-1 图1-1-2 图1-1-3动态展示：见GIF格式！思考：当k值大于1时，“PA+k·PB”线段求和问题该如何转化呢？提取系数k即可哦！！！【数学故事】从前，有一个小伙子在外地学徒，当他获悉在家的老父亲病危的消息后，便立即启程赶路。

由于思乡心切，他只考虑了两点之间线段最短的原理，所以选择了全是沙砾地带的直线路径A→B（如图所示），而忽视了走折线虽然路程多但速度快的实际情况，当他气喘吁吁地赶到家时，老人刚刚咽了气，小伙子失声痛哭。

《胡不归与阿氏圆两类系数不为1的最值小例》（下集）《上集》讲的是一种特殊的系数不为1的最值问题，名叫“胡不归”，同学们你们记住了吗？会解决这个模型了吗？下面再提供一个表面上与其很类似的问题，但本质不同，称之为“阿波罗尼斯圆”模型，简称“阿氏圆”问题！（“阿氏圆”问题）问题2：如图2，已知点B（8，0），C（0，6），半径为3的⊙O上有一动点P，求PB+1/2*PC的最小值.“美丽的图形会说话”（朋友语）！先呈上解决此题的终极图形，如图2-1，同学们可对照此图先自行参悟，然后再听我娓娓道来！简析：此题依然是一个“两定一动型”最值问题，且动点P被“绑在”了半径为3的⊙O上运动，动点P的本质特征也就是⊙O的本质特征，即到原点O的距离始终为3，解题的关键肯定也要抓住这个本质特征；此题让人望而却步的，还是在不为1这个系数上，即“1/2”，如何处理“1/2”成为了解题的难点；回顾上面的“胡不归”模型，里面也有不为1的系数，我们利用“构造三角函数”的联想机制，成功将系数转化为1；其间之所以能“构造三角函数”，是因为动点从一个定点出发先沿着一条定直线运动，构造的关键也是抓住这条定直线及其上的这一个定点，即过定直线上的定点向这条定直线的某一侧（视具体情况而定）作一个锐角，使其正弦值等于要处理的系数，从而将系数顺利转化为1；那么本题可不可以同样处理呢？显然不行，动点P在一个圆上运动，该怎么构造三角函数啊！看来此路不通，那就再作其他联想吧！想啊……想啊……，想到目标是要处理“1/2*PC”，与点B无关，那就先擦去PB，减少题目中的干扰线条，如图2-2所示，将目光就聚焦在一点，即PC上；第一步（连接半径，突出本质）：刚刚说过，动点P被“绑在”了半径为3的⊙O上，动点P的本质特征是其到原点O的距离始终为定值3，转化“1/2*PC”的关键肯定也要抓住这个本质特征；如图2-2，连接半径OP，发现题目的特殊性，即OP=3且OC=6，这是本题的“巧合”，一般此种题型都具备这样的特殊性，同学们要多尝试、多联想；至此，此题得到完美解决！我们不妨再回头看看一开始的“终极图形”，即图2-1，再次深刻反思、体会所谓“阿氏圆”的解题策略：解题后反思：上述是两种不同的系数不为1的最值问题，其解决策略的共通之处都是想办法处理不为1的系数，将其化为1；但转化的方式略有不同：“胡不归”问题是转化定直线上的定点作定角，使这个定角的正弦值等于题中速度之比（小速度：大速度），可顺利将系数都处理为1；而“阿氏圆”是抓住动点P的本质，即到圆心O的距离为半径，连接圆心O与动点P以及圆心O与系数不为1相关的那个定点C，再借助题目中数据的“巧合性”，即刚刚两个连线段的长度之比恰为要处理的系数，构造一组“母子型”相似，成功将系数化为1！凡事都有“异同”，同学们要去相互类比，联想比较，才能达到应用自如之功力！。

“PA+k·PB”型的最值问题---孙洋清【问题背景】“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。

当k值为1时，即可转化为“PA+PB”之和最短问题，就可用我们常见的“饮马问题”模型来处理，即可以转化为轴对称问题来处理。

而当k取任意不为1的正数时，若再以常规的轴对称思想来解决问题，则无法进行，因此必须转换思路。

此类问题的处理通常以动点P所在图像的不同来分类，一般分为2类研究。

即点P在直线上运动和点P在圆上运动。

其中点P在直线上运动的类型称之为“胡不归”问题；点P在圆周上运动的类型称之为“阿氏圆”问题。

本文将分别从这两类入手与大家共同探究线段最值问题的解决方案。

【知识储备】线段最值问题常用原理：①三角形的三边关系：两边之和大于第三边，两边之差小于第三边；②两点间线段最短；③连结直线外一点和直线上各点的所有线段中，垂线段最短；【模型初探】（一）点P在直线上运动“胡不归”问题如图1-1-1所示，已知sin∠MBN=k,点P为角∠MBN其中一边BM上的一个动点，点A在射线BM、BN的同侧，连接AP,则当“PA+k·PB”的值最小时，P点的位置如何确定?分析：本题的关键在于如何确定“k·PB”的大小，过点P作PQ⊥BN垂足为Q，则k·PB=PB·sin∠MBN=PQ,∴本题求“PA+k·PB”的最小值转化为求“PA+PQ”的最小值(如图1-1-2)，即A、P、Q三点共线时最小（如图1-1-3），本题得解。

图1-1-1 图1-1-2 图1-1-3动态展示：见GIF格式！思考：当k值大于1时，“PA+k·PB”线段求和问题该如何转化呢？提取系数k即可哦！！！【数学故事】从前，有一个小伙子在外地学徒，当他获悉在家的老父亲病危的消息后，便立即启程赶路。

由于思乡心切，他只考虑了两点之间线段最短的原理，所以选择了全是沙砾地带的直线路径A→B（如图所示），而忽视了走折线虽然路程多但速度快的实际情况，当他气喘吁吁地赶到家时，老人刚刚咽了气，小伙子失声痛哭。

专题2-5最值模型之阿氏圆与胡不归知识点梳理模块一胡不归模型【题型1】胡不归模型·已有相关角直接作垂线【题型2】胡不归模型·构造相关角再作垂线【题型3】胡不归模型·取最值时对其它量进行计算模块二阿氏圆模型【题型4】点在圆外：向内取点（系数小于1）【题型5】点在圆内：向外取点（系数大于1）【题型6】一内一外提系数【题型7】隐圆型阿氏圆知识点梳理一、胡不归模型讲解如图，一动点P 在直线MN 外的运动速度为V 1，在直线MN 上运动的速度为V 2，且V 1＜V 2，A 、B 为定点，点C 在直线MN 上，确定点C 的位置使21AC BCV V 的值最小．2MM121121=V AC BC BC AC V V V V，记12V k V ，即求BC ＋kAC 的最小值．构造射线AD 使得sin ∠DAN ＝k ，CH /AC ＝k ，CH ＝kA C ．将问题转化为求BC ＋CH 最小值，过B 点作BH ⊥AD 交MN 于点C ，交AD 于H 点，此时BC ＋CH 取到最小值，即BC ＋kAC 最小．二、阿氏圆模型讲解【模型来源】所谓阿圆，就是动点到两定点距离之比为定值，那么动点的轨迹就是圆，这个圆，称为阿波罗尼斯圆，简称为阿圆．其本质就是通过构造母子相似，化去比例系数，转化为两定一动将军饮马型求最值，难点在于如何构造母子相似．【模型建立】如图1所示，⊙O 的半径为R ，点A 、B 都在⊙O 外，P 为⊙O 上一动点，已知R ＝25OB ，连接PA 、PB ，则当“PA ＋25PB ”的值最小时，P 点的位置如何确定？解决办法：如图2，在线段OB上截取OC使OC＝25R，则可说明△BPO与△PCO相似，则有25PB＝PC。

故本题求“PA＋25PB”的最小值可以转化为“PA＋PC”的最小值，其中与A与C为定点，P为动点，故当A、P、C三点共线时，“PA＋PC”值最小。

模块一胡不归模型【题型1】胡不归模型·已有相关角直接作垂线2023·西安·二模2023·保定·一模2．如图，在矩形ABCD中，对角线2AM ．点P为线段OB（1）OBC2023·湘西·中考真题4．如图，AB AC ，A 为A D C ，在AD 最少时，D 的坐标为2023·江苏宿迁中考模拟5．如图，二次函数22y ax ax 23．点P 为直线l 上一动点，P ，再以每秒1个单位长度的速度沿2023·四川自贡·统考中考真题2023·成都市七中校考7．如图，在矩形ABCD 中，AB EF 翻折，点A 的对应点A 动点，则55EM A M的最小值为【题型2】胡不归模型·构造相关角再作垂线8．如图，在长方形ABCD 中，AB 2BE DE 的最小值为2023·广西二模9．如图所示，在ABC 中，30A ，M 为线段AB 上一定点，P 为线段AC 上一动点．当点P 在运动的过程中，满足12PM AP的值最小时，则APM ．10．如图，90ACB ，2AC ，4AB ，点P 为AB 上一点，连接PC ，则12PC PB的最小值为3．11．如图，AC 是圆O 的直径，4AC ，弧120BA ，点D 是弦AB 上的一个动点，那么12OD BD的最小值为()A ．32B ．3C ．312D ．1312．如图，在ABC 中，15A ，10AB ，P 为AC 边上的一个动点（不与A 、C 重合），连接BP ，则22AP PB 的最小值是()D．8A．B．C【题型3】胡不归模型·取最值时对其它量进行计算2023·广东深圳·统考三模15．如图，在△ACE中，（1）试说明CE是⊙O（2）若△ACE中AE边上的高为16．如图，矩形ABCD的对角线AC，BD相交于点O，COD关于CD的对称图形为CED．（1）求证：四边形OCED是菱形；（2）连接AE ，若6AB cm ，BC ．①求sin EAD 的值；②若点P 为线段AE 上一动点（不与点A 重合），连接OP ，一动点Q 从点O 出发，以1/cm s 的速度沿线段OP 匀速运动到点P ，再以1.5/cm s 的速度沿线段PA 匀速运动到点A ，到达点A 后停止运动，当点Q 沿上述路线运动到点A 所需要的时间最短时，求AP 的长和点Q 走完全程所需的时间．17．抛物线2y x bx c 与x 轴交于A 、B 两点，与y 轴交于点C ，且(1,0)B ，(0,3)C ．（1）求抛物线的解析式；（2）如图，点D 是抛物线的顶点，将抛物线沿CD 方向平移，使点D 落在点D 处，且2DD CD ，点M 是平移后所得抛物线上位于D 左侧的一点，//MN y 轴交直线OD 于点N ，连结CN ．当5D N CN 的值最小时，求MN 的长．模块二阿氏圆模型【题型4】点在圆外：向内取点（系数小于1）18．如图，已知正方ABCD 的边长为6，圆B 的半径为3，点P 是圆B 上的一个动点，则12PD PC的最大值为_______．A B CDP19．如图，在Rt ABC 中，90ACB ，4CB ，6CA ，圆C 的半径为2，点P 为圆上一动点，连接AP ，BP ．求①12AP BP；②2AP BP ；③13AP BP ；④3AP BP 的最小值．B为______．DCBA22．如图，等边三角形ABC边长为43，圆O是△ABC的内切圆，P是圆O上一动点，连接PB、PC，则BP＋12CP的最小值为______________．CB23．如图，在平面直角坐标系中，M(6，3)，N(10，0)，A(5，0)，点P为以OA为半径的圆O上一动点，则PM＋12PN的最小值为_______________2023·山东烟台·统考中考真题25．如图1，抛物线y ＝ax 2＋(a ＋3)x ＋3与x 轴交于点A （4，0），与y 轴交于点B ，点E 是线段OA上的一个动点，过点E 作x 轴的垂线交直线AB 于点N ，交抛物线于点P ，过点P 作PM ⊥AB 于点M ．（1）求抛物线的函数表达式；（2）当MN NE ＝65时，求点E 的坐标；（3）如图2，在（2）条件下，将线段OE 绕点O 逆时针旋转得到OE′，连接E′A 、E′B ，求E′A ＋23E′B 的最小值．yB O A EP MN 图1y B O AE P M N图2E′【题型5】点在圆内：向外取点（系数大于1）27．如图，∠AOB =90________．B A PO28．已知扇形COD 中，∠COD =90°，OC =6，OA =3，OB =5，点P 是弧CD 上一点，2PA +PB 的最小值为________．O DAB P C【题型6】一内一外提系数29．如图，在ABC 中，90ABC ，26AB BC ，1BD ，P 在以B 为圆心3为半径的圆上，则6AP PD 的最小值为【解答】解：在AB 上取点E ，使32BE ，26AB BC ∵， 12BP BE AB BP ，PBE ABP ∵，PBE ABP ∽， 12PE BP PA AB ，12PE PA，在BD 延长线上取9BF ，1BD ∵，则3BF BP PB BD，又PBD FBP ∵，PBD FBP ∽， 3PF PB PD BD，3PF PD ，162(3)2()2PA PD PA PD PE PF ， 当P 为EF 和圆的交点时PE PF 最小，即6PA PD 最小，且值为2EF ，3372EF ∵，6PA PD 的最小值为2EF故答案为：．30．如图，正方形ABCD 边长为4，L 是CD 的中点，Y 在C |YA 的最大值是YA的最小值是【题型7】隐圆型阿氏圆2023·咸阳·三模2023·宿迁·三模32．如图，在平面直角坐标系中，135APB，则33．如图，在Rt ABC中，90ACB，6AC ，8BC ，D、E分别是边BC、AC上的两个动点，且4DE ，P是DE的中点，连接PA，PB，则14PA PB的最小值为．35．如图，在平面直角坐标系中，(2,0)D，P是AOBB、(4,0)A、(0,2)C、(3,2)外部的第一象限内一动点，且135BPA的最小值是．，则2PD PC。

浅谈线段之和“胡不归”仃灯破故事,说的兄卜身在他乡的小伙子,得知父弟•. 一的消息后便II仪辻路回-• 然|厲当他气喘吁吁地来到父亲的面前时.老人別刚咽气了人们告诉仙.・右:弥・老人在不断喃喃地叨念：“胡不归?胡不归? ”早期的科学家曾为这则占老的传说中的小伙子设想了一*路线。

(如卜•图)A是出发地，B 是H的地：AC &•条驿(・而驿|r徉H的地的・侧是沙地。

为了急切回家.小秋了选择了直线路程AB。

但足，他忽略了在驿道上行走要比任妙土地•苦“•走快的迖•囚素c如果他能选择•乂介适的路线(尽管这条珞线长一些.但是违度町以加快)，足可以提前抵迖栄门的，那么.址' 支足那条路线呢？显然.根4W两种路廊的棚伽在共上街左的速度值•町以右AC I•选定点D,小伙了从A走到D,然厉从D折往B,可电最早到达B・用现代的科学语言表迖，就是：石在驿道I •彳J走的速度为％,化沙地I.I JA L的速度为V：,即求^+― 的故小仇例題1、如图.P为止方形ABCD对角纹BD I.动点.若AB — 2・则AP I BP CP的最小值为_____解析:•••正方形ABCD为轴对称图形• •/\P=PCAAP+BPK：P=2AP+BP= 2(AP+- BP)2•••即求AP+丄BP的最小値2J接卜尢就是套路我们要构造一个丄3P；I俅2连接AU,作ZDBE=3()。

，交AC于&过A作AHI BE・垂足为I； ffiRtA PBF 中,・.・ZPBI；=3()>2山此我们把构造出來了—•••解R 角M AO=B(>=72AP^-BP 的展小値即为AF 线段的KMVVZlL\ll=45\ ZAEIi=6()恨据面枳注.丄人£・B0二丄〃£2 2求出 A V^yfl-y/b（此外本題费马点亦可）例题2【题21】如图1所示.点川为口线/外一定点，点伏C 为比线/上M 宦点.且,1〃 = 2・ZJZ?C = 15°.点〃为口线/上的动点，请确定点P 的 位世.便"+丄/炉址小.并求出这个*4小値 7B AB住初二〃"彳从 总结步骤:【解析】如图2,将II 线/绕点〃逆时针旋转30°貳厂的位歆 过点 A^ADL 厂交/于点P',在宜线/上収任意点P,作PELT 于点E,在 直角三角形〃妙中，PE =丄3P,冋理刖2 2AP+丄 BP = AP + PE 工 AD = AP4 严D 二人P4 ' BP',当点 P 与点2 2P'重合时取等号•在RZPD 中.BP'= “ 屮=2&cos 30° y/3 3T范当列建时，gp'重合，如悴取得虽小值®笫 步：将所求线段和改写为PA+’PB 的形式（上VI ） ni m小••炽/1PB 的」偵.PA #J 畀侧.构進-•个如度cu 便得sina=一 m第三步：过A 作第二妙所构适的角的 边匝线，该匝线段即为所求赧小伯 第四步,计算即诃模型具体归纳如下:茨:PA+n/mPB(问JS关键处H摊n/m 这个分数梅造岀sinzCBP=n/mlK94« PA4-n/mPB= AP・PD再利用垂线段最炷即可练习1如岸，条笔直的公路I穿过草原，公路边存消防站A，加离公路5 T•米的也方居尺点B・A、B的直线距离13 TX.吠，居尺点B看火，消防员受命欲前往救火,若消防车右:介路I的杲快速度是80 T米〃卜时・而右:草地I •的呆快速度是40 T米〃卜时.则•消防车在出发臥加快经___ 小时町到达居尺点B.S怙琨酥：汨鮎河从公路的沖逵入草如了絞.)练习2【题22】如图I,在平面直角坐标系中，己知A (0.4),〃(-10),在皿上有-动点G,求BG+护的最小值.练习3（北京东城区1观年离考備25》如囤假设河的一令岸边为言线X/iCl.vr;于c, s B. 2＞在"V上，现离将货切心处运（£月处，经陆路3与水路DB・已知4C=[0公塾BC=SO 公里，又陆跻单位距离的运扫罡水路运捻的2倍.为使运腰少，D点应选在蹈5C卢耳多运M?・练习4如用，AABC &&f（]坐杯系屮，AB-AC, A （0, 2近）.C（1, 0）, D 为射线AO卜.一点.一动点P从A出发.运动路径为ATDTC.点P在AD上的运动速度是在CD上的3倍•咚使整个运动时间最少•则点D的坐标应为________________练习5 如图,菱形ABCD的对角线AC上有-动点P・BC=6, ZABCJ50•，则线段AP+BP+PD 的最小值为练习6如图.在丫商直角坐标系中，二次函数y=ax2-bx^c的图象经过点A （-1, 0〉. B CO. ■近）• C （2. 0）,其对称轴九I交丁点D（1）求二次函数的表达式及其顶点坐标；2）若P为y轴上的一个动点，连接PD.则±PB+PD的最小值为 :练习7如I絹&AACE屮.CA=CE, ZCAE=30% G）0经过点C,且圆的直径AB任线段AE上.（1）试说明CE是O0的切线：（2＞若厶ACE«；'AE边上的高为h,试用含h的代数式衣示©0的直径AB：（3）设点D是线段AC上任总一点（不介端点），连接0D,为丄CD+OD的最小2值为6E・J・求GO的直径AB的长.附加（阿氏圆问题）何氏冏也是彤WA Y—PB的形式（上VI）瓜终还是化分为整。