8__第十一章_压杆稳定问题

第十一章压杆的稳定承受轴向压力的杆，称为压杆。

如前所述，直杆在轴向压力的作用下，发生的是沿轴向的缩短，杆的轴线仍然保持为直线，直至压力增大到由于强度不足而发生屈服或破坏。

直杆在轴向压力的作用下，是否发生屈服或破坏，由强度条件确定，这是我们已熟知的。

然而，对于一些受轴向压力作用的细长杆，在满足强度条件的情况下，却会出现弯曲变形。

杆在轴向载荷作用下发生的弯曲，称为屈曲，构件由屈曲引起的失效，称为失稳（丧失稳定性）。

本章研究细长压杆的稳定。

§11.1 稳定的概念物体的平衡存在有稳定与不稳定的问题。

物体的平衡受到外界干扰后，将会偏离平衡状态。

若在外界的微小干扰消除后，物体能恢复原来的平衡状态，则称该平衡是稳定的；若在外界的微小干扰消除后物体仍不能恢复原来的平衡状态，则称该平衡是不稳定。

如图11.1所示，小球在凹弧面中的平衡是稳定的，因为虚箭头所示的干扰（如微小的力或位移）消除后，小球会回到其原来的平衡位置；反之，小球在凸弧面上的平衡，受到干扰后将不能回复，故其平衡是不稳定的。

(a) 稳定平衡图11.1 稳定平衡与不稳定平衡上述小球是作为未完全约束的刚体讨论的。

对于受到完全约束的变形体，平衡状态也有稳定与不稳定的问题。

如二端铰支的受压直杆，如图11.2(a)所示。

当杆受到水平方向的微小扰动（力或位移）时，杆的轴线将偏离铅垂位置而发生微小的弯曲，如图11.2(b)所示。

若轴向压力F较小，横向的微小扰动消除后，杆的轴线可恢复原来的铅垂平衡位置，即图11.2(a)，平衡是稳定的；若轴向压力F足够大，即使微小扰动已消除，在力F 作用下，杆轴线的弯曲挠度也仍将越来越大，如图11.2(c)所示，直至完全丧失承载能力。

在F =F cr 的临界状态下，压杆不能恢复原来的铅垂平衡位置，扰动引起的微小弯曲也不继续增大，保持微弯状态的平衡，如图11.2(b)所示，这是不稳定的平衡。

如前所述，直杆在轴向载荷作用下发生的弯曲称为屈曲，发生了屈曲就意味着构件失去稳定（失稳）。

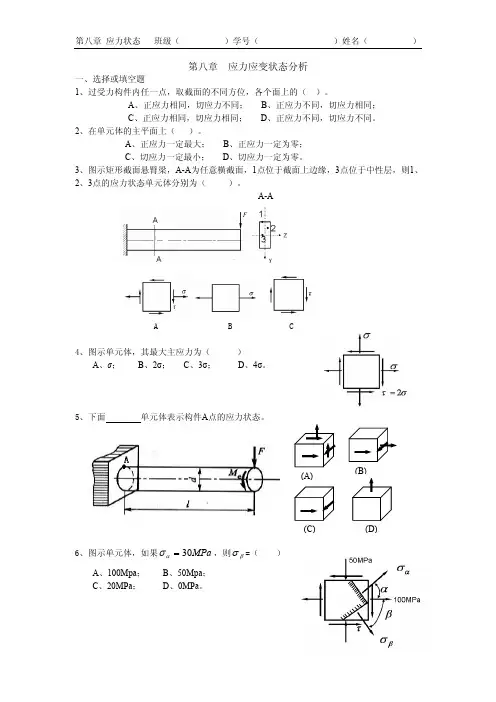
第八章 应力应变状态分析一、选择或填空题1、过受力构件内任一点，取截面的不同方位，各个面上的（ ）。

A 、正应力相同，切应力不同；B 、正应力不同，切应力相同；C 、正应力相同，切应力相同；D 、正应力不同，切应力不同。

2、在单元体的主平面上（ ）。

A 、正应力一定最大；B 、正应力一定为零；C 、切应力一定最小；D 、切应力一定为零。

3、图示矩形截面悬臂梁，A-A 为任意横截面，1点位于截面上边缘，3点位于中性层，则1、2、3点的应力状态单元体分别为（ ）。

A-AA B C4、图示单元体，其最大主应力为（ ）A 、σ；B 、2σ；C 、3σ；D 、4σ。

5、下面 单元体表示构件A 点的应力状态。

6、图示单元体，如果MPa 30=ασ，则βσ=（ ） A 、100Mpa ； B 、50Mpa ； C 、20MPa ； D 、0MPa 。

(C)7、图示单元体应力状态，沿x 方向的线应变εx 可表示为（ ）A 、Eyσ； B 、)(1y x E μσσ−；C 、)(1x y E μσσ− ；D 、Gτ。

8、图示应力圆对应于单元体( )。

9、已知单元体及应力圆如图所示，σ1所在主平面的法线方向为( )。

A 、n 1；B 、 n 2；C 、n 3；D 、n4。

二、计算题1、已知应力状态如图所示，试用解析法计算图中指定截面上的正应力和切应力。

2、试画图示应力状态的三向应力圆，并求主应力、最大正应力和最大切应力。

3、边长为20mm的钢立方块置于刚性模中，在顶面受力F=14kN作用。

已知材料的泊松比为0.3，求立方体各个面上的正应力。

4、图示矩形截面梁某截面上的弯矩和剪力分别为M=10 kN.m，Q=120 kN。

试绘出截面上1、2、3、4各点的应力状态单元体，并求其主应力。

第九章 强度理论一、选择题或填空题 1、在冬天严寒天气下，水管中的水会受冻而结冰。

根据低温下水管和冰所受力情况可知（ ）。

A 、冰先破裂而水管完好；B 、水管先破裂而冰完好；C 、冰与水管同时破裂；D 、不一定何者先破裂。

第十一章压杆稳定本章主要介绍压杆稳定的概念、压杆的临界力与临界应力的计算及适用条件，并简介中长杆的临界应力计算的经验公式和临界应力总图以及提高压杆稳定的措施。

第一节压杆稳定的概念在前面讨论受压直杆的强度问题时，认为只要满足杆受压时的强度条件，就能保证压杆的正常工作。

然而，在事实上，这个结论只适用于短粗压杆。

而细长压杆在轴向压力作用下，其破坏的形式却呈现出与强度问题截然不同的现象。

例如，一根长300mm的钢制直杆，其横截面的宽度和厚度分别为20mm和1mm，材料的抗压许用应力等于140MPa，如果按照其抗压强度计算，其抗压承载力应为2800N。

但是实际上，在压力尚不到40N时，杆件就发生了明显的弯曲变形，丧失了其在直线形状下保持平衡的能力从而导致破坏。

显然，这不属于强度性质的问题，而属于下面即将讨论的压杆稳定的范畴。

为了说明问题，取如图11—1a所示的等直细长杆，在其两端施加轴向压力F，使杆在直线形状下处于平衡，此时，如果给杆以微小的侧向干扰力，使杆发生微小的弯曲，然后撤去干扰力，则当杆承受的轴向压力数值不同时，其结果也截然不同。

当杆承受的轴向压力数值F小于某一数值F cr时，在撤去干扰力以后，杆能自动恢复到原有的直线平衡状态而保持平衡，如图11—1a、b所示，这种原有的直线平衡状态称为稳定的平衡；当杆承受的轴向压力数值F逐渐增大到（甚至超过）某一数值F cr时，即使撤去干扰力，杆仍然处于微弯形状，不能自动恢复到原有的直线平衡状态，如图11—1c、d所示，则原有的直线平衡状态为不稳定的平衡。

如果力F继续增大，则杆继续弯曲，产生显著的变形，甚至发生突然破获。

上述现象表明，在轴向压力F由小逐渐增大的过程中，压杆由稳定的平衡转变为不稳定的平衡，这种现象称为压杆丧失稳定性或者压杆失稳。

显然压杆是否失稳取决于轴向压力的数值，压杆由直线形状的稳定的平衡过渡到不稳定的平衡，具有临界的性质，此时所对应的轴向压力，称为压杆的临界压力或临界力，用Fcr表示。

第11章压杆稳定[内容提要]稳定问题是结构设计中的重要问题之一。

本章介绍了压杆稳定的概念、压杆的临界力-欧拉公式，重点讨论了压杆临界应力计算和压杆稳定的实用计算，并介绍了提高压杆稳定性的措施。

11.1 压杆稳定的概念工程中把承受轴向压力的直杆称为压杆。

前面各章中我们从强度的观点出发，认为轴向受压杆，只要其横截面上的正应力不超过材料的极限应力，就不会因其强度不足而失去承载能力。

但实践告诉我们，对于细长的杆件，在轴向压力的作用下，杆内应力并没有达到材料的极限应力，甚至还远低于材料的比例极限σP时，就会引起侧向屈曲而破坏。

杆的破坏，并非抗压强度不足，而是杆件的突然弯曲，改变了它原来的变形性质，即由压缩变形转化为压弯变形（图11-1所示），杆件此时的荷载远小于按抗压强度所确定的荷载。

我们将细长压杆所发生的这种情形称为“丧失稳定”，简称“失稳”，而把这一类性质的问题称为“稳定问题”。

所谓压杆的稳定，就是指受压杆件其平衡状态的稳定性。

为了说明平衡状态的稳定性，我们取细长的受压杆来进行研究。

图11-2(a)为一细长的理想轴心受压杆件，两端铰支且作用压力P，并使杆在微小横向干扰力作用下弯曲。

当P较小时，撤去横向干扰力以后，杆件便来回摆动最后仍恢复到原来的直线位置上保持平衡（图11-2(b)）。

因此，我们可以说杆件在轴向压力P的作用下处于稳定平衡状态。

P，杆件受到干扰后，总能回复到它原来的直线增大压力P，只要P小于某个临界值crP时，杆件虽位置上保持平衡。

但如果继续增加荷载，当轴向压力等于某个临界值，即P=cr然暂时还能在原来的位置上维持直线平衡状态，但只要给一轻微干扰，就会立即发生弯曲并停留在某一新的位置上，变成曲线形状的平衡（图11-2(c)）。

因此，我们可以认为杆件在P的作用下处在临界平衡状态，这时的压杆实质上是处于不稳定平衡状态。

P=cr(a) (b) (c)图11-1 图11-2继续增大压力P ，当轴向压力P 略大于cr P 时，由于外界不可避免地给予压杆侧向的干扰作用（例如轻微的振动，初偏心存在，材料的不均匀性，杆件制作的误差等），该杆件将立即发生弯曲，甚至折断，从而杆件失去承载能力。