下载文档原格式
第十一章压杆的稳定承受轴向压力的杆，称为压杆。
如前所述，直杆在轴向压力的作用下，发生的是沿轴向的缩短，杆的轴线仍然保持为直线，直至压力增大到由于强度不足而发生屈服或破坏。
直杆在轴向压力的作用下，是否发生屈服或破坏，由强度条件确定，这是我们已熟知的。
然而，对于一些受轴向压力作用的细长杆，在满足强度条件的情况下，却会出现弯曲变形。
杆在轴向载荷作用下发生的弯曲，称为屈曲，构件由屈曲引起的失效，称为失稳（丧失稳定性）。
本章研究细长压杆的稳定。
§11.1 稳定的概念物体的平衡存在有稳定与不稳定的问题。
物体的平衡受到外界干扰后，将会偏离平衡状态。
若在外界的微小干扰消除后，物体能恢复原来的平衡状态，则称该平衡是稳定的；若在外界的微小干扰消除后物体仍不能恢复原来的平衡状态，则称该平衡是不稳定。
如图11.1所示，小球在凹弧面中的平衡是稳定的，因为虚箭头所示的干扰（如微小的力或位移）消除后，小球会回到其原来的平衡位置；反之，小球在凸弧面上的平衡，受到干扰后将不能回复，故其平衡是不稳定的。
(a) 稳定平衡图11.1 稳定平衡与不稳定平衡上述小球是作为未完全约束的刚体讨论的。
对于受到完全约束的变形体，平衡状态也有稳定与不稳定的问题。
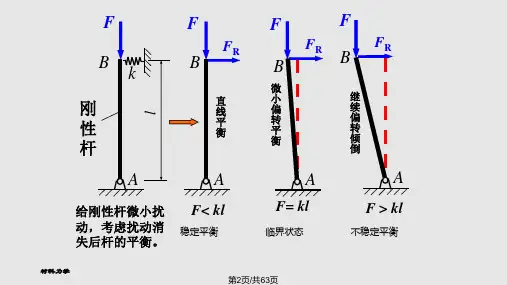
如二端铰支的受压直杆，如图11.2(a)所示。
当杆受到水平方向的微小扰动（力或位移）时，杆的轴线将偏离铅垂位置而发生微小的弯曲，如图11.2(b)所示。
若轴向压力F较小，横向的微小扰动消除后，杆的轴线可恢复原来的铅垂平衡位置，即图11.2(a)，平衡是稳定的；若轴向压力F足够大，即使微小扰动已消除，在力F 作用下，杆轴线的弯曲挠度也仍将越来越大，如图11.2(c)所示，直至完全丧失承载能力。
在F =F cr 的临界状态下，压杆不能恢复原来的铅垂平衡位置，扰动引起的微小弯曲也不继续增大，保持微弯状态的平衡，如图11.2(b)所示，这是不稳定的平衡。
如前所述，直杆在轴向载荷作用下发生的弯曲称为屈曲，发生了屈曲就意味着构件失去稳定（失稳）。
第十一章 压杆稳定
是非判断题
1 压杆失稳的主要原因是由于外界干扰力的影响。
（ ）
2 同种材料制成的压杆，其柔度愈大愈容易失稳。
（ ）
3 细长压杆受轴向压力作用，当轴向压力大于临界压力时，细长压杆不可能保持平衡。
（ ）
4 若压杆的实际应力小于欧拉公式计算的临界应力，则压杆不失稳（ ）
5 压杆的临界应力值与材料的弹性模量成正比。
（ ）
6 两根材料、长度、截面面积和约束条件都相同的压杆，则其临界力也必定相同。
（ ）
7 若细长杆的横截面面积减小，则临界压力的值必然随之增大。
（ ）
8 压杆的临界应力必然随柔度系数值的增大而减小。
（ ）
9 对于轴向受压杆来说，由于横截面上的正应力均匀分布，因此不必考虑横截面的合理形状问题。
（ ）
填空题
10 在一般情况下，稳定安全系数比强度安全系数要大，这是因为实际压杆总是不可避免地存在 以及 等不利因素的影响。
11 按临界应力总图，1λλ≥的压杆称为 ，其临界应力计算公式为 ；1
2λλλ≤≤的压杆称为 ，其临界应力计算公式为 ；2λλ≤的压杆称为 ，其临界应力计算公式为 。
12 理想压杆的条件是① ；② ；③ 。
13 压杆有局部削弱时，因局部削弱对杆件整体变形的影响 ；所以在计算临界压力时，都采
用 的横截面面积A 和惯性矩I 。
14 图示两端铰支压杆的截面为矩形，当其失稳时临界压力F cr = ，挠曲线位于 平面
内。
z 题15图
15 图示桁架，AB 和BC 为两根细长杆，若EI 1＞EI 2，则结构的临界载荷F cr = 。
16 对于不同柔度的塑性材料压杆，其最大临界应力将不超过材料的 。
17 提高压杆稳定性的措施有 ， ，以及 和 。
18 细长杆的临界力与材料的 有关，为提高低碳钢压杆的稳定性，改用高强度钢不经济，
原因时 。
19 按图示钢结构（a ）变换成（b ）的形式，若两种情形下CD 为细长杆，结构承载能力将 。
B
P
A C
B D
P
(a)
(b) 20 图示材料相同，直径相等的细长杆中， 杆能承受压力最大； 杆能承受的压力最小。
F
（a (b) (c)
选择题
21 在稳定性计算中，若用欧拉公式算得压杆的临界压力为F cr ，而实际压杆属于中柔度杆，则（ ）。
（A ）并不影响压杆的临界压力值；
（B ）实际的临界压力大于F cr ，是偏于安全的；
（C ）实际的临界压力大于F cr ，是偏于不安全的；
（D ）实际的临界压力小于F cr ，是偏于不安全的；
22 方形截面压杆，2:1:=h b ；如果将b 改为h 后仍为细长杆，临界力cr P 是原来的多少倍？( )
（A ）16倍； （B ）8倍； （C ）4倍； （D ）2倍。
b
23 在横截面积等其他条件均相同的条件下，压杆采用图（ ）所示的截面形状，其稳定性最好。
F
(A) (B) (C) (D)
题23图 题24图
24 图示边长为1032⨯=a mm 的正方形截面大柔度杆，承受轴向压力F=4π2
KN ，弹性模量E=100GPa 。
则该杆的工作安全系数为（ ）。
（A ）1=w n ； （B ）2=w n ； （C ）3=w n ； （D ）4=w n 。
25 图示结构二杆材料和截面形状与尺寸相同，均为细长杆，若在平面内失稳而破坏，则结构的临界
载荷，沿（ ）方位作用时，其值最小；沿（ ）方位作用时，其值最大。
（A ）00=θ； （B ）0
90=θ；
（B ）030=θ； （D ）使二杆同时进入临界状态的θ值。
B
A 300 C
计算题
26 图示简单托架，其撑杆AB 为圆截面木杆，若架上受集度为q=24KN/m 的均布荷载作用，AB 两端为铰支，木材的E=10GPa ，p σ=20MPa ，规定的稳定安全系数st n =3，试校核AB 杆的稳定性。
27 一端固定一端铰支压杆的长度L=1.5m ，材料为A3钢，其弹性模量E=205GPa ，
p σ=200MPa ，S σ=240MPa 。
已知截面面积A=800mm 2
，若截面的形状分别为实心圆形和D d =0.8的空心圆管，试分别计算各杆的临界压力。
若用经验公式，A3钢计算临界应力的直线公式为λσ12.1304-=cr （单位Mpa ）。
28 图示结构，1、2两杆长度、面积均相同，1杆为圆截面，2杆为圆环截面。
A=900mm 2，材料的E=200GPa ，p λ=100，s λ=61.4，临界应力经验公式为λσ12.1304-=cr (MPa)，求两杆的临界力及结构失稳时的载荷F 。
取6.0/22=D d 。
