七年级数学上册第三章代数式3.2代数式第4课时探索规律同步训练新版冀教版201808071174

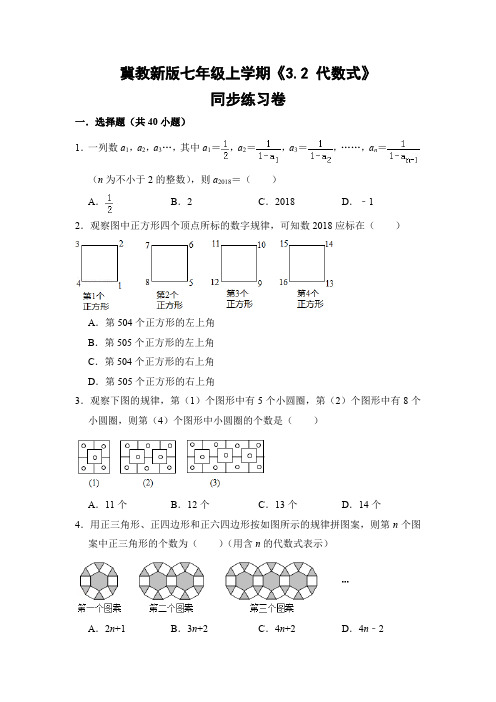
冀教新版七年级上学期《3.2 代数式》同步练习卷一．选择题（共40小题）1．一列数a1，a2，a3…，其中a1＝，a2＝，a3＝，……，a n＝（n为不小于2的整数），则a2018＝（）A．B．2C．2018D．﹣12．观察图中正方形四个顶点所标的数字规律，可知数2018应标在（）A．第504个正方形的左上角B．第505个正方形的左上角C．第504个正方形的右上角D．第505个正方形的右上角3．观察下图的规律，第（1）个图形中有5个小圆圈，第（2）个图形中有8个小圆圈，则第（4）个图形中小圆圈的个数是（）A．11个B．12个C．13个D．14个4．用正三角形、正四边形和正六四边形按如图所示的规律拼图案，则第n个图案中正三角形的个数为（）（用含n的代数式表示）A．2n+1B．3n+2C．4n+2D．4n﹣25．把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为（）A．12B．14C．16D．186．下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片，第③个图中有7张黑色正方形纸片，…，按此规律排列下去第⑥个图中黑色正方形纸片的张数为（）A．11B．13C．15D．177．观察图中的“品”字形中个数之间的规律，根据观察到的规律得出a的值为（）A．75B．89C．103D．1398．如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M与m、n的关系是（）A．M＝mn B．M＝m（n+1）C．M＝mn+1D．M＝n（m+1）9．如图，是一组按照某种规律摆放而成的图案，第1个图有1个三角形，第二个图有4个三角形，第三个图有8个三角形，第四个图有12个三角形，则图5中三角形的个数是（）A．8B．12C．16D．1710．如图：●和〇两种圆按某种规则排列，则前2017个圆中有〇（）个〇●〇●●〇●●●〇●〇●●〇●●●〇●〇●●〇●●●…A．671B．672C．673D．67411．如图是一组有规律的图案，第1个图案由1个▲组成，第2个图案由4个▲组成，第3个图案由7个▲组成，第4个图案由10个▲组成，…，则第7个图案▲的个数为（）A．16B．17C．18D．1912．一个由小菱形组成的装饰链，断去了一部分，剩下部分如图所示，则断去部分的小菱形的个数可能是（）A．2016个B．2015个C．2014个D．2013个13．将全体自然数按下面的方式进行排列：按照这样的排列规律，2014应位于（）A．位B．位C．位D．位14．下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有9个，第（2）个图形中面积为1的正方形有14个，…，按此规律．则第（10）个图形中面积为1的正方形的个数为（）A．72B．64C．54D．5015．将一些完全相同的梅花按如图所示的规律摆放，第1个图形有5朵梅花，第2个图形有8朵梅花，第3个图形有13朵梅花，…，按此规律，则第11个图形中共有梅花的朵数是（）A．121B．125C．144D．14816．已知一列数：1、﹣2、3、﹣4、5、﹣6、……，将这列数排成下列形式：按照上述规律排列下去，第10行数的第1个数是（）A．﹣46B．﹣36C．37D．4517．我国2017年GDP位于世界第二，教育经费投入是当年GDP的4%．若2017年GDP的总值为n亿元，则当年教育经费投入为（）亿元．A．4%n B．（1+4%）n C．（1﹣4%）n D．4%+n18．某企业今年1月份产值为x万元，2月份比1月份增加了10%，3月份比2月份减少了20%，则3月份的产值是（）万元．A．（1+10%）（1﹣20%）x B．（1+10%+20%）xC．（x+10%）（x﹣20%）D．（1+10%﹣20%）x19．七年级1班有女生m人，女生占全班人数的40%，则全班人数是（）A．B．40%m C．D．（1﹣40%）m 20．小强购买绿、橙两种颜色的珠子串成一条手链，已知绿色珠子a个，每个2元，橙色珠子b个，每个5元，那么小强购买珠子共需花费（）A．（2a+5b）元B．（5a+2b）元C．2（a+5b）元D．5（2a+b）元21．苹果的单价为a元/千克，香蕉的单价为b元/千克，买2千克苹果和3千克香蕉共需（）A．（a+b）元B．（3a+2b）元C．（2a+3b）元D．5（a+b）元22．某工程甲独做12天能完成一半，乙独做需18天完成．现在由甲乙合做了x 天，完成了这项工程的（）A．+B．+C．+D．+23．一辆汽车行驶akm后，又以vkm/h的速度行驶了th，则这辆汽车行驶的全部路程是（）km．A．vt B．a+vt C．a﹣vt D．2a﹣vt24．一艘船顺流航行m千米用了n小时，如果逆流航速是顺流航速的，那么这艘船逆流航行s千米需要用（）小时．A．B．C．D．25．甲每小时走a千米，乙每小时走b千米，两人同时同地出发反向行走，2小时后，他们之间的距离为（）千米．A．2a+2b B．2a+b C．2a﹣2b D．a+b26．一辆汽车a秒行驶米，则它2分钟行驶（）A．米B．米C．米D．米27．已知轮船在静水中的速度是a千米/小时，水流的速度是5千米/小时，某轮船顺水航行3小时，则轮船航行（）千米．A．3a B．3（a+5）C．3a+5D．a+1528．今年，我校成功举办了“经典诵读”比赛，其中参加比赛的男同学有a人，女同学比男同学的少24人，则参加“经典诵读”比赛的学生一共有（）A．（﹣24）人B．（a﹣24）人C．（a+24）人D．（﹣24）人29．某商品标价x元，进价为400元，在商场开展的促销活动中，该商品按8折销售获利（）A．（8x﹣400）元B．（400×8﹣x）元C．（0.8x﹣400）元D．（400×0.8﹣x）元30．苹果每千克m元，买10千克以上8.5折优惠（即按原价的85%出售），买30千克应付（）A．30×（1+85%）m元B．30×（1﹣85%）m元C．30×85%m元D．30m元31．今年苹果的价格比去年便宜了20%，已知去年苹果的价格是每千克a元，则今年每千克的价格是（）A．元B．（1﹣20%）a元C．20%a元D．元32．甲乙两超市为了促销一种定价相同的商品，甲超市连续两次降价5%，乙超市一次性降价10%，在哪个超市购买这种商品合算？下列选项中正确的是（）A．甲超市B．乙超市C．两个超市一样D．与商品的价格有关33．七年级同学进行体能测试，一班有a个学生，平均成绩m分，二班有b个学生，平均成绩n分，则一、二班的平均成绩为多少分（）A．B．C．D．34．某商品进价为a元，商店将其价格提高30%作零售价销售，在销售旺季过后，商店又以8折（即售价的80%）优惠开展促销活动，这时一件商品的售价为（）A．a元B．0.8a元C．0.92a元D．1.04a元35．每件上衣的原价为a元，降价10%后的售价是（）A．10%a B．（1﹣10%）a C．（1+10%）a D．（1+90%）a 36．如图，一个窗户的上部是由4个扇形组成的半圆，下部是由4个边长相同的小正方形组成的长方形，则这个窗户的外框总长为（）A．6a+πa B．12a C．15a+πa D．6a37．小明父亲拟用不锈钢制造一个上部是一个长方形、下部是一个正方形的窗户，相关数据（单位米）如图所示，那么制造这个窗户所需不锈钢的总长是（）A．（4a+2b）米B．（5a+2b）米C．（6a+2b）米D．（a2+ab）米38．有长为l的篱笆，利用他和房屋的一面墙围成如图形状的长方形园子，园子的宽为t，则所围成的园子面积为（）A．（l﹣2t）t B．（l﹣t）t C．（﹣t）t D．（l﹣）t 39．如图，正方形的边长为a，圆的直径是d，用字母表示图中阴影部分的面积为（）A．a2﹣2dπB．a2﹣d2πC．D．40．如图是一块长为a，宽为b（a＞b）的长方形空地，要将阴影部分绿化，则阴影面积是（）A．a2b2B．ab﹣πa2C．D．冀教新版七年级上学期《3.2 代数式》2018年同步练习卷参考答案与试题解析一．选择题（共40小题）1．一列数a1，a2，a3…，其中a1＝，a2＝，a3＝，……，a n＝（n为不小于2的整数），则a2018＝（）A．B．2C．2018D．﹣1【分析】把a1，a2，a3代入代数式计算，找出规律，根据规律计算．【解答】解：a1＝，a2＝＝＝2，a3＝＝＝﹣1，a4＝＝＝……，2018÷3＝672……2，∴a2018＝2，故选：B．【点评】本题考查的是规律型：数字的变化类问题，正确找出数字的变化规律是解题的关键．2．观察图中正方形四个顶点所标的数字规律，可知数2018应标在（）A．第504个正方形的左上角B．第505个正方形的左上角C．第504个正方形的右上角D．第505个正方形的右上角【分析】观察图形得到一个正方形从右下角开始按逆时针方向标四个数，而2018＝4×504+2，则可判断数2018应标在第505个正方形的右上角．【解答】解：∵2018＝4×504+2，∴数2018应标在第505个正方形的右上角．故选：D．【点评】本题考查了规律型：图形的变化类：通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．3．观察下图的规律，第（1）个图形中有5个小圆圈，第（2）个图形中有8个小圆圈，则第（4）个图形中小圆圈的个数是（）A．11个B．12个C．13个D．14个【分析】根据图形，可以发现图形中小圆圈的个数的变化规律，从而可以得到第（4）个图形中小圆圈的个数．【解答】解：由图可得，第（1）个图形中小圆圈的个数是：2+3×1＝5，第（2）个图形中小圆圈的个数是：2+3×2＝8，第（3）个图形中小圆圈的个数是：2+3×3＝11，故第（4）个图形中小圆圈的个数是：2+3×4＝14，故选：D．【点评】本题考查图形的变化类，解答本题的关键是明确题意，利用数形结合的思想解答．4．用正三角形、正四边形和正六四边形按如图所示的规律拼图案，则第n个图案中正三角形的个数为（）（用含n的代数式表示）A．2n+1B．3n+2C．4n+2D．4n﹣2【分析】设第n个图案中正三角形的个数为a n，观察图案找出a1，a2，a3，…，的值，根据数的变化，即可找出a n＝6+4（n﹣1）＝4n+2，此题得解．【解答】解：设第n个图案中正三角形的个数为a n．∵a1＝6，a2＝6+4＝10，a3＝6+4+4＝14，…，∴a n＝6+4（n﹣1）＝4n+2．故选：C．【点评】本题考查了规律型：图形的变化类以及列代数式，根据图形的变化找出a n＝4n+2是解题的关键．5．把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为（）A．12B．14C．16D．18【分析】根据第①个图案中三角形个数4＝2+2×1，第②个图案中三角形个数6＝2+2×2，第③个图案中三角形个数8＝2+2×3可得第④个图形中三角形的个数为2+2×7．【解答】解：∵第①个图案中三角形个数4＝2+2×1，第②个图案中三角形个数6＝2+2×2，第③个图案中三角形个数8＝2+2×3，……∴第⑦个图案中三角形的个数为2+2×7＝16，故选：C．【点评】本题主要考查图形的变化规律，根据题意得出第n个图形中三角形的数量个数是2n+2．6．下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片，第③个图中有7张黑色正方形纸片，…，按此规律排列下去第⑥个图中黑色正方形纸片的张数为（）A．11B．13C．15D．17【分析】仔细观察图形知道第一个图形有3个正方形，第二个有5＝3+2×1个，第三个图形有7＝3+2×2个，由此得到规律求得第⑥个图形中正方形的个数即可．【解答】解：观察图形知：第一个图形有3个正方形，第二个有5＝3+2×1个，第三个图形有7＝3+2×2个，…故第⑥个图形有3+2×5＝13（个），故选：B．【点评】此题主要考查了图形的变化规律，是根据图形进行数字猜想的问题，关键是通过归纳与总结，得到其中的规律，然后利用规律解决一般问题．7．观察图中的“品”字形中个数之间的规律，根据观察到的规律得出a的值为（）A．75B．89C．103D．139【分析】由1、3、5、…为连续的奇数可知，11所在“品”字形为第6个图形，由左下的数字为2、4、8、…可得出b＝26＝64，再由右下数字为上面数字加左下数字，即可求出a值．【解答】解：∵“品”字形中上面的数字为连续的奇数，左下的数字为2、4、8、…，∴11所在“品”字形为第6个图形，∴b＝26＝64．又∵1+2＝3，3+4＝7，5+8＝13，…，∴a＝11+b＝75．故选：A．【点评】本题考查了规律型中数字的变化类，根据“品”字形中数字的变化，找出变化规律是解题的关键．8．如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M与m、n的关系是（）A．M＝mn B．M＝m（n+1）C．M＝mn+1D．M＝n（m+1）【分析】根据给定图形中三个数之间的关系找出规律“右下圆圈内的数＝上方圆圈内的数×（左下圆圈内的数+1）”，由此即可得出结论．【解答】解：∵1×（2+1）＝3，3×（4+1）＝15，5×（6+1）＝35，∴右下圆圈内的数＝上方圆圈内的数×（左下圆圈内的数+1），∴M＝m（n+1）．故选：B．【点评】本题考查了规律型中数字的变化类，根据给定图形中三个数之间的关系找出变化规律“右下圆圈内的数＝上方圆圈内的数×（左下圆圈内的数+1）”是解题的关键．9．如图，是一组按照某种规律摆放而成的图案，第1个图有1个三角形，第二个图有4个三角形，第三个图有8个三角形，第四个图有12个三角形，则图5中三角形的个数是（）A．8B．12C．16D．17【分析】对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，进而得出即可．【解答】解：由图可知：第一个图案有三角形1个．第二图案有三角形1+3＝4个．第三个图案有三角形1+3+4＝8个，第四个图案有三角形1+3+4+4＝12第五个图案有三角形1+3+4+4+4＝16故选：C．【点评】此题主要考查了图形的变化规律，注意由特殊到一般的分析方法．这类题型在中考中经常出现．10．如图：●和〇两种圆按某种规则排列，则前2017个圆中有〇（）个〇●〇●●〇●●●〇●〇●●〇●●●〇●〇●●〇●●●…A．671B．672C．673D．674【分析】根据图形可以得到如下规律：〇●〇●●〇●●●为一组，以后反复如此．首先求出2017中有多少组，再由余数来决定最后一个圆是什么颜色．【解答】解：由题意可知，前9个圆为本图规律，后边就按这个规律排列．2017÷9＝224余1，可知2017个圆为空心圆，故前2017个圆中，有224×3＝672+1＝673个空心圆．故选：C．【点评】本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．注意多看看，找准规律再计算．11．如图是一组有规律的图案，第1个图案由1个▲组成，第2个图案由4个▲组成，第3个图案由7个▲组成，第4个图案由10个▲组成，…，则第7个图案▲的个数为（）A．16B．17C．18D．19【分析】仔细观察图形可知：第一个图形有1个三角形；第二个图形有3×2﹣3+1＝4个三角形；第三个图形有3×3﹣3+1＝7个三角形；第四个图形有3×4﹣3+1＝10个三角形；…第n个图形有3n﹣3+1＝3n﹣2个三角形；进一步代入求得答案即可．【解答】解：观察发现：第一个图形有1个三角形；第二个图形有3×2﹣3+1＝4个三角形；第三个图形有3×3﹣3+1＝7个三角形；第四个图形有3×4﹣3+1＝10个三角形；…第n个图形有3n﹣3+1＝3n﹣2个三角形；则第7个图案中▲的个数为3×7﹣2＝19．故选：D．【点评】此题考查图形的变化规律，从简单情形入手，找到一般规律，利用规律，解决问题．12．一个由小菱形组成的装饰链，断去了一部分，剩下部分如图所示，则断去部分的小菱形的个数可能是（）A．2016个B．2015个C．2014个D．2013个【分析】将上、下、左三个小菱形当成一个整体，根据图形即可得出完整的装饰链中小菱形的个数为3n+1，用其减去图中小菱形的个数对照四个选项即可得出结论．【解答】解：将上、下、左三个小菱形当成一个整体，则完整的装饰链中小菱形的个数为3n+1，断去部分的小菱形的个数为3n+1﹣10﹣7＝3n﹣16．∵2016+16＝677×3+1，2015+16＝677×3，2014+16＝676×3+2，2013+16＝676×3+1，∴断去部分的小菱形的个数可能是2015．故选：B．【点评】本题考查了规律型中图形的变化类，根据图形的变化找出变化规律是解题的关键．13．将全体自然数按下面的方式进行排列：按照这样的排列规律，2014应位于（）A．位B．位C．位D．位【分析】观察图形不难发现，每4个数为一个循环组依次循环，因为2014是第2015个数，所以用2015除以4，再根据商和余数的情况确定2014所在的位置即可．【解答】解：由图可知，每4个数为一个循环组依次循环，∵2014是第2015个数，∴2015÷4＝503余3，∴2014应位于第504循环组的第3个数，在位．故选：C．【点评】本题是对数字变化规律的考查，观察出每4个数为一个循环组依次循环是解题的关键，要注意2014是第2015个数．14．下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有9个，第（2）个图形中面积为1的正方形有14个，…，按此规律．则第（10）个图形中面积为1的正方形的个数为（）A．72B．64C．54D．50【分析】由第1个图形有9个边长为1的小正方形，第2个图形有9+5＝14个边长为1的小正方形，第3个图形有9+5×2＝19个边长为1的小正方形，…由此得出第n个图形有9+5×（n﹣1）＝5n+4个边长为1的小正方形，由此求得答案即可．【解答】解：第1个图形边长为1的小正方形有9个，第2个图形边长为1的小正方形有9+5＝14个，第3个图形边长为1的小正方形有9+5×2＝19个，…第n个图形边长为1的小正方形有9+5×（n﹣1）＝5n+4个，所以第10个图形中边长为1的小正方形的个数为5×10+4＝54个．故选：C．【点评】此题考查图形的变化规律，找出图形与数字之间的运算规律，利用规律解决问题．15．将一些完全相同的梅花按如图所示的规律摆放，第1个图形有5朵梅花，第2个图形有8朵梅花，第3个图形有13朵梅花，…，按此规律，则第11个图形中共有梅花的朵数是（）A．121B．125C．144D．148【分析】由题意可知：第1个图形有1+45朵梅花，第2个图形有1+2+1+4＝8朵梅花，第3个图形有1+2+3+2+1+4＝13朵梅花，…由此得出第n个图形中共有梅花的朵数是1+2+3+4+…+n+n﹣1+…+4+3+2+1+4＝n2+4，由此代入求得答案即可．【解答】解：∵第1个图形有1+4＝5朵梅花，第2个图形有1+2+1+4＝8朵梅花，第3个图形有1+2+3+2+1+4＝13朵梅花，…∴第n个图形中共有梅花的朵数是1+2+3+4+…+n+n﹣1+…+4+3+2+1+4＝n2+4，则第11个图形中共有梅花的朵数是112+4＝125．故选：B．【点评】此题考查图形的变化规律，找出图形之间的运算规律，利用规律解决问题．16．已知一列数：1、﹣2、3、﹣4、5、﹣6、……，将这列数排成下列形式：按照上述规律排列下去，第10行数的第1个数是（）A．﹣46B．﹣36C．37D．45【分析】观察排列规律得到第1行有1个数，第2行有2个数，第3行有1个数，…，第9行有9个数，则可计算出前9行的数的个数45，而数字的序号为偶数时，数字为负数，于是可判断第10行数的第1个数为﹣46．故选A．【解答】解：第1行有1个数，第2行有2个数，第3行有1个数，…，第9行有9个数，所以前9行的数的个数为1+2+3+…+9＝45，而数字的序号为奇数时，数字为正数，数字的序号为偶数时，数字为负数，所以第10行数的第1个数为﹣46．故选：A．【点评】本题考查了规律型：数字的变化类：认真观察、仔细思考，利用数字与序号数的关系解决这类问题．17．我国2017年GDP位于世界第二，教育经费投入是当年GDP的4%．若2017年GDP的总值为n亿元，则当年教育经费投入为（）亿元．A．4%n B．（1+4%）n C．（1﹣4%）n D．4%+n【分析】根据2017年GDP的总值为n亿元，教育经费投入是当年GDP的4%，即可得出2017年教育经费投入．【解答】解：因为2017年GDP的总值为n亿元，教育经费投入应占当年GDP的4%，所以2017年教育经费投入可表示为4%n亿元．故选：A．【点评】此题主要考查了列代数式，解此题的关键是根据已知条件找出数量关系，列出代数式．18．某企业今年1月份产值为x万元，2月份比1月份增加了10%，3月份比2月份减少了20%，则3月份的产值是（）万元．A．（1+10%）（1﹣20%）x B．（1+10%+20%）xC．（x+10%）（x﹣20%）D．（1+10%﹣20%）x【分析】根据题意可以先列出2月份的产量为（1+10%）x，再根据题意可列三月份的产量．【解答】解：根据题意可得2月份产量为x（1+10%）万元∵3月份比2月份减少了20%∴3月份的产量为（1+10%）（1﹣20%）x故选：A．【点评】本题考查了列代数式，能根据题意正确列出代数式是本题关键19．七年级1班有女生m人，女生占全班人数的40%，则全班人数是（）A．B．40%m C．D．（1﹣40%）m 【分析】根据全班人数＝女生人数÷女生所占百分比即可列式求解．【解答】解：∵七年级1班有女生m人，女生占全班人数的40%，∴全班人数是．故选：A．【点评】本题考查了列代数式，列代数式时，要注意语句中的关键字，根据题意找出数据之间的联系，并准确的用代数式表示出来．20．小强购买绿、橙两种颜色的珠子串成一条手链，已知绿色珠子a个，每个2元，橙色珠子b个，每个5元，那么小强购买珠子共需花费（）A．（2a+5b）元B．（5a+2b）元C．2（a+5b）元D．5（2a+b）元【分析】直接利用两种颜色的珠子的价格进而求出手链的价格．【解答】解：∵绿色珠子每个2元，橙色珠子每个5元，∴小强购买珠子共需花费（2a+5b）元，故选：A．【点评】此题主要考查了列代数式，正确得出各种颜色珠子的数量是解题关键．21．苹果的单价为a元/千克，香蕉的单价为b元/千克，买2千克苹果和3千克香蕉共需（）A．（a+b）元B．（3a+2b）元C．（2a+3b）元D．5（a+b）元【分析】根据题意列出代数式即可．【解答】解：根据题意得：买2千克苹果和3千克香蕉共需（2a+3b）元，故选：C．【点评】此题考查了列代数式，弄清题意是解本题的关键．22．某工程甲独做12天能完成一半，乙独做需18天完成．现在由甲乙合做了x 天，完成了这项工程的（）A．+B．+C．+D．+【分析】利用工作总量＝工作效率×工作时间，即可得出结论．【解答】解：+＝+．故选：B．【点评】本题考查了列代数式，根据数量关系，列出代数式是解题的关键．23．一辆汽车行驶akm后，又以vkm/h的速度行驶了th，则这辆汽车行驶的全部路程是（）km．A．vt B．a+vt C．a﹣vt D．2a﹣vt【分析】根据“全部路程＝之前行驶路程+后来的速度×行驶时间”可得．【解答】解：根据题意知这辆汽车行驶的全部路程是（a+vt）km，故选：B．【点评】本题主要考查列代数式，关键知道路程＝速度×时间，从而可列出代数式．24．一艘船顺流航行m千米用了n小时，如果逆流航速是顺流航速的，那么这艘船逆流航行s千米需要用（）小时．A．B．C．D．【分析】根据题意表示出顺流速度，进而表示出逆流速度，即可得到这艘船逆流航行s千米所用的时间．【解答】解：根据题意得：顺流速度为km/h，逆流速度km/h，则这艘船逆流航行s千米需要用小时；故选：B．【点评】此题考查了根据题意列代数式的能力，列出正确的代数式是解本题的关键．25．甲每小时走a千米，乙每小时走b千米，两人同时同地出发反向行走，2小时后，他们之间的距离为（）千米．A．2a+2b B．2a+b C．2a﹣2b D．a+b【分析】根据题意，可以用相应的代数式表示出t小时后他们之间的距离．【解答】解：由题意可得，2小时后他们之间的距离是：（a+b）×2＝（2a+2b）千米，故选：A．【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．26．一辆汽车a秒行驶米，则它2分钟行驶（）A．米B．米C．米D．米【分析】先统一单位，2分钟＝120秒，再根据求出速度．【解答】解：由题意可知：速度为：÷a＝米/秒，所以2分钟行驶了：×120＝，故选：C．【点评】本题考查列代数式，属于基础题型，注意单位不统一时需要进行统一单位后才能进行计算．27．已知轮船在静水中的速度是a千米/小时，水流的速度是5千米/小时，某轮船顺水航行3小时，则轮船航行（）千米．A．3a B．3（a+5）C．3a+5D．a+15【分析】根据路程等于速度乘以时间的等量关系即可求出答案．【解答】解：根据题意知轮船顺水航行的速度为（a+5）千米/小时，所以轮船顺水航行3小时的路程为3（a+5）千米，故选：B．【点评】此题考查列代数式，掌握静水速度、水流速度、顺水速度、逆水速度之间的关系是解决问题的关键．28．今年，我校成功举办了“经典诵读”比赛，其中参加比赛的男同学有a人，女同学比男同学的少24人，则参加“经典诵读”比赛的学生一共有（）A．（﹣24）人B．（a﹣24）人C．（a+24）人D．（﹣24）人【分析】先表示女同学的人数：女同学比男同学的少24人，即：a﹣24，相加可得结论．【解答】解：女同学人数：a﹣24，所以一共有学生：a+a﹣24＝a﹣24，故选：D．【点评】本题考查了列代数式，解题关键是要读懂题目的意思，根据题目给出的条件列出代数式．29．某商品标价x元，进价为400元，在商场开展的促销活动中，该商品按8折销售获利（）A．（8x﹣400）元B．（400×8﹣x）元C．（0.8x﹣400）元D．（400×0.8﹣x）元【分析】根据题意，可以用代数式表示出该商品按8折销售所获利润，本题得以解决．【解答】解：由题意可得，该商品按8折销售获利为：（0.8x﹣400）元，故选：C．【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．30．苹果每千克m元，买10千克以上8.5折优惠（即按原价的85%出售），买30千克应付（）A．30×（1+85%）m元B．30×（1﹣85%）m元C．30×85%m元D．30m元【分析】根据苹果每千克m元，买10千克以上8.5折优惠，可以求得买30千克应付的钱数．【解答】解：∵买10千克以上8.5折优惠，∴买30千克应付30×85%m元，故选：C．【点评】本题考查了列代数式，解答此题的关键是根据题意求出优惠后每千克的钱数．31．今年苹果的价格比去年便宜了20%，已知去年苹果的价格是每千克a元，则今年每千克的价格是（）A．元B．（1﹣20%）a元C．20%a元D．元【分析】根据今年苹果的价格比去年便宜了20%，可得今年的价格＝去年的价格×（1﹣20%），将去年苹果的价格每千克a元代入即可求出今年每千克的价格．【解答】解：由题意可得，今年每千克的价格是（1﹣20%）a元．故选：B．【点评】本题考查了列代数式，列代数式的关键是正确理解文字语言中的关键词，找到其中的数量关系．注意增长率或降低率的基数．32．甲乙两超市为了促销一种定价相同的商品，甲超市连续两次降价5%，乙超市一次性降价10%，在哪个超市购买这种商品合算？下列选项中正确的是（）A．甲超市B．乙超市C．两个超市一样D．与商品的价格有关【分析】根据题意，分别列出降价后在甲乙两个商场的购物价格，问题即可解决．【解答】解：设商品的定价为λ，则在甲超市购买这种商品价格为：＝；在乙超市购买这种商品的价格为：＝，∴在乙超市购买这种商品合算．故选：B．【点评】该题考查了列代数式在现实生活中的应用问题；解题的关键是深刻把握题意，正确列出代数式，准确求解运算．33．七年级同学进行体能测试，一班有a个学生，平均成绩m分，二班有b个学生，平均成绩n分，则一、二班的平均成绩为多少分（）A．B．C．D．【分析】先求出一班、二班的总成绩，用总成绩÷总人数，即可求解．【解答】解：一班二班的总成绩为：ma+nb，总人数为：a+b，则平均分＝＝．故选：C．【点评】本题考查了列代数的知识，解答本题的关键是读懂题意，求出总成绩和总人数．34．某商品进价为a元，商店将其价格提高30%作零售价销售，在销售旺季过后，商店又以8折（即售价的80%）优惠开展促销活动，这时一件商品的售价为（）A．a元B．0.8a元C．0.92a元D．1.04a元【分析】此题的等量关系：进价×（1+提高率）×打折数＝售价，代入计算即可．【解答】解：根据题意商品的售价是：a（1+30%）×80%＝1.04a元．故选：D．【点评】考查了列代数式的知识，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的数量关系进行解题．有关销售问题中的提高30%，8折优惠等名词要理解透彻，正确应用．35．每件上衣的原价为a元，降价10%后的售价是（）A．10%a B．（1﹣10%）a C．（1+10%）a D．（1+90%）a 【分析】原来的价格×（1﹣降低的百分率）＝降价后的价格，据此即可列出代数式．【解答】解：原价为a元，降价10%后的售价是：a（1﹣10%）．故选B．。

第三章代数式3.2 代数式第4课时探索规律教学目标1. 使学生会用代数式表示简单的数量关系，验证所探索的规律.2. 通过从特殊事例中抽象概括一般规律的过程，学会从不同角度分析和解决问题，学会转化思想和归纳思想.教学重难点重点：用代数式表示规律.难点：厘清数量关系，用运算验证规律.教学过程导入新课如图，这是一个由1～120的连续整数排成的“数阵”.如果用方框围住9个数，那么这9个数的和随方框位置的变化而变化.你发现这些数字有什么规律吗？学生独立思考每行每列数字之间的规律.探究新知探究一：1.如果设方框左上角的数为a，用含a的代数式表示这9个数的和.思考：（1）方框内每行的三个数之和，和中间的数有什么关系？（2）怎样表示这九个数的和比较简单？2.方框内9个数的和，与中间的数15有什么关系？3.如果方框下移一行，中间数变为21，此时9个数的和是多少？4.根据上述规律，你能直接写出中间数为m时这9个数的和吗？学生思考交流，教师点拨.答案：1.（1）三个数的和是中间数的三倍；（2）三行数的和依次为3（a+1），3（a+7），3（a+13），故九个数的和为9（a+7）.2.九个数的和为135，为15的9倍.教学反思3.21的9倍.4.这九个数的和为9m .探究二：图1是由点组成的n 行n 列的方阵，图2是由每条边上n 个点围成的空心方阵.图1 图2 1. 图1中方阵的总点数为多少？ 2. 图2中方阵的总点数是多少？你还有其他的计算方法吗？让学生分组讨论，自主探究，然后教师多媒体演示图2中总点数不同的计算方法. 答案：1. n 22.可以是22(2)n n --，4（n -1），2n +2（n −2），4n −4. 课堂练习1.一组按规律排列的数：137132149162536，，，，，… ，第7个数是________；第n 个数是_____________. 2.观察下列等式：1×3＝221-；2×4＝231-； 3×5＝241-；（ ）×（ 6）＝（ ）2−（ ）；填写第4个等式，第n 个等式为 .3.如图，第一排有 1 个三角形；第二排有 3 个三角形；第三排有 5 个三角形；第四排有 个三角形；第n 排有 个三角形；4.如图，按下列格式用火柴棒搭建正方形.1个正方形用4根火柴棒；2个正方形用 火柴棒；3个正方形用___火柴棒；10个正方形用 火柴棒；n 个正方形用 火柴棒 . 参考答案1. 4364 n 2−（n−1）（n+1）2 2. 4 6 5 1 n （n +2）＝(n +1)2 −1教学反思3. 7 （2n-1）教学反思4. 7根10根31根（3n+1）根课堂小结用代数式表示规律：1.用代数式表示数的变化规律；2.用代数式表示图形的变化规律.布置作业教材第108页习题A组第1，2，3题.板书设计第三章代数式3.2 代数式第4课时探索规律探究一：探究二：。

3.2 代数式1．x 表示一个两位数，y 表示一个两位数，把x 放在y 的左面，末位再添上1得到一个五位数，这个五位数等于（ ）.A ．1000x +y +1B ．xy 1C ．1000x +10y +1D ．x +y +12.已知三个连续奇数，最大的一个是m ，用代数式表示其他两个数应为（ ）. A ．m -1,m -2 B ． m -2,m -3 C ．m -3,m -4 D ．m -2,m -43.用代数式表示a 与-b 的差的2倍是( ).A ．a - 2(- b )B ．a +2(- b )C ．2(a - b )D ．2(a +b ) 4.下列语句不正确的是（ ）.A ．0是代数式B ．a 是代数式C ．x 的3倍与y 的14的差表示为134x y - D ．s =πr 2是代数式 5.下列各式：2m ，0，-2n ，b a ，221,,x x y a b ab x+-+=中，代数式有（ ） A ．4个 B ．5个 C ．6个 D ．7个6.某班共有x 个学生，其中女生占45%，那么男生人数是( )A ．45%xB ．(1-45%)xC ．45%xD ．145%x - 7.已知某数比a 大30%，则某数是（ ）.A ．30%aB ．(1-30%)aC ． (1+30%) aD ．a +30%8.若a 增加x %后得到b ，那么b =( ).A ．ax %B ．a (1-x %)C ．a +x %D ．a (1+x %)9.下列代数式： (1)2213x y ； (2)ab ÷c 2； (3) m n ； (4) 223a b -； (5)2x (a+b )； (6)ab ·2. 符合代数式书写要求的有几个？答：（ ）A ．1个B ．2个C ．3个D ．4个10.已知m 个人n 天的工作量为P ，则一人一天的工作量为（ ）.A ．mnPB ．mn PC ．P mnD ．Pm n11.用语言叙述代数式a 2-b 2，正确的是（ ）A ．a ，b 两数的平方差B ．a 与b 差的平方C ．a 与b 的平方的差D ．b ，a 两数的平方差12.某养鸡专业户大力发展养鸡事业，前年养鸡x 只，去年比前年增加15%，则去年比前年增加了几只（ ）A ．15%x 只B ．（1+15%）x 只C ．x +15%只D ．75%x 只 13.出的代数式错误的是（ ）；A ．a 与4的积的平方记为4a 2B ．a 与b 的积的倒数为ab 1C ．减去5等于x 的数是x +5D ．比x 除以y 的商小3的数为3x y-14.乙数为a ，甲数比乙数小40%，则甲数为（ ）A ．a -40%B ．40%aC ．（1-40%）aD ．（1+40%）a15.a 是一个三位数，b 是一个两位数，若把b 放在a 的左边，组成一个五位数，则这个五位数为（ ）．A ．b a +B ．10b a +C ．100b a +D ．1000b a +16.一项工程，甲队单独做需要m 天完成，乙队单独做需要n 天完成，两队合作需要多少天完成？答：（ ）A ．m+nB ．2m n + C ．11m n + D ．111m n + 17.把a 千克盐溶于b 千克水中，取这样的盐水c 千克.其中含盐（ ） A ．a c b 千克 B ．a c a b ++千克 C ．bc a b +千克 D ．ac a b+千克 18.设n 为任意自然数，用代数式表示：(1)被3除余1的数；(2)被5除余3的数；(3)被b 除余r 的数．19.一张长为a 宽为b 的铁板(a>b )，从四个角截去四个边长为x 的小正方形 2b x ⎛⎫< ⎪⎝⎭，做成一个无盖的盒子，用代数式表示：(1)无盖盒子的外表面积；（用两种方法）(2)无盖盒子的容积．20.如果a 名同学b 小时内共运c 块砖，那么c 名同学以同样的速度搬运a 块砖，所需时间是多少 ？21.某商场将进价a 元的货物提价40%后销售，后因积压又按售价的60%出售，用代数式表示实际的售价，问这次是亏了还是赚了？22.（1）已知0|42|32=-+++x y x ）（，试求多项式322--+x y x 的值．（2）已知多项式34ax bx ++，在2x =时，其值为 8，试求2x =-时，其多项式的值．23.完成某项工作，甲独做要a 小时完成，乙独做要比甲多用2小时，若甲乙合作x 小时后，乙再独做y 小时，则两人共同完成的工作量为．答案:1．C2.D3.D4.D5.C6.B7.C8.D9.C10.C11.A12.A13.A14.C15.D16.D17.D18.(1)3n +1；(2)5n +3；(3)b n+r19.(1)ab －4x 2或(a －2x )(b －2x )+2x (a －2x )+2x (b －2x )(有其它合理答案也对)；(2)(a －2x )(b －2x )x20.因为一名同学一小时运c ab块，所以c 名同学一小时运2c ab 块，所以c 名同学以同样的速度搬运a 块砖所需的时间为：222c a b a ab c ÷=（小时） 21.实际售价为()21140%60%25a a +=元，因为2125a a <，所以这次亏了. 22.(1)24(2)0. 23.1122y x a a a ⎛⎫++⎪++⎝⎭。

冀教版七年级数学上册《3.2 代数式》同步练习-有参考答案一、选择题1.原产量n吨，增产30%之后的产量应为( ).A．(1﹣30%)n吨B．(1＋30%)n吨C．n＋30%吨D．30%n吨2.一个两位数，十位上的数字是a，个位上的数字是b，如果把十位上的数与个位上的数对调，所得的两位数是( )A．ba B．b＋a C．10b＋a D．10a＋b3.一次知识竞赛共有20道选择题，规定：答对一道得5分，不答或答错一道扣1分，如果某位学生答对了x道题，则用式子表示他的成绩为( )A．5x﹣(20＋x)B．100﹣(20﹣x)C．5xD．5x﹣(20﹣x)4.三个连续奇数排成一行，第一个数为x，最后一个数为y，且x＜y.用下列整式表示中间的奇数时，不正确的一个是( )A．x＋2 B．y﹣2 C．x﹣y＋4 D．12(x＋y)5.小明在边长为a的正方形硬纸板上挖去一个最大的圆，则剩余部分的面积是( )A．a2﹣πa2B．a2﹣14πa2C．14(a2﹣πa2) D．a2＋14πa26.一个两位数，个位数字为a，十位数字比个位数字大1，则这个两位数可表示为( )A．11a﹣1 B．11a﹣10 C．11a＋1 D．11a＋107.某商品原价为a元，由于供不应求，先提价20%进行销售，后因供应逐步充足，价格又一次性降价20%，售价为b元，则a，b的大小关系为( )A．b＝a B．b＝0.96a C．b＝a﹣20% D．b＝a+20%8.长方形窗户上的装饰物如图所示，它是由半径均为b的两个四分之一圆组成，则能射进阳光部分的面积是( )A．2a2﹣πb2B．2a2﹣π2b2C．2ab﹣πb2D．2ab﹣π2b29.用一根长为a(单位：cm)的铁丝，首尾相接围成一个正方形，要将它按如图的方式向外等距扩1(单位：cm)，得到新的正方形，则这根铁丝需增加( )A．4 cm B．8 cm C．(a＋4) cm D．(a＋8) cm10.把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为( )A．12 B．14 C．16 D．18二、填空题11.如果手机通话每分钟收费m元，那么通话n分钟收费元.12.与3x-y的和是8的代数式是________.13.某厂第一年生产a件产品，第二年比第一年增加了20%，则两年共生产产品件.14.一个两位数，十位上的数字是2，个位上的数字是x，这个两位数是 .15.某影剧院第一排有30个座位，以后的每一排都比前一排多4个座位，则第n排的座位是 .16.下图是某同学一次旅游时在沙滩上用石子摆成的小房子．观察图形的变化规律，写出第n个小房子用了块石子．三、解答题17.用代数式表示：(1)m的倒数的3倍与m的平方差的50%；(2)x的14与y的差的14；(3)甲数a与乙数b的差除以甲、乙两数的积.18.用代数式表示图中阴影部分的面积.19.一个花坛的形状如图所示，它的两端是半径相等的半圆，求：(1)花坛的周长l；(2)花坛的面积S；(3)若a=8m，r=5m，求此时花坛的周长及面积(π取3.14).20.如图，四边形ABCD与四边形CEFG是两个边长分别为a、b的正方形．（1）用a、b的代数式表示三角形BGF的面积；（2）当a=4cm，b=6cm时，求阴影部分的面积．21.为了节约用水，某市决定调整居民用水收费方法，规定如果每户每月用水不超过20吨，每吨水收费3元；如果每户每月用水超过20吨，那么超过部分每吨水收费3.8元.小红看到这种收费方法后，想算算她家每月的水费，但她不清楚家里每月用水是否超过20吨.(1)如果小红家每月用水15吨，那么水费是______元；如果小红家每月用水35吨，那么水费是______元.(2)如果用字母x表示小红家每月用水的吨数，那么小红家每月的水费该如何用含x 的代数式表示呢？答案1.B2.C.3.D.4.C5.B.6.D.7.B8.D.9.B10.C11.答案为：mn12.答案为：-3x ＋y ＋8；13.答案为：2.2a.14.答案为：20＋x.15.答案为：4n ＋26.16.答案为：(n 2＋4n).17.解：(1)；(2)14(14x ﹣y)； (3)(a ﹣b)÷ab.18.解：(1)(a ＋b)2﹣a 2﹣b 2. (2)14πa 2＋14πb 2. 19.解：(1)l=2πr ＋2a.(2)S=πr 2＋2ar.(3)当a=8m ，r=5m 时，l=2π×5＋2×8=10π＋16≈47.4(m) S=π×52＋2×8×5=25π＋80≈158.5(m 2).20.解：21.解：(1)每月用水15吨时，水费为45元.每月用水35吨时，水费为3.8×(35－20)＋60=117(元).(2)①如果每月用水不超过20吨，水费为3x元；②如果每月用水超过20吨，水费为3.8(x－20)＋60=(3.8x－16)元.。

冀教版数学七年级上册第三章代数式同步测试3.2代数式本次测试共计分为三部分，单选、填空和解答题，总分100分，时间为60分钟。

一、选择题（共计10题，每题5分，共计50分）1、x 表示一个两位数，y 表示一个两位数，把x 放在y 的左面，末位再添上1得到一个五位数，这个五位数等于（ ）.A ．1000x+y+1B ．xy1C ．1000x+10y+1D ．x+y+12、在下列表述中，不能表示代数式“4a ”的意义的是( )A ．4的a 倍B ．a 的4倍C ．4个a 相加D ．4个a 相乘3、东西湖区域出租汽车行驶2千米以内包括2千米的车费是10元，以后每行驶1千米，再加元．如果某人坐出租汽车行驶了m 千米是整数，且，则车费是 A.元 B. 元 C. 元 D . 元 4、下列语句不正确的是（ ）.A ．0是代数式B ．a 是代数式C ．x 的3倍与y 的14的差表示为134x y -D ．s =πr 2是代数式5、下列选项中，列出的代数式错误的是( )A ．a 与4的积的平方记为4a 2B ．a 与b 的积的倒数为1abC ．减去5等于x 的数是x ＋5D ．比x 除以y 的商小3的数为x y －3 6、下列各式：2m ，0，-2n ，b a ，221,,x x y a b ab x+-+=中，代数式有（ ） A ．4个 B ．5个 C ．6个 D ．7个7、已知三个连续奇数，最大的一个是m ，用代数式表示其他两个数应为( )A ．m －1，m －2B ．m －2，m －3C ．m －3，m －4D ．m －2，m －48、某商店举办促销活动，促销的方法是将原价x 元的商品以元出售，则下列说法中，能正确表达该商店促销方法的是A. 原价降价50元后再打7折B. 原价打7折后再降价50元C. 原价降价50元后再打3折D. 原价打3折后再降价50元9、若a增加x%后得到b，那么b=( ).A．ax% B．a(1-x%) C．a+x% D．a(1+x%)10、乙数为a，若甲数比乙数小40%，则甲数为( )A．a－40% B．40%a C．(1－40%)a D．(1＋40%)a二、填空题（共计5题，每题4分，共计20分）1、小明用a元钱去购买某种练习本．这种练习本原价每本b元，现在每本降价1元，则他现在可以购买到这种练习本的本数为______2、某养鸡专业户大力发展养鸡事业，前年养鸡x只，去年比前年增加15%，则去年比前年增加了几只______。

第4课时 探索规律知识点1 探索数、式规律1．2018·梧州中考 按一定规律排列的一列数依次为2，3，10，15，26，35，…，按此规律排列下去，则这列数中的第100个数是( )A ．9999B ．10000C ．10001D ．100022．2018·宜昌中考 1261年，我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律，比欧洲的相同发现要早三百多年，我们把这个三角形称为“杨辉三角”，请观察图3－ 2－2中的数字排列规律，则a ，b ，c 的值分别为( )图3－2－2A ．a ＝1，b ＝6，c ＝15B ．a ＝6，b ＝15，c ＝20C ．a ＝15，b ＝20，c ＝15D ．a ＝20，b ＝15，c ＝63．2018·牡丹江中考 一列数1，4，7，10，13，…，按此规律排列，第n 个数是____________． 4．某数学小组的10名同学站成一列做报数游戏，规则是从前面第一名同学开始，每名同学依次报自己顺序数的倒数的2倍加1，第1名同学报⎝⎛⎭⎫21＋1，第2名同学报⎝⎛⎭⎫22＋1，第3名同学报⎝⎛⎭⎫23＋1，…，这样得到的n 个数的积为________．5．观察下列关于自然数的等式： 32－4×12＝5；① 52－4×22＝9；② 72－4×32＝13；③ …根据上述规律解决下列问题：(1)完成第四个等式：92－4×______2＝______；(2)写出你猜想的第n 个等式________________(用含n 的代数式表示)． 知识点2 探索图形规律6．2018·迁安期末 如图3－2－3，用围棋子按下面的规律摆图形，则摆第n 个图形需要围棋子的枚数是( )图3－2－3A ．4n ＋1B ．3n ＋1C ．4n ＋2D ．3n ＋27．2018·烟台 如图3－2－4所示，下列图形都是由相同的玫瑰花按照一定的规律摆成的，按此规律摆下去，第n 个图形中有120朵玫瑰花，则n 的值为( )图3－2－4A．28 B．29 C．30 D．318．2018·青海图3－2－5是由火柴棒按某种规律搭成的，第(1)个图案中有2个正方形，第(2)个图案中有5个正方形，第(3)个图案中有8个正方形，…，则第(5)个图案中有______个正方形，第n个图案中有________个正方形．图3－2－59．图3－2－6所示的图案是晋商大院窗格的一部分，其中“○”代表窗纸上所贴的剪纸．图3－2－6(1)第1个图案中所贴剪纸“○”的个数为________，第2个图案中所贴剪纸“○”的个数为________，第3个图案中所贴剪纸“○”的个数为________；(2)用代数式表示第n个图案中所贴剪纸“○”的个数，并求当n＝100时，所贴剪纸“○”的个数．10．2019·启东期中按一定规律排列的一列数依次为－3，6，－11，18，－27，…，按此规律排列下去，这列数中第9个数及第n个数(n为正整数)分别是() A．83，－n2＋2 B．－83，(－1)n(n2＋2)C．83，(－1)n(n2＋2) D．－83，－n2＋211．2017·自贡填在图3－2－7所示的各正方形中四个数之间都有相同的规律，根据这种规律m的值为()图3－2－7A．180 B．182 C．184 D．18612．如图3－2－8，一串按一定规律排列的珠子，珠子的颜色有黑色和白色两种，这串珠子有一部分被一个长方体的盒子遮住了，则这串珠子被盒子遮住的部分有珠子()图3－2－8A．6颗B．3颗C．29颗D．27颗13．2019·南宁期中图3－2－9是一组有规律的图案，第1个图案由4，第2个图案由7，第3个图案由10，第4个图案由13，…，则第n－1(n为正整数，n≥2)个图案由________组成．图3－2－914．如图3－2－10，用同样规格的灰、白两色正方形瓷砖铺设长方形地面，请观察图3－2－10所示的图形，探究并回答下列问题．图3－2－10(1)第4个图(n＝4)中，共有白色瓷砖________块；第n个图中，共有白色瓷砖________块．(2)第4个图(n＝4)中，共有瓷砖________块；第n个图中，共有瓷砖________块．(3)如果每块灰色瓷砖4元，每块白色瓷砖3元，那么当n＝10时，共需花多少钱购买瓷砖？15．如图3－2－11，某餐厅中，一张桌子可坐6人，有以下两种摆放方式：(1)当有n张桌子时，两种摆放方式各能坐多少人？(2)一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种摆放方式来摆放餐桌？为什么？图3－2－11教师详解详析【备课资源】【详解详析】1．A [解析] 因为第奇数个数2＝12＋1，10＝32＋1，26＝52＋1，…，第偶数个数3＝22－1，15＝42－1，25＝62－1，…，所以第100个数是1002－1＝9999.故选A.2．B [解析] 根据图形可知每个数字等于上一行的左右两个数字之和，所以a ＝1＋5＝6，b ＝5＋10＝15，c ＝10＋10＝20.故选B.3．1＋3(n －1)4.12(n ＋1)(n ＋2) [解析] 第1名同学报的数是21＋1＝31， 第2名同学报的数是22＋1＝42，第3名同学报的数是23＋1＝53，…第n 名同学报的数是2n ＋1＝n ＋2n，所以，这样得到的n 个数的积为31×42×53×…×n ＋2n ＝12(n ＋1)(n ＋2)．5．(1) 4 17(2)(2n ＋1)2－4n 2＝4n ＋16．D [解析] 因为第1个图形中有5枚，即(3×1＋2)枚；第2个图形中有8枚，即(3×2＋2)枚；第3个图形中有11枚，即(3×3＋2)枚；…所以第n个图形中有(3n＋2)枚．故选D.7．C[解析] 由图可得，第n个图形中有玫瑰花4n朵，令4n＝120，得n＝30.故选C.8．14(3n－1)[解析] 因为第(1)个图形中正方形的个数2＝3×1－1，第(2)个图形中正方形的个数5＝3×2－1，第(3)个图形中正方形的个数8＝3×3－1，…所以第(5)个图形中正方形的个数为3×5－1＝14，第n个图形中正方形的个数为(3n－1)．9．解：(1)5811(2)第n个图案中所贴剪纸“○”的个数为3n＋2，当n＝100时，所贴剪纸“○”的个数为100×3＋2＝302.10．B[解析] 根据数值的变化规律可得：第一个数：－3＝(－1)1(12＋2)，第二个数：6＝(－1)2(22＋2)，第三个数：－11＝(－1)3(32＋2)，则第9个数：(－1)9(92＋2)＝－83，第n个数：(－1)n(n2＋2)．故选B.11．C[解析] 观察已知数据的规律，因为3×5－1＝14；5×7－3＝32；7×9－5＝58；…；所以m＝13×15－11＝184.故选C.12．D[解析] 黑白珠子排列的规律：1白1黑，1白2黑，1白3黑，1白4黑，…，1白n黑，这串珠子被盒子遮住的部分有5黑，1白6黑，1白7黑，1白(8－2)黑，所以珠子有(5＋7＋8＋1＋8－2)＝27(颗)．故选D.13．[3(n－1)＋1][解析] 观察发现第一个图形有3×1＋1＝4(个)三角形；第二个图形有3×2＋1＝7(个)三角形；第三个图形有3×3＋1＝10(个)三角形；…第(n－1)个图形有[3(n－1)＋1]个三角形．14．解：(1)第4个图中，共有白色瓷砖4×5＝20(块)；第n个图中，共有白色瓷砖n(n＋1)块．故答案为20，n(n＋1)．(2)第4个图中，共有瓷砖(4＋2)×(4＋3)＝42(块)；第n个图中，共有瓷砖(n＋2)(n＋3)块．故答案为42，(n＋2)(n＋3)．(3)4×(4×10＋6)＋3×(10×11)＝184＋330＝514(元)．答：共需花514元钱购买瓷砖．15. 解：(1)第一种摆放方式中，第一张桌子坐6人，后边多一张桌子多坐4人，即有n 张桌子时，可坐人数为6＋4(n－1)．第二种摆放方式中，第一张桌子坐6人，后边多一张桌子多坐2人，即有n张桌子时，可坐人数为6＋2(n－1)．(2)打算用第一种摆放方式来摆放餐桌．理由：当n＝25时，6＋4(25－1)＝102(人)，6＋2(25－1)＝54(人)．因为102>98，54＜98.所以选用第一种摆放方式来摆放餐桌．。

3.2 第4课时 探索规律一、选择题1．给定一列按规律排列的数：12，25，310，417，…，则这列数的第6个数是( ) A. 637 B.635 C.531 D.7392．图K －29－1的每个表格中的四个数都是按相同规律填写的．图K －29－1根据此规律确定x 的值为( )A. 135 B ．170 C ．209 D ．2523．2017·烟台用棋子摆出下列一组图形：图K －29－2按照这种规律摆下去，第n 个图形用的棋子个数为A ．3nB ．6nC ．3n ＋6D ．3n ＋3二、填空题4．观察下面各式的变形规律：11×2＝1－12；12×3＝12－13； 13×4＝13－14；… 若n 为正整数，请你猜想1n （n ＋1）＝________． 5．用灰、白两种颜色的正方形纸片，按灰色纸片数逐渐加1的规律拼成一列图案，如图K－29－3所示：图K－29－3(1)第4个图案中有白色纸片________张；(2)第n个图案中有白色纸片________张．三、解答题6．如图K－29－4所示，观察点阵图形和与之相对应的等式，探究其中的规律．图K－29－4(1)请你在④和⑤后面的横线上分别写出相对应的等式；(2)素养提升观察图K－29－5①②③中阴影部分的面积：图K－29－5(1)设图①②③中阴影部分的面积分别为S1，S2，S3，请你分别求出S1，S2，S3；(2)若按图K－29－5的规律在这个正方形内排列着5行5列的相同小圆，其他部分为阴影，请你猜想阴影部分的面积为______．1．A2．[解析] C 根据图中所示，可知道第n 个表格左上角的数字为n ，左下角的数字为n ＋1；然后根据4－1＝3，6－2＝4，8－3＝5，10－4＝6，…，可得从第一个表格开始，右上角的数与左上角的数的差分别是3，4，5，…，n ＋2，据此求出a 的值，最后根据每个表格中右下角的数＝左下角的数×右上角的数＋左上角的数，可知x 的值．因为a ＋(a ＋2)＝20，所以a ＝9，由于b ＝a ＋1＝9＋1＝10，所以x ＝20b ＋a ＝20×10＋9＝209.3．[解析] D 借助图形特点，可以发现：第一个图形棋子的个数为3×1＋3；第二个图形棋子的个数为3×2＋3；第三个图形棋子的个数为3×3＋3；…第n 个图形棋子的个数为3n ＋3.4.1n －1n ＋15．(1)13 (2)(3n ＋1)6．(1)④4×3＋1＝4×4－3 ⑤4×4＋1＝4×5－3(2)4(n －1)＋1＝4n －3 [素养提升]解：(1)S 1＝a 2－π·(a 2)2＝a 2－πa24；S 2＝a 2－4π·(a 4)2＝a 2－4π·a216＝a 2－πa24；S 3＝a 2－9π·(a 6)2＝a 2－9π·a 236＝a 2－πa24.(2)a 2－πa24。

第4课时探索规律知识点1 探索数、式规律1．[2017·百色]观察以下一列数的特点：0，1，－4，9，－16，25，…，则第11个数是( )A．－121 B．－100 C．100 D．1212．[2017·日照]观察图3－2－4中的“品”字形中各数之间的规律，根据观察到的规律得出a的值为( )图3－2－4A．23 B．75 C．77 D．1393．[2017·铜仁]观察下列关于自然数的式子：4×12－12，①4×22－32，②4×32－52，③…根据上述规律，则第2017个式子的值是( )A．8064 B．8065 C．8066 D．80674．[教材习题A组第3题变式]观察下列等式：第1层：1＋2＝3；第2层：4＋5＋6＝7＋8；第3层：9＋10＋11＋12＝13＋14＋15；第4层：16＋17＋18＋19＋20＝21＋22＋23＋24；…在上述的数字宝塔中，从上往下数，2017在第________层．( )A．41 B．45 C．43 D．445．[2017·郴州]已知a1＝－32，a2＝55，a3＝－710，a4＝917，a5＝－1126，…，则a8＝________．6．[2017·沧州模拟]观察下面两行数：2，4，8，16，32，64，…①5，7，11，19，35，67，…②根据你发现的规律，取每行数的第10个数，求得它们的和是________(要求写出最后的计算结果)．7．观察下列关于自然数的等式：32－4×12＝5；①52－4×22＝9；②72－4×32＝13；③…根据上述规律解决下列问题：(1)完成第四个等式：92－4×______2＝______；(2)写出你猜想的第n个等式(用含n的代数式表示)．知识点2 探索图形规律8．[2017·黔西南州]如图3－2－5，用相同的小正方形按照某种规律进行摆放，则第8个图形中小正方形的个数是( )图3－2－5A．71 B．78 C．85 D．899．[2017·重庆A卷]图3－2－6所示的图形都是由同样大小的平行四边形按照一定规律所组成的，其中第1个图形中一共有3个平行四边形，第2个图形中一共有7个平行四边形，第3个图形中一共有13个平行四边形，…，按此规律排列下去，第9个图形中平行四边形的个数为( )图3－2－6A．73 B．81 C．91 D．10910. [2017·天水]观察图3－2－7中的“蜂窝图”：图3－2－7则第n个图案中的“”的个数是________．(用含有n的代数式表示)11．[2017·白银]如图3－2－8，每个图形都是由完全相同的小梯形按一定规律组成的．如果第1个图形的周长为5，那么第2个图形的周长为________，第2017个图形的周长为________．图3－2－812．图3－2－9所示的图案是晋商大院窗格的一部分，其中“○”代表窗纸上所贴的剪纸．图3－2－9(1)第1个图中所贴剪纸“○”的个数为________，第2个图中所贴剪纸“○”的个数为________，第3个图中所贴剪纸“○”的个数为________；(2)用代数式表示第n个图中所贴剪纸“○”的个数，并求当n＝100时，所贴剪纸“○”的个数．13．[2017·武汉]按照一定规律排列的n个数：－2，4，－8，16，－32，64，…，若最后三个数的和为768，则n为( )A．9 B．10 C．11 D．1214．[2017·自贡]填在图3－2－10所示的各正方形中四个数之间都有相同的规律，根据这种规律m的值为( )图3－2－10A．180 B．182 C．184 D．18615. [2017·扬州]在一列数：a1，a2，a3，…，a n中，a1＝3，a2＝7，从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这一列数中的第2017个数是( )A．1 B．3 C．7 D．916. [2017·德州]观察图3－2－11所示的图形，它是把一个三角形分别连接这个三角形三边的中点，构成4个小三角形，挖去中间的一个小三角形(如第1个图)；对剩下的三个小三角形再分别重复以上做法(如第2个图，第3个图)，…，将这种做法继续下去，则第6个图中挖去的三角形的个数为( )图3－2－11A．121 B．362 C．364 D．72917．如图3－2－12，用同样规格的灰、白两色正方形瓷砖铺设长方形地面，请观察图3－2－12所示的图形，探究并回答下列问题．图3－2－12(1)第4个图(n＝4)中，共有白色瓷砖________块；第n个图中，共有白色瓷砖________块．(2)第4个图(n＝4)中，共有瓷砖________块；第n个图中，共有瓷砖________块．(3)如果每块灰色瓷砖4元，每块白色瓷砖3元，那么当n＝10时，共需花多少钱购买瓷砖？18．如图3－2－13，某餐厅中，一张桌子可坐6人，有以下两种摆放方式：(1)当有n张桌子时，两种摆放方式各能坐多少人？(2)一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种摆放方式来摆放餐桌？为什么？图3－2－13【详解详析】1．B [解析] 0＝－(1－1)2，1＝(2－1)2，－4＝－(3－1)2，9＝(4－1)2，－16＝－(5－1)2，…，所以第11个数是－(11－1)2＝－100.故选B.2．B [解析] 因为上边的数为连续的奇数1，3，5，7，9，11，…，左下的数为21，22，23，…，所以b＝26＝64.因为上边的数与左下的数的和正好等于右下的数，所以a＝11＋64＝75.故选B.3．D [解析] 由①②③三个等式可得，减数是从1开始连续奇数的平方，被减数是从1开始连续自然数的平方的4倍，所以第2017个式子的值是4×20172－(2×2017－1)2＝8067.故选D.4．D [解析] 因为第1层的第1个数为1＝12，第2层的第1个数为4＝22，第3层的第1个数为9＝32，所以第44层的第1个数为442＝1936，第45层的第1个数为452＝2025，所以2017在第44层．故选D.5.1765[解析] 由题意给出的5个数可知a n＝(－1)n2n＋1n2＋1，当n＝8时，a8＝1765.6．2051 [解析] 根据题意可知，①中第10个数为210＝1024；②中第10个数为210＋3＝1027，故它们的和为1024＋1027＝2051.7．解：(1) 4 17(2)第n个等式为(2n＋1)2－4n2＝4n＋1.8．D [解析] 第1个图形中共有小正方形的个数为2×2＋1，第2个图形中共有小正方形的个数为3×3＋2，第3个图形中共有小正方形的个数为4×4＋3，…，则第n个图形中共有小正方形的个数为(n＋1)2＋n，所以第8个图形共有小正方形的个数为9×9＋8＝89.故选D.9．C [解析] 第1个图形中一共有3个平行四边形，3＝12＋2；第2个图形中共有7个平行四边形，7＝22＋3；第3个图形中共有13个平行四边形，13＝32＋4；…；第n个图形中平行四边形的个数为n2＋n＋1；第9个图形中平行四边形的个数为92＋9＋1＝91.故选C.10．3n＋1 [解析] 由题意可知每个图都比前一个多出了3个“”，所以第n个图案中“”的个数为4＋3(n－1)＝3n＋1.11．8 6053 [解析] 因为第1个图形的周长为2＋3＝5，第2个图形的周长为2＋3×2＝8，第3个图形的周长为2＋3×3＝11，…，所以第2017个图形的周长为2＋3×2017＝6053.12．解：(1)5 8 11(2)第n个图中所贴剪纸“○”的个数为3n＋2，当n＝100时，所贴剪纸“○”的个数为100×3＋2＝302.13．B [解析] 由题意，得第n个数为(－2)n，那么(－2)n－2＋(－2)n－1＋(－2)n＝768，当n为偶数时，整理得3×2n－2＝768，解得n＝10；当n为奇数时，整理得－3×2n－2＝768，则求不出整数．故选B.14．C [解析] 观察已知数据的规律，因为3×5－1＝14；5×7－3＝32；7×9－5＝58；…；所以m＝13×15－11＝184.故选C.15．B [解析] 依题意，得a1＝3，a2＝7，a3＝1，a4＝7，a5＝7，a6＝9，a7＝3，a8＝7，…，观察可知6个数为一个循环，2017÷6＝336……1，所以a2017＝a1＝3.故选B.16．C [解析] 第1个图挖去中间的1个小三角形，第2个图挖去中间的(1＋3)个小三角形，第3个图挖去中间的(1＋3＋32)个小三角形，…，则第6个图挖去中间的(1＋3＋32＋33＋34＋35)个小三角形，即第6个图挖去中间的364个小三角形．故选C.17．解：(1)第4个图中，共有白色瓷砖4×5＝20(块)；第n个图中，共有白色瓷砖n(n＋1)块．故答案为20，n(n＋1)．(2)第4个图中，共有瓷砖 (4＋2)×(4＋3)＝42(块)；第n个图中，共有瓷砖(n＋2)(n ＋3)块．故答案为42，(n＋2)(n＋3)．(3)4×(4×10＋6)＋3×(10×11)＝184＋330＝514(元)．答：共需花514元钱购买瓷砖．18. 解：(1)第一种摆放方式中，第一张桌子坐6人，后边多一张桌子多坐4人，即有n 张桌子时，可坐人数为6＋4(n－1)＝4n＋2.第二种摆放方式中，第一张桌子坐6人，后边多一张桌子多坐2人，即有n张桌子时，可坐人数为6＋2(n－1)＝2n＋4.(2)打算用第一种摆放方式来摆放餐桌．理由：当n＝25时，4×25＋2＝102(人)，102＞98，2×25＋4＝54(人)，54＜98. 所以选用第一种摆放方式来摆放餐桌．。

《代数式4》同步练习1.寻找规律计算1 - 2+3 - 4+5 - 6+…+2015 - 2016等于 ()A.0B. - 1C. - 1008D.10082.如图所示的是某年5月的日历表,任意圈出一竖列上相邻的三个数,发现这三个数的和不可能是()A.27B.36C.40D.543.观察下列图形,则第n个图形中三角形的个数是 ()A.2n+2B.4n+4C.4n– 4D.4n4.数字解密:第一个数是3=2+1,第二个数是5=3+2,第三个数是9=5+4,第四个数是17=9+8,…,观察并猜想第六个数是.5.按如图所示的方式,用火柴棒拼成三角形.(1)当三角形的个数是5个时,用了多少根火柴棒?(2)要拼成n个三角形需要多少根火柴棒?【能力提升】6.如图所示,按这种规律堆放圆木,第10堆应有()A.50根B.60根C.65根D.55根7.某百货大楼进了一批花布,出售时要在进价的基础上,加上一定的利润,其数量x(米)与售价y(元)如下表:下列公式中正确的是()A.y=0.8x+0.3B.y=8+0.3xC.y=(8+0.3)xD.y=8+0.3+x8.观察下列图形,根据变化规律推测第100个与第个图形的位置相同.(填“1”“2”或“3”)9.已知:2+=22×,3+=32×,4+=42×,5+=52×……若10+=102×符合前面的式子的规律,则a+b=.10.观察下面的点阵图形和与之相对应的等式,探究其中的规律.(1)请你在④和⑤后面的横线上分别写出相对应的等式;①4×0+1=4×1 - 3;。