理想气体基本热力过程
- 格式:doc
- 大小:296.50 KB
- 文档页数:12










例举出理想气体的四个基本热力过程及其过程方程式。
理想气体是指在恒定温度下,所有气体分子间不存在相互作用力的气体体系。
对于理想气体,四个基本热力过程依次是等温过程、绝热过程、等压过程和等体过程,下面我们来一一介绍这四个过程。
一、等温过程等温过程是指理想气体在恒定温度下发生的过程,此时系统内的温度不变。
在等温过程中,理想气体的压强与体积成反比例关系,即PV = 常数,其中P为气体的压强,V为气体的体积。
二、绝热过程绝热过程是指理想气体在没有任何能量交换的情况下发生的过程。
在绝热过程中,由于没有热量的交换,温度会发生变化。
绝热过程中理想气体的状态方程为PV^{γ} = 常数,其中γ为理想气体的绝热指数。
三、等压过程等压过程是指理想气体在恒定压强下发生的过程。
在等压过程中,理想气体的体积与温度成正比例关系,即V/T = 常数。
等压过程的状态方程为V/T = 常数,其中V为气体的体积,T为气体的绝对温度。
四、等体过程等体过程是指理想气体在恒定体积下发生的过程。
在等体过程中,理想气体的压强与温度成正比例关系,即P/T = 常数。
等体过程的状态方程为P/T = 常数,其中P为气体的压强,T为气体的绝对温度。
通过以上介绍,我们可以看出四个基本热力过程对应的状态方程式分别是:等温过程 PV = nRT、绝热过程PV^{γ} = 常数、等压过程 V/T = 常数、等体过程 P/T = 常数。
在实际应用中,这四个基本热力过程是非常重要的。
通过对这些过程的掌握,我们可以更好地理解理想气体的物理变化规律,为一些实际问题的解决提供指导意义。
理想气体的基本热力过程热力设备中,热能与机械能的相互转化,通常是通过气态工质的吸热、膨胀、放热、压缩等热力过程来实现的。
实际的热力过程都很复杂,而且几乎都是非平衡、非可逆的过程。
但若仔细观察会发现,某些常见过程非常近似一些简单的可逆过程。
常见的主要有四种简单可逆过程-基本热力过程,指系统某一状态参数保持不变的可逆过程。
包括定容过程、定压过程、定温过程和绝热过程。
我们以1kg理想气体的闭口系统为例来分析这几种基本热力过程,分析方法包括5点:(1)依据过程特点建立过程方程式;(2)由过程方程和理想气体状态方程确定初、终态基本状态参数之间的关系,即P1、v1、T1和P2、v2、T2之间的关系;(3)绘制过程曲线;我们主要绘制两种坐标图P-v图和T-s图,因为P-v图上可以表示过程中做功量的多少,而T-s图上可以表示过程中吸收或放出热量的多少;(4)分析计算△u,△h,△s;(5)分析计算过程的热量q和功w。
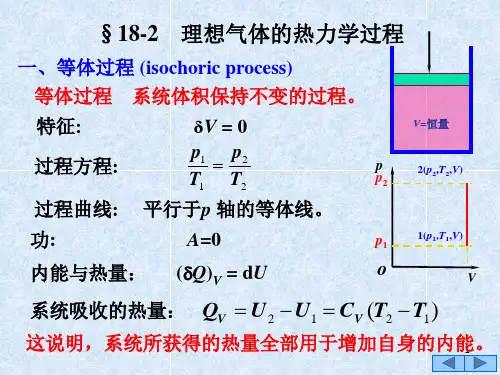
一、定容过程定容过程即工质的容积在整个过程中维持不变,dv=0,通常是一定量的气体在刚性容器中进行定容加热或定容放热。
(1)依据过程特点建立过程方程式定容过程的特点是体积保持不变,所以建立过程方程式:v=常数;或dv=0或v1=v2(2)由过程方程和理想气体状态方程确定初、终态基本状态参数之间的关系过程方程式:v1=v2理想气体状态方程:112212Pv P v T T = 由以上两个方程可以得到初末基本状态参数之间的关系:122211v v P T P T =⎧⎪⎨=⎪⎩ 即定容过程中工质的压力与温度成正比。
(3)绘制过程曲线;定容过程有两种情况:定容加热和定容放热。
(4)分析计算△u ,△h ,△s ;2211v v u u u c dT c T ∆=-==∆⎰ 2211p p h h h c dT c T ∆=-==∆⎰ 222111ln ln ln p v v v P P s c c c v P P ∆=+=或222111ln ln ln v v T v T s c R c T v T ∆=+= (5)分析计算过程的热量q 和功w 。
容积变化功:210w Pdv ==⎰ 根据q=△u+w 可得:v q u c T =∆=∆总结:定容过程中系统与外界无容积变化功,加给工质的热量全部用于增加工质的热力学能,而没有热能与机械能的转化。
二、定压过程定压过程即工质的压力在整个过程中维持不变,dP=0,工程上使用的加热器、冷却器、燃烧器、锅炉等设备都是在接近定压的情况下工作的。
(1)依据过程特点建立过程方程式定压过程的特点是压力保持不变,所以建立过程方程式:P=常数;或dP=0或P 1=P 2(2)由过程方程和理想气体状态方程确定初、终态基本状态参数之间的关系过程方程式:P 1=P 2 理想气体状态方程:112212Pv P v T T = 由以上两个方程可以得到初末基本状态参数之间的关系:122211P P v T v T =⎧⎪⎨=⎪⎩ 即定压过程中工质的比容与温度成正比。
(3)绘制过程曲线;定压过程有两种情况:定压加热和定压放热。
T-s 图上曲线是对数曲线,从上图可知,定容过程与定压过程在T-s 图上都是对数曲线,但定压线的斜率小,更为平坦。
(4)分析计算△u ,△h ,△s ;2211v v u u u c dT c T ∆=-==∆⎰ 2211p p h h h c dT c T ∆=-==∆⎰ 222111ln ln ln p v p v P v s c c c v P v ∆=+=或222111ln ln ln p p T P T s c R c T P T ∆=-= (5)分析计算过程的热量q 和功w 。
容积变化功:22121211()w Pdv P v v Pv Pv RT RT R T ==-=-=-=∆⎰ 根据q=△u+w 可得:v p q u w c T R T c T =∆+=∆+∆=∆总结:工质在定压过程中吸入的热量等于焓的增加量,放出的热量等于焓的降低量。
三、定温过程定温过程即工质的温度在整个过程中维持不变,dT=0。
(1)依据过程特点建立过程方程式定温过程的特点是温度保持不变,所以建立过程方程式:T=常数;或dT=0或T 1=T 2(2)由过程方程和理想气体状态方程确定初、终态基本状态参数之间的关系过程方程式:T 1=T 2 理想气体状态方程:112212Pv P v T T = 由以上两个方程可以得到初末基本状态参数之间的关系:122112T T P v P v =⎧⎪⎨=⎪⎩ 即定温过程中工质的压力与比容成反比。
(3)绘制过程曲线;定容过程有两种情况:定容加热和定容放热。
(4)分析计算△u ,△h ,△s ;22110v v u u u c dT c T ∆=-==∆=⎰ 22110p p h h h c dT c T ∆=-==∆=⎰ 222111ln ln ln p T P P s c R R T P P ∆=-=-或222111ln ln ln v T v v s c R R T v v ∆=+= (5)分析计算过程的热量q 和功w 。
容积变化功:22221111ln ln v RT w Pdv dv RT v RT v v ====⎰⎰ 根据q=△u+w 可得:21ln v q w RT v == 总结:定温过程中内能变化为零,吸热量全部用于对外做膨胀功。
四、绝热过程绝热过程是指与外界无热量交换的过程,即0q δ=或q=0;(1)依据过程特点建立过程方程式0q δ=或q=0 另外根据revq ds T δ=得到:ds=0即可逆的绝热过程是熵不变的过程,定熵过程。
现实中严格的绝热过程是不存在的,但当过程进行的无限快时,工质与外界来不及换热,这种过程可近似认为是绝热的。
绝热过程的过程方程式有另外一种表达方式:P k v =常数 其中k pv c c =,是比热容比,又叫绝热指数,当比热取定值比热时,k 是与状态无关的常数。
(2)由过程方程和理想气体状态方程确定初、终态基本状态参数之间的关系过程方程式:1122k k Pv P v = 理想气体状态方程:112212Pv P v T T = 由以上两个方程可以得到初末基本状态参数之间的关系:22111211212211()()()kk k k P v P v T v T v T P T P --=== (3)绘制过程曲线;定容过程有两种情况:定容加热和定容放热。
(4)分析计算△u ,△h ,△s ;2211v v u u u c dT c T ∆=-==∆⎰ 2211p p h h h c dT c T ∆=-==∆⎰ 0s ∆=(5)分析计算过程的热量q 和功w 。
绝热过程q=0;根据q=△u+w 得:w=-△u=v c T -∆绝热(定熵)过程是内能与膨胀功之间的转换。
多变过程前面我们讨论的几种基本热力过程,定容、定压、定温和绝热,都会有一个参数保持不变,要么是体积,要么是压力、温度或熵。
但在实际热机中,有些过程,工质的状态参数都会有显著的变化,即PVT 没有一个是恒定不变的,而且工质与外界之间的换热量也不可以忽略不计,即s 也是变化的非绝热过程。
这时,我们就不能将实际过程简化为上述几种基本热力过程。
但通过实验发现,多数过程的P-v 关系曲线往往比较接近指数方程式,即 P n v =常数热力学中个,热力过程符合该式的变化过程称做多变过程。
其中,n 为多变指数,取值在(-∞,﹢∞)之间。
n 为定值。
实际的热力过程往往非常复杂,主要有两种情况:(1)整个过程并不完全符合P n v =常数,但整个过程中n 值变化不大,比如:前半段过程符合2P v =常数,中间段过程符合 2.1P v =常数,后半段过程符合2.2P v =常数,那么我们可以用一个不变的n 的平均值来代替实际中变化的n 。
(2)n 的变化较大时,则将热力过程分成几段,每一段作为一个n 不变的简单的多变过程。
我们对于多变过程的分析,同样有前面的5项内容。
(1)依据过程特点建立过程方程式多变过程的过程方程式为:P n v =常数这个方程式比较具有普遍性,将n 取不同的值,它可以代表前面我们讲的四种基本热力过程中的任意一种。
定压过程:n=0定容过程:n=±∞定温过程:n=1绝热过程:n=k(2)由过程方程和理想气体状态方程确定初、终态基本状态参数之间的关系过程方程式:1122n n Pv P v =理想气体状态方程:112212Pv P v T T = 由以上两个方程可以得到初末基本状态参数之间的关系:22111211212211()()()nn n n P v P v T v T v T P T P --=== (3)绘制过程曲线;在P-v 图和T-s 图上,可逆的多变过程是一条任意的双曲线,过程线的相对位置取决于n 的值,我们先把前面讲的四种基本热力过程的过程曲线画在图上,然后再找n 值不同时的曲线。
P-v 图和T-s 图上都以定容线为分界线,多变指数n 按顺时针方向递增。
在热机和制冷、热泵循环中,最常遇到的过程是介于1<n<k 之间,即大多数的实际热力过程介于定温和绝热过程之间。
(4)分析计算△u ,△h ,△s ;2211v v u u u c dT c T ∆=-==∆⎰ 2211p p h h h c dT c T ∆=-==∆⎰ 222111ln ln ln p T P P s c R R T P P ∆=-=-或222111ln ln ln v T v v s c R R T v v ∆=+=或222111ln ln ln p v p v P v s c c c v P v ∆=+=(5)分析计算过程的热量q 和功w 。
n n q c T =∆其中n c 称为多变比热1n v n k c c n -=- 根据根据q=△u+w 得:w=q-△u= ()1v v n k c c T n --∆- 过程曲线比较重要的一个作用是判断过程中△u 、w 、q 的正负。
1、判断△u 的正负以定温线为界,在T-s 图上,任何同一起点的多变过程,若变化曲线位于定温线上方,则△u 为正,若变化过程曲线位于定温线下方,则△u 为负。
在P-v 图上,任何同一起点的多变过程,若变化曲线位于定温线右上方,则△u 为正,若变化曲线位于定温线左下方,则△u 为负。
2、判断w 的正负以定容线为界,在T-s 图上,任何同一起点的多变过程,若变化曲线位于定容线右下方,则w 为正,若变化过程曲线位于定容线左上方,则w 为负。
在P-v 图上,任何同一起点的多变过程,若变化曲线位于定容线右方,则w 为正,若变化曲线位于定温线左方,则w 为负。