留数在定积分计算上的应用
- 格式:ppt
- 大小:1.90 MB
- 文档页数:45

留数定理在定积分中的应用摘 要 留数理论是复积分和复级数理论相结合的产物,利用留数定理可以把沿闭路的积分转化为计算孤立点处的留数.此外,在数学分析及实际问题中,往往一些被积函数的原函数不能用初等函数表示,有时即便可以,计算也非常复杂.我们利用留数定理可以把要求的积分转化为复变函数沿闭曲线的积分,从而把待求积分转化为留数计算.本文介绍留数定义和留数定理以及一些改进的留数计算方法,并讨论了留数理论在定积分计算中的应用。
关键词 留数定理;定积分;应用1. 留数定义定理及其他一些定理1.1 留数的定义设函数()f z 以有限点a 为孤立点,即()f z 在点a 的某个去心邻域0z a R <⋅<内解析,则积分()()1:,02f z dz z a R i ρρπΓΓ⋅=<<⎰为()f z 在点a 的留数,记为:()Re z as f z =.1.2 留数定理介绍留数定理之前,我们先来介绍复周线的柯西积分定理:设D 是由复周线012C C C C --=+++…nC -所围成的有界连通区域,函数()f z 在D 内解析,在_D D C =+上连续,则()0Cf z dz =⎰.定理1 []1(留数定理) 设()f z 在周线或复周线C 所范围的区域D 内,除12,,a a …,n a 外解析,在闭域_D D C =+上除12,,a a …,n a 外连续,则( “大范围”积分)()()12Re knz a k Cf z dz i s f z π===∑⎰.2.留数定理在计算积分中的应用2.1 形如()20cos ,sin f x x dx π⎰型的积分这里()cos ,sin f x x 表示cos ,sin x x 的有理函数,并且在[]0,2π上连续,把握此类积分要注意,第一:积分上下限之差为2π,这样当作定积分时x 从0经历变到2π,对应的复变函数积分正好沿闭曲线绕行一周.第二:被积函数是以正弦和余弦函数为自变量。

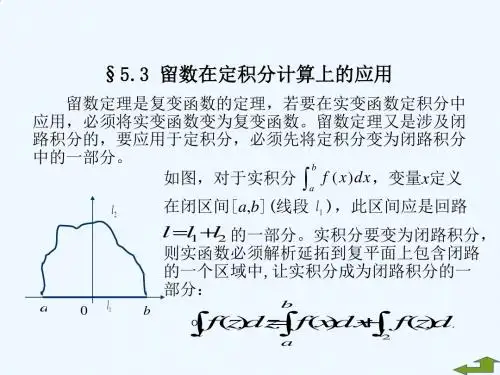








留数定理在定积分中的应用1. 留数定义及留数定理1.1 留数的定义设函数()f z 以有限点a 为孤立点,即()f z 在点a 的某个去心邻域0z a R <⋅<内解析,则积分()()1:,02f z dz z a R i ρρπΓΓ⋅=<<⎰为()f z 在点a 的留数,记为:()Re z as f z =.1.2 留数定理介绍留数定理之前,我们先来介绍复周线的柯西积分定理:设D 是由复周线012C C C C --=+++…n C -所围成的有界连通区域,函数()f z 在D 内解析,在_D D C =+上连续,则()0Cf z dz =⎰.定理1 []1(留数定理) 设()f z 在周线或复周线C 所范围的区域D 内,除12,,a a …,n a 外解析,在闭域_D D C =+上除12,,a a …,n a 外连续,则( “大范围”积分)()()12Re knz a k Cf z dz i s f z π===∑⎰. (1)证明 以k a 为心,充分小的正数k ρ为半径画圆周:k k z a ρΓ⋅=(1,2,k =…,n )使这些圆周及内部均含于D ,并且彼此相互隔离,应用复周线的柯西定理得()()1knk Cf z dz f z dz =Γ=∑⎰⎰,由留数的定义,有()()2Re kkz a f z dz i s f z π=Γ=⎰.特别地,由定义得 ()2Re kkz a f z dz i s π=Γ=⎰,代入(1)式得 ()()12Re knz a k Cf z dz i s f z π===∑⎰.2.留数定理在定积分中的应用利用留数计算定积分活反常积分没有普遍的实用通法,我们只考虑几种特殊类型的积分.2.1 形如()20cos ,sin f x x dx π⎰型的积分这里()cos ,sin f x x 表示cos ,sin x x 的有理函数,并且在[]0,2π上连续,把握此类积分要注意,第一:积分上下限之差为2π,这样当作定积分时x 从0经历变到2π,对应的复变函数积分正好沿闭曲线绕行一周.第二:被积函数是以正弦和余弦函数为自变量。
探究留数定理在求解不同类型积分上的应用留数定理是复变函数中的一个重要定理,它在求解不同类型积分上有着广泛的应用。
从留数定理的定义和性质出发,我们可以探究留数定理在求解不同类型积分上的具体应用。
本文将从留数定理的基本原理出发,分别探讨留数定理在求解定积分、无穷积分、奇异积分和复积分中的应用,以及其在物理和工程等实际问题中的应用。
一、留数定理的基本原理留数定理是复变函数理论中的一个重要定理,它给出了复变函数在孤立奇点处的留数与该函数在该奇点所作割线积分之间的关系。
设F(z)在孤立奇点z0处解析,即在z0的某个邻域内解析,并且在z0处的留数为R,若C是以z0为内点的简单闭曲线,则有\[\oint _{C} \! F ( z ) \, dz = 2\pi iR\]留数定理的一个重要推论是:如果f(z)在孤立奇点z0的邻域内解析,并且在z0处的留数为R,则有其中Res(f,zk)表示f(z)在zk处的留数。
这个结论为我们在实际问题中利用留数定理求解积分提供了重要的理论基础。
二、留数定理在定积分中的应用留数定理在求解定积分中有着重要的应用。
对于某些定积分,可以通过构造合适的闭合曲线,并利用留数定理来求解。
考虑积分\[\int_{0}^{2\pi}\frac{d\theta}{a+b\cos\theta}\]可以构造复平面上的单位圆上的积分路径,然后利用留数定理来求解这个积分。
在复平面上,积分变量z的标量为e^{i\theta},则积分可以表示为其中z0和z-1分别是函数f(z)在z=0处和z=∞处的留数。
通过计算这两个留数,我们可以求解出原定积分的值。
留数定理在求解无穷积分中也有重要的应用。
考虑积分可以通过构造合适的积分路径,然后利用留数定理来求解这个无穷积分。
我们可以沿着实轴积分,然后在上半平面做半圆弧积分。
留数定理还可以用来解决奇异积分。
考虑积分六、留数定理在物理和工程实际问题中的应用留数定理在物理和工程实际问题中也有着重要的应用。
一绪论1研究背景及意义留数,也称残数,是指函数在其孤立奇点处的积分. 综观复分析理论的早期发展,这一概念的提出对认识孤立奇点的分类及各类奇点之间的关系具有十分重要的意义. 同时,它将求解定积分的值的方法推进到一个新的阶段,通过函数的选取,积分路径的选取等等,求解出了许多被积函数的原函数解不出来的情况,为积分理论的发展奠定了充分的基础[1 ] .1825 年,柯西(Cauchy) 在其《关于积分限为虚数的定积分的报告》中,基于与计算实积分问题的情形的类比,处理了复积分的相关问题,并给出了关于留数的定义[2 ] . 随后,柯西进一步发展和完善留数的概念,形成了如下定义[3],若函数f(z)在D(a,r)\{a}上全纯,其中r>0.a为f (z)的孤立奇点,f(z)在a的留数定义为Res(f,a)=柯西所给的这一定义一直沿用到了现在,推广到了微分方程,级数理论及其他一些学科, 并在相关学科中产生了深远影响, 成为一个极其重要的概念. 因而很自然地产生了这样一个问题:柯西为什么要定义这一概念或者说,什么因素促使柯西提出了留数的定义显然这一问题对于全面再现柯西的数学思想,揭示柯西积分理论乃至整个复分析研究的深层动机等具有极为重要的理论意义和历史意义.二留数定理2.1 留数的定义如果函数f(z)在点a的邻域K:|z-a|<R内解析,围线C全含于K(包围a或不包围a),则但如果a是f(z)的孤立奇点,即f(z)在点a的去心邻域K-{a}:0<|z-a|<R内解析,围线C是K-{a}中包围a的围线,则上式不一定成立,故留数定义如下:定义如果函数f(z)以a为孤立奇点,即f(z)在K-{a}:0<|z-a|<R中解析,则积分:|z-a|=称为f(z)在点a处的留数或残数(residue),记作f(z),或简记为Resf(a)或Res(f,a)。
显然,只要,上述积分的数值与的大小无关.2.2 Cauchy 留数定理利用Cauchy 积分定理,可以推出下面关于围线积分的Cauchy 留数定理设函数f(z)在围线或复围线C所围成的区域D中有孤立奇点a1、a2、……、an,,此外f(z)在上解析,则有.利用Cauchy 留数定理,只要算出各孤立奇点处的留数,即可得出围线积分,所以关键在于计算留数.2.3留数的算法设a为f(z)的n阶极点,f(z)=,其中在点a解析,则证:推论 1 设a为f(z)的一阶极点则.推论 2 设a为f(z)的一阶极点, 则.三留数定理的应用3.1用留数定理计算实积分A.计算型积分这里表并且在[0,2π]上连续.若命z=,则,,。