开孔处应力集中系数的简化计算

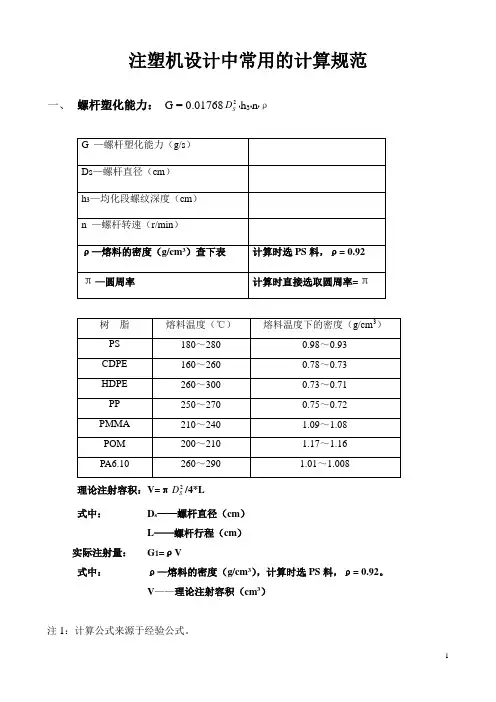
注塑机设计中常用的计算规范一、螺杆塑化能力：G = 0.017682D·h3·n·ρSD/4*L理论注射容积：V=π2S式中：D s——螺杆直径（cm）L——螺杆行程（cm）实际注射量：G1=ρV式中：ρ—熔料的密度（g/cm3），计算时选PS料，ρ= 0.92。

V——理论注射容积（cm3）注1：计算公式来源于经验公式。

二、螺杆的强度根据螺杆最常见的破坏，是在加料段螺槽根径处发生断裂，所以螺杆的强度计算就以此处计算其应力。

σr =224τσ+c≤〔σ〕 式中：压缩应力σc =sF P 0= 210⎪⎪⎭⎫ ⎝⎛d D 0p剪应力 τ=stW M 材料许用应力〔σ〕=ny σ式中三、熔胶筒的壁厚：（按厚壁筒计算中的能量理论，校核其强度或计算壁厚）熔胶筒的总应力σr = P 1322-K K ≤ 〔σ〕熔胶筒壁厚 δ= 2b D (P3-〔σ〕〔σ〕－ 1 ) 式中部分熔胶筒的K 值四、螺杆驱动功率：采用经验公式计算N s = C·5.2D·n4.1S式中：N s——螺杆驱动功率（kw）C ——与螺杆结构参数及传动方式有关的系数取C=0.00016D s——螺杆直径（cm）n ——螺杆转速（r/min）螺杆所需扭矩与直径及转速之间的关系，可用下式表示：M t = 10α·D mS式中：M t——螺杆扭矩（N·m）——螺杆直径（cm）DSα——比例系数，对于热塑性塑料α=1.2～1.5m ——由树脂性能而定的指数，m=2.7～3螺杆的驱动功率一般需留20～30%的余量，以作备用。

五、传动轴的强度：传动轴最常见的破坏是在承受扭矩的最小截面处发生断裂，所以传动轴的强度计算就以此处进行计算：σr =224τσ+c ≤〔σ〕 式中：压缩应力σc = sF P= 210⎪⎪⎭⎫ ⎝⎛d D 0p剪应力 τ=stW M 材料许用应力〔σ〕=ny σ式中六、轴 承1、基本额定动负荷计算：C =Tn dm h f f f f f ·P ＜ C r （或C a ） 式中C ——基本额定动负荷计算值（N ）； P ——当量动负荷，见下式（N ）； h f ——寿命系数，按表7-2-4选取； n f ——速度系数，按表7-2-5选取；m f ——力矩负荷系数，力矩负荷较小时1.5，力矩负荷较大时2； d f ——冲击负荷系数，按表7-2-6选取； T f ——温度系数，按表7-2-7选取；C r ——轴承尺寸及性能表中所列径向基本额定动负荷（N ）； C a ——轴承尺寸及性能表中所列轴向基本额定动负荷（N ）。

- 43 -第5期加氢反应器设计中接管载荷的处理方法范强强（安徽实华工程技术股份有限公司， 安徽 合肥 230091）[摘 要] 炼油化工行业关键设备—加氢反应器设计中接管载荷的计算和处理方法，应考虑接管载荷引起壳体局部应力的问题及非标法兰设计中接管载荷的问题。

主要的处理方法包括利用SW6软件中局部应力程序的计算方法、有限元应力分析方法以及SW6软件中法兰的计算方法和法兰当量压力估算方法。

[关键词] 加氢反应器；接管载荷；局部应力；非标法兰作者简介：范强强（1988—），男，安徽阜阳人，2014年毕业于华东理工大学化工过程机械专业，硕士研究生，中级工程师。

从事石油化工设备设计工作。

图2 封头接管载荷局部应力有限元分析加氢反应器是加氢装置中的核心设备，造价昂贵，处于高温、高压、临氢和硫化氢腐蚀的恶劣工况，其安全运行与否关系到整个装置的安全生产。

因此，加氢反应器对设计的安全性和经济性要求很高，反应器设计过程中必须考虑接管载荷的影响。

接管载荷对反应器设计的影响，主要包括接管载荷对设备壳体的局部应力和接管载荷对非标法兰设计的影响。

1 接管载荷对壳体的局部应力容器壳体除了承受工作时介质产生的内部压力外，还承受外部配管重量以及安装过程中装配误差和工作过程中的温度波动所产生的附加载荷，这些附加载荷称为接管载荷（力、力矩和扭矩）。

实际计算中，接管载荷主要考虑工艺配管的载荷，包括管道自重和工艺物料重量引起的载荷，以及管道的热胀冷缩引起的载荷。

接管载荷主要通过配管专业的管道应力分析软件CAESAR Ⅱ的静力分析获得，包括三向力Fx 、Fy 、Fz 和三个面上的力矩Mxy 、Myz 、Mzx 。

壳体的局部应力就是由作用在法兰上的这三个力和三个力矩引起的。

对于中低压和非高温压力容器，接管载荷较小，考虑设备余量，一般不会成为容器厚度的控制因素。

但是对于高温高压设备，特别是接管比较大的管口，其接管载荷较大，开孔的应力集中系数也更大，因此一般均需要核算接管载荷引起的局部应力。

第三章 平面模型应力计算方法（1学时）从光弹性实验中已经获得了两类资料，一类是等差线，即表示两主应力差相等的线；另一类是等倾线，即表示主应力方向相同的线。

就是说，从实验中已经得到了两个条件。

现在讨论如何根据这两个条件来计算模型中的应力值。

相关知识：应力圆、点的应力状态、平衡方程等，注意区分材料力学和弹性力学中关于剪应力符号的规定。

§3-1 边界应力和应力集中一、边界应力光弹性模型实验中，计算应力是从边界开始的。

边界应力是直接根据模型边界上所出现的等差线条纹级数求出的。

因为根据公式021σσσn =-可知，等式右边的条纹级数n 从等差线图获得，б0是模型条纹值，是一个已知的常数。

对于模型的无载边界只有沿边界切线方向的一个主应力存在，另一个为零。

根据钉压法完全确定了这个未知的主应力是拉还是压，即201σσσσn n =-=或 （3-1）如果边界法向方向有载，则载荷是做实验时加上去的，是一个已知值，稍加推理（主应力方向即外载荷方向），边界应力值就可以确定。

工程上的问题，大多数是需要知道最大应力值及其发生的部位，再用最大应力来控制构件的强度设计，或者在发生最大应力处适当加强或采取其它相应措施，以确保构件强度的可靠性。

实际上，当构件受力后，最大应力往往就发生在构件的边界上，对于全面确定边界值（而不是边界个别值）来说，应用光弹性模型实验法比之于其它任何方法都更方便、更有效。

例如图3-1a 所示平面开孔眼杆，受拉力P=700N ．其等差线如图3-1b 所示，欲求眼杆洞孔水平直径边界点A 处的应力值。

眼杆材料条纹值级⋅=m kN f /5.120。

眼杆厚度t=5mm ，洞孔处宽度b=13.7mm ，读出A 点处的条纹级数n A =9.56级（图中D=26mm ，d=3mm ）。

根据钉压法可知点A 受拉，应用公式（3-1）得到边界点A 的应力为MPa t f n A A 9.23005.0105.1256.930=⨯⨯==σ二、应力集中应力集中现象由等差线图清楚地展现出来。

拉伸、压缩与剪切1基本概念及知识要点1.1 基本概念轴力、拉（压）应力、力学性能、强度失效、拉压变形、胡克定律、应变、变形能、静不定问题、剪切、挤压。

以上概念是进行轴向拉压及剪切变形分析的基础，应准确掌握和理解这些基本概念。

1.2 轴向拉压 的内力、应力及变形1．横截面上的内力：由截面法求得横截面上内力的合力沿杆的轴线方向，故定义为轴力F N ，符号规定：拉力为正，压力为负。

工程上常以轴力图表示杆件轴力沿杆长的变化。

2．轴力在横截面上均匀分布，引起了正应力，其值为F Aσ=N正应力的符号规定：拉应力为正，压应力为负。

常用的单位为MPa 、Pa 。

3．强度条件强度计算是材料力学研究的主要问题之一。

轴向拉压时，构件的强度条件是[]F Aσσ=≤N可解决三个方面的工程问题，即强度校核、设计截面尺寸及确定许用载荷。

4．胡克定律线弹性范围内，杆的变形量与杆截面上的轴力F N 、杆的长度l 成正比，与截面尺寸A成反比；或描述为线弹性范围内，应力应变成正比，即F l l E EAσε∆==N式中的E 称为材料的弹性模量，EA 称为抗拉压刚度。

胡克定律揭示在比例极限内，应力和应变成正比，是材料力学最基本的定律之一，一定要熟练掌握。

1.3 材料在拉压时的力学性能材料的力学性能的研究是解决强度和刚度问题的一个重要方面。

材料力学性能的研究一般是通过实验方法实现的，其中拉压试验是最主要、最基本的一种试验，由它所测定的材料性能指标有：E —材料抵抗弹性变形能力的指标；b s σσ,—材料的强度指标；ψδ, —材料的塑性指标。

低碳钢的拉伸试验是一个典型的试验。

详见教材，应理解本部分知识。

1.4 简单拉压静不定问题1． 未知力的个数超过静力平衡方程个数的问题为静不定问题，其中未知力可以是结构的约束反力或构件的内力。

2． 解决静不定问题，除列出静力平衡方程外，还需列出一定数量的补充方程，这些补充方程可由结构各部分变形之间的几何关系以及变形和力之间的物理关系求得，将补充方程和静力平衡方程联立求解，即可得出全部未知力。

非标准机械设计中轴强度校核的简化方法非标准机械设计中，轴的强度校核是一个重要的计算步骤。

由于设计和制造方法的不同，轴的形状和材料也会有所不同，因此轴的强度校核需要根据具体情况进行计算。

以下是一些简化方法：
1.基于经验公式。

轴的强度可以根据经验公式进行估算。

这些公式基于经验数据和复杂的数学模型，可以给出轴的最大扭矩、剪切力和弯曲力等参数，然后将这些参数与轴的几何形状和材料特性相结合，得出轴的最大强度。

2.应力集中系数法。

应力集中系数法是一种简单但精确的轴强度计算方法。

它考虑到了轴上不同部位的应力集中程度，并将最大应力与轴的材料特性相比较以确定轴的强度。

该方法通常适用于需要考虑阶梯、凸起、凹陷和螺纹等特殊形状的轴。

3.有限元分析。

有限元分析是一种准确的轴强度计算方法。

它将轴的几何形状和材料特性建模成有限元模型，并使用计算机模拟不同的力学载荷，以确定轴的应力和变形情况。

这种方法计算精度高，但需要复杂的机械建模和数值计算技术。

以上是非标准机械设计中轴强度校核的简化方法，但需要注意的是，轴的强度计算必须在满足设计和制造要求的前提下进行。

因此，在实际应用中，应根据具体情况综合考虑各种方法的优缺点，选取合适的方法进行计算。

“压力容器设计”习题答案一、选择题：1．我国钢制压力容器设计规范<<GB150-89>>采用的强度理论为： （ A ）（A ）Ⅰ； （B ）Ⅱ； （C ）Ⅲ； （D ）Ⅳ。

2．毒性为高度或极度危害介质PV ≥0.2MPa ·m 3的低压容器应定为几类容器？ （ C ）（A ）Ⅰ类； （B ）Ⅱ类； （C ）Ⅲ类； （D ）其他。

3.一空气贮罐，操作压力为0.6Mpa ，操作温度为常温，若设计厚度超过10毫米，则下列碳素钢材中不能够使用的钢种为： （ A ）（A ）Q235AF （A3F ）；（B ）Q235A （A3）；（C ）20R 。

4．在弹性力学平面应力问题中，应力和应变分量分别为： （ C ）（A ）бZ ≠0、εZ ＝0；（B ）бZ ≠0、εZ ≠0 ；（C ）бZ ＝0、εZ ≠0。

5．受均匀内压作用的球形容器，经向薄膜应力σϕ和周向薄膜应力σθ的关系为 （ C ）（A ）σϕ < σθ （B ）σϕ > σθ （C ）σϕ＝σθ＝pR/2t （D ）σϕ＝σθ＝pR/t6．受均匀内压作用的圆柱形容器，经向薄膜应力σϕ和周向薄膜应力σθ的关系为 （ B ）（A ）σθ=2σϕ＝pR/2t ；（B ）σθ=2σϕ＝pR/t ；（C ）σϕ＝2σθ=pR/t ；（D ）σϕ＝2σθ＝pR/2t7．均匀内压作用的椭圆形封头的顶点处，经向薄膜应力σϕ和周向薄膜应力σθ的关系为 ( A )。

A 、σϕ＝σθB 、σϕ < σθC 、σϕ > σθD 、σϕ > 1/2σθ8．由边缘力和弯矩产生的边缘应力，影响的范围为（A ）Rt ； （B ）Rt 2； （C ）Rt 2； （D ）Rt9．受均布横向载荷作用的周边简支圆形薄平板，最大径向弯曲应力在： （ A ）（A ） 中央； （B ）周边；（ C ）1/2半径处； D. 3/8半径处。