有效应力集中系数 Kσ

1200
σB/ M a P
附图3-4 钢材的表面质量系数 βσ 附图
返回
附表3-8 零件与轴过盈配合处的 ε 值 附表 σ
直径 /mm 配合 400 H7/r6 30 H7/k6 H7/h6 H7/r6 50 H7/k6 H7/h6 H7/r6 >100 H7/k6 H7/h6 2.25 1.69 1.46 2.75 2.06 1.80 2.95 2.22 1.92 500 2.50 1.88 1.63 3.05 2.28 1.98 3.28 2.46 2.13 600 2.75 2.06 1.79 3.36 2.52 2.18 3.60 2.70 2.34 σB/MPa 700 3.00 2.25 1.95 3.66 2.76 2.38 3.94 2.96 2.56 800 3.25 2.44 2.11 3.96 2.97 2.57 4.25 3.20 2.76 900 3.50 2.63 2.28 4.28 3.20 2.78 4.60 3.46 3.00 1000 3.75 2.82 2.44 4.60 3.45 3.00 4.90 3.98 3.18 1200 4.25 3.19 2.76 5.20 3.90 3.40 5.60 4.20 3.46
表示零件的尺寸系数。 通常用 εσ 、ετ 表示零件的尺寸系数。 附图3-3 附图 附图3-2 附图 尺寸系数愈小表示疲劳强度降低愈大。 尺寸系数愈小表示疲劳强度降低愈大。 螺纹联接件的尺寸系数（因截面为圆形，故只有尺寸影响） 螺纹联接件的尺寸系数（因截面为圆形，故只有尺寸影响） 见下表： 见下表：
三、表面状态的影响
1、表面质量 、 零件表面质量（主要指表面粗糙度，表面粗糙度参数值越小 零件表面质量（主要指表面粗糙度， 疲劳强度越高）对疲劳强度的影响， 疲劳强度越高）对疲劳强度的影响，通常用 βσ 、βτ 表示表面状 态的影响程度。 态的影响程度。 附图3-4 附图 2、表面处理 、 表示。 表面处理对疲劳强度影响用强化系数 βq表示。 附表3-9 附表 附表3-10 附表 附表3-11 附表 音乐欣赏 Flash欣赏 幽默笑话 欣赏 课间休息 写字板 补充材料 上一页 下一页 退出

3—29 某轴只受稳定交变应力的作用，工作应力 σ max=240MPa，σ min=-40MPa。材料的机械性能 σ -1=450MPa，σ s=800MPa，σ 0=700Mpa，轴上危险截面处的 kσ =1.3，ε σ =0.78，β σ =1，β q=1。 ⑴ 绘制材料的简化极限应力图； ⑵ 用作图法求极限应力σ r 及安全系数（按 r=C 加载和无限寿命考虑） ； ⑶ 取[S]=1.3，试用计算法验证作图法求 S 值，并校验此轴是否安全。 解： （1） A 点（ 0，σ -1） ， B 点（σ 0/2，σ 0/2） ，S 点（σs.0） （2） k (
第三章
一、选择题
机械零件的强度
C 。
3—1 零件的截面形状一定，当截面尺寸增大时，其疲劳极限值将随之 A 增加 B 不变 C 降低 D 规律不定
3—2 在图中所示的极限应力图中，工作应力有 C1、C2 所示的两点，若加载规律为 r=常数。在进 行安全系数校核时， 对应 C1 点的极限应力点应取为 A ， 对应 C2 点的极限应力点应取为 B 。 A B1 B B2 C D1 D D2 σ a D1 B1 3—3 同上题，若加载规律为σ m=常数，则对应 C1 点 D2 C1 的极限应力点应取为 C ，对应 C2 点的极限应力点 C2 B2 应取为 D 。 O σS σm A B1 B B2 C D1 D D2 题 3 —2 图 0 3—4 在图中所示的极限应力图中，工作应力点为 C，OC 线与横坐标轴的交角θ =60 ，则该零件 σa 所受的应力为 D 。 A C D 对称循环变应力 B 脉动循环变应力 σ max、σ min 符号（正负）相同的不对称循环变应力 σ max、σ min 符号（正负）不同的不对称循环变应力 o θ C σm 题 3 —4 图

• 尽可能地减小或消除零件表面可能发生的初始裂纹的尺
寸，对于延长零件的疲劳寿命有着比提高材料性能更为
显著的作用。
（3）双向稳定变应力时零件的疲劳强度计算
3. 计算安全系数
4. 不对称循环的变应力
（4）提高机械零件疲劳强度的措施
• 尽可能降低零件上的应力集中的影响
• 可采用减荷槽来降低应力集中的作用；
（4）提高机械零件疲劳强度的措施
• 选用疲劳强度高的材料；
• 提高材料疲劳强度的热处理方法及强化工艺；
• 提高零件的表面质量；
3-2 机械零件的疲劳强度计算
（0）零件的极限应力线图 （1）单向稳定变应力时机械零件的疲劳强度计算 （2）单向不稳定变应力时机械零件的疲劳强度计算 （3）双向稳定变应力时机械零件的疲劳强度计算 （4）提高机械零件疲劳强度的措施
（0）零件的极限应力线图
1. 材料的极限应力线图 2. 零件的极限应力线图
（1）单向稳定变应力时机械零件的疲劳强度计算
计算零件疲劳强度的基本方法: • 零件危险截面上的σmax和σmin；
• 平均应力σm和应力幅σa
• 标出工作应力点M；
• 找出和工作应力 点相对应的疲劳 强度极限； • 计算零件工作的 安全系数。
（1）单向稳定变应力时机械零件的疲劳强度计算
1. 变应力的循环特性保持不变（r = C ）
3. 变应力的最小应力保持不变（σmin = C ）劳极限，分母看成是 一个与原来作用的不对称循环变应力等效的对称循环变应力。
• 应力的等效转化 ：
• 计算安全系数为：
（2）单向不稳定变应力时零件的疲劳强度计算
• 不稳定变应力可分为非规律性的和规律性的两大类。 • 疲劳损伤累积假说：Miner法 则

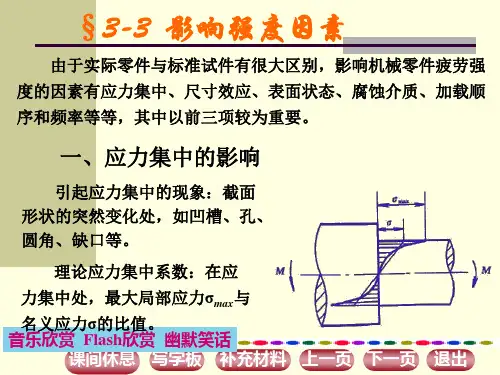
开孔处应力集中系数的简化计算开孔处应力集中系数的简化计算1. 引言在工程设计和分析中，开孔处应力集中是一个常见的问题。

当在材料中添加孔洞或凹槽时，会导致应力场的非均匀分布，从而对材料的力学性能产生负面影响。

准确计算开孔处的应力集中系数对于工程设计和材料选择至关重要。

在本文中，我们将重点讨论开孔处应力集中系数的简化计算方法，以便工程师和研究人员能够更好地理解和应用这一概念。

2. 开孔处应力集中系数的定义开孔处应力集中系数（Stress Concentration Factor，简称SCF）是指材料在受力情况下，开孔处局部应力与远离开孔处应力的比值。

通常用K表示，其计算公式为K=σ_max/σ_nominal，其中σ_max为开孔处的最大应力，σ_nominal为远离开孔处的应力。

在工程设计中，SCF的值可以用来衡量材料在开孔处的应力集中程度，以及对其疲劳寿命和强度的影响。

3. 开孔处应力集中系数的简化计算方法在实际工程中，精确计算开孔处的应力集中系数可能非常复杂，因为需要考虑材料的几何形状、加载方式、以及材料的本构关系等多个因素。

然而，对于一些简单的几何形状和加载情况，我们可以采用一些简化的方法来估算开孔处应力集中系数。

3.1. Neuber's RuleNeuber's Rule是一种常用的简化计算方法，适用于圆形孔洞的应力集中系数估算。

根据Neuber's Rule，对于轴向受拉的材料，开孔处应力集中系数与远离开孔处应力之比可以近似为2。

这种简化计算方法在工程实践中得到了广泛的应用，尤其适用于轴向拉伸载荷作用下的材料。

3.2. Peterson's MethodPeterson's Method是另一种常用的简化计算方法，适用于不同几何形状和加载情况下的应力集中系数估算。

根据Peterson's Method，可以通过查表或计算公式来估算特定几何形状的开孔处应力集中系数。

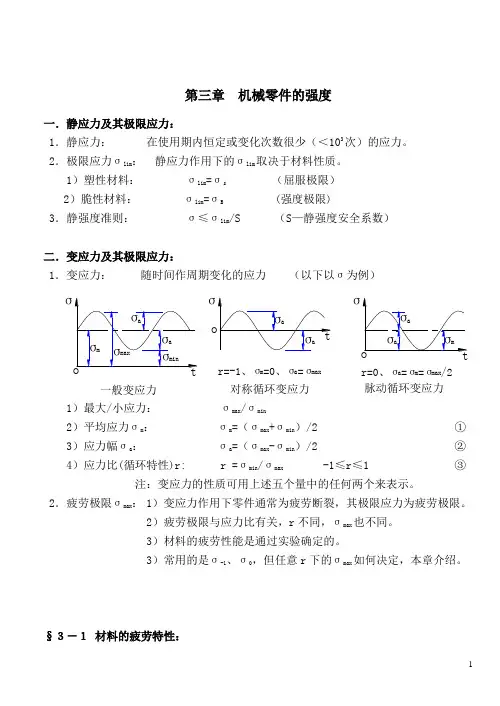
1第三章 机械零件的强度一．静应力及其极限应力：1．静应力： 在使用期内恒定或变化次数很少（＜103次）的应力。

2．极限应力σlim： 静应力作用下的σlim取决于材料性质。

1）塑性材料： σlim =σs （屈服极限）2）脆性材料： σlim=σB (强度极限)3．静强度准则： σ≤σlim/S （S —静强度安全系数）-10max§３－１ 材料的疲劳特性：1．材料的疲劳特性：可用最大应力σmax、应力循环次数N和应力比r表示。

2．材料疲劳特性的确定：用实验测定，实验方法是：1）在材料标准试件上加上一定应力比的等幅变应力，应力比通常为：r=-1或r=02）记录不同最大应力σmax下试件破坏前经历的循环次数N，并绘出疲劳曲线。

3．材料的疲劳特性曲线：有二种1）σ—N疲劳曲线：即一定应力比r下最大应力σmax与应力循环次数N的关系曲线2）等寿命曲线：即一定应力循环次数N下应力幅σa 与平均应力σm的关系曲线2）C点对应的N约为：NC≈1043）这一阶段的疲劳称为应变疲劳或低周疲劳4、CD段：有限寿命疲劳阶段。

试件经历一定的循环次数N后会疲劳破坏实验表明，有限疲劳寿命σrN与相应的循环次数N之间有如下关系：23σm rN ·N = C ( N ≤N D ) （3-1）5、D 点以后： 无限寿命疲劳阶段。

1）无论经历多少次应力循环都不会疲劳破坏。

2）D 点对应的循环次数N 约为：N D =106～25×107 3）D 点对应的应力记为：σr ∞—— 叫持久疲劳极限。

σrN =σr∞( N ＞N D ) （3-2）4）循环基数N O 和疲劳极限σrN D 很大，疲劳试验很费时，为方便起见，常用人为规定一个循环次数N O （称 为循环基数）和与之对应的疲劳极限σrNo（简记为σr ）近似代替N D 和σr ∞6、有限寿命疲劳极限σrN ： 按式（3-1）应有： σm rN·N = σm r ·N O = C （3-1a ）于是：K N ──寿命系数m, N O ──1）钢材（材料）： m = 6～20 ， N O =（1～10）×106 2）中等尺寸零件： m = 9 ， N O = 5×106 3）大尺寸零件： m = 9 ， N O = 107 注： 高周疲劳——曲线CD 及D 点以后的疲劳称作高周疲劳二、等寿命疲劳曲线 图3-2等寿命疲劳曲线——一定循环次数下的疲劳极限的特性。

n n
满足疲劳强度条件。
§12–5 弯扭组合变形构件的疲劳强度计算
1．构件工作安全系数：
n
n n n2 n2
2．强度条件：
n n
例12-3. 阶梯轴如图示。材料为合金钢，σb=920MPa，σ-1 =410MPa， τ-1=240MPa。作用于轴上的弯矩变化于-1000Nm到1000Nm之间，扭矩 变化于0到1500Nm之间。若规定安全系数n=2，试校核轴的疲劳强度。
解：(1)求弯曲正应力
M
0.2 r5
0.2
M
m
axMWmax
1000 (0.05)3
T
81.5MPa
φ50
φ60
T
32
min
为对称循环
(2)求扭转剪应力
max
Tmax Wt
1500 (0.05)3
61.1MPa
16
min 0
a
m
1 2
m
ax
30.6MPa
(3)由轴的尺寸
r 0.1 D1.2
0.77
表面质量系数是
0.87
(3)求工作安全系数
nK 1ma x 0.71.7 44 0.882701351.41
(4)强度校核
n n
满足强度要求。
§12–4 不对称循环下构件的疲劳强度计算
1．构件工作安全系数：
n
K
1 a m
n
K
1 a m
其中：系数ψσ和ψτ与材料有关； 2．强度条件：
4．构件持久极限的计算式：
综合三个方面因素
01K 1 01K 1
其中：σ-1和τ-1表示光滑小试样的持久有限。
§12–3 对称循环下构件的疲劳强度计算

K
( 1)d ( 1)K
K
( 1)d ( 1)K
其中：(σ-1)d和(τ-1)d表示光滑试样的持久有限；(σ-1)K和(τ-1)K表示有 应力集中的相同尺寸试样的持久极限；Kσ和Kτ的值都大于1
2．构件尺寸： 定义尺寸系数
( 1)d 1
( 1)d 1
其中：(σ-1)d和(τ-1)d表示光滑大试样的持久有限；σ-1和τ-1表示光 滑小试样的持久极限；εσ和ετ的值都小于1。
(2)形式二：构件工作安全系数大于等于规定的安全系数
n n n n
例12-1. 阶梯轴如图示。材料为合金钢，σb=920MPa，σs =520MPa， σ-1 =420MPa，τ-1=250MPa。轴在不变弯矩M=850Nm作用下旋转。 若规定n=1.4，试校核轴的强度。。
0.4 r5
解：(1)轴弯曲对称循环， 最大弯曲正应力是
解：(1)由例12_1知 合金钢修正系数
K 1.48 0.77 0.87 0.2
(2)求不对称弯曲的交变应力
max
M max W
1200 (0.04)3
191MPa
32
m in
1
4
max
47.8MPa
a
1 2
( max
min )
71.6MPa
m
1 2
(
max
min )
119MPa
3．构件表面质量： 定义表面质量系数
( 1) ( 1)d
其中：(σ-1)d表示表面磨光试样的持久有限；(σ-1)β表示其它表面 加工情况试样的持久极限；β的值小于1。
4．构件持久极限的计算式：
综合三个方面因素
0 1
K

②计算每个螺栓所需要的预紧力Qp。 计算每个螺栓所需要的预紧力 。 Px 要使底板向右滑移，受到联接接合面摩擦力 要使底板向右滑移， 的阻挡。预紧力Qp使接合面间产生摩擦力 使接合面间产生摩擦力。 的阻挡。预紧力 使接合面间产生摩擦力。Px 使预紧力减小。 对摩擦力无影响，因在M作用 使预紧力减小。M 对摩擦力无影响，因在 作用 底板右部的压力虽然增犬， 下，底板右部的压力虽然增犬，但其左部的压力 却以同样程度减小。考虑Pz 却以同样程度减小。考虑 对预紧力的影响可 得底扳不滑移条件为: 得底扳不滑移条件为 取Kf ＝1.2，f＝0.15（铸铁对干燥加工表面，无 ，＝ （铸铁对干燥加工表面， 垫片） 则 垫片）,则: N
（2）校核螺栓组联接接含面的工作能力 ） ①检查受载时铸铁底板右边缘处走否压溃
式中, 式中 接合面有效面积为 接合面的有效抗弯剖面模量为 m3
m2
MPa 代入得 查表知铸铁（ 查表知铸铁（HT150）的许用挤压应力为 ） MPa 由于σpmax<< [σp]，故接合面右边缘处不致压溃。 由于 ，故接合面右边缘处不致压溃。来自许用拉应力MPa
（2）按第一、三、四强度理论求计算应力 σca ）按第一、 按第一强度理论得 MPa 按第三强度理论得 MPa 按第四理论强度得 MPa
（3）结论 ） 由于许用拉应力 [σ]＝212 MPa 均大于按第 ＝ 一、三、四强度理论所求得的计算应力 σca，所 ， 以该构件强度足够，较为安全。但由于35钢塑性 以该构件强度足够，较为安全。但由于 钢塑性 较好，故用三、四强度理论较合理。 较好，故用三、四强度理论较合理。
机械设计例题
某转动心轴， 例: 某转动心轴，其危险剖面上的平均应力为 σm = 20 MPa，应力幅 σa = 30 MPa，试求最大 ， ， 应力 σmax 、最小应力 σmin 和循环特性 r。 解: 最大应力为 σmax =σm + σa = 20 + 30 = 50 MPa 最小应力为 σmin = σm - σa = 20 - 30 = -10 MPa 循环特性为

σ −1 = 180 MPa ，脉动循环疲劳极限σ 0 = 240 MPa ，略去危险截面处应力集中系
数等综合影响系数 (Kσ ) D 的影响，试求：
（1）等效系数ψ σ 值
（2）安全系数 S 值
7
已 知 材 料 σ −1
=
260 MPa
，σ0
=
360 MPa
，
Kσ εσβ
=
2.5 ， σ a
= 50 MPa ，
9 用压板夹持加工零件,要求夹持力 F = 12000 N ，压板材料的许用弯曲应力
为[σ b ] = 50 MPa 。
1）.分析螺栓装在什么位置压板强度最弱? 2）.按最不利条件定压板厚度 h。
10 某零件材料σ S = 240 MPa ，σ −1 = 180 MPa ，ψ σ = 0.2 ， Kσ = 1.5 ，用作 图法判别：
rT = 10 mm ，宽度 bT = 16 mm ，凸轮宽度 B＝15 mm，两者材料均为合金钢，
E1 = E2 = 2.1 × 105 MPa ，许用接触应力[σ H ] = 2000 MPa ，试校核凸轮在接触点
A 处的接触疲劳强度（摩擦忽略不计）。
注：σ H= 0.418
Fn ⋅ E bρ
16 某零件的材料σ B = 1000 MPa ，σ S = 800 MPa ，σ −1 = 400 MPa ，ψ σ = 0.25， 试画出其简化极限应力图；当工作应力σ max = 300 MPa ，σ min = −100 MPa ，试在 该图上标出此点 K，并说明是否在安全区。
23 某钢制零件已知材料的极限应力图，其σ −1 = 256 MPa ，σ 0 = 456 MPa ， σ S = 0.6σ B ， σ B = 800 MPa ，该零件的有效应力集中系数 Kσ = 1.41，尺寸系数 ε σ = 0.91 ， 表 面 状 态 系 数 β = 1 ， 寿 命 系 数 k N = 1.2 ， 工 作 应 力 的 循 环 特 性 r = −0.268 。

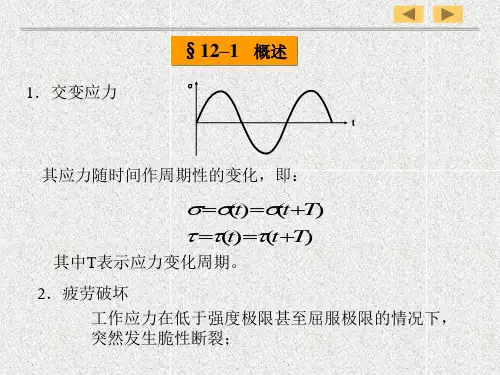
第五章 应力集中一、概述1. 应力集中现象：小范围、高应力（多发生于结构不连续或构件截面突变处）2. 应力集中系数—表示应力(k στ,)集中的程度 k =σσmax 0（σ0表示与应力集中现象无关的名义应力，其取法并不是唯一的）3. 确定值的方法k理论解析方法——弹性力学数值方法——有限元分析试验——光弹、实测⎧⎨⎩⎧⎨⎪⎩⎪二、几种常见结构的应力集中1. 带有圆孔的受拉(压)板(1)无限大板设圆孔半径为，板宽a 2B →∞，均匀受拉，无限远应力为σ0，如图示。

根据弹性理论可知，板内任一点(,)r θ处的应力状态：σσρρρσσρρθτσρρθθθr r =−+−+=+−+=−+−⎧⎨⎪⎩⎪120224120241024114311321232[()()cos ][()()cos ]()sin θ2（其中ρ≡≤a r 1） 高应力区{}5013016o o r a ≤≤≤θ，.，最大应力σmax 发生在与σ0方向相垂直的直径的两端，应力集中系数k ==σmax 03(2)有限板宽的影响 随着B a ↓，，应力集中系数k =↑σmax0（当B a ≥5时，可认为k =3） 2. 椭圆孔的受拉(压)板 [与圆孔对照]设椭圆孔的两半轴长为和b （前者与a σ0方向相垂直），则最大应力σmax 发生的位置与圆孔类似，应力集中系数k a b ==+σσmax 012 ·若a b →∞，则应尽量避免甲板开口长边沿船长方向k →∞⇒3. 矩形开口的受拉(压)板(1)实验表明最大应力发生在矩形角隅圆弧A 点 (2)应力集中系数k f b B r b a r =′=σσmax (,,)0，见书图7-64. 梯形板的弯曲(1)最大应力发生在梯形板的转角处 (2)应力集中系数k =σσmax 0，见书图7-8·若r ↑，则船楼上建端部与主体连接处应以适当的圆弧过渡以减小)应力集中k ↓⇒5. 上建端部主体上的应力集中现象分析参阅书p.225图7-12和7-13船楼：半无限平面边缘甲板室：无限大平面上σσπμπx t T x t T x x T T =⋅=⋅=⋅=⋅⎧⎨⎩+20643026..（σx x ∝1，两侧应力反号） 三、降低应力集中的方法1. 减小应力集中系数或应力集中范围k 圆孔——尽量减小其直径（）椭圆孔——使其长轴∥受力方向（）矩形孔——采用较大的圆弧（）不影响值，但可缩小范围，若则可不必加强使值下降使值下降k d t k k <⎧⎨⎪⎩⎪20 2. 采用加厚板或增设覆板，以覆盖高应力区3. 结构突变处采用过渡结构。

一、单选题（共 30 道试题，共 60 分。

）1. 厚壁玻璃杯倒入开水发生破裂时，裂纹起始于（）A. 内壁B. 外壁C. 壁厚的中间D. 整个壁厚正确答案：B 满分：2 分2.图示结构中，AB杆将发生的变形为（）A. 弯曲变形B. 拉压变形C. 弯曲与压缩的组合变形D. 弯曲与拉伸的组合变形正确答案：D 满分：2 分3. 关于单元体的定义，下列提法中正确的是（）A. 单元体的三维尺寸必须是微小的B. 单元体是平行六面体C. 单元体必须是正方体D. 单元体必须有一对横截面正确答案：A 满分：2 分4. 梁在某一段内作用有向下的分布力时,则在该段内M图是一条 ( )A. 上凸曲线；B. 下凸曲线；C. 带有拐点的曲线；D. 斜直线正确答案：A 满分：2 分5. 在相同的交变载荷作用下，构件的横向尺寸增大，其（）。

A. 工作应力减小，持久极限提高B. 工作应力增大，持久极限降低；C. 工作应力增大，持久极限提高；D. 工作应力减小，持久极限降低。

正确答案：D 满分：2 分6. 在以下措施中（）将会降低构件的持久极限A. 增加构件表面光洁度B. 增加构件表面硬度C. 加大构件的几何尺寸D. 减缓构件的应力集中正确答案：C 满分：2 分7. 材料的持久极限与试件的（）无关A. 材料；B. 变形形式；C. 循环特征；D. 最大应力。

正确答案：D 满分：2 分8. 梁在集中力作用的截面处，它的内力图为（）A. Q图有突变， M图光滑连续；B. Q图有突变，M图有转折；C. M图有突变，Q图光滑连续；D. M图有突变，Q图有转折。

正确答案：B 满分：2 分9.空心圆轴的外径为D，内径为d，α= d / D。

其抗扭截面系数为（）A B CDA.AB. BC. CD. D正确答案：D 满分：2 分10. 在对称循环的交变应力作用下，构件的疲劳强度条件为公式：；若按非对称循环的构件的疲劳强度条件进行了疲劳强度条件校核，则（）A. 是偏于安全的；B. 是偏于不安全的；C. 是等价的，即非对称循环的构件的疲劳强度条件式也可以用来校核对称循环下的构件疲劳强度D. 不能说明问题，必须按对称循环情况重新校核正确答案：C 满分：2 分11. 关于单元体的定义，下列提法中正确的是（）A. 单元体的三维尺寸必须是微小的；B. 单元体是平行六面体；C. 单元体必须是正方体；D. 单元体必须有一对横截面。

《机械设计基础》一.填空题：1.机械设计课程主要讨论通用机械零件和部件的设计计算理论和方法。

2.机械零件设计应遵循的基本准则：强度准则、刚度准则、耐磨性准则、震动稳定性准则。

3.强度：零件抵抗破裂（表面疲劳、压溃、整体断裂）及塑性变形的能力。

1.所谓机架是指机构中作为描述其他构件运动的参考坐标系的构件。

2.机构是机器中的用以传递与转换运动的单元体；构件是组成机构的运动单元；零件组成机械的制造单元。

3.两构件组成运动副必须具备的条件是两构件直接接触并保持一定的相对运动。

4.组成转动副的两个运动副元素的基本特征是圆柱面。

5.两构件通过面接触而形成的运动副称为低副，它引入2个约束，通过点线接触而构成的运动副称为高副，它引入1个约束。

6.机构的自由度数等于原动件数是机构具有确定运动的条件。

7.在机构运动简图上必须反映与机构运动情况有关的尺寸要素。

因此，应该正确标出运动副的中心距，移动副导路的方向，高副的轮廓形状。

1.铰链四杆机构若最短杆与最长杆长度之和小于等于其余两杆长度之和则可能存在曲柄。

其中若最短杆是连架杆，则为曲柄摇杆机构；若最短杆是连杆，则为双摇杆机构；若最短杆是机架，则为双曲柄机构；若最短杆与最长杆长度之和大于其余两杆长度之和则不存在曲柄（任何情况下均为双摇杆机构）2.最简单的平面连杆机构是两杆机构。

3.为保证连杆机构传力性能良好，设计时应使最小传动角γmin≥[γ]4.机构在死点位置时的传动角γ=0°.5.平面连杆机构中，从动件压力角α与机构传动角γ之间的关系是α+γ=90°.6.曲柄摇杆机构中，必然出现死点位置的原动件是摇杆。

7.曲柄滑块机构共有6个瞬心。

8.当连杆机构无急回运动特性时行程速比系数K=1.9.以曲柄为主动件的曲柄摇杆机构、曲柄滑块机构中，可能出现最小传动角的位置分别是曲柄与机架共线、曲柄两次垂直于滑块导路的瞬时位置，而导杆机构λ始终是90°1.凸轮的基圆半径是指凸轮转动中心至理论廓线的最小半径。

应力集中stress concentration受力零件或构件在形状、尺寸急剧变化的局部出现应力显著增大的现象。

如传动轴轴肩圆角、键槽、油孔和紧配合等部位，受力后均产生应力集中。

这些部位的峰值应力从集中点到邻近区的分布有明显的下降，呈现很高的应力梯度d/dx(见图)。

零件的早期失效常发生在应力集中的部位,因此了解和掌握应力集中问题，对于机械零件的合理设计和减少机械的早期失效有重要意义。

应力集中系数是评定应力集中的指标。

用分析计算方法或实验应力分析方法（常用光弹性法）求得静载时局部最大应力与该截面（最小截面）名义平均应力之比，便得到弹性应力集中系数K又称理论应力集中系数，它仅与零件的几何形状和变形形式有关。

但零件的强度不仅与几t何形状有关，也与它的尺寸、材料和载荷的性质有关。

如应力集中对疲劳极限的影响，用Kf 表示K为有效应力集中系数。

f用于拉伸、弯曲变形；越大，对应力集中越敏感。

用于扭转变形,一般静强度越高的材料Kf应力集中使交变应力下零件和构件的强度显著降低，因此设计时应该力求减轻应力集中程度，改善局部状况，尽可能使截面的变化平缓，以降低应力集中的影响。

加大过渡部分的圆角半径、沉割圆角、过渡肩环，或采用减载槽等办法，可使应力的流线从低应力区平滑和缓地过渡到高应力区，降低最大应力峰值。

静载时，塑性材料的屈服能缓和应力集中。

铸铁对应力集中不敏感，故对强度无影响。

用其他脆性材料制造的零件，在静、动载荷时均须考虑应力集中的影响。

应力集中 s tress concentration在物体形状急剧变化处，应力发生局部显著增高的现象。

在工程结构的凹角、缺口、沟槽、孔洞附近均会发生应力集中，其中孔洞附近的应力局部增高称为孔边应力集中。

在水利工程中，大坝的坝踵附近以及坝内廊道附近的应力局部增高是应力集中的典型实例。

孔边应力集中的特点是：①集中性，即在孔洞附近的应力远大于无孔时的应力；②局部性，即在离孔边较远之处（例如几倍孔径之外），应力几乎不受孔的影响，其分布情况与数值大小都几乎与无孔时相同；③在弹性范围内，应力集中程度仅与孔的形状以及受力状态有关，而与荷载的大小无关。

控制预紧力的目的： 预紧力过大，会使联接超载 预紧力不足，可能导致联接失效 重要的螺栓应控制预紧力
拧紧螺母时的力矩和预紧力
T T1 T2
T1

F tan(

)
d2 2
T2

1 3
fF
D13 D12
d03 d02
T

1[d2 2d
tan( )
2f 3d
第五章 螺纹联接与螺旋传动
基本概念：螺纹联接是利用螺纹零件构 成的联接
特 点：构造简单，拆装方便，工作可靠， 标准件，应用广
5-1 螺纹 一、 螺纹的主要参数
d--螺纹大径 d1-螺纹小径 d2--螺纹中径 p--螺距 n--线数
S--导程 --螺纹升角 ，牙型角 --牙型斜角
旋向
二、螺纹副的受力关系、效率和自锁
度 mm，设计时应使 hmin 1.25ds
[ ] —螺栓的许用剪切应力，MPa
[ ] p —螺栓或孔壁材料的许用挤压应 力，MPa
2 、受轴向工作载荷的紧螺栓联接
汽缸盖的联接
（1） 受力分析(见动画)
螺栓受力 被联接件受力
F0

F'

Cb Cb Cm
F
F '' F ' Cm F Cb Cm
1 、普通螺纹(代号：M GB 192-81)
特点：螺纹的牙型角=2=60。因牙型 角大，所以当量摩擦系数大，自锁性能
好，主要用于联接
细牙螺纹与粗 牙螺纹的比较
粗牙：常用
细牙：自锁性能更好。常用于承受冲击、振 动及变载荷、或空心、薄壁零件上及微调装 置中 细牙的缺点：牙小，相同载荷下磨损快，易 脱扣

解：(1)求弯曲正应力
max
M 1000 max 81.5MPa W 3 (0.05) 32 min 为对称循环
T
M
0.2
r5 φ 50
0.2 φ 60
M T
(2)求扭转剪应力
max min
Tmax 1500 61.1MPa Wt (0.05)3 16 0 1 2
§12–4 不对称循环下构件的疲劳强度计算
1．构件工作安全系数：
n
1
K
a m 1
n

K
a m
其中：系数ψ σ 和ψ τ 与材料有关； 2．强度条件：
n n
n n
例12-2. 例12-1阶梯轴受不对称弯矩Mmax=1200Nm和Mmin=300MPa的交互作用。 若规定安全系数n=1.8，试校核轴的疲劳强度。 解：(1)由例12_1知
σ σ σ
max1 max2
σ N1 N2 N0=107
-1
N
为对称循环的疲劳曲线，σ-1是材料的持久极限；
§12–２ 对称循环下，影响构件持久极限因素
1．构件外形突然变化：
定义有效应力集中系数
( 1 ) d K ( 1 ) K ( 1 ) d K ( 1 ) K
其中：(σ-1)d和(τ-1)d表示光滑试样的持久有限；(σ-1)K和(τ-1)K表示有 应力集中的相同尺寸试样的持久极限；Kσ和Kτ的值都大于1 2．构件尺寸： 定义尺寸系数
K 0 1.3 K 1 ( K 0 1) 1.23
0.75
0.78
1
0.1
n
1