结构力学_杨海霞_位移法和力矩分配法汇总
- 格式:doc
- 大小:220.50 KB
- 文档页数:17
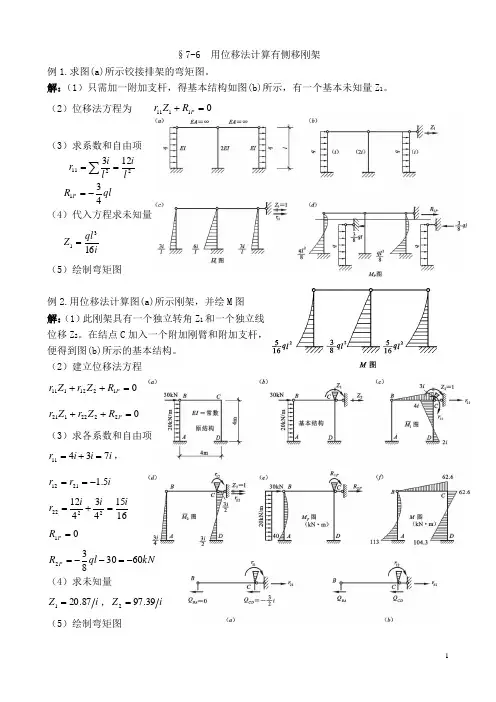
§7-6 用位移法计算有侧移刚架例1.求图(a)所示铰接排架的弯矩图。
解:(1)只需加一附加支杆,得基本结构如图(b)所示,有一个基本未知量Z 1。
(2)位移法方程为 01111=+P R Z r(3)求系数和自由项2211123l il i r ==∑ql R P 431-=(4)代入方程求未知量iql Z 1631=(5)绘制弯矩图例2.用位移法计算图(a)所示刚架,并绘M 图 解:(1)此刚架具有一个独立转角Z 1和一个独立线位移Z 2。
在结点C 加入一个附加刚臂和附加支杆,便得到图(b)所示的基本结构。
(2)建立位移法方程01212111=++P R Z r Z r 02222121=++P R Z r Z r (3)求各系数和自由项i i i r 73411=+=, i r r 5.12112-==1615434122222ii i r =+=01=P RkN ql RP 6030832-=--=(4)求未知量i Z 87.201=,i Z 39.972= (5)绘制弯矩图例3.用直接平衡法求刚架的弯矩图。
解:(1)图示刚架有刚结点C 的转角Z 1和结点C 、D 的水平线位移Z 2两个基本未知量。
设Z 1顺时针方向转动,Z 2向右移动。
(2)求各杆杆端弯矩的表达式3421+-=Z Z M CA 3221--=Z Z M AC 13Z M CD = 25.0Z M BD -= (3)建立位移法方程有侧移刚架的位移法方程,有下述两种:Ⅰ.与结点转角Z 1对应的基本方程为结点C 的力矩平衡方程。
∑=0CM , 037021=+-⇒=+Z Z M M CD CAⅡ.与结点线位移Z 2对应的基本方程为横梁CD 的截面平衡方程。
∑=0xF, 0=+D C CA Q Q取立柱CA 为隔离体(图(d)),∑=0A M , 331216262121-+-=---=Z Z ql Z Z Q CA 同样,取立柱DB 为隔离体((e)),∑=0B M , 2212165.0Z Z Q DB =--= 代入截面平衡方程得 03125012133121221=-+-⇒=+-+-Z Z Z Z Z(4)联立方程求未知量 Z 1=0.91 Z 2=9.37(5)求杆端弯矩绘制弯矩图将Z 1、Z 2的值回代杆端弯矩表达式求杆端弯矩作弯矩图。
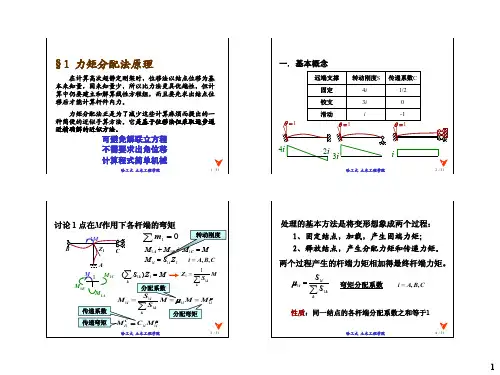






第五章位移法和力矩分配法一、判断题(“对”打√,“错”打)1.位移法和力矩分配法只能用于求超静定结构的内力,不能用于求静定结构的内力。
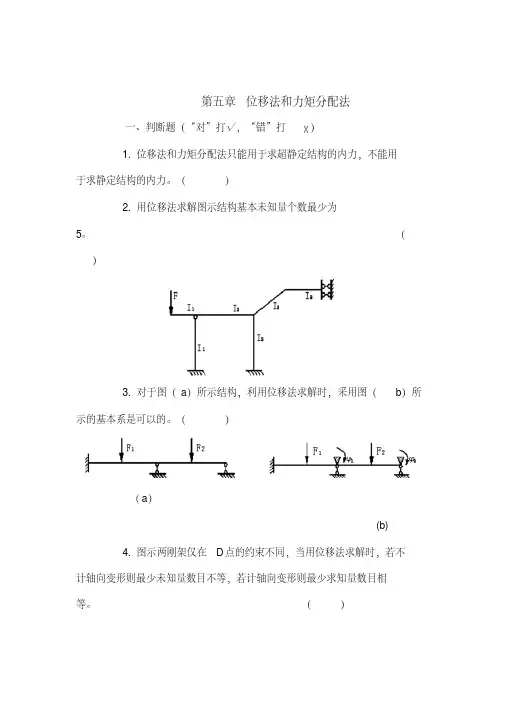
()2.用位移法求解图示结构基本未知量个数最少为5。
()3.对于图(a)所示结构,利用位移法求解时,采用图(b)所示的基本系是可以的。
()(a)(b)4.图示两刚架仅在D点的约束不同,当用位移法求解时,若不计轴向变形则最少未知量数目不等,若计轴向变形则最少求知量数目相等。
()(a)(b)5.图(a)所示结构的M图如图(b)所示。
()(a)(b)6.某刚架用位移法求解时其基本系如图所示,则其MF图中各杆弯矩为0,所以有附加连杆约束力FR1F=0。
( )7.图a结构用位移法计算的基本系如图b,则其2图如图c所示。
()(a) (b)(c)8.图示连续梁在荷载作用下各结点转角的数值大小排序为A>B>C> D. ( )9.图示两结构(EI均相同)中MA相等。
()(a)(b)10.下列两结构中MA相等。
()(a)(b)11.图示结构结点无水平位移且柱子无弯矩。
()12.图示结构下列结论都是正确的:. ( )13.用位移法计算图示结构,取结点B的转角为未知量,则. ( )14.图a对称结构(各杆刚度均为EI)可以简化为图b结构(各杆刚度均为EI)计算。
()(a)(b)15.图a对称结构可以简化为图b结构计算(各杆刚度不变)。
()(a)(b)16.图a对称结构可以简化为图b结构计算。
()(a) (b)17.图(a)所示对称结构,利用对称性简化可得计算简图,如图(b)所示。
()(a) (b) 18.图示结构中有c点水平位移和BE杆B点弯矩()19.图示结构的弯矩图与是否有AB杆和BC杆无关。
()20.用力矩分配法计算图示结构,则分配系数μCD=,传递系数。
()21.根据力矩分配法,图示结构最后弯矩有关系:()22.图a所示连续梁当线刚度i2?i1时,可简化为图b结构按力矩分配法计算。
第五章位移法和力矩分配法一、判断题(“对”打√,“错”打)1.位移法和力矩分配法只能用于求超静定结构的内力,不能用于求静定结构的内力。
()2.用位移法求解图示结构基本未知量个数最少为5。
()3.对于图(a)所示结构,利用位移法求解时,采用图(b)所示的基本系是可以的。
()(a)(b)4.图示两刚架仅在D点的约束不同,当用位移法求解时,若不计轴向变形则最少未知量数目不等,若计轴向变形则最少求知量数目相等。
()(a)(b)5.图(a)所示结构的M图如图(b)所示。
()(a)(b)6.某刚架用位移法求解时其基本系如图所示,则其MF图中各杆弯矩为0,所以有附加连杆约束力FR1F=0。
( )7.图a结构用位移法计算的基本系如图b,则其2图如图c所示。
()(a) (b)(c)8.图示连续梁在荷载作用下各结点转角的数值大小排序为A>B>C> D. ( )9.图示两结构(EI均相同)中MA相等。
()(a)(b)10.下列两结构中MA相等。
()(a)(b)11.图示结构结点无水平位移且柱子无弯矩。
()12.图示结构下列结论都是正确的:. ( )13.用位移法计算图示结构,取结点B的转角为未知量,则. ( )14.图a对称结构(各杆刚度均为EI)可以简化为图b结构(各杆刚度均为EI)计算。
()(a)(b)15.图a对称结构可以简化为图b结构计算(各杆刚度不变)。
()(a)(b)16.图a对称结构可以简化为图b结构计算。
()(a) (b)17.图(a)所示对称结构,利用对称性简化可得计算简图,如图(b)所示。
()(a) (b)18.图示结构中有c点水平位移和BE杆B点弯矩()19.图示结构的弯矩图与是否有AB杆和BC杆无关。
()20.用力矩分配法计算图示结构,则分配系数μCD=,传递系数。
()21.根据力矩分配法,图示结构最后弯矩有关系:()22.图a所示连续梁当线刚度i2»i1时,可简化为图b结构按力矩分配法计算。
()(a)(b)(b)23.图示连续梁发生支座移动如图所示,用力矩分配法计算时结点C的不平衡力矩为零。
()24.图a所示结构可简化为图b结构,用力矩分配法计算。
()(a)(b)三、填空题1.用位移法求图示桁架受对称荷载时,基本未知量个数最少为个。
2.图示结构用位移法求解时,基本未知量个数最少为个。
3.图示单跨梁当A支座有垂直向下单位位移时,MAB= 。
当支座A有垂直于AB的向右下方的单位位移时,MAB= 。
当支座A在水平方向有单位位移时,MAB= 。
4.根据互等定理知道位移法典型方程中的副系数kij=kji,该互等定理可由互等定理导出。
5.若如图示刚架在mB的作用下,B结点产生单位转角。
则mB= 。
(各杆杆长l,刚度为EI)6.对图示结构用位移法求解时,其典型方程一般形式为,其中系数项k11= ,自由项FR1F= 。
7.某结构用位移法求解时,基本系如图所示,则典型方程中的系数k11= ,k12= ,k21= ,k22= ,自由项FR1F= ,FR2F= 。
8.图示结构,EI=常数,已知结点C的水平线位移为,则结点B的角位移B= ,转向为。
(填顺时针或逆时针)9.图示结构,EI=常数,已知结点D的转角,则MDB= ,且侧受拉。
MCD= ,侧受拉。
10.欲使图a和图b中的MB=MB′,则。
11.图示结构A点的弯矩MA= 。
12.利用位移法判断结点A的转角A的转向为。
13.已如图示结构中,则C点水平位移△c=。
14.利用位移法概念求图示结构支座反力FRD= 。
15.图示结构用位移法计算,取结点B的水平位移△1为未知量,则系数k11= 。
16.图示为一连续梁的位移法基本系,则系数k12= , k22= 。
17.图示对称刚架受对称荷载,由位移法可知,MCB= kN·m ,MAB=kN·m.18.图示结构,FQCB= ,FQBE= 。
19.图示结构,MCB= ,侧受拉,MBC= 。
20.图示结构,根据结构和荷载特点分析得FNCB= ,FQCB= 。
21.力矩分配法中,传递系数表示当杆件近端有转角时,与的比值,它与杆件远端的有关。
22.图示结构用力矩分配法计算时,A点的不平衡力矩m= 。
23.用力矩分配法计算图示结构,则分配系数μAB= ,传递系数CAC= 。
24.图示结构用力矩分配法求解时,其结点不平衡力矩mk= .25.图示结构的弯矩MBA= ,MBC= 。
(顺时针为正)26.用力矩分配法计算图示刚架,则分配系数μBA= ,传递系数CBA= 。
(各杆l,EI相同)27.力矩分配法与位移法在消去附加刚臂作用的做法上的不同是:位移法通过满足典型方程使各刚架上反力矩为零,而力矩分配法则是。
一、是非题1、×.位移法取结点位移为基本未知量、附加约束的结构为基本结构,所以也可以用于求静定结构内力,力矩分配法亦类似,但它只可求解无结点线位移的静定结构。
力法须解除多余约束,故不可用于求静定结构内力。
2、×.铰上方的刚结点转角可不取未知量,该题基本未知量数最少为3个(一个线位移、两个角位移)。
3、√.是可以的,但未知量数不是最少的。
矩阵位移法电算中就是这样处理的。
4、√.不计轴向变形基本未知量为(a)4个、(b)3个,计轴向变形均为6个。
5、√.中间的铰无线位移并将结构分为三个部分,它们之间无力矩的传递,可独立画出各自的弯矩图。
6、×.根据截面剪力平衡条件可知。
7、√.注意此时斜杆只有刚体位移无弯矩。
8、√.可根据下列步骤作定性分析:(1)草绘弯矩图和挠曲线图,(2)按超静定结构求位移的方法,取三跨简支梁为静定基本系,(3)分别建立虚力状态计算各跨简支梁两端转角,根据图乘法分析可比较出各支座处转角的大小。
9、√.按力矩分配法计算,两结构的分配系数、传递系数和固端弯矩均相同,故可得出结论。
用位移法分析也可以得出该结论。
10、√. 两结构相对线刚度相同, 分配系数、传递系数和结点不平衡力矩均相同。
11、√. 此结构因水平杆,故刚结点无转角,又若有结点水平线位移,则横梁在水平方向无法平衡,故也无结点水平位移,所以柱子无弯矩。
12、√. 因BC杆,故;若,则ABC杆水平方向无法平衡,故;由于以上两点,BD杆无弯矩;AB 杆相当于B端固定A端铰支,故有。
13、√. 该结构无结点线位移.位移法固定状态下,两杆B端抗弯劲度为,故得。
14、×.因荷载反对称,故在半结构中,原来位于对称轴上的杆的刚度应取为。
15、√.对称结构受对称荷载作用,位于对称轴上两刚结点只能上下移动,但受两斜杆支撑又不能上下移动,故相当于固定。
16、√.对无支座的平衡体,可假设某点相对不动(即固定),对该结构设最下面结点相对固定,其半结构即图(b).17、√.因对称,两刚结点处无转角和水平位移,不仅如此,竖杆任一点也无转角、无水平位移和无弯矩。
简化后的半结构在两刚结处位移条件与原结构相同,故两横梁弯矩不变。
18、×.根据ABCD水平方向平衡可知,E点处无水平约束力,故,但是FEG部分不对称,E点有水平位移要引起C点水平位移。
19、√.因结构对称受对称荷载,B结点无转角和无位移,只有水平杆有弯矩,去掉两斜杆后,以上状态不变。
20、√.结构中D点无转动和移动,可视CD杆为两端固定梁来考虑(当C结点转动时)。
21、×. A端向B端的传递系数,只有当B端固定无转动时才等于,而现在B端为弹性的,故不成立。
22、√.根据条件,第一跨相当于两端固定梁,可求出右端弯矩为,其他部分可简化为图(b)计算。
23、√.力矩分配法固定状态下,BC杆为两端固定梁,求出支座位移作用下的固端弯矩即可叠加出不平衡力矩。
24、√.左边F简化为结点外力偶,右边F简化为杆端外力偶,简化去掉的杆的弯矩按静定法求出。
二、选择题1、B. 左边铰上刚结点转角可不取为未知量,右边铰连接的刚结点转角要取为未知量。
2、C. 其他三图结构均有结点线位移。
3、D. 图A结点无转角,若有水平线位移,则横梁在水平方向无法平衡;图B由对称性,可知无水平线位移;图D结构中间的两刚结点有线位移,独立线位移1个。
4、C. 组合结点铰端转角不是基本未知量。
5、A. 结点A无线位移,又假设A点不能转动,则B、C点也不能转动和位移,故只有一个基本未知量。
6、C. 因为必须。
7、A. BA杆B端抗弯劲度为0。
8、C. A点向右,B点向上,AB杆转的角度为;AB杆两端垂直杆轴的相对位移为杆长乘转角,即;杆件按两端固定梁计算得杆端弯矩。
9、B. 根据位移法,要,必须自由项,即可求得。
10、C. 左边四个竖杆对的贡献均为;右边四杆中除右下角的杆子外,对的贡献均为。
11、D. 结点上集中力F要考虑。
12、D. 应等于各杆A端抗弯劲度之和,右横梁抗弯劲度为0。
13、A. 应等于各杆刚结点处的固端弯矩之和,右边的集中力可简化成结点集中力偶6kNm。
14、A. 图b结构A结点无线位移,受结点集中力作用时结构无弯矩。
图a结构则非。
15、B. 由ABCE部分水平方向平衡条件知E点无水平约束力,故此部分为对称受力状态,故有。
其他三个均不为0。
16、C. 不引起;F可视为反对称荷载,由此求出底部两水平反力为,则可求出。
17、C. 由对称知,则可求.B点无线位移,则A点的弯矩为B点的一半.故有。
18、D. 因为图D结构有侧移。
19、A. 注意杆AD的抗弯劲度为0,AB杆与两端固定梁一样。
20、C. 注意分配系数的计算式并非它的定义。
21、B. 分配系数、传递系数是结构固有的,与荷载无关。
22、A. 水平杆无弯矩,又刚结点无线位移故按传到固定端。
23、C. 用力矩分配法分析,图b结构两杆分配系数和传递系数均相同,故有和截面弯矩相等;其他等式均不成立。
24、A. 按力矩分配法概念,作用结点C的外力偶矩全部分配给CD杆C端(分配系数)。
三、填空题1、6. 由于结构约束不对称,虽然受力对称但位移不对称,有四个水平位移和3个竖向位移未知量,考虑到结构最终保持对称的变形状态。
A ,C两点竖向位移相同,故基本未知量为6个。
2、1. 若将下面一个刚结点加刚臂约束住,则上面一个刚结点就不能转动和移动。
3、 0,,. A支座向下移动,AB杆向下平移;A支座垂直于杆轴移动时,可按一端固定,另一端铰支处理;A支座向右水平移动,B点向上,AB杆转过的角度为 ,引起两端相对位移为,进而再按一端固定一端铰支计算固端弯矩。
4、反力, 虚功。
5、. 应等于各杆B端抗弯劲度之和。
6、, , 0. 该结构只有一个水平线位移未知量。
7、, , , , 0, . 注意在作用下,斜杆为刚体平移,无弯矩。
8、, 顺时针. 建立一个位移法方程:即可求出(即)9、, 右, , 下. 可按计算,简单地也可按单跨梁分别计算:,也可按两端固定梁AD,受及F作用的结果相叠加得到。