结构力学题库第九章 力矩分配法习题解答
- 格式:doc
- 大小:796.50 KB
- 文档页数:15

力矩分配法例题及详解1. 引言嘿,大家好!今天我们来聊聊一个听起来有点复杂,但其实非常实用的概念——力矩分配法。
首先,别被这个名字吓到了,力矩听起来就像是一种神秘的力量,但其实它和我们日常生活息息相关,像是开门、搬家具,甚至是扔飞盘,都能用上哦!接下来,我们就从一些基础概念说起,慢慢让这个看似高深的东西变得简单易懂。
2. 力矩的基本概念2.1 力矩是什么?那么,力矩到底是什么呢?简单来说,力矩就是一个力在某个点上产生的转动效果。
你可以想象一下,你在转动一个门把手。
门把手离门铰链越远,你转动的效果就越明显。
也就是说,力矩=力×距离,这里的距离就是你施力的点到铰链的距离。
明白了吗?就像你拉开冰箱门的时候,越往边上拉,门就开得越大,没错吧?2.2 力矩的方向力矩不仅仅有大小,还有方向哦!通常我们用“顺时针”和“逆时针”来描述。
比如你在玩转盘游戏时,顺时针转动力矩可以让转盘指向某个数字,而逆时针则可能指向另一个数字。
方向的不同,有时候就能让你赢得游戏,没错,力矩在生活中可真是无处不在。
3. 力矩分配法的应用3.1 生活中的例子好了,咱们说了这么多,来点实际的例子吧!想象一下你和朋友们一起搬一个大沙发。
沙发很重,大家都想用力去推,但如果每个人都往同一个方向使劲,结果可能就是沙发半天也动不了。
这时候,你就需要用到力矩分配法!大家可以分成两组,一组在沙发一端推,另一组在另一端拉,利用力矩的原理,沙发就能轻松移动,简单又有效。
3.2 力矩分配法的步骤说到这儿,大家肯定好奇,具体怎么分配力矩呢?首先,得找到一个合适的支点。
然后,大家围绕这个支点站好,确定每个人施力的方向和位置。
最后,再开始施力,看看大家的默契如何!这个过程就像打篮球一样,配合得当才能得分;而力矩分配法就能让你在各种“搬运”中轻松获胜。
4. 小结最后,总结一下今天的内容。
力矩分配法听上去复杂,但其实它的原理就是利用每个人的力量,合理分配到不同的位置,达到最佳效果。


力矩分配法课后习题答案力矩分配法课后习题答案力矩分配法是一种常用的力学分析方法,用于计算物体上的力矩分布。
在工程学和物理学中,力矩分配法被广泛应用于解决各种问题,包括结构力学、机械设计和静力学等。
下面将通过几个具体的习题来介绍和解答力矩分配法的应用。
习题1:一个均匀的杆AB长为L,质量为m,放置在两个支点A和B上。
支点A距离杆的左端点的距离为a,支点B距离杆的右端点的距离为b。
求支点A和B所受的力。
解答:根据力矩分配法,我们可以先计算出杆的重心位置。
重心位置可以通过以下公式计算得出:x = (m1 * x1 + m2 * x2) / (m1 + m2)其中,m1和m2分别是杆上两个质点的质量,x1和x2分别是这两个质点的位置。
在本题中,我们可以将杆分为两个部分:左侧的部分质量为m1,右侧的部分质量为m2。
左侧部分的质心位置为a/2,右侧部分的质心位置为L - b/2。
代入公式,我们可以得到:x = (m1 * a/2 + m2 * (L - b/2)) / (m1 + m2)接下来,我们可以计算出支点A和B所受的力。
根据平衡条件,支点A所受的力的大小应该等于杆上重心位置处的力矩与杆的重力矩之和。
支点B所受的力的大小应该等于杆上重心位置处的力矩与杆的重力矩之差。
因此,我们可以得到以下两个方程:Fa = (m1 + m2) * g - (m1 * a/2 + m2 * (L - b/2)) * gFb = (m1 + m2) * g + (m1 * a/2 + m2 * (L - b/2)) * g其中,g是重力加速度。
通过解这两个方程,我们可以求解出支点A和B所受的力。
习题2:一个悬挂在墙上的杆,杆的质量为m,长度为L。
杆的左端点与墙壁接触,右端点悬挂在墙上的钩子上。
求杆的重心位置和墙壁对杆的支持力。
解答:首先,我们可以计算出杆的重心位置。
由于杆是均匀的,重心位置就在杆的中点。
因此,杆的重心位置为L/2。




力矩分配法练习题答案第 1 题力 矩 分 配 法 计 算 得 出 的 结 果 :A. 一 定 是 近 似 解 ;B. 不 是 精 确 解 ;C. 是 精 确 解 ;D. 可 能 为 近 似 解 , 也 可 能 是 精 确 解 。
()答案( D )第 2 题在力 矩 分 配 法 中 , 刚 结 点 处 各 杆 端 力 矩 分 配 系 数 与 该 杆 端 转 动 刚 度 ( 或 劲 度 系 数 ) 的 关 系 为 :A. 前 者 与 后 者 的 绝 对 值 有 关 ;B. 二 者 无 关 ;C. 成 反 比 ;D. 成 正 比 。
()答案( D )第 3 题在 力 矩 分 配 法 的 计 算 中 , 当 放 松 某 个 结 点 时 , 其 余 结 点 所 处 状 态 为 :A. 全 部 放 松 ;B. 必 须 全 部 锁 紧 ;C.. 相 邻 结 点 放 松 ;D 相 邻 结 点 锁 紧 。
( )答案( D )第 4 题用 力 矩 分 配 法 计 算 时 , 放 松 结 点 的 顺 序 :A. 对 计 算 和 计 算 结 果 无 影 响 ;B. 对 计 算 和 计 算 结 果 有 影 响 ;C.. 对 计 算 无 影 响 ;D . 对 计 算 有 影 响 , 而 对 计 算 结 果 无 影 响 。
()答案( D )第 5 题图 a所 示 结 构 的 弯 矩 分 布 形 状 如 图 b 所 示 。
()( )b答案 ( X )第 6 题图 示 结 构 , 各 杆 i = 常 数 , 欲 使 A 结 点 产 生 单 位 顺 时 针 转 角 θA =1,须 在 A 结 点 施 加 的 外 力 偶 为 数 -8i 。
( )A答案 ( X )第 7 题力 矩 分 配 法 中 的 传 递 弯 矩 等 于 :A . 固 端 弯 矩 ;B . 分 配 弯 矩 乘 以 传 递 系 数 ;C . . 固 端 弯 矩 乘 以 传 递 系 数 ;D . 不 平 衡 力 矩 乘 以 传 递 系 数 。

9.1 复习笔记【知识框架】【重点难点归纳】一、力矩分配法(见表9-1-1) ★★★★图9-1-1二、无剪力分配法(见表9-1-2) ★★表9-1-2 无剪力分配法表9-1-3 剪力分配法9.2 课后习题详解复习思考题1.什么是转动刚度?什么是分配系数?为什么一刚结点处各杆端的分配系数之和等于1?答:(1)转动刚度的定义杆端的转动刚度是指当杆件的近端转动单位角时,在该近端产生的弯矩。
(2)分配系数的定义分配系数是指结点某一杆端的劲度系数与该结点处所有杆端的劲度系数的比值。
(3)刚结点处各杆端的分配系数之和等于1的原因:因为分配系数的计算公式,在刚节点处各杆端分配系数之和应为1ijij n ijj S Sμ==∑111n ij j ij n ijj SSμ====∑∑2.单跨超静定梁的劲度系数和传递系数与杆件的线刚度有何关系?答:单跨超静定梁的劲度系数不仅与杆件线刚度i=EI/l相关,而且与杆件另一端(又称远端)的支承情况有关;传递系数与杆件的线刚度无关,只与远端支承形式有关。
3.图9-2-1所示三个单跨梁,仅B端约束不同。
它们的劲度系数S AB和传递系数C AB 是否相同,为什么?图9-2-1答:不考虑杆件轴向变形,(a)、(b)、(c)三个单跨梁的劲度系数均相同,即S AB=4i,其中i为杆件的线刚度;(a)、(b)、(c)三个图的传递系数均相同,即C AB=0.5。
因为虽然B端约束表面上形式各异,但在不考虑杆件轴向变形的条件下,(a)、(b)、(c)三个单跨梁在B端的最终约束效果上均可以当成固定端来处理。
若考虑杆件轴向变形,(a)、(c)的劲度系数相同,(b)远端可在水平向自由收缩,A端转到相同的转角需要的力更小,因此劲度系数略小于(a)、(c)。
4.什么是不平衡力矩?如何计算不平衡力矩?为什么要将它反号才能进行分配?答:(1)不平衡力矩的定义不平衡力矩是指在附加约束结点处各固端弯矩所不能平衡的差额。

9-7试求图示等截面单跨梁的极限荷载。
梁的截面为矩形b ×h=5 cm×20 cm,s σ=235 Mpa 。
解 根据弯矩图形状,很容易判断,形成机构说,塑性铰出现在B 、D 两点,故()Pu u u 22u e Pu 11335cm 20cm 235MPa 4704kN F l M M M bh F l l l lσ-=⨯⨯====习题9-7图9-8试求图示等截面单跨梁的极限荷载。
解:梁变成机构时,任意截面的弯矩为3u23u u 11()66d ()110d 6231166M x qlx qx M l M x ql qx x x l M ql q M q l =--=-===--=9-9试求图示等截面超静定梁的极限荷载。
解: 第一跨变成机构时,()()11Pu u Pu u 181.56m 2(kN)49F M F M ⨯⨯==第二跨变成机构时,()()22Pu u Pu u 16m 1.5(kN)4F M F M ⨯⨯==极限弯矩为()2Pu Pu u (kN)F F M ==习题9-8图9-10试求图示等截面连续梁的极限弯矩。
解: 第一跨变成机构时,()211u u 1320kN/m 6m 60kNm 82M M ⨯⨯==()()()()()()()()()()2u11u u 211111u u u uu 1122u u 212u 11()22d ()1110d 221111112222211822361.92kNm 2xM x qlx qx M lM M x ql qx M x l x l qlM M M M ql l q l l M ql ql l ql M M ql ql M ql =--=--==-⎛⎫⎛⎫⎛⎫=----- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-+-== 第二跨变成机构时,()()()222u u 1120kN/m 6m 40kN 6m 275kNm 84M M ⨯⨯+⨯⨯==第三跨变成机构时,()()33u u 1332080kN 8m kNm 106.7kNm 423M M ⨯⨯=== 极限弯矩为()3u u 106.7kNm M M ==9-11试求图示阶形柱的极限荷载。
力矩分配法试题及答案一、单项选择题1. 力矩分配法中,分配系数的计算公式为()。
A. 分配系数 = 杆端弯矩 / 杆端剪力B. 分配系数 = 杆端剪力 / 杆端弯矩C. 分配系数 = 杆端弯矩 / 杆端反力D. 分配系数 = 杆端反力 / 杆端弯矩答案:D2. 在力矩分配法中,传递系数的计算公式为()。
A. 传递系数 = 杆端反力 / 杆端弯矩B. 传递系数 = 杆端弯矩 / 杆端反力C. 传递系数 = 杆端弯矩 / 杆端剪力D. 传递系数 = 杆端剪力 / 杆端弯矩答案:B3. 力矩分配法适用于()结构。
A. 刚架B. 桁架C. 连续梁D. 所有结构答案:C4. 力矩分配法中,分配力矩的计算公式为()。
A. 分配力矩 = 分配系数 ×杆端弯矩B. 分配力矩 = 分配系数 ×杆端反力C. 分配力矩 = 杆端弯矩 ×分配系数D. 分配力矩 = 杆端反力 ×分配系数答案:A5. 力矩分配法中,传递力矩的计算公式为()。
A. 传递力矩 = 传递系数 ×分配力矩B. 传递力矩 = 分配力矩 ×传递系数C. 传递力矩 = 传递系数 ×杆端弯矩D. 传递力矩 = 杆端弯矩 ×传递系数答案:B二、多项选择题1. 力矩分配法中,分配系数的计算需要考虑的因素包括()。
A. 杆件的刚度B. 杆件的长度C. 杆件的截面特性D. 杆件的连接方式答案:A2. 力矩分配法中,传递系数的计算需要考虑的因素包括()。
A. 杆件的刚度B. 杆件的长度C. 杆件的截面特性D. 杆件的连接方式答案:A3. 力矩分配法适用于以下哪些结构()。
A. 刚架B. 桁架C. 连续梁D. 悬臂梁答案:C4. 力矩分配法中,分配力矩和传递力矩的计算需要考虑的因素包括()。
A. 分配系数B. 传递系数C. 杆端弯矩D. 杆端反力答案:A, B, C5. 力矩分配法中,以下哪些因素会影响结构的内力分布()。
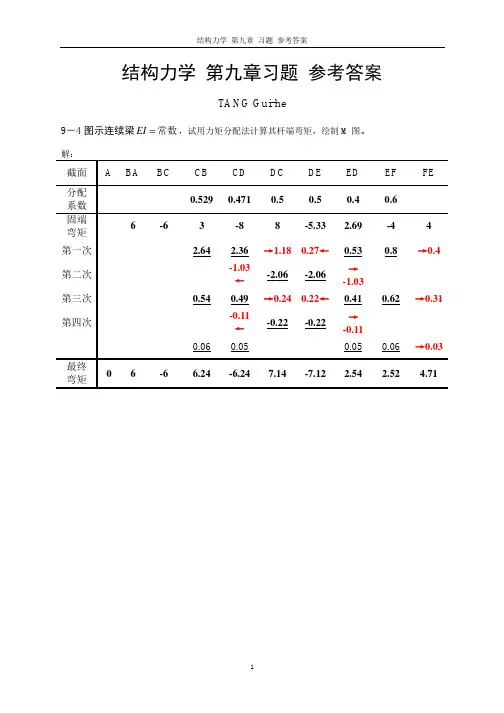
1、清华5-6 试用力矩分配法计算图示连续梁,并画其弯矩图和剪力图。
C清华V图M(kN解:(1)计算分配系数:320.632440.4324BABABA BCBCBCBA BCs is s i is is s i iμμ⨯===+⨯+⨯⨯===+⨯+⨯(2)计算固端弯矩:固端弯矩仅由非结点荷载产生,结点外力偶不引起固端弯矩,结点外力偶逆时针为正直接进行分配。
3360667.51616FABFBAMPlM=⨯⨯===⋅kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
(5)根据弯矩图作剪力图如图所示。
0153027.60153032.63517.58.756AB BA AB AB AB BA BA BA BC CB BC CB M M V V l M M V V l M M V V l ++=-=-=++=-=--=+--==-=-=5kN 5kN kN2、利用力矩分配法计算连续梁,并画其弯矩图和剪力图。
4m1m2m2m原结构简化结构·解:(1)计算分配系数:,4,34BA BC BA BC EIi i i S i S i =====令 430.4290.5714343BC BA BA BC BA BC BA BC s s iis s i is s i iμμ======++++(2)计算固端弯矩:CD 杆段剪力和弯矩是静定的,利用截面法将外伸段从C 处切开,让剪力直接通过支承链杆传给地基,而弯矩暴露成为BC 段的外力偶矩,将在远端引起B 、C 固端弯矩。
22204101088154102020828F FAB BA F F BCCB Pl M M ql m M M ⨯=-=-=-⋅⋅⨯=-+=-+=-⋅=⋅kN m,=kN m kN m,kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
第9章超静定结构的实用计算方法与概念分析习题答案9-1 试说出何为杆端转动刚度、弯矩分配系数和传递系数,为什么弯矩分配法一般只能用于无结点线位移的梁和刚架计算。
9-2 试用弯矩分配法计算图示梁和刚架,作出M 图,并求刚结点B 的转角φB 。
解:设EI=6,则5.1,1==BC AB i i53.05.13145.1347.05.131414=⨯+⨯⨯==⨯+⨯⨯=BCBA μμ结点 A BC 杆端 AB BA BC 分配系数 固端 0.47 0.53 绞支 固端弯矩 -60 60 -30 0 分配传递 -7.05 -14.1 -15.9 0 最后弯矩-67.0545.9-45.9()()()逆时针方向215.216005.6721609.4522131m KN EIEI m M m M i AB AB BA BA B ⋅-=⎥⎦⎤⎢⎣⎡+---=⎥⎦⎤⎢⎣⎡---=θ(b)解:设EI=9,则3,31,1====BE BD BC AB i i i i6m3m 3m2m6m2m12.0141333331316.0141333331436.01413333333=⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==BC BA BE BD μμμμ结点 A BC 杆端 AB BA BC BD BE 分配系数 固端 0.16 0.12 0.36 0.36 绞支 固端弯矩 0 0 0 45 -90 0 分配传递 3.6 7.2 5.4 16.2 16.2 0 最后弯矩3.67.25.461.2-73.8()()()顺时针方向22.1606.32102.732131m KN EIEI m M m M i AB AB BA BA B ⋅=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡---=θ9-3 试用弯矩分配法计算图示刚架,并作出M 图。
(a)解:B为角位移节点设EI=8,则1==BC AB i i ,5.0==BC BA μμ 固端弯矩()m KN l b l Pab M BA ⋅=⨯⨯⨯⨯=+=4882124432222 m KN l M BC ⋅-=⋅+-=582621892 结点力偶直接分配时不变号结点 A BC 杆端 AB BA BC 分配系数 铰接 0.5 0.5 固端弯矩 0 48 -58 12 分配传递50 50 55124m 4m8m2m最后弯矩 0103 -3 12(b)解:存在B 、C 角位移结点 设EI=6,则1===CD BC AB i i i 73741413145.0141414==⨯+⨯⨯==⨯+⨯⨯==BC CB BC BA μμμμ固端弯矩: mKN M M M m KN M m KN M CDCB BC BA AB ⋅-=⨯+⨯-===⋅-=⋅-=14021808640080802结点 A BC杆端 AB BA BC CB CD 分配系数 固结 0.5 0.5 4/7 3/7 固端弯矩-80 80 0 0 -140 分配传递-20 -40 -40 -20 47.5 91.4 68.6 -11.4 -22.8 -22.8 -11.4 3.25 6.5 4.9 -0.82-1.63-1.63-0.820.6 0.45 最后弯矩-112.2215.57-15.4866.28-66.052m 6m2m2m2m 6m(c)解:B 、C 为角位移结点51411,5441454414,51411=+==+==+==+=CD CBBC BA μμμμ固端弯矩:mKN M mKN M mKN M mKN M mKN M mKN M DC CD CB BC BA AB ⋅-=⨯-=⋅-=⨯-=⋅=⨯=⋅-=⨯-=⋅=⨯=⋅=⨯=10065242003524501252450125241283424646424222222结点 A BCD 杆端 AB BA BC CB CD 滑动 分配系数 滑动 0.2 0.8 0.8 0.2 -100固端弯矩64 128 -50 50 -200 分配传递15.6 -15.6 -62.4 -31.272.48 144.96 36.24 -36.24 14.5 -14.5 -58 -29 11.6 23.2 5.8 -5.8 2.32-2.32-9.28-4.643.7 0.93 -0.93 最后弯矩96.4295.58-95.6157.02-157.03-142.974m5m5m3m96.42(d) 解:11313141413114131414145.0141414=⨯+⨯+⨯⨯===⨯+⨯+⨯⨯===⨯+⨯⨯=DBDE DC CD CA μμμμμ 固端弯矩:mKN M mKN M ED DE ⋅=⋅-=⨯-=383812422结点 A CD E 杆端 AC CA CD DC DB DE ED 分配系数 固结 0.5 0.5 4/11 3/11 4/11 固结固端弯矩0 0 0 0 0 -2.67 2.67 分配传递-5-10 -10 -546/33 92/33 69/33 92/33 46/33 -0.35 - 23/33- 23/33-0.350.127 0.096 0.127 0.064 最后弯矩-5.35-10.7-9.3-2.442.190.254.12(e)4m6m4m4m4m解:当D 发生单位转角时:()()2414-=⨯⨯=m EI K Y C 则())假设12(441==⨯=-m EI EIM DC73,74,3716,379,371216,12,16,9,12=====∴=====∴EB ED DE DA DC DE EB DE DA DC S S S S S μμμμμ 结点 D EB 杆端 DC DA DE ED EB BE 分配系数 12/37 9/37 16/37 4/7 3/7 固结 固端弯矩0 0 -9 9 0 0 分配传递-2.57 -5.14 -3.86 -1.93 3.75 2.81 5 -2.5 -0.72 -1.43 -1.07 -0.54 0.230.18 0.31 0.16 最后弯矩3.982.99-6.985-5-2.47(f)解:截取对称结构为研究对象。
1、清华5-6 试用力矩分配法计算图示连续梁,并画其弯矩图和剪力图。
C清华V图M(kN解:(1)计算分配系数:320.632440.4324BABABA BCBCBCBA BCs is s i is is s i iμμ⨯===+⨯+⨯⨯===+⨯+⨯(2)计算固端弯矩:固端弯矩仅由非结点荷载产生,结点外力偶不引起固端弯矩,结点外力偶逆时针为正直接进行分配。
3360667.51616FABFBAMPlM=⨯⨯===⋅kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
(5)根据弯矩图作剪力图如图所示。
0153027.60153032.63517.58.756AB BA AB AB AB BA BA BA BC CB BC CB M M V V l M M V V l M M V V l ++=-=-=++=-=--=+--==-=-=5kN 5kN kN2、利用力矩分配法计算连续梁,并画其弯矩图和剪力图。
4m1m2m2m原结构简化结构·解:(1)计算分配系数:,4,34BA BC BA BC EIi i i S i S i =====令 430.4290.5714343BC BA BA BC BA BC BA BC s s iis s i is s i iμμ======++++(2)计算固端弯矩:CD 杆段剪力和弯矩是静定的,利用截面法将外伸段从C 处切开,让剪力直接通过支承链杆传给地基,而弯矩暴露成为BC 段的外力偶矩,将在远端引起B 、C 固端弯矩。
22204101088154102020828F FAB BA F F BCCB Pl M M ql m M M ⨯=-=-=-⋅⋅⨯=-+=-+=-⋅=⋅kN m,=kN m kN m,kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
(5)根据弯矩图作剪力图如图所示。
00207.1415.717.8624207.1415.7112.142415415.712028.932415415.712031.0724AB BA AB AB AB BA BA BA BC CBBC BC BC CB CB CB M M V V l M M V V l M M V V l M M V V l +-+=-=-=+-+=-=--=-+⨯-+=-=-=+⨯-+=-=--=-kN kNkNkN3、9-2a 利用力矩分配法计算连续梁,并画其弯矩图。
(2)计算固端弯矩:固端弯矩仅由非结点荷载产生。
22222222224524454240,20661581080,8012123340645,1616FFABBAF FBC CB F F CDDC Pab Pba MMl l ql M M Pl M M ⨯⨯⨯⨯=-=-=-⋅==-=⋅⨯=-=-+=-⋅=⋅⨯⨯=-=-=-⋅=kN m kN mkN m kN m kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
4、9-3c 利用力矩分配法计算刚架,并画其弯矩图。
40.75 1.5342,43628420.42330.6231.534332846230.63220.432BA BC BA BABA BC BC BC BA BC CB CD CB CBCB CD CD CD CB CD EI B EI EI EI EIS S s s s s s s C EI EI EI EIS S s s s s s s μμμμ==⨯===⨯=====++===++=⨯===⨯=====++===++令结点:结点:,解:(1)计算分配系数:题9-2aM 图(kN·m)(d)7.5(kN ·m)3m4m1m3m(·m解:(1)计算分配系数:22 1.53 1.53,32,4246623,2,230.37533220.2533230.375332BA BC BE BA BC BE BA BA BA BC BE BC BC BA BC BE BE BC BA BC BE EI EI EIS EI S EI S EI EI S S S s s s S s s s S s s s S μμμ=⨯===⨯===⨯=========++++===++++===++++令则,(2)计算固端弯矩:刚结点处力偶不引起固端弯矩,结点外力偶逆时针为正直接进行分配。
CD 杆段剪力和弯矩是静定的,利用截面法将外伸段从C 处切开,让剪力直接通过支承链杆传给地基,而弯矩暴露成为BC 段的外力偶矩,将在远端引起B 、C 固端弯矩。
225433406100104088162162100F FFABBABC F F FABEB BE ql Pl m MM M M M M ⨯⨯⨯===⋅=-+=-+=-⋅=⋅==⋅,kN m kN m,kN m kN m(3)分配与传递,计算如图所示。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
9-3d 利用力矩分配法计算刚架,并画其弯矩图。
(a )2m4m 4m-1(d)(c )(b )解:(1)计算分配系数:4 2.5333,442,4544444,4430.332420.23244324CB CB CG CG CFCF CD CD CB CB CB CG CF CD CG CGCB CG CF CD CF CF CB CG CF CD EI EIS i EI S i EI EI EIS i EI S i EIS EIs s S S EI EI EI EI S EIs s S S EI EI EI EI S EIs s S S EI EI μμμ==⨯===⨯===⨯=======++++++===++++++==+++++0.40.1324CD CD CB CG CF CD EI EI S EIs s S S EI EI EI EIμ=+===++++++(2)计算固端弯矩:AB 杆段剪力和弯矩是静定的,利用截面法将外伸段从B 处切开,让剪力直接通过BE 杆传给地基,而弯矩暴露成为BC 段的外力偶矩,将在远端C 引起固端弯矩。
2220104201028282.545220F FBCCBF FCD DC F FCGGC m ql MM Pl M M M M -⨯=-⋅=+=+=⋅⨯==-=-=-⋅==kN m kN mkN m(3)分配与传递,计算如图所示。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
9-3e 利用力矩分配法计算刚架,并画其弯矩图。
-0.75-18.7521.130.133(d )(c )(b )1m4.5m6m(a )解:(1)计算分配系数: B 刚结点:2223,4,44.53636313BA BC BE BABC BE EI EI EI S EI S EI S EI μμμ=⨯==⨯==⨯====C 刚结点:224,463630.5CB CF CBCF EI EI S EI S EI μμ=⨯==⨯=== (2)计算固端弯矩:CD 杆段剪力和弯矩是静定的,利用截面法将外伸段从B 处切开,让剪力直接通过CF 杆传给地基,而弯矩暴露成为作用于刚结点B 的外力偶矩,将在远端C 不引起固端弯矩。
222211246722467212121212F FBCBCql ql MM=-=-⨯⨯=-⋅==⨯⨯=⋅kN mkN m 无荷载杆无固端弯矩。
(3)分配与传递,计算如图所示。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
9-3h 利用力矩分配法计算刚架,并画其弯矩图。
(c )0.1013.342.32(a )解:(1)计算分配系数: B 刚结点:4,4,440.52BA BC BABC EI EIS EI S EI EIEIμμ=⨯==⨯====C 刚结点:33,4,444440.36434340.27234CD CF CB CFCB CDEI EI EI EI S S EI S EI EIEIEI EI EI EIEI EI μμμ=⨯==⨯==⨯====++==++ (2)计算固端弯矩:222211304403044012121212338046016160FFBAAB FCD F F F BC CB CF ql ql M M Pl M M M M ==⨯⨯=⋅=-=-⨯⨯=-⋅=-=-⨯⨯=-⋅===kN m kN mkN m无荷载杆无固端弯矩。
(3)分配与传递,计算如图所示。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
5、9-4b 利用对称性,采用力矩分配法计算刚架,并画其弯矩图。
8.51-0.03-1.465kN/mq=5kN/m(d )6、9-4d 利用对称性,采用力矩分配法计算刚架,并画其弯矩图。
(e)(b)2224q l --2427、9-9c 利用无剪力分配法计算刚架,并画其弯矩图。
(a )题9-9a(g)((e)(d)-0.04-19.72A解:(1)由于刚架是对称的,因此可将荷载分解为正对称和反对称两部分,如上图(b )、(c )所示。
而正对称结点荷载作用下刚架处于无弯矩状态,原图的弯矩图只考虑反对称荷载作用。
考虑刚架和荷载的对称性,可以取半刚架如(d)所示。
由于(d)图半刚架立柱的剪力是静定的,每一跨都可以化为单跨超静定梁,因此选取如图(e)所示无剪力分配法力学计算模型。
(2)计算分配系数: A 结点:3340.92334110.083341AG AG AG AG AC AG ACAC AC ACAG AC AG AC S i S S i i S i S S i i μμ⨯⎧====⎪++⨯+⎪⎨⎪====⎪++⨯+⎩C 结点:110.073134114334120.863134114110.073134114CA CA CACA CH CE CA CH CE CH CH CH CA CH CE CA CH CE CE CE CECA CH CE CA CH CE S i S S S i i i S i S S S i i i S i S S S i i i μμμ⎧=====⎪+++++⨯+⎪⎪⨯=====⎨+++++⨯+⎪⎪=====⎪+++++⨯+⎩(2)计算固端弯矩:266kN m 2224618kN m22F FAC CA F F CE ECP l M M P l M M ⋅⨯==-=-=-⋅⋅+⨯==-=-=-⋅上上+下()1604120kN m 2F FBC CB M M ==-⨯⨯=-⋅(3)弯矩的分配与传递计算过程如图(f)所示。