直线的点向式方程
- 格式:doc
- 大小:121.50 KB
- 文档页数:4

空间直线方程的五种形式在空间几何学中,直线是一种基本的几何对象,描述了两个点之间的最短路径。
在三维空间中,直线的方程可以用五种不同的形式来表示。
这五种形式分别是点向式、对称式、一般式、参数式和标准式。
本文将对这五种形式进行详细的介绍和比较。
一、点向式点向式表示了直线上的一个点和直线的方向向量。
如果我们知道直线上的一个点P和它的方向向量d,那么直线上的任何一点Q都可以表示为:Q = P + td其中t是一个实数,表示从点P出发,沿着方向向量d走多远到达点Q。
点向式的优点是简单明了,易于理解和计算。
但是,它的缺点是不够精确,因为方向向量d可以有不同的长度和方向,所以同一条直线可以有多种不同的点向式。
二、对称式对称式表示了直线上的一个点和直线的对称轴。
如果我们知道直线上的一个点P和它到直线的距离d,那么直线上的任何一点Q都可以表示为:|PQ| = d其中|PQ|表示点P到点Q的距离。
对称式的优点是可以精确地表示直线的位置,而不受方向向量的影响。
但是,它的缺点是不太方便计算,因为需要计算点到直线的距离。
三、一般式一般式表示了直线的一般方程形式。
如果我们知道直线的方向向量d和一个点Q,那么直线的一般式可以表示为:Ax + By + Cz + D = 0其中A、B、C是方向向量d的三个分量,D是常数项,可以通过点Q的坐标和方向向量d计算得出。
一般式的优点是可以表示任何一条直线,而不受方向向量的限制。
但是,它的缺点是不够直观,不容易理解和计算。
四、参数式参数式表示了直线上的所有点都可以由一个参数t来表示。
如果我们知道直线上的两个点P和Q,那么直线的参数式可以表示为:x = x0 + t(x1 - x0)y = y0 + t(y1 - y0)z = z0 + t(z1 - z0)其中(x0, y0, z0)和(x1, y1, z1)分别是点P和Q的坐标,t是一个实数。
参数式的优点是可以方便地计算直线上的任何一点,而且可以通过改变参数t来遍历整条直线。



三维直线方程的五种形式在数学中,三维直线是指具有三个坐标轴上的点的集合。
三维直线也是建立立体几何体系的基础,因为绝大多数物体都是由直线和曲线组成的。
本文将详细介绍三维直线方程的五种形式。
形式一:点向式点向式是求解三维直线方程最简单的方法之一。
它利用一个点和一个方向向量来表示直线。
不妨设三维空间中的直线为L,点为P,方向向量为V,则点向式可以表示为:L: P + tV其中,t是一个实数。
通过改变t的值,可以获得L上的所有点。
如果只想求得直线上的一个点,则可以取t=0。
形式二:参数式参数式是我们在学习二维平面直线的时候就已经了解的一种方法。
具体来说,参数式是通过一组参数方程来表示直线上的所有点。
设直线 L 的参数方程为x = x_0 + aty = y_0 + btz = z_0 + ct则L可以表示为:L: (x - x_0)/a = (y - y_0)/b = (z - z_0)/c其中,a、b、c均不为零。
参数式可以表示L上的所有点,但需要满足一个限制条件,即a、b、c不能同时为零。
形式三:标准式标准式是指利用两个点来表示直线的方程式。
设L过点A(x1,y1,z1)和点B(x2,y2,z2),则L可以表示为:L: (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1) = (z -z1)/(z2 - z1)标准式可以用来快速确定直线所在的位置。
然而,需要注意的是,标准式只有在点A和点B坐标都已知的情况下才适用。
形式四:一般式一般式是指将参数a、b、c以及点(x0,y0,z0)转换成系数A、B、C、D的式子。
具体来说,L的一般式可以表示成:Ax + By + Cz + D = 0其中,A、B、C、D的计算公式如下:A = y1z2 - y2z1B = z1x2 - z2x1C = x1y2 - x2y1D = -A*x1 - B*y1 - C*z1利用一般式,可以将直线转换为平面,方便后续计算。

空间直线点向式方程和一般方程的相互转化数学中,空间直线的表示方式有很多种,其中最常见的有直线的向式方程和一般方程。
这两种方程之间的相互转化在数学中有着广泛的应用。
本文将从向式方程和一般方程的基本概念、转化方法等方面进行介绍。
一、向式方程的基本概念向式方程是指通过直线上一点和直线的方向向量,来表示直线的方程。
具体来说,若直线L上有点P(x0,y0,z0),且直线的方向向量为a(a1,a2,a3),则直线的向式方程可以表示为:(x-x0)/a1 = (y-y0)/a2 = (z-z0)/a3其中,x、y、z分别表示直线上任意一点的坐标。
二、一般方程的基本概念一般方程是指通过直线上两个不同的点来表示直线的方程。
具体来说,若直线L上有两点P1(x1,y1,z1)和P2(x2,y2,z2),则直线的一般方程可以表示为:(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1)其中,x、y、z分别表示直线上任意一点的坐标。
三、向式方程和一般方程的相互转化在数学中,向式方程和一般方程是可以相互转化的。
具体来说,有以下两种转化方式:1. 从向式方程转化为一般方程若已知直线L的向式方程为:(x-x0)/a1 = (y-y0)/a2 = (z-z0)/a3我们可以通过以下步骤将其转化为一般方程:(1)将向量a化为平面上的两个向量b和c。
具体来说,我们可以任意选取两个向量b和c,使它们与向量a不共线,然后使用向量叉积的方法求出向量n=b×c(其中×表示向量叉积)。
向量n垂直于平面,而既过点P且平行于向量a的直线L,则与平面到点P的垂线n相交于点Q,可以把向量PQ看成是平面上的向量,其分别在b、c上的投影值分别为t和s(t和s为实数)。
因此,我们可以得到以下向量表示:PQ = tb+sc(2)将向量表示化为坐标表示,具体来说,我们可以将向量b、c和n 分别表示为坐标向量:b = (x1,y1,z1)c = (x2,y2,z2) n = (a1,a2,a3)则有:PQ = tb+sc = (x-x0,y-y0,z-z0)因此,我们可以得到以下解方程组的方法:(x-x0)/a1 = (y-y0)/a2 = (z-z0)/a3(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1)2. 从一般方程转化为向式方程若已知直线L的一般方程为:(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1)我们可以通过以下步骤将其转化为向式方程:(1)选取一点P(x0,y0,z0)在直线上,我们假设刚刚选取的点为P(x0,y0,z0)。



空间直线点法式空间直线是三维空间中的一条线段,由两个点所确定。
空间直线的参数方程可以用点和向量的形式表示,又称为向量方程。
空间直线还可以用点和点的形式表示,又称为点法式或一般方程。
为了方便描述,我们假设空间直线L平面上的一点为P0(x0,y0,z0),空间直线L的方向向量为a(x1,y1,z1)。
一、点向式空间直线L的点法式可以表示成如下形式:(x-x0)/x1 = (y-y0)/y1 = (z-z0)/z1这种表示方法的含义是,设L上的点Q(x,y,z),以P0点作为基准点,沿着方向向量a,假设走的距离为t(其中t为实数),则Q点的坐标可以用P0点的坐标和方向向量a的分量来表达,即:x=x0+tx1这样就得到了空间直线L的参数方程式。
二、一般式我们已经知道了点向式,现在来看一下空间直线的另一种表示方法——一般式。
其中,(A,B,C)为向量a的一个法向量。
这个式子怎么来的呢?我们可以将L上任一点P用向量形式表示,即P=P0+ta再将P带入空间直线L所在平面的解析式中,得到:(Ax1+By1+Cz1)-(Ax0+By0+Cz0)=0整理一下得到以上的一般式。
三、点向式和一般式的转换我们可以通过以下方式实现点向式和一般式的转换:1、从点向式转换为一般式:将点向式的分式形式变形,消去分母,即可得到一般式。
首先,把点向式中所有的“=”换为“-”,即得到以下形式:然后再将上述三个式子变形消去分母,得到一般式:(y1*z0-y0*z1)x+(x1*z0-x0*z1)y+(x0*y1-x1*y0)z+(x0*y1-x1*y0) = 02、从一般式转换为点向式:选取方向向量,利用向量的模长求分量,得到点向式。
首先,选取一个方向向量a(x1,y1,z1),其中至少有一个分量不为零。
我们可以假设x1=1,则有:因为x1=1,所以y1和z1都不为零。
我们可以求出y1和z1的模长,然后再利用上式求出y和z的分量,即可得到点向式。

直线点向式方程公式
点向式方程是几何学中表示直线方程的一种形式,其一般形式为:(X-X0)/A = (Y-Y0)/B = (Z-Z0)/C。
其中,(X0,Y0,Z0)是直线上的一个已知点,A、B、C为直线的方向向量。
这个方程的特点是可以直接看出直线的方向以及直线上的一个点的坐标。
对于二维平面中的情况,点向式方程可以简化为:(x-x0)/a=(y-y0)/b,其中(a,b)为直线的方向向量,(x0,y0)为直线上的一个已知点。
当直线水平时,方向向量的纵坐标b为0,此时方程变为x=x0;当直线垂直时,方向向量的横坐标a为0,此时方程变为y=y0。
点向式方程常用于求解几何问题,如求两条直线的交点、判断一个点是否在直线上等。
同时,点向式方程也有许多变形,如参数式、斜截距式等,这些都能更方便地解决某些具体问题。
参考:百度文库
在三维空间中,点向式方程可以以更为一般的形式出现,既适用于直线,也可用于表示平面。
在表示平面时,可以将其理解为一个特定点(x0,y0,z0)与平面上任意一点(x,y,z)的向量与法向量之间的点积为零。
对此问题进行进一步研究,我们会发现点向式方程的广泛应用,如物体在三维空间中的旋转动作、光线穿过某一点的反射与折射等。
它其实是一种通用的数学描绘方式,不仅在初高中数学课本中广泛运用,在高等数学、线性代数等课程中也有重要应用。
借助它能够更全面、深入地理解直线与空间的关系,揭示了几何与数学的内在联系。

直线方程化为点向式
数学中,形式化解决问题的方法可以有效地简化问题,并且帮助我们更好地理解和解决数学问题。
在这个文章中,我们将详细讨论如何将直线方程化为点向式。
一、直线方程的定义
在二维坐标系里,直线方程为y = mx + b,其中,m表示斜率,b表示y轴截距。
在三维空间中,直线方程为l = p + tv,其中,p表示线上任一点,v表示线的方向向量,t表示任意实数。
二、点向式的定义
点向式也称为向量式,表示形式为l = a + tb,其中,a表示线上任一点,b表示线的方向向量,t表示任意实数。
三、如何将直线方程化为点向式
我们来看一下如何将二维坐标系中的直线方程化为点向式:
首先,我们需要计算出直线的斜率,例如y = 2x + 3,它的斜率为2。
然后,我们需要选择直线上一个点,例如(0,3)。
接着,我们需要将斜率和选定的点代入到点向式中,得到l = (0,3) + t(1,2)。
至此,直线方程就被化为了点向式。
在三维空间中,将直线方程化为点向式也是类似的:
首先,我们需要选择任一点,例如(1,2,3)。
然后,我们需要计算出线的方向向量。
例如,一条垂直于x轴的直线的方向向量为(0,1,0)。
接着,我们将点和方向向量代入到点向式中,得到l = (1,2,3) + t(0,1,0)。
四、总结
总之,点向式的定义和使用对于解决一些数学问题非常有帮助。
化直线方程为点向式是一个很好的例子,可以更好地理解和解决数学问题。
在我们的日常生活中,点向式和直线方程两者的联系也十分紧密,需要我们认真学习和理解。
三维直线拟合公式
在三维空间中,拟合一条直线的公式可以根据不同的表示方法而变化。
以下给出两种常用的方法:
一、直线方程的三种表示方法
1.一般式:它实际上表示,直线是两个平面的交线,因此可以由两个平面方程得到,
即:
Ax + By + Cz + D = 0
2.点向式(标准方程):(m, n, p) 为直线方程的方向向量;(x0, y0, z0) 为直线上的一
个点。
m(x - x0) + n(y - y0) + p(z - z0) = 0
3.参数方程:由此就可以得到:
x = x0 + mt
y = y0 + nt
z = z0 + pt
其中(x0, y0, z0) 为直线上的一点,t 为参数。
二、利用最小二乘法拟合直线方程。
该方法的核心是利用离散点(实际点)与拟合
直线上的点(理想点)残差的平方和作为目标函数,求偏导计算最小值即可。
通过解多个点的矛盾方程,构建直线拟合经验公式:
y = a * x + b
在三维空间中,假设我们有一组三维点数据,其中每一个X均有一个Y与之对应,我们不妨构建矩阵,解矛盾方程求解即可。
黄岛区职业教育中心
2013---2014学年度第一学期电子教案
学科:数学
授课人:刘桂美
使用班级: 12财1、12财2、12财3
2013年9月 2 日
2013年9 月2 日备
概念:与一条直线平行的非零向量叫做这条直线的
v 表示。
:一条直线的方向向量不是唯一的。
v =(1,2)是一条直线的方向向量,v '=(2,)也是这条直线的一个方向向量。
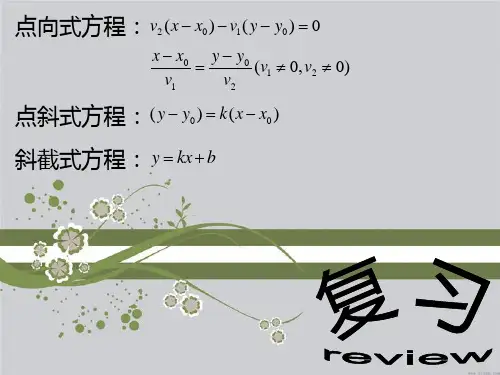
二、点向式方程
如图已知点000(,)
P x y v =(12,v v ),0,)y 并且一个方向向量为v =(12,v v )的方程。
是直线上任意一点,则0p p v ,又
00()p p x y y =--
)0= 0,以上方程又可以写成 ,直线与x 轴垂直
教师引导学生举例说明,
习
教师提出问题由学生讨论:线
教师引导学生整理推导点向式方程
学生记忆公式
v=(-1,
v的直线方
v=(0,2
v=(3,0
页习题1、。