2020届黑龙江省大庆实验中学高三下学期开学考试数学(理)试题

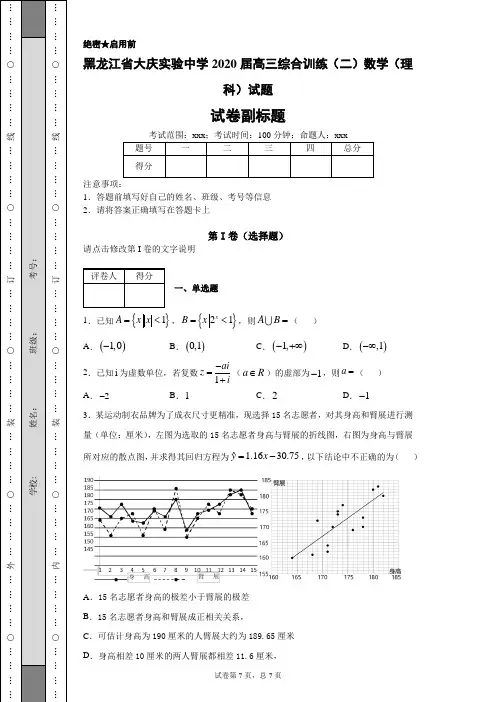
……外…………○……学校:___……内…………○……绝密★启用前 黑龙江省大庆实验中学2020届高三综合训练（二）数学（理科）试题 试卷副标题 注意事项： 1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上 第I 卷（选择题） 请点击修改第I 卷的文字说明 一、单选题 1．已知{}1A x x =<，{}21x B x =<，则A B =（ ） A ．()1,0- B ．()0,1 C ．()1,-+∞ D ．(),1-∞ 2．已知i 为虚数单位，若复数1ai z i -=+（a R ∈）的虚部为1-，则a =（ ） A ．2- B ．1 C ．2 D ．1- 3．某运动制衣品牌为了成衣尺寸更精准，现选择15名志愿者，对其身高和臂展进行测量（单位：厘米），左图为选取的15名志愿者身高与臂展的折线图，右图为身高与臂展所对应的散点图，并求得其回归方程为 1.160.5ˆ37y x =-，以下结论中不正确的为（ ）A ．15名志愿者身高的极差小于臂展的极差B ．15名志愿者身高和臂展成正相关关系，C ．可估计身高为190厘米的人臂展大约为189.65厘米……○…………订…………○…………线…………※※装※※订※※线※※内※※答※※题※※ ……○…………订…………○…………线…………4．函数()32ln x x f x x -=的图象大致为（ ） A ． B ． C ． D ．5．某几何体的三视图如图所示，则该几何体的体积为（ ）A ．16163π- B ．32163π-C ．1683π- D ．3283π-6．《九章算术》第三章“衰分”介绍比例分配问题，“衰分”是按比例递减分配的意思，通常称递减的比例为“衰分比”.如：已知A ，B ，C 三人分配奖金的衰分比为20%，若A 分得奖金1000元，则B ，C 所分得奖金分别为800元和640元.某科研所四位技术人员甲、乙、丙、丁攻关成功，共获得单位奖励68780元，若甲、乙、丙、丁按照一定的“衰分比”分配奖金，且甲与丙共获得奖金36200元，则“衰分比”与丁所获得的奖金分别为( )A ．20%，14580元B ．10%，14580元C ．20%，10800元D ．10%，10800元7．若0m >，0n >，且直线()()1120m x n y +++-=与圆222210x y x y +--+=相切，则m n +的取值范围是（ ）…………○…………装…………○……学校:___________姓名：___________班级：_…………○…………装…………○……8．我国古代数学家秦九韶左《数书九章》中记述了了“一斜求积术”，用现代式子表示即为：在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，则ABC 的面积S =()cos 3cos 0c B b a C ++=，且222 4c a b --=，则ABC 的面积为（ ） A B ．C D ．9．2018年9月24日，阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想，这一事件引起了数学界的震动，在1859年，德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题，也就是著名的黎曼猜想.在此之前，著名数学家欧拉也曾研究过这个问题，并得到小于数字x 的素数个数大约可以表示为n (x )≈x ln x 的结论（素数即质数，lg e ≈0.43429）.根据欧拉得出的结论，如下流程图中若输入n 的值为100，则输出k 的值应属于区间（ ） A ．(15,20] B ．(20,25] C ．(25,30] D ．(30,35] 10．已知双曲线C ：22221(0,0)x y a b a b -=>>的左、右焦点分别为()1,0F c -、()2,0F c ，且双曲线C 与圆222x y c +=在第一象限相交于点A ，且12AF AF =，则双曲线CA 1B 1CD 11．已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<，8f π⎛⎫= ⎪⎝⎭02f ⎛⎫= ⎪⎝⎭π且在()0,π上是单调函数，则下列说法正确的是（ ） A ．12ω= B ．82f π⎛⎫-= ⎪⎝⎭ C ．函数()f x 在,2ππ⎡⎤--⎢⎥⎣⎦上单调递减 D ．函数()f x 的图像关于点5,04π⎛⎫ ⎪⎝⎭对称12．定义在R 上的偶函数()f x 满足()()53f x f x -=+，且()224,012ln ,14x x x f x x x x ⎧-+≤<=⎨-≤≤⎩，若关于x 的不等式()()()210f x a f x a +++<在[]20,20-上有且仅有15个整数解，则实数a 的取值范围是（ ）A ．(]1,ln 22--B ．[)2ln33,2ln 22--C ．(]2ln33,2ln 22--D ．[)22ln 2,32ln3--第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题13．若65(x +的展开式的常数项是__________．14．已知向量(1,2)a =，(,1)b k =，且2a b +与向量a 的夹角为90°，则向量a 在向量b 方向上的投影为________.15．已知P ，E ，F 都在球面C 上，且P 在EFG ∆所在平面外，PE EF ⊥，PE EG ⊥，224PE GF EG ===，120EGF ︒∠=，在球C 内任取一点，则该点落在三棱锥P ﹣EFG 内的概率为_____．三、双空题…………装…………○校:___________姓名：___________班…………装…………○16．已知数列{}n a 的各项都是正数，()2*11n n n a a a n N ++-=∈.若数列{}n a 各项单调递增，则首项1a 的取值范围是________；当123a =时，记1(1)1n n n b a --=-，若1220191k b b b k <+++<+，则整数k =________. 四、解答题 17．若ABC 的内角A ，B ，C 的对边为a ，b ，c ，且224()si sin n sin sin sin 3A B C B C -=-. （1）求cos A ； （2）若ABC A 的角平分线AD 长的最大值. 18．如图，四棱锥S ﹣ABCD 中，SD ＝CD ＝SC ＝2AB ＝2BC ，平面ABCD ⊥底面SDC ，AB ∥CD ，∠ABC ＝90°，E 是SD 中点． （1）证明：直线AE //平面SBC ； （2）点F 为线段AS 的中点，求二面角F ﹣CD ﹣S 的大小． 19．2019年春节期间，我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况，在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数，统计发现这一时间段内共有600辆车通过该收费点，它们通过该收费点的时刻的频率分布直方图如下图所示，其中时间段9:20~9:40记作区间[)20,40，9:40~10:00记作[)40,60，10:00~10:20记作[)60,80，10:20~10:40记作[)80,100.例如：10点04分，记作时刻64.…线…………○………线…………○……（1）估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值（同一组中的数据用该组区间的中点值代表）；（2）为了对数据进行分析，现采用分层抽样的方法从这600辆车中抽取10辆，再从这10辆车中随机抽取4辆，设抽到的4辆车中，在9:20~10:00之间通过的车辆数为X，求X的分布列与数学期望；（3）由大数据分析可知，车辆在每天通过该收费点的时刻T服从正态分布()2,Nμσ，其中μ可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替，2σ可用样本的方差近似代替（同一组中的数据用该组区间的中点值代表），已知大年初五全天共有1000辆车通过该收费点，估计在9:46~10:40之间通过的车辆数（结果保留到整数）.参考数据：若()2,T Nμσ~，则()0.6827P Tμσμσ-<≤+=，()220.9545P Tμσμσ-<≤+=，()330.9973P Tμσμσ-<≤+=.20．已知椭圆:C22221(0)x ya ba b+=>>，焦距为2c，直线bx y-+=过椭圆的C左焦点.（1）求椭圆C的标准方程；（2）若直线20bx y c-+=与y轴交于点,,P A B是椭圆C上的两个动点,APB∠的平分线在y轴上,PA PB≠.试判断直线AB是否过定点，若过定点，求出定点坐标;若不过定点，请说明理由.21．已知函数()lnf x x ax b=--.（1）求函数()f x的极值；（2）若不等式()f x ex≤-恒成立，求b的最小值（其中e为自然对数的底数）.22．在平面直角坐标系xOy 中，以坐标原点O 为极点，以x 轴正半轴为极轴，建立极坐标系，曲线C 的极坐标方程为2212,1sin ρθ=+射线(0)4πθρ=≥交曲线C 于点A ,倾斜角为α的直线l 过线段OA 的中点B 且与曲线C 交于P 、Q 两点. (1)求曲线C 的直角坐标方程及直线l 的参数方程; (2)当直线l 倾斜角α为何值时, |BP |·|BQ |取最小值, 并求出|BP |·|BQ |最小值. 23．选修4-5：不等式选讲已知函数() 1.f x x =+ （Ⅰ）解不等式()32f x x >-+； （Ⅱ）已知0,0a b >>，且2a b +=()f x x -≤参考答案1．D【解析】【分析】分别解出集合,A B 、然后求并集.【详解】 解：{}{}111A x x x x =<=-<<，{}{}210x B x x x =<=< A B =(),1-∞故选：D【点睛】考查集合的并集运算，基础题.2．C【解析】分析：先化简复数z,再根据复数z 的虚部为-1求a 的值. 详解：由题得1ai z i-=+=(1),1, 2.1(1)(1)22ai ai i a ai a a i i i ----==∴-=-∴=++- 故答案为C点睛：（1）本题主要考查复数的除法和复数的实部与虚部，意在考查学生对这些基础知识的掌握能力.(2)复数(,)z a bi a b R =+∈的实部是a,虚部是b ，不是bi.3．D【解析】【分析】根据散点图和回归方程的表达式，得到两个变量的关系，A 根据散点图可求得两个量的极差，进而得到结果；B ，根据回归方程可判断正相关；C 将190代入回归方程可得到的是估计值，不是准确值，故不正确；D ，根据回归方程x 的系数可得到增量为11.6厘米，但是回归方程上的点并不都是准确的样本点，故不正确.【详解】A ，身高极差大约为25，臂展极差大于等于30，故正确；B ，很明显根据散点图像以及回归直线得到，身高矮臂展就会短一些，身高高一些，臂展就长一些，故正确；C ，身高为190厘米，代入回归方程可得到臂展估计值等于189.65厘米，但是不是准确值，故正确；D ，身高相差10厘米的两人臂展的估计值相差11.6厘米，但并不是准确值，回归方程上的点并不都是准确的样本点,故说法不正确.故答案为D.【点睛】本题考查回归分析，考查线性回归直线过样本中心点，在一组具有相关关系的变量的数据间，这样的直线可以画出许多条，而其中的一条能最好地反映x 与Y 之间的关系，这条直线过样本中心点．线性回归方程适用于具有相关关系的两个变量，对于具有确定关系的两个变量是不适用的, 线性回归方程得到的预测值是预测变量的估计值，不是准确值.4．A【解析】【分析】先求出函数的定义域，再判断奇偶性，然后由函数图像的变化趋势可得答案【详解】 解：函数的定义域为{}0x x ≠， 因为3322()ln ln ()()()x xx x f x f x x x -----===-，所以()f x 为偶函数，所以排除C,D,又因为当0x >时，322ln ln ()x x x f x x x x-==-， 当x →+∞时，()f x →+∞，所以排除B故选：A【点睛】此题考查了由函数关系式识别函数图像，利用了函数的奇偶性和函数值的变化趋势进行了辨别，属于基础题.5．D【解析】【分析】由三视图可知：该几何体为一个半圆柱挖取一个倒立的四棱锥． 【详解】解：由三视图可知：该几何体为一个半圆柱挖取一个倒立的四棱锥． ∴该几何体的体积2211244223V π=⨯⨯⨯-⨯⨯ 3283π=-. 故选D ． 【点睛】本题考查了三棱台的三视图的有关知识、圆柱与四棱锥的体积计算公式，考查了推理能力与计算能力，属于中档题． 6．B 【解析】 【分析】设“衰分比”为q ，甲获得的奖金为1a ，联立方程解得10.1,20000q a ==，得到答案. 【详解】设“衰分比”为q ，甲获得的奖金为1a ，则()()()23111111168780a a q a q a q +-+-+-=.()211136200a a q +-=，解得10.1,20000q a ==，故()31114580a q -=.故选：B . 【点睛】本题考查了等比数列的应用，意在考查学生的计算能力和应用能力. 7．B 【解析】 【分析】首先由圆的标准方程求出圆心坐标和半径r ，利用直线与圆相切时，圆心到直线的距离等于圆的半径以及点到直线的距离公式列出关系式，整理后利用基本不等式变形，再设m n x +=，得到关于x 的不等式，解不等式即可. 【详解】由圆222210x y x y +--+=，得()()22111x y -+-=，得到圆心坐标为()1,1，半径1r =，∵直线()()1120m x n y +++-=与圆相切， ∴圆心到直线的距离1d ==，整理得：212m n m n mn +⎛⎫++=≤ ⎪⎝⎭，设()0m n x x +=>，则有214x x +≤，即2440x x --≥，解得：2x ≥+，则m n +的取值范围为)2⎡++∞⎣. 故选：B 【点睛】本题考查了直线与圆的位置关系，同时考查了点到直线的距离公式，基本不等式，以及一元二次不等式的解法，是中档题. 8．B 【解析】 【分析】由已知结合正弦定理及和差角公式进行化简，求得cos C ，再结合已知及余弦定理，求得ab 的值，代入已知公式，即可求解. 【详解】由题意，因为()cos 3cos 0c B b a C ++=，所以()sin cos sin 3sin cos 0C B B A C ++=， 即sin()3sin cos 0B C A C ++=，又由sin()sin B C A +=，所以sin 3sin cos 0A A C +=，由因为(0,)A π∈，所以sin 0A >，所以13cos 0C +=，即1cos 3=-C ， 因为2224c a b --=，由余弦定理可得22241cos 223a b c C ab ab +--===-，解得6ab =，则ABC 的面积为S ===故选：B. 【点睛】本题主要考查了正弦定理、余弦定理和两角和与差的正弦函数公式的化简求值的综合应用，意在考查推理与运算能力，属于中档试题. 9．B 【解析】 【分析】由流程图可知其作用为统计100以内素数的个数，将x =100代入n (x )≈x ln x可求得近似值，从而得到结果. 【详解】该流程图是统计100以内素数的个数由题可知小于数字x 的素数个数大约可以表示为n (x )≈x ln x则100以内的素数个数为n (100)≈100ln 100=1002ln 10=50lg10lge=50lge ≈22本题正确选项：B 【点睛】本题考查判断新定义运算的问题，关键是能够明确流程图的具体作用. 10．A 【解析】 【分析】运用双曲线的定义和条件，求得1AF ，2AF ，由直径所对的圆周角为直角，运用勾股定理和离心率公式，计算可得所求值． 【详解】双曲线C 与圆222x y c +=在第一象限相交于点A ， 可得122AF AF a -=，由12AF AF =，可得(13AF a =+，(21AF a =，由12AF AF ⊥，可得2221212||||AF AF F F +=，即为((2221244a a c +++=，即有2221644c e a +===+即有1e =． 故选A ． 【点睛】本题考查双曲线的离心率的求法，注意运用直径所对的圆周角为直角，以及双曲线的定义，考查化简运算能力，属于中档题． 11．B 【解析】 【分析】根据函数()f x ，在()0,π上是单调函数，确定 01ω<≤，然后一一验证， A.若12ω=，则()12sin 2ϕ⎛⎫=+ ⎪⎝⎭f x x ，由02f π⎛⎫= ⎪⎝⎭，得34πϕ=，但13sin 84822πππ⎛⎫⨯+≠ ⎛⎫= ⎪⎭⎪⎝⎭⎝f .B.由8f π⎛⎫= ⎪⎝⎭02f π⎛⎫= ⎪⎝⎭，确定()222sin 33π⎛⎫=+⎪⎝⎭f x x ，再求解8f π⎛⎫- ⎪⎝⎭验证.C.利用整体法根据正弦函数的单调性判断.D.计算54f π⎛⎫⎪⎝⎭是否为0. 【详解】因为函数()f x ，在()0,π上是单调函数， 所以2T ≥π ，即22ππω≥，所以 01ω<≤ ，若12ω=，则()12sin 2ϕ⎛⎫=+ ⎪⎝⎭f x x ，又因为02f π⎛⎫= ⎪⎝⎭，即1sin 0222ππϕ⎛⎫⎛⎫⨯+= ⎪⎝=⎪⎝⎭⎭f ，解得34πϕ=， 而13sin 84822πππ⎛⎫⨯+≠ ⎛⎫= ⎪⎭⎪⎝⎭⎝f ，故A 错误. 由2sin 022πωπϕ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭f ，不妨令2ωπϕπ+= ，得2πωϕπ=-由sin 882ππωϕ⎛⎫⎛⎫=⨯+=⎪ ⎪⎝⎭⎝⎭f ，得 2+84ππωϕπ⨯+=k 或32+84ππωϕπ⨯+=k 当2+84ππωϕπ⨯+=k 时，2=23k πω+，不合题意. 当32+84ππωϕπ⨯+=k 时，22=33k πω+，此时()222sin 33π⎛⎫=+⎪⎝⎭f x x所以222272sin 2sin 2sin 8383383122ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=⨯-+=⨯-+== ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭f ，故B 正确.因为22,,0,2333ππππ⎡⎤⎡⎤∈--+∈⎢⎥⎢⎥⎣⎦⎣⎦x x ，函数()f x ，在0,3π⎛⎫ ⎪⎝⎭上是单调递增，故C 错误. 525232sin 2sin 043432f ππππ⎛⎫⎛⎫=⨯+==≠ ⎪ ⎪⎝⎭⎝⎭，故D 错误. 故选：B 【点睛】本题主要考查三角函数的性质及其应用，还考查了运算求解的能力，属于较难的题. 12．B 【解析】 【分析】由()()53f x f x -=+得函数图象关于直线4x =对称，又函数为偶函数，得函数是周期函数，且周期为8，区间[20,20]-含有5个周期，因此题中不等式在一个周期内有3个整数解，通过研究函数()f x 在[0,4]的性质，结合图象可得结论． 【详解】∵()()53f x f x -=+，∴函数图象关于直线4x =对称，又函数为偶函数，∴函数是周期函数，且周期为8，区间[20,20]-含有5个周期，关于x 的不等式()()()210f x a f x a +++<在[4,4]-上有3个整数解． [0,1)x ∈时，2()24f x x x =-+是增函数， [1,4]x ∈时，()2ln f x x x =-，2()1f x x'=-，12x ≤<时，()0f x '<，()f x 递减，24x <≤时，()0f x '>，()f x 递增，2x =时，()f x 取得极小值(2)22ln 2f =-，(1)1f =，(3)32ln 31f =-<，利用偶函数性质，作出()f x 在[4,4]-上的图象，如图． 由()()()210fx a f x a +++<得[()1][()]0f x f x a ++<，若0a -≤，则原不等式无解，故0a ->，1()f x a -<<-，要使得不等式1()f x a -<<-在[4,4]-上有3个整数解， 则22ln 232ln3a -<-≤-，即2ln332ln 22a -≤<-． 故选：B ．【点睛】本题考查不等式的整数解问题，考查了函数的奇偶性、对称性、周期性，用导数研究函数的单调性、极值等，考查的知识点较多，对学生的分析问题解决问题的能力、转化与化归能力要求较高，属于难题． 13．5 【解析】二项式56x⎛ ⎝展开式的通项公式：1530652155r r r r rr T C x C x --+==（）令153002r -=，解得4r =． ∴常数项455C == 即答案为514【解析】 【分析】由题可知()20a b a +⋅=,依据数量积的坐标公式可求出k ,即求出向量b ,从而得到向量a 在向量b 方向上的投影为cos ,a b a a b b⋅⋅<>=.【详解】因为向量(1,2)a =,(,1)b k =, 则2(2,5)a b k +=+,又2a b +与向量a 的夹角为90°, 所以()20a b a +⋅=,即2100k ++=, 解得12k =-,即(12,1)b =-,因此向量a 在向量b 方向上的投影为cos ,145a b a a b b⋅⋅<>===,故答案为. 【点睛】本题综合考查了数量积的坐标运算及投影的求法,难度不大.15．32π【解析】 【分析】由题意画出图形，求出三棱锥外接球的半径，再分别求出三棱锥及其外接球的体积，由测度比为体积比得答案． 【详解】 如图，在EGF ∆中，由已知可得2EG GF ==，120EGF ︒∠=，可得EF =EFG ∆的外接圆的半径为r 2r =，可得2r，再设EGF ∆的外心为1G ，过1G 作底面EGF 的垂线1G O ，且使1122G O PE ==，连接OE ，则OE =OE 为三棱锥P EFG -的外接球的半径，则3433V π=⨯=球；11221204323P EGF V sin ︒-=⨯⨯⨯⨯⨯=， 由测度比为体积比，可得在球C 内任取一点，则该点落在三棱锥P ﹣EFG 内的概率为3=．． 【点精】本题考查球内接多面体及其体积、考查几何概型等基础知识，考查运算求解能力，属于中档题．16．(0,2) 4- 【解析】 【分析】本题根据正数数列{}n a 是单调递增数列，可列出211120n n n n a a a a +++-=-<，通过求出1n a +的取值范围，得到2a 的取值范围，逆推出1a 的取值范围；第二空主要是采用裂项相消法求出122019b b b ++⋯+的表达式，然后进行不等式范围计算，即可得到结果．【详解】由题意，正数数列{}n a 是单调递增数列，且211n n n a a a ++-=，∴211120n n n n a a a a +++-=-<，解得1(0,2)n a +∈，2(0,2)a ∴∈．∴21221[,2)4a a a =-∈-．10a >，102a ∴<<．又由211n n n aa a ++-=，可得：2111111111n n n n n a a a a a ++++==---． ∴111111n n n a a a ++=+-．1(1)1n n n b a --=-，∴122019123201911111111b b b a a a a ++⋯+=-+-⋯+---- 112232017201820182019111111111()()()()1a a a a a a a a a =-+++-⋯-+++- 1122320172018201820191111111111a a a a a a a a a =--++-⋯--++- 1120191111a a a =-+- 2019912a =-+．123a =，且数列{}na 是递增数列， 20192(,2)3a ∴∈，即2019113(,)22a ∈， 201991432a ∴-<-+<-．∴整数4k =-．故答案为：(0,2)；-4． 【点睛】本题考查了数列递推关系、裂项相消法的应用和数列的周期性，考查了推理能力与不等式的计算能力，属于较难的中档题．17．（1）13；（2）3【解析】 【分析】（1）由正弦定理将已知式化角为边，再由余弦定理求出cos A ； （2）由（1）的结论1cos 3A =及ABCsin A =和4bc =.再由二倍角公式求出cos23A =.将ABC 拆分成两个三角形ABD △和ACD ，利用面积相等，求出AD ，再利用基本不等式求出其最大值. 【详解】解：（1）由正弦定理sin sin sin A B Ca b c==， 及224()si sin n sin sin sin 3A B C B C -=-， 可得224()3b c a bc -=-，即22223b c a bc +-=， ∴由余弦定理得：2221cos 23b c a A bc +-==；（2）由1cos 3A =，得sin A ，cos2A ==，1sin 2S ABC bc A ==，则4bc =， 由ABCABDACDS SS=+得111sin sin sin 22222A A AB AC A AB AD AC AD ⋅⋅=⋅⋅+⋅⋅，2cos2cos 22A Abc bc A AD b c ∴=≤==+， 当且仅当2b c ==时，等号成立，即maxAD=.【点睛】本题考查了正弦定理、余弦定理的应用，二倍角公式，基本不等式的应用，属于中档题. 18．（1）详见解析；（2）30°．【解析】【分析】（1）取SC中点G，连接BG，EG，推导出四边形AEGB为平行四边形，从而AE∥BG，进而AE∥平面SBC；（2）取CD中点O，连接OS，OA ，推导出四边形ABCD为矩形，AO⊥CO，AO⊥CD，以O为原点，OS所在直线为x轴，OC所在直线为y轴，OA所在直线为z轴，建立空间直角坐标系，利用向量法能求出二面角F﹣CD﹣S的大小．【详解】（1）证：如图，取SC中点G，连接BG，EG，∵EG为△SDC的中位线，∴EG∥CD，且EG12CD =，∵AB∥CD，且AB12CD=，∴EG∥CD，且EG＝AB，∴四边形AEGB为平行四边形，∴AE∥BG，∵BG⊂平面SBC，AE⊄平面SBC，∴AE∥平面SBC；（2）解：设AB＝1，则BC＝1，CD＝2，取CD中点O，连接OS，OA ，∴CO12CD AB ==，∵AB∥CD，∠ABC＝90°，∴四边形ABCO为矩形，∴AO⊥CO，AO⊥CD，平面ABCD ∩平面SDC ＝CD ，∴AO ⊥平面SDC ，AO ⊥SO ， ∵△SDC 为正三角形，∴SO ⊥CD ，以O 为原点，OS 所在直线为x 轴，OC 所在直线为y 轴，OA 所在直线为z 轴，建立如图所示的空间直角坐标系，A （0，0，1），S0，0），C （0，1，0），D （0，﹣1，0），F0，12），FC =（，1，12-），FD =（，﹣1，12-）， 设平面FCD 的一个法向量m =（a ，b ，c ），则3102231022FC m x y z FD m x y z ⎧⋅=-+-=⎪⎪⎨⎪⋅=---=⎪⎩，取x ＝1，得m =（1，0，，由题意取平面SDC 的一个法向量n OA ==（0，0，1）， 设二面角F ﹣CD ﹣S 的大小为θ，则3cos 2m n m nθ-⋅===， 由图可知，θ为锐角，∴θ＝30°， ∴二面角F ﹣CD ﹣S 的大小为30°． 【点睛】本题主要考查线面平行的证明，考查二面角的求法，考查运算求解能力，属于中档题． 19．（1）10点04分（2）分布列见解析，()85E X =（3）819辆【解析】 【分析】（1）利用频率分布直方图和平均数的计算公式，即可求得这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值；（2）结合频率分布直方图和分层抽样的方法求得随机变量X 的可能取值0,1,2,3,4，求出相应的概率，得到X 的分布列，利用期望的公式，求得其数学期望；（3）由（1）可得64,18μσ==，得到()2,T N μσ~，得到概率，即可求解在9:46~10:40这一时间段内通过的车辆数. 【详解】（1）由题意，这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为()300.005500.015700.020900.0102064⨯+⨯+⨯+⨯⨯=，即10点04分.（2）结合频率分布直方图和分层抽样的方法可知：抽取的10辆车中，在10:00前通过的车辆数就是位于时间分组中在[)2060,这一区间内的车辆数，即()0.0050.01520104-⨯⨯=，所以X 的可能取值为0，1，2，3，1.所以()46410C 10C 14P X ===，()3161410C C 81C 21P X ===，()2264410C C 32C 7P X ===， ()1364410C C 43C 35P X ===，()0464410C C 14C 210P X ===，所以X 的分布列为所以()1834180123414217352105E X =⨯+⨯+⨯+⨯+⨯=. （3）由（1）可得64μ=，()()()()2222230640.150640.370640.490640.2324σ=-⨯+-⨯+-⨯+-⨯=，所以18σ=.估计在9:46~10:40这一时间段内通过的车辆数，也就是46100T <≤通过的车辆数， 由()2,T N μσ~，()()()226418642180.818622P T P T P T μσμσμσμσ-<≤+-<≤+-<≤+⨯=+=，所以，估计在9:46~10:40这一时间段内通过的车辆数为10000.8186819⨯≈辆. 【点睛】本题主要考查了离散型随机变量的分布列和数学期望的求解，以及正态分布及频率分布直方图的应用，其中解答中认真审题，正确求解相应的概率，得到其分布列，利用公式准确运算时解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题.20．(1)22184x y +=;(2)过定点(0,1)【解析】 【分析】(1)因为直线0bx y -+=过椭圆的左焦点,故令0y ＝,得x c ==-,又因为离心率为2,从而求出2b ＝,又因为222a b c =+,求出a 的值,从而求出椭圆C 的标准方程; (2)先求出点P 的坐标,设直线AB 的方程为y kx m +＝,联立方程组,利用根与系数的关系,设()11,A x y ,()22,B x y ,得到1228(1)4k m k k m -+=-,又因为APB ∠的平分线在y 轴上,所以120k k +=,从而求出m 的值,得到直线AB 的方程为1y kx ＝+过定点坐标.【详解】解:(1)因为直线0bx y -+=过椭圆的左焦点,故令0y ＝,得x c b=-=-，2c a b ∴==,解得2b ＝.又2222212a b c b a =+=+,解得a =∴椭圆C 的标准方程为:22184x y +=.(2)由(1)得2c ==,∴直线20bx y c -+=的方程为240x y -+= 令0x ＝得,4y ＝,即(0,4)P .设直线AB 的方程为y kx m =+ 联立方程组22184y kx m x y =+⎧⎪⎨+=⎪⎩,消去y 得,()222214280k x kmx m +++-=设()11,A x y ,()22,B x y ,∴122421km x x k +=-+,21222821m x x k -=+ 则直线PA 、PB 的斜率111144y m k k x x --==+, 222244y m k k x x --==+ 所以()12122212(4)(4)(4)8(1)22284m x x m km k m k k k k x x m m -+---+=+=+=-- APB ∠的平分线在y 轴上,120k k ∴+=,即28(1)04k m m -=-又PA PB ≠,0k ∴≠,1m ∴＝.即直线AB 的方程为1y kx ＝+,过定点(0,1). 【点睛】本题考查了椭圆的方程,考查了直线与椭圆的位置关系.求椭圆方程时,经常会用到222c a b =-,这里易错点就是和双曲线的222c a b =+ 进行混淆.求解直线和圆锥曲线问题时,一般要设出直线方程,与圆锥曲线方程进行联立,消元后韦达定理得到交点坐标的关系,再根据具体的题目往下做.21．（1）当0a ≤时，()f x 无极值；当0a >时，()f x 极大值为ln 1a b ---，无极小值 （2）-1 【解析】 【分析】（1）求出导函数()f x '，确定函数单调性，得极值，需分类讨论．（2）()0f x ex +≤恒成立，设()()h x f x ex =+，求出()h x 的最大值max ()h x ，由max ()0h x ≤得出,a b 满足的不等关系1ln()b a e ≥---，然后得1ln()()b a e a e a e a e +-≥->--，求得1ln()()()x e F x x e x e+-=->-的最小值即得结论． 【详解】 （1）解()11(0)axf x a x x x-'=-=>， 当0a ≤时，()0f x '>恒成立，函数()f x 在()0,∞+上单调递增，无极值. 当0a >时，由()0f x '>，得10x a <<，函数()f x 在10,a ⎛⎫⎪⎝⎭上单调递增，由()0f x '<，得1x a>， 函数()f x 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减，()f x 极大值为11ln 1ln 1f b a b a a ⎛⎫=--=--- ⎪⎝⎭，无极小值.综上所述，当0a ≤时，()f x 无极值；当0a >时，()f x 极大值为ln 1a b ---，无极小值. （2）由()f x ex ≤-可得()ln f x x ax b ex =--≤-， 设()ln ()h x x e a x b =+--，所以1()h x e a x'=+-，0x >， 当a e ≤时，()0h x '>，()h x 在()0,∞+上是增函数，所以()0h x ≤不可能恒成立， 当a e >时，由1()0h x e a x '=+-=，得1x a e=-， 当10,x a e ⎛⎫∈ ⎪-⎝⎭时，()0h x '>，()h x 单调递增，当1,x a e ⎛⎫∈+∞⎪-⎝⎭时，()0h x '<，()h x 单调递减， 所以当1x a e =-时，()h x 取最大值，1ln()10h a e b a e ⎛⎫=----≤ ⎪-⎝⎭，所以ln()10a e b -++≥，即1ln()b a e ≥---，所以1ln()()b a e a e a e a e+-≥->--，令1ln()()()x e F x x e x e +-=->-，221()1ln()ln()()()()x e x e x e x e F x x e x e ------'=-=--， 当()1,x e ∈++∞时，()0F x '>，()F x 单调递增， 当(),1x e e ∈+时，()0F x '<，()F x 单调递减，所以当1x e =+时，()F x 取最小值，即()(1)1F x F e ≥+=-，所以ba e-的最小值为-1. 【点睛】本题考查用导数求函数的极值，用导数研究不等式恒成立问题．考查转化与化归思想．解题关键是把不等式恒成立转化为求函数的最值．本题对学生分析问题解决问题的能力、运算求解能力要求较高，属于难题．22．（1）曲线C 的直角坐标方程为221126x y +=；直线l 的参数方程为1cos 1sin x t y t αα=+⎧⎨=+⎩（t 为参数））（2）当2πα=时,BP BQ ⋅取得最小值为92【解析】 【分析】（1）由222sin x y y ρρθ⎧=+⎨=⎩求得曲线C 的直角坐标方程；先求出曲线C 与直线l 的交点A 的坐标,即可得到OA 的中点B ,进而求解即可；（2）由（1）,将直线l 的参数方程代入到曲线C 的直角坐标方程中,由参数的几何意义可得1222299cos 2sin 1sin BP BQ t t ααα⋅===++,进而求解即可. 【详解】（1）由题,因为22121sin ρθ=+,即()221sin 12ρθ+=, 因为222sin x y yρρθ⎧=+⎨=⎩, 所以22212x y y ++=,即22212x y +=,则曲线C 的直角坐标方程为221126x y +=,因为射线(0)4πθρ=≥交曲线C 于点A ,所以点A 的极坐标为4π⎛⎫ ⎪⎝⎭,则点A 的直角坐标为()2,2,所以OA 的中点B 为()1,1,所以倾斜角为α且过点B 的直线l 的参数方程为1cos 1sin x t y t αα=+⎧⎨=+⎩（t 为参数）.（2）将直线l 的参数方程1cos 1sin x t y t αα=+⎧⎨=+⎩（t 为参数）代入曲线C 的方程221126x y+=中,整理可得()()222cos2sin 2cos 4sin 90t t αααα+++-=,设P 、Q 对应的参数值分别是1t 、2t ,则有12229cos 2sin t t αα-=+,则1222299cos 2sin 1sin BP BQ t t ααα⋅===++, 因为(]0,απ∈,当sin 1α=,即2πα=时,BP BQ ⋅取得最小值为92【点睛】本题考查极坐标方程与直角坐标方程的转化,考查直线的参数方程,考查最值问题. 23．（Ⅰ）()(),30,-∞-+∞； （Ⅱ）见解析.【解析】 【分析】（Ⅰ）整理()32f x x >-+得：123x x +++>，由绝对值的几何意义即可解不等式。

2020年黑龙江省大庆实验中学高考数学综合训练试卷(理科)(四)一、选择题（本大题共12小题，共60.0分）1.已知i是虚数单位，则复数10i1−i=()A. −4+2iB. 4−2iC. −5−5iD. −5+5i2.已知集合A={0,1，2，3}，B={x|2x2−9x+9≤0}，则A∩B=()A. {0,1}B. {1,2}C. {2,3}D. {0,1，2}3.“x=1”是“x2−2x+1=0”的()A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件4.已知单位向量a⃗，b⃗ 满足：|a⃗+2b⃗ |=√3，则：|a⃗−2b⃗ |=()A. √2B. √5C. √3D. √75.已知tan(α+5π12)=2，则tan(α+π6)的值为()A. 13B. 1C. 2D. 36.函数f(x)=x2|e x−1|的图象大致是()A. B.C. D.7.中国铁路总公司相关负责人表示，到2018年底，全国铁路营业里程达到13.1万公里，其中高铁营业里程2.9万公里，超过世界高铁总里程的三分之二，如图是2014年到2018年铁路和高铁运营里程(单位：万公里)的折线图，以下结论不正确的是()A. 每相邻两年相比较，2014年到2015年铁路运营里程增加最显著B. 从2014年到2018年这5年，高铁运营里程与年价正相关C. 2018年高铁运营里程比2014年高铁运营里程增长80%以上D. 从2014年到2018年这5年，高铁运营里程数依次成等差数列8. 如图，正方体ABCD −A 1B 1C 1D 1中，M 是棱DD 1的中点，则过M 且与直线AB和B 1C 1都垂直的直线有( )A. 1条B. 2条C. 3条D. 无数条 9. 已知函数f (x )=sin(ωx +π6)(ω>0)在区间[−π4,2π3]上单调递增，则ω的取值范围为( ) A. (0,83]B. (0,12]C. [12,83]D. [38,2] 10. 如图，双曲线C ：x 2a 2−y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1(−c,0)，F 2(c,0)，A 为双曲线C 的右支上一点，且|AF 1|=2c ，AF 1与y 轴交于点B ，若F 2B 是∠AF 2F 1的平分线，则双曲线C 的离心率e =( )A. √5−1B. 1+√52C. 3+√52D. √5 11. 设a =log 1312，b =log 1323，c =log 343，则a,b,c 的大小关系为( ) A. a >b >cB. b >c >aC. c >a >bD. c >b >a 12. f(x)={ln |x | , x ≠00 , x =0，则方程[f(x)]2−f(x)=0的不相等实根个数为( ) A. 3 B. 5 C. 6 D. 4二、填空题（本大题共4小题，共20.0分）13. (√x 3−13√x 3)10的展开式中含x 2项的系数为______． 14. 已知公差不为零的等差数列{a n }中，a 1=1，且a 2，a 5，a 14成等比数列，{a n }的前n 项和为S n ，b n =(−1)n S n .则数列{b n }的前2n 项和T 2n =______．15. 已知直线y =x +a 与圆x 2+y 2=4交于A 、B 两点，且OA ⃗⃗⃗⃗⃗ ⋅OB⃗⃗⃗⃗⃗⃗ =0，其中O 为坐标原点，则正实数a 的值为______ ．16. 在△ABC 中，角A ，B ，C 所对的边为a ，b ，c ，已知2bcosA =2c −√3a ，则∠B =___ ．三、解答题（本大题共7小题，共82.0分）17. 若数列{a n }满足a 1=1，a n+1=3a n (n ∈N ∗).(1)求{a n }的通项公式；(2)等差数列{b n }的各项均为正数，其前n 项和为T n ，且T 3=15，又a 1+b 1，a 2+b 2，a 3+b 3成等比数列，求T n ．18. 已知四棱锥P −ABCD 的三视图如图所示，E 是侧棱PC 上的动点．(1)求证：BD ⊥AE;(2)若点E为PC的中点，求二面角D−AE−B的大小．19.某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温(单位：℃)有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20,25)，需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：以最高气温位于各区间的频率代替最高气温位于该区间的概率．(1)求六月份这种酸奶一天的需求量X(单位：瓶)的分布列；(2)设六月份一天销售这种酸奶的利润为Y(单位：元)，当六月份这种酸奶一天的进货量n(单位：瓶)为多少时，Y的数学期望达到最大值？20. 已知函数f(x)=ax +ln x +1．(1)讨论函数f(x)零点的个数；(2)对任意的x >0，f(x)⩽xe x 恒成立，求实数a 的取值范围．21. 已知椭圆C ：x 2a 2+y 2b 2=1(a >b >0)的左、右顶点分别为A ，B ，且长轴长为8，T 为椭圆上任意一点，直线TA ，TB 的斜率之积为−34．(1)求椭圆C 的方程；(2)设O 为坐标原点，过点M(0,2)的动直线与椭圆C 交于P ，Q 两点，求OP ⃗⃗⃗⃗⃗ ·OQ ⃗⃗⃗⃗⃗⃗ +MP ⃗⃗⃗⃗⃗⃗ ·MQ⃗⃗⃗⃗⃗⃗⃗ 的取值范围．22. 在直角坐标系xOy 中，曲线C 1的参数方程为{x =1+cosαy =sinα (α为参数).以坐标原点O 为极点，x轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ=1，直线l 的极坐标方程为θ=π4(ρ∈R)．(1)求：①曲线C1的普通方程；②曲线C2与直线l交点的直角坐标；)，点N是曲线C1上的点，求△MON面积的最大值．(2)设点M的极坐标为(6,π323.已知函数f(x)=|x|+|x−4|．(1)若f(x)≥|m+2|恒成立，求实数m的最大值；(2)记(1)中m的最大值为M，正实数a，b满足a2+b2=M，证明：a+b≥2ab．-------- 答案与解析 --------1.答案：D解析：解：10i1−i =10i(1+i)(1−i)(1+i)=−10+10i2=−5+5i．故选：D．直接利用复数代数形式的乘除运算化简得答案．本题考查复数代数形式的乘除运算，是基础题．2.答案：C解析：解：B={x|32≤x≤3}；∴A∩B={2,3}．故选：C．可求出集合B，然后进行交集的运算即可．考查列举法、描述法的定义，一元二次不等式的解法，以及交集的运算．3.答案：A解析：∵x2−2x+1=0有两个相等的根x=1，∴“x=1”是“x2−2x+1=0”的充要条件．4.答案：D解析：解：单位向量a⃗，b⃗ 满足：|a⃗+2b⃗ |=√3，可得(a⃗+2b⃗ )2=3，化为a⃗2+4a⃗⋅b⃗ +4b⃗ 2=3，即为1+4a⃗⋅b⃗ +4=3，可得a⃗⋅b⃗ =−12，则|a⃗−2b⃗ |=√(a⃗−2b⃗ )2=√a⃗2−4a⃗⋅b⃗ +4b⃗ 2=√1+4×12+4=√7．故选：D．。

大庆实验中学实验一部2020届高三仿真模拟数学试卷（理工类）本试卷分第I卷（选择题）和第H卷（非选择题）两部分，共23题，共150分，共3页。

考试时间：120 分钟考试结束后，将本试卷和答题卡一并交回。

第I卷（共60分）一、选择题：本大题共12 个小题，每小题5 分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合，，则（）A. B. C. D.【答案】A【解析】由题知，，则．故本题答案选．2. 已知复数．若在复平面内对应的点分别为，线段的中点对应的复数为，则（）A. B. 5 C. D.【答案】A【解析】，所以，选A.3. 命题，则的否定形式是（）A. ，则B. ，则C. ，则D. ，则【答案】D【解析】试题分析：在变命题的否定形式的时候，要注意把全称命题改成特称命题，本题中需要改动两处：一处是全称量词“任意”改成存在量词“存在”，另外一处把“大于等于” 改成相反方面“小于” . 所以本题应该选D.考点：命题的否定形式.4. 已知等差数列的公差为2，若、、成等比数列，则等于（）A. －2B. －4C. 2D. 0【答案】C 【解析】由题知，即，又，解得，则．故本题答案选．5. 二项式的展开式中项的系数为，则（）A. 4B. 5C. 6D. 7答案】C【考点定位】二项式定理．6. 是表示空气质量的指数，指数值越小，表明空气质量越好，当指数值不大于100 时称空气质量为“优良”．如图是某地4月1日到12 日指数值的统计数据，图中点表示4 月1 日的指数值为201 ．则下列叙述不正确的是（）A. 这12天中有6天空气质量为“优良”B. 这12天中空气质量最好的是4月9 日C. 这12天的指数值的中位数是90D. 从4日到9 日，空气质量越来越好【答案】C【解析】由图可知，不大于100天有6日到11日,共6天，所以A对，不选.最小的一天为10日,所以B对,不选•中位为是,C错.从图中可以4日到9日越来越小，D对.所以选C.7. 高三某班15名学生一次模拟考试成绩用茎叶图表示如图1．执行图2 所示的程序框图，若输入的分别为这15 名学生的考试成绩，则输出的结果为（）A. 6B. 7C. 8D. 9【答案】D【解析】由框图功能可知，它的作用是统计出分数大于或等于110 分的人数n. 所以. 选D.8. 已知，是曲线与轴围成的封闭区域．若向区域内随机投入一点，则点落入区域的概率为（）A. B. C. D.【答案】D【解析】如下图，我们可知概率为两个面积比. 选D.【点睛】解几何概型问题的关键是确定“测度” ，常见的测度有长度、面积、体积等，若题中只有一个变量，可考虑利用长度模型，若题中由两个变量，可考虑利用面积模型.9. 设点在不等式组所表示的平面区域内，则的取值范围为（）A. B. C. D.【答案】D【解析】如图所示，绘制不等式组表示的平面区域，结合目标函数的几何意义可得，目标函数在点处取得最大值2，在点处取得最大值5，目标函数的取值范围是.本题选择D选项•10. 已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得出这个几何体的内切球半径是（）A. B. C. D.【答案】D【解析】由三视图可知，该几何体为三棱锥，设内切球半径为，则由棱锥的体积公式有①，其中，分别为三棱锥四个面的面积，，代入①得到，解得•11. 如图所示点是抛物线的焦点，点分别在抛物线及圆的实线部分上运动，且总是平行于轴，则的周长的取值范围是（）A. B.C. D.【答案】B【解析】抛物线的的准线方程，焦点，由抛物线的定义可得，圆的圆心，半径，所以的周长，由抛物线及圆可得交点的横坐标为，所以，所以，故选B.12. 已知函数f (X)=，若存在X i、X2、…X n满足==••==,贝U X1+X2+…+X n的值为( )A. 4B. 6C. 8D. 10答案】C解析】由函数的解析式可得函数f(x) 的图象关于点(2,0) 对称，结合图象知：X I、X2、…X n满足•••函数f (x)与y= x-1的图象恰有5个交点，且这5个交点关于(2,0)对称, 除去点(2,0) ，故有X1+X2 +…+ X n=X l+X2+X3+X4=8.本题选择C选项.第n卷(共90分)二、填空题(每题5 分，满分20 分，将答案填在答题纸上)13. 已知函数(为正实数)只有一个零点，则的最小值为【答案】【解析】函数只有一个零点，则，则，可知，又，则．故本题应填．点睛：本题主要考查基本不等式. 基本不等式可将积的形式转化为和的形式, 也可将和的形式转化为积的形式, 两种情况下的放缩功能, 可以用在一些不等式的证明中, 还可以用于求代数式, 函数等的取值范围或最值中. 与常用来和化积, 而和常用来积化和.14. 设直线过双曲线的一个焦点，且与的一条对称轴垂直，与交于、两点，为的实轴长的倍，则的离心率为________________ ．【答案】【解析】设双曲线的标准方程为，由题意，得，即，，所以双曲线的离心率为. 点睛：处理有关直线和圆锥曲线的位置关系问题时，记住一些结论可减少运算量、提高解题速度，如：过椭圆或双曲线的焦点且与焦点所在坐标轴垂直的弦长为，过抛物线的焦点且与对称轴垂直的弦长为.15. 把3 男生2女生共5名新学生分配到甲、乙两个班，每个班分的新生不少于2 名，且甲班至少分配1 名女生，则不同的分配方案种数为 _________________ ．(用数字作答)【答案】1616.已知函数，点O为坐标原点，点，向量=(0 , 1 ), 0 n是向量与的夹角，则使得恒成立的实数t 的取值范围为 ______________ ．【答案】【解析】根据题意得, 是直线OA n 的倾斜角，则：，据此可得：结合恒成立的结论可得实数t 的取值范围为.点睛：对于恒成立问题，常用到以下两个结论：⑴ a> f(X)恒成立？a> f(X)max；⑵ a< f (x)恒成立？a< f (x) min.用裂项相消法求和时，注意裂项后的系数以及搞清未消去的项，要注意正负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消去的项，未被消去的项有前后对称的特点，实质上造成正负相消是此法的根源与目的．三、解答题 (本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在中，角所对的边分别为•(1)求角；(2)若的中线的长为，求的面积的最大值.【答案】( 1 )； (2)．【解析】试题分析：(1) 由题意结合余弦定理求得；(2) 利用余弦定理结合面积公式和均值不等式可得的面积的最大值为．试题解析：(1) ，即.(2) 由三角形中线长定理得：，由三角形余弦定理得：，消去得: (当且仅当时，等号成立) ，即.18. (本小题满分12 分)电视传媒公司为了解某地区电视观众对某类体育节目的收视情况，随机抽取了100 名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：将日均收看该体育节目时间不低于40分钟的观众称为"体育迷”.（1）根据已知条件完成上面的列联表，若按的可靠性要求，并据此资料，你是否认为“体育迷”与性别有关？（2）将上述调查所得到的频率视为概率.现在从该地区大量电视观众中，采用随机抽样方法每次抽取1名观众，抽取3次，记被抽取的3名观众中的“体育迷”人数为.若每次抽取的结果是相互独立的，求分布列，期望和方差.附：【答案】（1）没有理由认为“体育迷”与性别有关；（2）分布列见解析，期望为，方差为.【解析】试题分析：（1）利用频率分布直方图，可得各组概率，进一步可填出列联表，利用公式求出的值，结合所给数据，用独立性检验可得结果；（2）利用分层抽样，可确定人中有男女，利用古典概型，可得结果.试题解析：（1）由频率分布直方图可知，在抽取的100人中，“体育迷”有25人，从而列联表如下：将列联表中的数据代入公式计算，得因为，所以没有理由认为“体育迷”与性别有关.（2）由分层抽样可知人中男生占，女生占，选人没有一名女生的概率为，故所求被抽取的2名观众中至少有一名女生的概率为.19.如图，在四棱锥P—ABCDK 平面PADL底面ABCD其中底面ABC［为等腰梯形，AD// BCPA= AB= BC= CD= 2, PD= 2, PAL PD Q为PD的中点.(I)证明：CQ/平面PAB(n)求直线PD与平面AQC所成角的正弦值【答案】(I)见解析；(n).【解析】试题分析：⑴取PA的中点N,由题意证得BN// CQ则CQ/平面PAB⑵利用题意建立空间直角坐标系，结合平面的法向量可得直线PD与平面AQC所成角的正弦值为．试题解析：(I)证明如图所示，取PA的中点N,连接QNBN 在^ PAD中, PNh NA PQ= QD所以QN/ AD 且QNh AD在厶APD中 , PA^ 2 , PD= 2, PA± PD所以AD== 4,而BC= 2,所以BC= AD又BC// AD,所以QN/ BC 且QNh BC故四边形BCQ为平行四边形，所以BN// CQ又BN?平面PAB且CQ平面PAB 所以CQ/平面PAB(n)如图，取AD的中点M连接BM取BM的中点Q连接BO PO由(1)知PA= AM= PM= 2,所以△ APM为等边三角形，所以POL AM 同理BOL AM.因为平面PADL平面ABCD所以POh BO.如图，以O为坐标原点，分别以OB OD OP所在直线为x轴，y轴，z轴建立空间直角坐标系则O(0,0,0) D(0,3,0) A(0 －1,0) B( 0,0) P(0,0 ) C( 2,0)则=(,3,0).因为Q为DP的中点，故Q所以=.设平面AQC的法向量为m= (x , y , z),则可得令y =—，贝U x= 3, z = 5.故平面AQC勺一个法向量为m^ (3，—, 5).设直线PD与平面AQC所成角为0.贝U sin 0 = |cos 〈，n〉| ==.从而可知直线PD与平面AQC所成角正弦值为.20. 已知分别是椭圆勺左，右焦点，分别是椭圆勺上顶点和右顶点，且，离心率.(I)求椭圆的方程；(H)设经过的直线与椭圆相交于两点，求的最小值【答案】(I) ； (n).【解析】试题分析：(1) 由题意列方程可得，故所求椭圆方程为(2) 设出直线方程，联立直线与椭圆的方程，结合题意可得，当且仅当时上式取等号. 的最小值为。

大庆实验中学2020届高三综合训练（三）数学试卷参考答案1．已知集合{|A x y ==，{}2|76<0B x x x =-+，则()R C A B ⋂=（）A ．{}|1<<3x x B ．{}|1<<6x x C ．{}|13x x ≤≤D ．{}|16x x ≤≤【答案】A 【详解】解：{|A x y ==={}|30x x -≥={}|3x x ≥，即{}|3R C A x x =<，又{}2|76<0B x x x =-+={}|(1)(6)<0x x x --={}|16x x <<，即()R C A B ⋂={}|1<<3x x ，故选A.2．i 是虚数单位，复数z =，则（）A ．1322z -=B ．34z =C ．3322z i =-D ．3344z i =+【答案】D 【详解】3333444z i +===+1122z -=，3||2z =故选：D 3．下列命题中是真命题的是（）①“1x >”是“21x ”的充分不必要条件；②命题“0x ∀>，都有sin 1x ”的否定是“00x ∃>，使得0sin 1x >”；③数据128,,,x x x 的平均数为6，则数据12825,25,,25x x x --- 的平均数是6；④当3a =-时，方程组232106x y a x y a-+=⎧⎨-=⎩有无穷多解.A ．①②④B ．③④C ．②③D ．①③④【答案】A【详解】①1x >，则有21x ≥，但21x ≥，则1x >或1x <-，所以“1x >”是“21x ≥”的充分不必要条件，所以①正确；②命题“0x ∀>，都有sin 1x ≤”的否定是“00x ∃>，使得0sin 1x >”，所以②正确；③由()6E X =，可得(25)2()52657E X E X -=-=⨯-=，故③错误；④当3a =-时，26a x y a -=即为963x y -=-，即3210x y -+=，所以方程组232106x y a x y a -+=⎧⎨-=⎩有无穷多解，④正确.故选：A.4．二项式261(2x x-的展开式中3x 的系数为（）A ．52-B ．52C ．1516D ．316-【答案】A 【详解】通项为()()6212316611122rrrr r r rr T Cx C x x --+⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭令1233r -=，则3r =，()333334615122T C x x ⎛⎫=-=- ⎪⎝⎭故选：A5．设不等式组00x y x +≥⎧⎪⎨-≤⎪⎩表示的平面区域为Ω，若从圆C ：224x y +=的内部随机选取一点P ，则P 取自Ω的概率为（）A ．524B ．724C ．1124D ．1724【答案】B【详解】作出Ω中在圆C 内部的区域，如图所示，因为直线0x y +=，0x -=的倾斜角分别为34π，6π，所以由图可得P 取自Ω的概率为3746224πππ-=.故选：B 6．马拉松是一项历史悠久的长跑运动，全程约42千米.跑马拉松对运动员的身体素质和耐力是极大的考验，专业的马拉松运动员经过长期的训练，跑步时的步幅（一步的距离）一般略低于自身的身高，若某运动员跑完一次全程马拉松用了2.5小时，则他平均每分钟的步数可能为（）A ．60B ．120C ．180D ．240【答案】C 【详解】解：42千米＝42000米，2.5小时＝150分钟，故运动员每分钟跑42000150280÷=米；若运动员每分钟跑120步，280120 2.33÷=，则运动员的身高超过2.33米不太可能；若运动员每分钟跑240步，280240 1.17÷=，则运动员的身高稍超过1.17米不太可能；若运动员每分钟跑180步，280180 1.56÷=，则运动员的身高超过1.56米，基本符合实际，故选：C .7．已知m ，n 是两条不重合的直线，α，β是两个不重合的平面，则下列命题中错误的是（）A ．若m //α，α//β，则m //β或m β⊂B ．若m //n ，m //α，n α⊄，则n //αC ．若m n ⊥，m α⊥，n β⊥，则αβ⊥D ．若m n ⊥，m α⊥，则n //α【答案】D【详解】选项A ：若m //α，α//β，根据线面平行和面面平行的性质，有m //β或m β⊂，故A 正确；选项B ：若m //n ，m //α，n α⊄，由线面平行的判定定理，有n //α，故B 正确；选项C ：若m n ⊥，m α⊥，n β⊥，故α，β所成的二面角为090，则αβ⊥，故C 正确；选项D ，若m n ⊥，m α⊥，有可能n ⊂α，故D 不正确.故选：D 8．设函数1()ln1xf x x x+=-，则函数的图像可能为（）A ．B ．C ．D ．【答案】B 【详解】1()ln1xf x x x+=-定义域为：(1,1)-11()lnln ()11x xf x x x f x x x-+-=-==+-，函数为偶函数，排除,A C 11()22ln 30f =>，排除D 故选B 9．框图与程序是解决数学问题的重要手段，实际生活中的一些问题在抽象为数学模型之后，可以制作框图，编写程序，得到解决，例如，为了计算一组数据的方差，设计了如图所示的程序框图，其中输入115x =，216x =，318x =，420x =，522x =，624x =，725x =，则图中空白框中应填入（）A ．6i >，7S S =B ．6i 7SS =C ．6i >，7S S =D ．6i ，7S S=【答案】A 【详解】根据题意为了计算7个数的方差，即输出的()()()22212712020207S x x x ⎡⎤=-+-+⋯+-⎣⎦，观察程序框图可知，应填入6i >，7SS =，故选：A.10．已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右两个焦点分别为1F ，2F ，若存在点P 满足1212::4:6:5PF PF F F =，则该双曲线的离心率为（）A ．2B ．52C ．53D ．5【答案】B【详解】122155642F F e PF PF ===--.选B.11．已知抛物线C ：24x y =的焦点为F ，过点F 的直线l 交抛物线C 于A ，B 两点，其中点A 在第一象限，若弦AB 的长为254，则AF BF =（）A ．2或12B ．3或13C ．4或14D ．5或15【答案】C 【详解】设直线的倾斜角为θ，则222425cos cos 4p AB θθ===，所以216cos 25θ=，2219tan 1cos 16θθ=-=，即3tan 4θ=±，所以直线l 的方程为314y x =±+.当直线l 的方程为314y x =+，联立24314x yy x ⎧=⎪⎨=+⎪⎩，解得11x =-和24x =，所以()40401AF BF -==--；同理，当直线l 的方程为314y x =-+.14AF BF =，综上，4AF BF =或14.选C.12．已知四棱锥P ABCD -的四条侧棱都相等，底面是边长为2的正方形，若其五个顶点都在一个表面积为814π的球面上，则PA 与底面ABCD 所成角的正弦值为（）A ．23B ．23或3C．3D ．13或3【答案】D【详解】因为P ABCD -的四条侧棱都相等，底面是边长为2的正方形，则点P 在面ABCD 内的射影落在正方形ABCD 的中心，连接,AC BD 交于点E ，设球心为O ,连接,PO BO ,则E 在直线PO 上，PO BO R ==，由28144R ππ=,解得94R =，又2BDBE ==所以74OE==,所以971442PE R OE=-=-=或97444PE R OE=+=+=，当12PE=时，32PA==,则PA与底面ABCD所成角的正弦值为112332PEAP==,当4PE=时，PA===则PA与底面ABCD所成角的正弦值为3PEAP==,即PA与底面ABCD所成角的正弦值为13或3，故选D.13．已知平面向量a与b的夹角为3π，1)a=-，1b||=，则|2|a b-=________.【详解】由1)a=-可得||2a==，则||||cos13a b a bπ⋅=⋅=，所以|2|a b-===故答案为:14．已知各项均为正数的等比数列{}n a的前n项积为n T，484a a=，1122log3bT=（0b>且1b≠），则b=__________.【答案】由于0na>，24864a a a⋅==，所以62a=，则11111162T a==，∴1122log11log23b bT=⨯=，2log23b=，233b==故答案为：15．某三棱锥的三视图如图所示，且图中的三个三角形均为直角三角形，则x y+的最大值为________.【答案】16【详解】由三视图之间的关系可知2210802x y=--,整理得22128x y+=,故22222()2()2562xx y x y x yy=++=++≤,解得16x y+,当且仅当8x y==时等号成立,故答案为:1616．已知曲线1C ：()2xf x e x =--，曲线2C ：()cosg x ax x =+，（1）若曲线1C 在0x =处的切线与2C 在2x π=处的切线平行，则实数a =________；（2）若曲线1C 上任意一点处的切线为1l ，总存在2C 上一点处的切线2l ，使得12l l ⊥，则实数a 的取值范围为________.【答案】－21,12⎡⎤-⎢⎥⎣⎦【详解】(1)()2x f x e '=--,则曲线1C 在0x =处的切线的斜率1(0)3k f '==-,2()sin ,g x a x C '=-在2x π=处的切线的斜率212k g a π⎛⎫'==- ⎪⎝⎭,依题意有13a -=-,即2a =-;(2)曲线1C 上任意一点处的切线的斜率1()2xk f x e '==--,则与1l 垂直的直线的斜率为110,22x e ⎛⎫∈ ⎪+⎝⎭,而过2C 上一点处的切线的斜率[]2()sin 1,1k g x a x a a '==-∈-+,依题意必有10112a a -≤⎧⎪⎨+≥⎪⎩,解得112a -≤≤,故答案为:12;,12⎡⎤--⎢⎥⎣⎦.17．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c 且()()()sin sin sin c a C A a b B -+=+，2sin sin cos 2CA B =，（1）求C ；（2）若ABC的面积为c ．解：（1）()()()sin sin sin c a C A a b B -+=+ ，由正弦定理得:()()()c a c a a b b -+=+，∴222a b c ab +-=-，又由余弦定理得：222cos 2a b c C ab+-=，1cos 22ab C ab -∴==-，即：1cos 2C =-，∵0C π<<，∴23C π=.（2）因为21cos sin sin cos 22C C A B +==，所以()2sin cos 1cos 1cos A B C πA B =-=+-+⎡⎤⎣⎦()1cos 1cos cos sin sin A B A B A B=-+=-+化简得()cos 1A B -=，∵23C π=，则A ，0,3B π⎛⎫∈ ⎪⎝⎭，∴33ππA B -<-<，∴0A B -=，得：A B =，因为ABC的面积为，所以212sin 234πS ab a ===，得216a =，∴4a b ==由余弦定理知：2222212cos 44244482c a b ab C ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭，∴c =18．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形//AB CD ，AB AD ⊥，PA ⊥平面ABCD ，E 是棱PC 上的一点.（1）证明：平面ADE ⊥平面PAB ；（2）若PE EC λ=，F 是PB的中点，AD =，22AB AP CD ===，且二面角F AD E --的正弦值为10，求λ的值.【详解】(1)因为PA ⊥平面ABCD ,AD ⊂平面ABCD ,所以PA AD ⊥,又AB AD ⊥,PA AB A = ,所以AD ⊥平面PAB ,又AD ⊂平面ADE ,所以平面ADE ⊥平面PAB ;(2)以A 为原点,AD ,AB ,AP 分别为x ,y ,z 轴,建立如图所示的空间直角坐标系:则(0,0,0)A ,(0,2,0)B ,(0,0,2)P,C,D ,(0,1,1)F ,由(1)知AD ⊥平面PAB ,故AD PB ⊥,又F 是PB 的中点,AB AP =,∴PB AF ⊥,且AF A AD = ,∴PB ⊥平面ADF ,∴平面ADF 的一个法向量为(0,2,2)PB =-,∵PE EC λ=,∴2,,1111PE PC λλλλλλλ⎛⎫-== ⎪ ⎪++++⎝⎭ ,∴2,,111AE AP PE λλλλ⎛⎫=+= ⎪ ⎪+++⎝⎭,设平面ADE 的法向量为(,,)n x y z = ,则0n AD ⋅=且0n AE ⋅=r uu u r ,0=且20111x y zλλλλλ++=+++,∴0x =,令1y =,则2z λ=-,∴平面ADE 的一个法向量0,1,2n λ⎛⎫=- ⎪⎝⎭ ,∵二面角F AD E --的正弦值为10,∴()cos ,10PB n = ,31010=,∴1λ=或4.19．甲、乙两位同学参加某个知识答题游戏节目，答题分两轮，第一轮为“选题答题环节”第二轮为“轮流坐庄答题环节”.首先进行第一轮“选题答题环节”，答题规则是：每位同学各自从备选的5道不同题中随机抽出3道题进行答题，答对一题加10分，答错一题（不答视为答错）减5分，已知甲能答对备选5道题中的每道题的概率都是23，乙恰能答对备选5道题中的其中3道题；第一轮答题完毕后进行第二轮“轮流坐庄答题环节”，答题规则是：先确定一人坐庄答题，若答对，继续答下一题…，直到答错，则换人（换庄）答下一题…以此类推.例如若甲首先坐庄，则他答第1题，若答对继续答第2题，如果第2题也答对，继续答第3题，直到他答错则换成乙坐庄开始答下一题，…直到乙答错再换成甲坐庄答题，依次类推两人共计答完20道题游戏结束，假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答，且记第n 道题也由该同学（最先答题的同学）作答的概率为n P （120n ≤≤），其中11P =，已知供甲乙回答的20道题中，甲，乙两人答对其中每道题的概率都是13，如果某位同学有机会答第n 道题且回答正确则该同学加10分，答错（不答视为答错）则减5分，甲乙答题相互独立；两轮答题完毕总得分高者胜出.回答下列问题（1）请预测第二轮最先开始作答的是谁？并说明理由（2）①求第二轮答题中2P ，3P ；②求证12n P⎧-⎫⎨⎬⎩⎭为等比数列，并求n P （120n ≤≤）的表达式.【详解】(1)设甲选出的3道题答对的道数为ξ,则23,3~B ξ⎛⎫ ⎪⎝⎭,设甲第一轮答题的总得分为x ,则105(3)1515x ξξξ=--=-,所以2151515315153Ex E ξ=-=⨯⨯-=;(或法二:设甲的第一轮答题的总得分为x ,则x 的所有可能取值为30,15,0,-15,且33328(30)327P x C ⎛⎫=== ⎪⎝⎭,2231212(15)3327P x C ⎛⎫=== ⎪⎝⎭,213126(0)3327P x C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,30311(15)327P x C ⎛⎫=-== ⎪⎝⎭,故得分为x 的分布列为:x30150-15812130151515272727Ex =⨯+⨯-⨯=;设乙的第一轮得分为y ,则y 的所有可能取值为30,15,0,则33351(30)10C P y C ===,2132356(15)10C C P y C ===,1232353(0)10C C P y C ===,故y 的分布列为:x30150P110610310故163015121010Ey =⨯+⨯=,∵Ex Ey >,所以第二轮最先开始答题的是甲.(2)①依题意知11P =,213P =,31122533339P =⨯+⨯=,②依题意有()111121213333n n n n P P P P ---=⨯+-⨯=-+(2n ≥),∴1111232n n P P -⎛⎫-=-- ⎪⎝⎭,(2n ≥),又11122P -=,所以12n P ⎧-⎫⎨⎬⎩⎭是以12为首项,13-为公比的等比数列,∴1111223n n P -⎛⎫-=⨯- ⎪⎝⎭,∴1111223n n P -⎛⎫=+⨯- ⎪⎝⎭(120n ≤≤).20．如图，设F 是椭圆2222:1(0)x y C a b a b +=>>的左焦点，直线：2a x c=-与x轴交于P 点，AB 为椭圆的长轴，已知8AB=，且2PA AF =，过P 点作斜率为k 直线l 与椭圆相交于不同的两点M N 、，（1）当14k =时，线段MN 的中点为H ，过H 作HG MN ⊥交x 轴于点G ，求GF ；（2）求MNF ∆面积的最大值.【详解】（1）∵8AB =,∴4a =，又∵2PA AF =，即()2222310aa a c e e c -=-⇒-+=∴12e =∴2c =,22212b a c =-=∴椭圆的标准方程为2211612x y +=点P 的坐标为()8,0-，点F 的坐标为()2,0-直线l 的方程为()184y x =+即48x y =-联立224811612x y x y =-⎧⎪⎨+=⎪⎩可得21348360y y -+=，设()()1122,,M x y N x y ，()00,H x y 则124813y y +=，123613y y =所以12024213y y y +==，0024848481313x y =-=⨯-=-直线HG 的斜率为4-，直线HG 的方程为24841313y x ⎛⎫-=-+ ⎪⎝⎭令0y =，解得213x =-即2,013G ⎛⎫- ⎪⎝⎭所以22421313G F GF x x ⎛⎫=-=---= ⎪⎝⎭（2）直线l 的方程为()8y k x =+，当0k =时，三角形不存在当0k ≠时，设1m k=，直线l 的方程为8x my =-联立22811612x my x y =-⎧⎪⎨+=⎪⎩可得()2234481440m y my +-+=，设()()1122,,M x y N x y ()()()2224843414457640m m m ∆=--+⨯=->，解得2m >或2m <-1224834m y y m +=+，12214434y y m =+222248144143434m MN m m m ⎛⎫=+⋅-⨯ ⎪++⎝⎭222241434m m m +⋅-=+点F 到直线l 的距离2228611d m m -==++2211223434MNFm m m S MN d m m ∆=⋅=⨯=++7216=≤=当且仅当=m =时（此时适合于△＞0的条件）取等号,所以当114k m ==±时，直线l为()814y x =±+时，MNF ∆面积取得最大值为21．已知函数()()1ln 1f x x x =++，()ln 1x g x e x -=++（1）讨论()f x 的单调性；（2）设()()()h x f x g x =-，若()h x 的最小值为M ，证明：2211M e e--<<-.【详解】(1)()()1ln 1ln ln 1f x x x x x x =++=++()1ln 1f x x x+'=+，设()()221111ln 1,x m x x m x x x x x-=++=-='()01m x x >'⇒>；()001m x x <⇒<<'所以()m x 在()0,1上单调递减，在()1,+¥上单调递增()()min 120m x m ==>，即()0f x ¢>所以()f x 在()0,+¥上单调递增(2)()()()()1ln ln ln x xh x f x g x x x e x x x e --=-=+--=-()ln 1x h x e x -=++'，设()ln 1x F x e x -=++()11x x x e x F x e x xe='-=-+，设()x G x e x =-()10x G x e ='->，所以()G x 在()0,+¥上单调递增()()010G x G >=>，即()0F x '>，所以()F x 在()0,+¥上单调递增()()12120,10e e F e e F e e ------=>=-<所以()F x 在()0,+¥上恰有一个零点()210,x e e --∈且()00ln 10*x e x -++=()h x 在()00,x 上单调递减，在()0,x +∞上单调递增()00000001ln ln ln 1x M h x x x x x x e ==-=++，()210,x e e --∈由（1）知()0f x 在()0,+¥上单调递增所以()()()2102211f e f x f e e e ----=<<=-所以2211M e e --<<-22．在平面直角坐标系xOy 中，已知直线l的参数方程为1222x t y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数），以坐标原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为4πρθ⎛⎫=+⎪⎝⎭．（1）求直线l 的普通方程和曲线C 的直角坐标方程；（2）设点()2,1P ，直线l 与曲线C 的交点为A 、B ，求PA PB PB PA+的值．【详解】解：（1）l 的参数方程消去参数，易得l 的普通方程为10x y --=，曲线C：()2cos sin 2πρθθθ⎛⎫=+=+ ⎪⎝⎭，即()22cos sin ρρθθ=+，∴22220x y x y +--=，所以曲线C 的直角坐标方程为：22220x y x y +--=.（2）l的参数方程22,21,2x t y t ⎧=+⎪⎪⎨⎪=+⎪⎩（t 为参数），设A 对应参数为1t ，B 对应参数为2t ，将l 的参数方程与22220x y x y +--=联立得：210t +-=，得：12t t +=，121t t ⋅=-，所以2212122112PA PBt t t t PB PAt t t t ++=+=()()2212121221222411t t t t t t -⨯-+-+====-即4PA PBPB PA +=.23．设a 、b 、c 均为正数，（Ⅰ）证明：222a b c ab bc ca ++≥++；（Ⅱ）若1ab bc ca ++=，证明a b c ++≥.【详解】（Ⅰ）因为a ，b ，c 均为正数，由重要不等式可得222a b ab +，222b c bc +，222c a ca +，以上三式相加可得222222222a b b c c a ab bc ca +++++++，即222a b c ab bc ca ++++；（Ⅱ）因为1ab bc ca ++=，由（Ⅰ）可知2221a b c ++，故2222()222123a b c a b c ab bc ca ++=++++++=，所以a b c ++得证．。

绝密★启用前2020届黑龙江省实验中学高三下学期开学考试数学（理）试题注意事项：1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上 一、单选题1.已知集合⎭⎬⎫⎩⎨⎧≤≤=4241|x x A ，{}x x y y B -+-==22|，则=⋂B A ()A.{}0B.{}2C.[-2,2]D.[0,2] 2.给定下列三个命题：1:p 函数x y a a =+（0a >且1a ≠）在R 上为增函数； 222:,0p a b R a ab b ∃∈-+<，；3:cos cos p αβ=成立的一个充分不必要条件是2()k k Z απβ=+∈.其中的真命题为（）A ．12p p ∨B ．23p p ∧C ．13p p ∨⌝D ．23p p ⌝∧3.l 、m 、n 表示空间中三条不同的直线，α、β表示不同的平面，则下列四个命题中正确的是（）A ．若m α⊂，n β⊂，//αβ，则//m nB ．若m α⊂，n β⊂，//m β，//n α，则//αβC ．若l αβ=，m α⊂，n β⊂，l m ⊥，l n ⊥，则αβ⊥D ．若m α⊂，n β⊂，m β⊥，n α⊥，则αβ⊥4.已知,为互相垂直的单位向量，若-=，则=（）A.22-B.22C.33-D.335.01(e )d x x x --=⎰（）A ．11e --B ．1-C ．312e-+D ．32-6.设x,y,z 是互不相等的正数，则下列不等式中不恒成立的是（）A ．2211x x x x++≥B C ．12x y x y-+≥-D ．x y x z y z -≤-+-7.在ABC ∆中，A ，B ，C 所对的边分别为a,b,c ，若060=A ,3=a ，3=+c b ，则ABC ∆的面积为（） A.43B.23C.3D.2 8.在平面直角坐标系xOy 中，已知2111ln 0x x y --=，2220x y --=，则()()221212x x y y -+-的最小值为() A ．1B ．2C ．3D ．49.算筹是在珠算发明以前我国独创并且有效的计算工具，为我国古代数学的发展做出了很大贡献.在算筹计数法中，以“纵式”和“横式”两种方式来表示数字，如图：表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用横式，以此类推，遇零则置空，如图：如果把5根算筹以适当的方式全部放入下面的表格中，那么可以表示的三位数的个数为（）A ．46B ．44C ．42D ．4010.抛物线)0(22>=p px y C ：的焦点为F ，抛物线C 与圆()33:221=-+y x C 交于M,N两点，若6|=MN |，则MNF ∆的面积为（）A.423B.823C.83D.8211.在内接于球O 的四面体ABCD 中,有AB CD t ==,6AD BC ==,7AC BD ==,若球O 的最大截面的面积是554π,则t 的值为() A ．5B ．6C ．7D ．812.已知函数()()R a x a x x x f ∈--=1ln )(22，若()0≥x f 在1x 0≤<上恒成立，则实数a 的取值范围是（） A.),42[+∞ B.),21[+∞C.),1[+∞D.),2[+∞ 二、填空题 （13）若复数()()1a i i ++在复平面上所对应的点在实轴上，则实数a =______.（14）现有高一学生两人，高二学生两人，高三学生一人，将这五人排成一行，要求同一年级的学生不能相邻，则不同的排法总数为（15）已知直线x y -=1与双曲线()0,0122<>=+b a by ax 的渐近线交于A,B 两点，且过原点和线段AB 中点的直线的斜率为23-，则=ab （16）观察下面的数表，该表中第6行最后一个数是______（2分）；设2016是该表的m 行第n 个数，则m n +=______（3分）.三、解答题17.（10分）在平面直角坐标系y x 0中，直线l 的参数方程为()为参数t t y t x ⎩⎨⎧+=-=3,1，以为极点，x 轴的正半轴为极轴建立极坐标系，曲线1C 的极坐标方程为ϕρcos 2=，点P 是曲线1C 上的动点，点Q 在OP 的延长线上且|PQ|=3|OP|,点Q 的轨迹为2C . （1）求直线l 及曲线2C 的极坐标方程。

2．在复平面内，复数2 - 3i3+ 2i+ z对应的点的坐标为( )，则z在复平面内对应的点位于（）②已知相关变量ሼ满足回归方程ሼ集，若变量增加一个单位，则ሼ平均增加个单位；③对分类变量X与Y，若它们的随机变量K2的观测值k越小，则判断“X与Y 有关系”的犯错误的概率越小；④用系统抽样的方法先从高三年级的2000名学生中抽取一个容量是40 的样本，先将总体编号：1到2000，再从编号为1 到50的学生中随机抽取1名学生，若其编号为26，则抽取的第 5名学生编号为220．其中不正确说法的个数是( )A. 1B. 2C. 3D. 49．已知函数( ) = sin x -λcos x的一个对称中心为,0⎫⎪⎭，若将函数( )图象上点的纵坐标不变，横坐标缩小到原来的1，再将所得图象向右平移π3 -2，c＝4⎰递增区间是（）A. a>c>bB. b>a>cC. a>b>cD. c>b>a4．大衍数列，来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数量总和，是中华传统文化中隐藏着的世界数学史上第一道数列题.其规律是：偶数项是序号平方再除以2，奇数项是序号平方减1再除以2，其前10项依次是0，2，4，8，12，18，24，32，40，50，…，如图所示的程序框图是为了得到大衍数列的前100项而设计的，那么在两个“◇”中，可以先后填入（）A. 是偶数，B. 是奇数，C. 是偶数，D. 是奇数，‸ͲͲ5．如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体的三视图，则该几何体的体积为( )10．《红海行动》是一部现代化海军题材影片，该片讲述了中国海军“蛟龙突击队”奉命执行撤侨任务的故事.撤侨过程中，海军舰长要求队员们依次完成六项任务，并对任务的顺序提出了如下要求：重点任务A必须排在前三位，且任务E、F必须排在一起，则这六项任务的不同安排方案共有( )A. 240种B. 188种C. 156种D. 120种46．已知( )5 = a0 x5+a1x + ⋅⋅⋅⋅⋅⋅+a4 x + a5 ，则a0 + a1 + ⋅⋅⋅⋅⋅⋅+ a5 =（）A. 1B. 243C. 32D. 2117．若张三每天的工作时间在6小时至9小时之间随机均匀分布，则张三连续两天平均工作时间不少于7小时的概率是（）A. B. C. D.8．给出以下四个说法：①已知随机变量，，若쳌䁠集Ͳ，则䁠集ͲǤ；12．已知函数( ) = x + ln ( )图像上三个不同点, B,C的横坐标成公差为1 的等差数列，则二、填空题13．有6名学生参加数学竞赛选拔赛，他们的编号分别是1—6号，得第一名者将参加全国数学竞赛. 今有甲，乙，丙，丁四位老师在猜谁将得第一名，甲猜：4号，5号，6号都不可能；乙猜：3号不可ͲͲ一、选择题A. B. C. D.A. 第一象限B. 第二象限C. 第三象限D. 第四象限3．已知a＝2 -1，b＝(2log 2 3 )2, 2-大庆实验中学 2020 年高三得分训练（二）理科数学试题1 π 1(sinπ x)dx，则实数a，b，c的大小关系是( )f x3π⎛⎝f xg x g x2 12个单位，得到函数( )的图象，则( )的单调‸ͲͲ‸ͲͲ‸ͲͲ2⎡ ⎤⎢ ⎥⎣ ⎦ 2⎤⎥ ⎦2⎡ ⎤⎢ ⎥⎣ ⎦ 2⎤⎥ ⎦A. 2kπ ,2kπ + ,k ∈ ZB. 2kπ + ,2kπ +π ,k ∈ ZC. kπ ,kπ + ,k ∈ ZD. kπ + ,kπ +π ,k ∈ Zππ ππ3f x mx nx m+ + +ym n+11．已知函数( ) = x 3 2 2 在x = -1时有极值0，则椭圆x 2 22 2= 1的离心率为（）2 2 77 2 2 或77 22 1x -‸A.23B.43C.83D.4A.3B.9C.3 9D.9大庆实验中学得分训练（二）理数第 1 页共2 页1xf x e + A1e + 211ee++e +1 ( )2 1+ e2 2( )∆ABC面积的最大值为（）C. ln1+ eD. ln( )2A. ln2 eB. ln4e16．抛物线y2= 2px(p > 0)的焦点为F，准线为l，A、B是抛物线上的两个动点，且满足∠AFB =设线段AB的中点M在l上的投影为N，则MN的最大值是__________．三、解答题Sn⎫是等差数列，已知S2S3S4π3.19．如图，四棱锥H - ABCD中，HA ⊥底面ABCD，AD / /BC，AB = AD = AC = 6 ，HA = BC = 8 ， E 为线段AD 上一点，AE = 2ED，F 为HC的中点. （1）证明：EF / /平面HAB；（2）求二面角E - HF - A的正弦值.20．已知菱形形，在ሼ轴上且Ͳ‸，쳌‸（쳌Ͳ，쳌）．（Ⅰ）求点轨迹的方程；（Ⅱ）延长交轨迹于点，轨迹在点处的切线与直线交于点，试判断以为圆心，线段为半径的圆与直线的位置关系，并证明你的结论．n2 2（1）求{ }的通项公式；l : y = -3 3是曲线y = f ( )的的一条切线.18．某教育培训中心共有25名教师，他们全部在校外住宿.为完全起见，学校派专车接送教师们上下班.这个接送任务承包给了司机王师傅，正常情况下王师傅用34座的大客车接送教师.由于每次乘车人数不尽相同，为了解教师们的乘车情况，王师傅连续记录了100次的乘车人数，统计结果如下：乘车人数频数 2 4 4 10 16 20 16 12 8 6 2以这100次记录的各乘车人数的频率作为各乘车人数的概率.（Ⅰ）若随机抽查两次教师们的乘车情况，求这两次中至少有一次乘车人数超过18的概率；（Ⅱ）有一次，王师傅的大客车出现了故障，于是王师傅准备租一辆小客车来临时送一次需要乘车的教师.可供选择的小客车只有20座的A型车和22座的B型车两种，A型车一次租金为80元，B型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数，王师傅还要付给多出的人每人 20 元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据，判断王师傅租哪种车较合算？（1）求a的值；（2）设函数( ) ( ) - a+2，证明：函数( )无零点.22．选修4-4：坐标系与参数方程=1+ cosϕ（其中ϕ 为参数），曲线C2 : =1 .= sinϕ（2）射线l :θ =α ( )与曲线1、 2 分别交于点A B（且A B均异于原点O），当0 <大庆实验中学得分训练（二）理数第 2 页共2页an nS a= - { 2 log n aAB15．已知数列{ }满足2 4 1，当n∈ N*时，( )的取值范围是__________．2 + λlog2an} 是递增数列，则实数λ能；丙猜：不是1号就是2号；丁猜：是4号，5号，6号中的某一个.以上只有一个人猜对，则他应该是__________．14．在空间直角坐标系O - xyz中，正四面体P - ABC的顶点A、B分别在x轴，y轴上移动．若该正四面体的棱长是2，则OP 的取值范围是__________．a S2 3 417．设数列{ }的前n项和是n ，且⎧⎨⎩⎬⎭a1=1，+ + = 6 .形形形lnx x a x a R= + - ∈21 ．已知函数 f ( ) ( ) ( ) ，直线aaaln3x + - x2+ b Tan +1 n+2（2）若bn=an +2 n+1- 2，求数列{ }的前n项和n .15 16 17 18 19 20 21 22 23 24 25 在直角坐标系xOy中，曲线C1的参数方程为{x yxg x xe x f x a= - - - g x+x2y28 4ρ ≥ C C 、、|OA-以原点O为极点，x轴的正半轴为极轴建立极坐标系.（1）求曲线C1、C2的极坐标方程；α <π22 2时，求OB | 的最小值.。

2020年黑龙江省大庆实验中学高考数学综合训练试卷(理科)(三)一、选择题（本大题共12小题，共60.0分）1.设集合A={x|y=√1−x}，B={x|(x+1)(x−3)<0}，则(∁ R A)∩B=()A. [1,3)B. (1,3)C. (−1,0]∪[1,3)D. (−1,0]∪(1，3)2.已知复数z=2−1+i，则()A. z的虚部为−1B. z的实部为1C. |z|=2D. z的共轭复数为1+i3.命题“∀x∈R，都有|sinx|<1”的否定是()A. ∀x∈R，都有|sinx|>1B. ∀x∈R，都有|sinx|≥1C. ∃x∈R，使|sinx|>1D. ∃x∈R，使|sinx|≥14.(x+ y2x)(x+y)5的展开式中x3y3的系数为()A. 5B. 10C. 15D. 205.设不等式组{x+y≥0,x−√3y≤0表示的平面区域为Ω，若从圆C：x2+y2=4的内部随机选取一点P，则P取自Ω的概率为()A. 524B. 724C. 1124D. 17246.甲乙两名运动员在某项测试中的8次成绩如茎叶图所示，则甲运动员的极差与乙运动员的众数分别是()A. 20、80B. 20、81C. 17、80D. 17、817.已知两条不同的直线l，m和两个不同的平面α，β，下列四个命题中错误的为()A. 若l//α，l⊥β，则α⊥βB. 若α//β，m⊥α，则m⊥βC. 若α∩β=m，l//α且l//β，则l//mD. 若α//β，m//α，则m//β8. 函数f (x )=(x −1)lnx 2的图象大致为( )A.B.C.D.9. 如图所示的程序框图，若输出的y =−6，则输入的x 值为( )A. −92 B. 12 C. 32 D. −92或1210. 设双曲线C ：x 2a 2−y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1、F 2，点P 在C 上，且满足|PF 1|=3a ，若满足条件的点P 只在C 的左支上，则C 的离心率的取值范围是( )A. (1,2]B. (2,+∞)C. (2,4]D. (4,+∞)11. 设抛物线C ：y 2=4x 的焦点为F ，直线l 过F 且与抛物线C 交于A ，B 两点，若|AB|=163，且|AF|>|BF|，则|AF||BF|=( )A. 3B. 52C. 2D. 412. 已知正四棱锥S −ABCD 的五个顶点在表面积为25π3的同一球面上，它的底面边长为2，则它的侧棱与底面所成角的正弦值为( )A. √155B. √105C. 15D. √612二、填空题（本大题共4小题，共20.0分）13.平面向量a⃗与b⃗ 的夹角为120°，a⃗=(2,0)，|b⃗ |=1，则|a⃗−2b⃗ |=______ ．14.各项均为正数的等比数列{a n}的前n项和为S n，已知S3=10，S6=30，则S12=________．15.某三棱锥的三视图如图所示，且图中的三个三角形均为直角三角形，则x+y的最大值为________．16.曲线f(x)=e x在x=0处的切线方程为______ ．三、解答题（本大题共7小题，共82.0分）17.已知a，b，c分别为△ABC的三个内角A，B，C的对边，且．(1)求角A；(2)若a=2√3，△ABC的面积为√3，求b，c．18.如图，在四棱锥P−ABCD中，PC⊥底面ABCD，底面ABCD是直角梯形，AB//CD，AB⊥AD，AB=2AD=2CD=2，E是PB上的一点．(Ⅰ)求证：平面EAC⊥平面PBC；(Ⅱ)若E是PB的中点，PC>AC，且直线PA与平面EAC所成角的正弦值为√2，求二面角P−AC−3E的余弦值．19.甲、乙两位同学参加某个知识答题游戏节目，答题分两轮，第一轮为“选题答题环节”，第二轮为“轮流坐庄答题环节”.首先进行第一轮“选题答题环节”，答题规则是：每位同学各自从备选的5道不同题中随机抽出3道题进行答题，答对一题加10分，答错一题(不答视为答错)减5分，已知甲能答对备选5道题中的每道题的概率都是2，乙恰能答对备选5道题中的其中3道3题；第一轮答题完毕后进行第二轮“轮流坐庄答题环节”，答题规则是：先确定一人坐庄答题，若答对，继续答下一题…，直到答错，则换人(换庄)答下一题…以此类推．例如若甲首先坐庄，则他答第1题，若答对继续答第2题，如果第2题也答对，继续答第3题，直到他答错则换成乙坐庄开始答下一题，…直到乙答错再换成甲坐庄答题，依次类推两人共计答完20道题游戏结束，假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答，且记第n道题也由该同学(最先答题的同学)作答的概率为P n(1≤n≤20)，其中P1=1，已知供甲乙回答的20道题，如果某位同学有机会答第n道题且回答正确，则中，甲，乙两人答对其中每道题的概率都是13该同学加10分，答错(不答视为答错)则减5分，甲乙答题相互独立；两轮答题完毕总得分高者胜出．回答下列问题(1)请预测第二轮最先开始作答的是谁？并说明理由；(2)①求第二轮答题中P2，P3；②求证{P n−12}为等比数列，并求P n(1≤n≤20)的表达式．20.已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1，F2，离心率为12，点A在椭圆C上，|AF1|=2，∠F1AF2=60°，过F2与坐标轴不垂直的直线l与椭圆C交于P，Q两点，N为PQ的中点．(1)求椭圆C的方程;(2)设点M(0,18)，且MN⊥PQ于N，求直线MN的方程．21.已知函数f(x)=lnx+ax2+(2a+1)x．(1)讨论f(x)的单调性；(2)当a<0时，证明f(x)≤−34a−2．22. 在平面直角坐标系xOy 中，已知直线l 的参数方程为{x =12ty =√32t −1(t 为参数).在以坐标原点O 为极点，x 轴的正半轴为极轴，且与直角坐标系长度单位相同的极坐标系中，曲线C 的极坐标方程是ρ=2√2sin(π4+θ)．(1)求直线l 的普通方程与曲线C 的直角坐标方程；(2)设点P(0,−1).若直线l 与曲线C 相交于两点A ，B ，求|PA|+|PB|的值．23. 已知a ，b 都是大于零的实数．(1)证明：a 2b+b 2a≥a +b ；(2)若a >b ，证明：a 2+ab 3+1a(a−b)>4．-------- 答案与解析 --------1.答案：B解析：本题考查了集合的运算，属于基础题．首先解出A，B，再求解即可．解：集合A={x|y=√1−x}=(−∞,1]，∁R A=(1,+∞)，B={x|(x+1)(x−3)<0}=(−1,3)，则(∁R A)⋂B=(1,3)，故选B．2.答案：A解析：本题考查复数的运算和有关概念，属基础题．化简已知复数，逐项分析可得答案．解：化简可得z=2−1+i=2(−1−i) (−1+i)(−1−i)=2(−1−i)2=−1−i，∴z的虚部为−1，实部为−1，|z|=√2，z=−1+i，故选：A．3.答案：D解析：解：因为全称命题的否定是特称命题，所以命题：∀x∈R，|sinx|<1的否定是：∃x∈R，|sinx|≥1．故选：D直接利用全称命题的否定是特称命题写出结果即可．本题考查没有的否定全称命题与特称命题的否定关系，考查计算能力．4.答案：C解析：解：因为(x + y 2x)(x +y)5=(x 2+y 2)(x+y)5x；要求展开式中x 3y 3的系数即为求(x 2+y 2)(x +y)5展开式中x 4y 3的系数；展开式含x 4y 3的项为：x 2⋅C 52x 2⋅y 3+y 2⋅C 54x 4⋅y =15x 4y 3；故(x + y 2x)(x +y)5的展开式中x 3y 3的系数为15；故选：C ．先把条件整理转化为求(x 2+y 2)(x +y)5展开式中x 4y 3的系数，再结合二项式的展开式的特点即可求解．本题主要考查二项式定理的应用，二项式展开式的通项公式，二项式系数的性质，属基础题．5.答案：B解析：本题主要考查几何概型以及线性规划，属于基础题目． 求出符合条件的区域面积，比上总面积即为所求概率． 解：作出Ω中在圆C 内部的区域，如图所示，因为直线x +y =0，x −√3y =0的倾斜角分别为3π4，π6， 所以由图可得P 取自Ω的概率为3π4−π62π=724，故选B ．6.答案：C解析：本题考查了茎叶图中的极差以及众数的计算，明确各定义是关键，属于基础题．根据茎叶图计算甲的极差，找出乙成绩中出现最多的数据即可．解：由茎叶图可知，甲成绩的极差为95−78=17，乙运动员的众数，80；故选C．7.答案：D解析：根据线面垂直的性质及判定定理，线面平行性质及判定定理，逐一进行判定即可本题主要考查了空间线面位置关系的判断．要求熟练掌握线、面平行或垂直的判断条件和性质．属于中档题．解：对于A，若l//α，l⊥β，则α⊥β，正确．对于B，若α//β，m⊥α，则m⊥β，正确．对于C，若α∩β=m，l//α且l//β，则l//m，正确对于D，若α//β，m//α，则m//β或m⊂β，错误故选：D．8.答案：B解析：解：由函数，得，定义域为{x|x≠0}，故排除A，当x=1时，f(x)=0，当x>1时，f(x)>0，当0<x<1时，f(x)>0，故排除C，D，故B正确。

大庆实验中学2020届高三综合训练（二）数学试卷注意事项：1．本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，共150分，考试时间120分钟，答卷前，考生务必将自己的姓名、准考证号填写在答题卡的相应位置上．2．回答第I 卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号，写在本试卷上无效． 3．回答第II 卷时，将答案写在答题卡上，写在本试卷上无效．第I 卷（选择题 共60分)一、单选题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知{}1A x x =<，{}21xB x =<，则A B =U （ ） A ．()1,0-B ．()0,1C ．()1,-+∞D ．(),1-∞2．已知i 为虚数单位，若复数1aiz i-=+（a R ∈）的虚部为1-，则a = （ ） A ．2-B ．1C ．2D ．1-3．某运动制衣品牌为了成衣尺寸更精准，现选择15名志愿者，对其身高和臂展进行测量（单位：厘米），左图为选取的15名志愿者身高与臂展的折线图，右图为身高与臂展所对应的散点图，并求得其回归方程为1.160.5ˆ37yx =-，以下结论中不正确的为（ ）A ．15名志愿者身高的极差小于臂展的极差B ．15名志愿者身高和臂展成正相关关系，C ．可估计身高为190厘米的人臂展大约为189．65厘米D ．身高相差10厘米的两人臂展都相差11．6厘米，4．函数()2ln xf x x x=-的图象大致为 （ ）A ．B ．C ．D ．5．某几何体的三视图如图所示，则该几何体的体积为 （ ） A ．16163π-B ．32163π-C ．1683π-D ．3283π- 6．《九章算术》第三章“衰分”介绍比例分配问题，“衰分”是按比例递减分配的意思，通常称递减的比例为“衰分比”．如：已知A ，B ，C 三人分配奖金的衰分比为20%，若A 分得奖金1000元，则B ，C 所分得奖金分别为800元和640元．某科研所四位技术人员甲、乙、丙、丁攻关成功，共获得单位奖励68780元，若甲、乙、丙、丁按照一定的“衰分比”分配奖金，且甲与丙共获得奖金36200元，则“衰分比”与丁所获得的奖金分别为 ( )A ．20%，14580元B ．10%，14580元C ．20%，10800元D ．10%，10800元7．若0m >，0n >，且直线()()1120m x n y +++-=与圆222210x y x y +--+=相切，则m n +的取值范围是 （ ）A ．)22,⎡++∞⎣B ．)222,⎡++∞⎣C ．(0,22⎤+⎦ D ．(0,222⎤+⎦8．我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，用现代式子表示即为：在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，则ABC ∆的面积222221()42a b c S ab ⎡⎤⎛⎫+-⎢⎥=- ⎪⎢⎥⎝⎭⎣⎦．根据此公式，若()cos 3cos 0a B b c A ++=，且2222a b c --=，则ABC ∆的面积为（ ）A ．2B ．22C ．6D ．239．2018年9月24日，阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想，这一事件引起了数学界的震动，在1859年，德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题，也就是著名的黎曼猜想．在此之前，著名数学家欧拉也曾研究过这个问题，并得到小于数字x 的素数个数大约可以表示为()ln xn x x≈的结论（素数即质数，，则输出k 的值应属于区间 （ ） 15,20B ．20,25C ．25,30D ．30,3510．已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为()1,0F c -、()2,0F c ，且双曲线C 与圆222x y c +=在第一象限相交于点A ，且123AF AF =，则双曲线C 的离心率是（ ）A ．31+B ．21+C ．3D ．211．已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<，28f π⎛⎫=⎪⎝⎭，02f ⎛⎫= ⎪⎝⎭π且在()0,π上是单调函数，则下列说法正确的是 （ ）A ．12ω=B ．6282f π+⎛⎫-=⎪⎝⎭C ．函数()f x 在,2ππ⎡⎤--⎢⎥⎣⎦上单调递减D ．函数()f x 的图像关于点5,04π⎛⎫⎪⎝⎭对称12．定义在R 上的偶函数()f x 满足()()53f x f x -=+，且()224,012ln ,14x x x f x x x x ⎧-+≤<=⎨-≤≤⎩，若关于x 的不等式()()()210f x a f x a +++<在[]20,20-上有且仅有15个整数解，则实数a 的取值范围是（ ）A ．(]1,ln 22--B ．[)2ln 33,2ln 22--C ．(]2ln 33,2ln 22--D ．[)22ln 2,32ln 3--第II 卷（非选择题 共90分)二、填空题：本题共4小题，每小题5分，共20分．把答案填写在大题卡相应位置上．13．二项式561x x x ⎛⎫+ ⎪⎝⎭展开式中的常数项是__________．14．已知向量(1,2)a =r ，(,1)b k =r ，且2a b +r r与向量a r 的夹角为90°，则向量a r 在向量b r 方向上的投影为________．15．已知P ，E ，G F ，都在球面C 上，且P 在EFG ∆所在平面外，PE EF ⊥，PE EG ⊥，224PE GF EG ===，120EGF ∠=o ，在球C 内任取一点,则该点落在三棱锥P EFG -内的概率为__________．16．已知数列{}n a 的各项都是正数，()2*11n n n a a a n N ++-=∈．若数列{}n a 各项单调递增，则首项1a 的取值范围是________；当123a =时，记1(1)1n n nb a --=-，若1220191k b b b k <+++<+L ，则整数k =________．三、解答题：共70分．解答应写出必要的文字说明、证明过程或演算步骤．17．若ABC V 的内角A ，B ，C 的对边为a ，b ，c ，且224()si sin n sin sin sin 3A B C B C -=-. （1）求cos A ； （2）若ABC V 的面积为423，求内角A 的角平分线AD 长的最大值．18．如图，四棱锥-中，SD CD SC AB BC ====，平面⊥底面ABC ∠=︒，是中点. （1）证明：直线AE 平面 （2） A BC DSEF18．如图，四棱锥S ABCD -中，22SD CD SC AB BC ====，平面ABCD ⊥底面SDC ，//AB CD ，90ABC ∠=︒，E 是SD 中点． （1）证明：直线//AE 平面SBC ； （2）点F 为线段AS 的中点，求二面角F CD S --的大小．19．2019年春节期间，我国高速公路继续执行“节假日高速公路免费政策”．某路桥公司为掌握春节期间车辆出行的高峰情况，在某高速公路收费点记录了大年初三上午9:2010:40~这一时间段内通过的车辆数，统计发现这一时间段内共有600辆车通过该收费点，它们通过该收费点的时刻的频率分布直方图如下图所示，其中时间段9:209:40~记作区间[)20,40，9:4010:00~记作[)40,60，10:0010:20~记作[)60,80，10:2010:40~记作[]80,100，例如：10点04分,记作时刻64．（1）估计这600辆车在9:2010:40~时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表)；（2）为了对数据进行分析，现采用分层抽样的方法从这600辆车中抽取10辆，再从这10辆车中随机抽取4辆，设抽到的4辆车中,在9:2010:00~之间通过的车辆数为X ，求X 的分布列与数学期望；（3）由大数据分析可知，车辆在每天通过该收费点的时刻服从正态分布()2,N μσ，其中μ可用这600辆车在9:2010:40~之间通过该收费点的时刻的平均值近似代替，2σ可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表)，已知大年初五全天共有1000辆车通过该收费点，估计在9:46~10:22之间通过的车辆数(结果四舍五入保留到整数)．参考数据：若()2,T N μσ~,则()0.6827P T μσμσ-<≤≤=①；(22)0.9545P T μσμσ-<≤+=②；(33)0.9973P T μσμσ-<≤+=③．20．已知椭圆:C 22221(0)x y a b a b +=>>的离心率为22，焦距为2c ，直线20bx y a -+=过椭圆的C左焦点．（1）求椭圆C 的标准方程；（2）若直线20bx y c -+=与y 轴交于点,,P A B 是椭圆C 上的两个动点,APB ∠的平分线在y 轴上,PA PB ≠．试判断直线AB 是否过定点，若过定点，求出定点坐标;若不过定点，请说明理由．21．已知函数()ln f x x ax b =--． （1）求函数()f x 的极值；（2）若不等式()f x ex ≤-恒成立，求ba e-的最小值（其中e 为自然对数的底数）．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分，做答时用2B 铅笔在答题卡上把所选题目对应的题号涂黑．本题满分10分．22．选修4-4：坐标系与参数方程在平面直角坐标系xOy 中，以坐标原点O 为极点，以x 轴正半轴为极轴，建立极坐标系，曲线C 的极坐标方程为22121sin ρθ=+，射线(0)4πθρ=≥交曲线C 于点A ，倾斜角为α的直线l 过线段OA 的中点B 且与曲线C 交于P 、Q 两点．（1）求曲线C 的直角坐标方程及直线l 的参数方程；（2）当直线l 倾斜角α为何值时，BP BQ ⋅取最小值，并求出BP BQ ⋅最小值．23．选修4-5：不等式选讲已知函数() 1.f x x =+（Ⅰ）解不等式()32f x x >-+；（Ⅱ）已知0,0a b >>，且22a b +=，求证()224.f x x a b -≤+。