二端口网络参数和方程

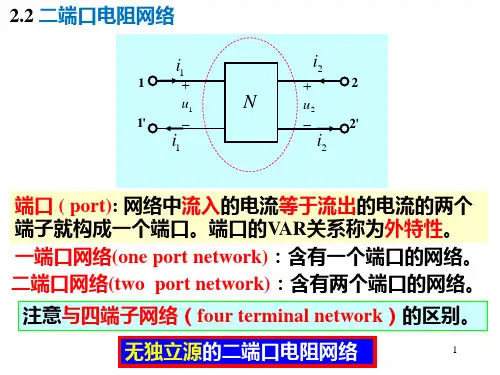
第十六章 二端口网络16.1 基本概念16.1.1 二端口网络的端口条件和端口变量1. 端口条件：在端口网络的任意端口上，由一端流入的电流必须等于由另一端流出的电流，这叫做双口网络的端口条件； 2. 端口变量：包括两个端口电压21u u ，和两个端口电流21i i ，。

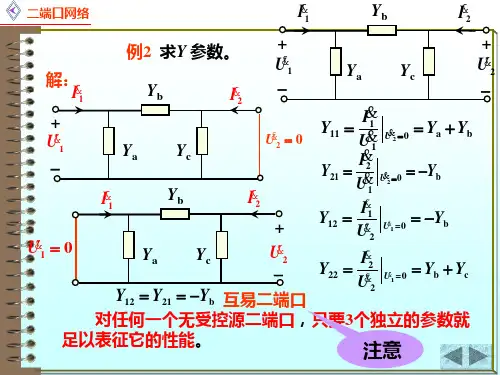
16.1.2 二端口网络的方程和参数二端口网络的对外电气性能可以用一些参数表示。

即以这些参数组成的方程对外电路表示二端口网络的电气性能。

在分析二端口的参数时，按正弦稳态情况考虑。

本章讨论的二端口是由线性电阻、电感、电容和线性受控源组成，不含任何独立电源。

如图16-1所示为一线性二端口。

11'22'116-图1. Y 参数方程用21U U ∙∙，表示21I I ∙∙，（1） 方程⎪⎩⎪⎨⎧+=+=∙∙∙∙∙∙22212122121111U Y U Y I U Y U Y I （2） 参数的物理意义。

分别把入口和出口短路出口的驱动点导纳导纳入口与出口之间的转移导纳出口与入口之间的转移入口的驱动点导纳----=----=----=----==∙∙=∙∙=∙∙=∙∙∙∙∙∙22220211201221011111122U U U U U I Y U I Y U I Y U I Y由于以上参数是在入口和出口分别短路情况下的参数，所以称为短路参数。

对于线性无源网络（指即不包含独立电源，也不包含受控源），2111Y Y =，只有三个独立参数，又称互易双口；当2211Y Y =时，称为对称双口，只有两个独立参数。

2. Z 参数方程用∙∙21I I ，表示∙∙21U U ， （1）⎪⎩⎪⎨⎧+=+=∙∙∙∙∙∙22212122121111I Z I Z U I Z I Z U （2）参数的物理意义。

分别把入口和出口开路，出口驱动点阻抗入口对出口的转移阻抗出口对入口的转移阻抗入口驱动点阻抗----=----=----=----==∙∙=∙∙=∙∙=∙∙∙∙∙∙22220211201221011111122I I I I I U Z I U Z I U Z I U Z对于互易双口，2112Z Z = ，只有三个独立参数； 对于对称双口，1211Z Z =，只有两个独立参数。

二、 二端口网络的Z 方程Z 参数...1111122...2211222U Z I Z I U Z I Z I =+=+ 其矩阵形式为：..111112..212222U Z Z I Z Z U I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦此方程称为Z 参数方程。

〔Z 〕称为开路阻抗矩阵，其元素定义为： ..121121..11220..||I I U U Z Z I I ====..212212..22110..||I I U U Z Z I I ====式中Z 11－为二端口开路时，一端口的入端阻抗；Z 22－为一端口开路时，二端口的入端阻抗；Z 12－为一端口开路时，一端口对二端口的转移阻抗； Z 21－为二端口开路时，二端口对一端口的转移阻抗。

对比上述两套方程，知：〔Z 〕＝〔Y 〕-1同理，根据互易性定理对线性无源二端口网络，Z 12＝Z 21总是成立的。

Z 参数只有3个是独立的；对于对称的二端口，则还有Z 11＝Z 22，故只有2个参数独立。

Z 与Y 之间有着互为逆阵的关系，即1-=Y Z 或 1-=Z Y⎥⎦⎤⎢⎣⎡--∆=⎥⎦⎤⎢⎣⎡11211222222112111Y Y Y Y Y Z Z Z Z 式中 2121221122211211Y Y Y Y Y Y Y Y Y -=∆而对于含有受控源的线性二端口，互易定理一般不再成立，因此21122112 , Z Z Y Y ≠≠。

【例】 求例1电路的Z 参数【解】：方法一：根据定义求（略） 方法二：根据KCL 直接列方程因为 ⎪⎪⎩⎪⎪⎨⎧-+=-+=555512222111U U U I U U U I整理得： ⎪⎪⎩⎪⎪⎨⎧+=+=2122113103535310I I U I I U所以 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3103535310Z 方法三、 已知 s Y ⎥⎦⎤⎢⎣⎡--=4.02.02.04.0 根据公式1-=Y Z 或 1-=Z YΩ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡Ω⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--∆=31035353104.02.02.04.012.01 111211222＝＝Y Y Y Y YZ【例】：求如图6-1-5所示二端口的Z 参数。

四二端口网络的H方程和H参数
（一）二端口网络H方程
在传输领域中，传输线路有着重要的意义，它是在任何数字信号处理系统中必不可少的部分。

二端口网络的H方程是用来描述网络容量参数的一种简单而强大的方法，它可以简单地描述从一个端口到另一个端口的网络行为。

H方程有助于描述非线性网络的物理行为，并且可以计算出网络的转化能力参数。

H方程的基本特征是它可以描述从一个端口到另一个端口的信号变换，也可以定义从一个端口到另一个端口的信号传输效率。

H方程有三个参数，分别是源端口（即输入端口）Hin，中继机（中间节点）Hm，和接收端口（即输出端口）Hout。

H方程可以描述处理信号的三个不同参数，它是：
Hin = 在源端口（输入端口）处的频率响应
Hm=在中继机（中间节点）处的频率响应
Hout = 在接收端口（输出端口）处的频率响应
因此，可以用H方程来描述任意网络的性能特性，它可以表示各种网络中的频率响应，以及信号的传播速度，以及信号损耗的大小。

（二）H参数
H参数是用来表示二端口网络性能参数的一组数字，它可以用来表示从一个端口到另一个端口的信号变换。

H参数包括插值，滤波器，改变特征，以及网络的频率响应等参数。

29二端口网络方程参数及等效电路
一、二端口网络方程
二端口网络的方程如下：
V1=Z11I1+Z12I2
V2=Z21I1+Z22I2
其中V1和V2代表两端口的电压，I1和I2代表两端口的电流，Z11、Z12、Z21和Z22代表四个参数，每个参数对应一条电阻等效的连续线。

二、网络方程参数
网络方程的参数：
（1）Z11：端口1的电阻或电抗，它代表端口1电流I1通过端口1
电阻时，端口1的电压。

（2）Z12：端口1和端口2的电阻或电抗，它代表端口1电流I1通
过端口1和端口2电阻时，端口2的电压。

（3）Z21：端口2的电阻或电抗，它代表端口2电流I2通过端口2
电阻时，端口1的电压。

（4）Z22：端口2和端口1的电阻或电抗，它代表端口2电流I2通
过端口2和端口1电阻时，端口2的电压。

三、网络方程等效电路
二端口网络方程可以用下图所示的等效电路来表达：
等效电路中的电压源的电压值与实际网络中可以使用的电压值相同，即V1和V2分别代表端口1和端口2的电压。

同时，Z11、Z12、Z21和
Z22分别代表端口1、端口1和端口2、端口2之间的电阻或电抗。

四、总结
二端口网络方程的形式为：V1=Z11I1+Z12I2；V2=Z21I1+Z22I2，其中V1和V2代表两端口的电压，I1和I2代表两端口的电流。

一、 二端口网络的Y 方程和Y 参数应用替代原理，将网口电压1U 和2U 用电压源代替，如图6-1-1（a ）所示。

根据叠加原理，网口电流可由分量电流叠加而得。

在图6-1-1（b ）、（c ）分量电路中，由线性网络的比例性知，1U （或2U ）单独作用产生的分量电流与1U （或2U ）成正比，且其网络常数属导纳性质，即： ⎪⎩⎪⎨⎧='='12121111U Y I U Y I⎪⎩⎪⎨⎧=''=''22222121U Y I U Y I 式中的网络常数Y 11、Y 12、Y 21、及Y 22决定于二端口网络的内部结构和元件参数。

（a ）（b ）（c ）图6-1-1由叠加原理得：⎪⎩⎪⎨⎧''+'=''+'=222111I I I I I I即22212122121111UY U Y I U Y U Y I +=+=其矩阵形式为..111112..212222Y Y U I Y Y U I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦此方程称为Y 参数方程。

〔Y 〕称为Y 参数，其元素定义为： .111.1.20|U I Y U ==.221.1.20|U I YU ==.112.2.10|U I Y U ==.222.2.10|U I YU ==式中：Y 11－为二端口短路时，一端口的入端导纳； Y 22－为一端口短路时，二端口的入端导纳；Y 12－为一端口短路时，一端口对二端口的转移导纳； Y 21－为二端口短路时，二端口对一端口的转移导纳。

【例】求图中所示 二端口网络的Y 参数,其中R 1＝5Ω，R 2＝5Ω，R 3＝5Ω。

5Ω121'2'1I ∙∙方法一：根据定义求解 （1）Y 参数方程为：22212122121111UY U Y I U Y U Y I +=+=（2）根据Y 参数的定义：.111.1.20|U I Y U ==.221.1.20|U I YU ==根据替代定理，在端口1-1’上外施电压1U ，而把端口2-2’短路，即令02=U ，如图所示：1U ∙2U ∙1∙2∙=Y 11表示端口2-2’短路时，端口1-1’处的输入导纳或驱动导纳；Y 21表示端口2-2’短路时，端口2-2’与端口1-1’之间的转移导纳。

二端口网络的H方程和H参数
H方程是一组以二端口网络的电流İ1和电压表征电压
和电流İ2的方程，即以İ1和另一端口的电压为独立变量，和另一端口电流İ2作为待求量，
方程的结构为:
上式称为二端口网络的H参数方程。

系数 H11、H12、H21、H22称为二端口网络的H参数，其中H12、H21无量纲；H11具有阻抗性质，量纲为欧姆；H22具有导纳的性质，量纲为西门子。

由于H参数的量纲不完全相同，物理量具有混合之意，故也称为混合参数方程。

H参数其矩阵形式为:
H参数可以通过二端口网络的出口短路和入口开路来分析计算或测量来确定。

H11是输出端短路时，输入端的入端阻抗。

在晶体管电路中称为晶体管的输入电阻；
H12是输入端开路时，输入与输出端的电压之比。

在晶体管电路中称为晶体管的内部电压反馈系数或反向电压传输比；
H21是输出端短路时，输出端与输入端电流之比。

在晶体管电路中称为晶体管的电流放大倍数或电流增益。

H22输入端开路时，输出端的入端导纳。

在晶体管电路中称为晶体管的输出电导。

第七章二端口网络§7-2 二端口网络的参数方程及参数一、导纳参数方程、导纳参数如图7-4所示无源线性二端口电路中，电压、电流参考方向如图所示，电路已达稳定。

假设端口电压、为已知量，、为待求量，用、表示、时，1U 2U 1I 2I 1U 2U 1I 2I 根据叠加定理，二端口网络的方程为22212122121111U Y U Y I U Y U Y I +=+=式中系数具有导纳性质，称为二端口网络的导纳参数（参数），所以上式称为导纳方程或方程。

无源二端口网络的Y 参数，仅与网络的内部结构、元件参数、工作频率有关，而与输入信号的振幅、负载的情况无关。

因此，这些参数描述了二端口网络本身的电特性。

所以导纳方程可以用矩阵形式表示为⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡2221121121Y Y Y Y I I ⎥⎥⎦⎤⎢⎢⎣⎡21U U UY I =⎥⎥⎦⎤⎢⎢⎣⎡=21I I I ⎥⎥⎦⎤⎢⎢⎣⎡=21U U U 22122111⎥⎦⎤⎢⎣⎡=Y Y Y Y Y 为端口电流列向量；为端口电压列向量；为导纳矩阵或Y 矩阵011112==U U I Y 012212==U UIY 022221==U UIY 021121==U UIY 由于每个Y 参数都是在一个端口短路情况下分析得到的，因此参数也称为短路导纳参数。

对于无源线性二端口网络可以证明，输入和输出互换位置时，不会改变由同一激励所产生的响应。

由此得出2112Y Y =即在参数中，只有三个参数是独立的，这样的网络具有互易性，称为互易网络。

如果二端口网络是对称的（即对称二端口网络），则输出端口和输入端口互换位置后，电压和电流均不改变，有2211Y Y =对互易且对称二端口网络中，则参数中只有两个参数是独立的。

【例7-1】求图7-5所示二端口网络的导纳矩阵。

解将端口2短路sj U I Y U )42(011112-=== sj U I Y U 4012212=== sj U I Y U 4021121=== sj U I Y U 3022221-=== S将端口1短路。