最新13二端口网络参数和方程汇总

三、 二端口网络的T 方程和T 参数在上述内容中我们已经介绍了Y 参数和Z 参数的求法，Y 参数和Z 参数都可用来描述一个二端口网络的端口外特性。

但在许多工程实际问题中，往往还要求知道一个端口的电流、电压与另一个端口的电流、电压之间的直接关系。

若把Y 参数方程：22212122121111U Y U Y I U Y U Y I +=+=的第二式化为2212212211I Y U Y Y U +-= 代入Y 参数方程第一式中，整理可得：221112212211121)(I Y Y U Y Y Y Y I +-= 把以上两式写成下列形式⎪⎩⎪⎨⎧-=-=221221I D U C I I B U A U式中 ⎪⎪⎩⎪⎪⎨⎧-=-=-=-=2111212211212121221Y Y D Y Y Y Y C Y B Y Y AA 、B 、C 、D 称为二端口网络的一般参数、传输参数、T 参数或A 参数。

它们的具体含义可用下式说明：0221==I U U A A 是输出端开路时，输入电压与输出电压的比值；0221=-=I I U B B 是输出端短路时，输入端对输出端的转移阻抗；0221==I U I C C 是输出端开路时，输入端对输出端的转移导纳；0221==U I I D D 是输出端短路时，输入电流与输出电流的比值。

可见，A 是一个量纲为一的量纲；B 的量纲为Ω；C 的量纲为s ；D 也是量纲为一的量。

对于无源线性二端口网络A 、B 、C 、D 只有3个是独立的，因为Y 11＝Y 22，故A ＝D 。

所以T 参数方程为：其中 ⎥⎦⎤⎢⎣⎡=D C B A T ，称为T 参数矩阵。

AD BC 可逆时，-=1AD BC A D =对称时满足:-=1,【例】 求例1中电路的T 参数【解】：方法一：根据定义求解（略）方法二：根据KCL 直接列方程求解（略）方法三：根据T 参数与Y 参数或Z 参数的转换公式(可在表6-1中查到)求⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∆---=2111212121221Y Y Y Y Y Y Y T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∆=1222212121111Z Z Z Z Z Z Z T 其中 2112221122211211Y Y Y Y Y Y Y Y Y -==∆2112221122211211Z Z Z Z Z Z Z Z Z -==∆因为已知例1的 s Y ⎥⎦⎤⎢⎣⎡--=4.02.02.04.0 12.004.016.0=-=∆Y所以 ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=26.0522.04.02.012.02.012.04.0T⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡2211D I U C B A I U【例 】：已知...1111122...2211222(1)(2)U Z I Z I U Z I Z I =+=+ ，求T 参数。

第五部分 二端口网络（一）基本概念和基本定理1、二端口网络的端口方程和参数 （1）端口特性方程在两个端口的四个变量1U 、2U 、1I 、2I 中任取两个为变量，另两个为函数构成的方程。

电压、电流方向如图示。

（2）描述二端口的四个参数矩阵Z 参数对于由线性R 、L （M ）、C 元件组成的任意二端口无源网络都有1221Z Z =,即Z 参数矩阵是对称的。

对于对称二端口有1221ZZ =、1122Z Z =Y 参数对于由线性R 、L （M ）、C 元件组成的任意二端口无源网络都有1221Y Y =,即Y 参数矩阵是对称的。

对于对称二端口有1221YY =、1122Y Y =T 参数对于由线性R 、L （M ）、C 元件组成的任意二端口无源网络都有1AD BC -=,即T 参数矩阵是对称的。

对于对称二端口有A D =.H 参数2、二端口等效电路（1）T 型电路11112Z Z Z =-212Z Z =32212Z Z Z =-(2) π型电路11112Y Y Y =+2122Y Y Y =-=- 3221Y Y Y =+ （3）如果二端口不互易，则等效T 型电路含有受控电压源，如图（4）如果二端口不互易，则等效π型电路含有受控电流源，如图3、二端口的连接（1）级联（2）并联（3）串联4、回转器和复阻抗变换器（1）回转器是一种线性非互易的多端元件。

互易定理不适应回转器。

r 和g分别称为回转电阻和回转电导，简称回转常数。

（2）负阻抗变换器电流反向型：1212,UU I kI ==，电压的大小和方向均不改变；但电流1I 经传输后变为2kI ，即改变了方向；电压反向型：1212,UkU I I =-=-,电压改变了极性(方向)，但电流方向不变；NIC 可把正阻抗变为负阻抗。

（二）典型例题及解题方法分析例题1：图示电路二端口网络是由线性电阻构成的，此对称二端口的传输参数A=2，B=30,若将电阻LR并联在22'-两端，输入端11'-的入端电阻为将电阻LR 并联在11'-两端的入端电阻的6倍，求LR解法1：由于二端口网络是由线性电阻构成的，所以有AD-BC=1，又是对称二端口，有A=D=2，C=(AD-1)/B=0.1对于上面左图 22L UR I =-122122U AU BI I CU DI =-⎧⎨=-⎩1212()()L L U AR B I I R C D I =-+⎧⇒⎨=-+⎩112300.12L L in L L U AR B R R I CR D R ++⇒===++ 对于上面右图 20I=11'20'//'20LL i n LL L AR U R A C R R A I C R R C⇒====++ 6'in in R R =3in R =Ω解法2由于二端口网络是由线性电阻构成的对称二端口，A=D=2，C=(AD-1)/B=0.1。

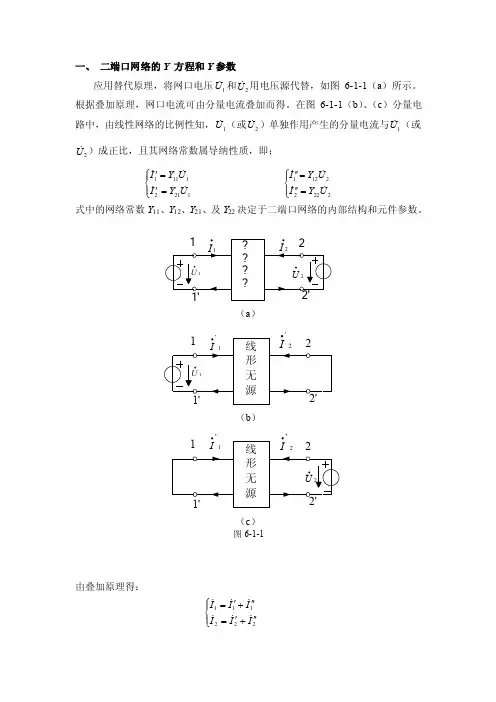
一、 二端口网络的Y 方程和Y 参数应用替代原理，将网口电压1U 和2U 用电压源代替，如图6-1-1（a ）所示。

根据叠加原理，网口电流可由分量电流叠加而得。

在图6-1-1（b ）、（c ）分量电路中，由线性网络的比例性知，1U （或2U ）单独作用产生的分量电流与1U （或2U ）成正比，且其网络常数属导纳性质，即： ⎪⎩⎪⎨⎧='='12121111U Y I U Y I⎪⎩⎪⎨⎧=''=''22222121U Y I U Y I 式中的网络常数Y 11、Y 12、Y 21、及Y 22决定于二端口网络的内部结构和元件参数。

（a ）（b ）（c ）图6-1-1由叠加原理得：⎪⎩⎪⎨⎧''+'=''+'=222111I I I I I I即22212122121111UY U Y I U Y U Y I +=+=其矩阵形式为..111112..212222Y Y U I Y Y U I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦此方程称为Y 参数方程。

〔Y 〕称为Y 参数，其元素定义为： .111.1.20|U I Y U ==.221.1.20|U I YU ==.112.2.10|U I Y U ==.222.2.10|U I YU ==式中：Y 11－为二端口短路时，一端口的入端导纳； Y 22－为一端口短路时，二端口的入端导纳；Y 12－为一端口短路时，一端口对二端口的转移导纳； Y 21－为二端口短路时，二端口对一端口的转移导纳。

【例】求图中所示 二端口网络的Y 参数,其中R 1＝5Ω，R 2＝5Ω，R 3＝5Ω。

5Ω121'2'1I ∙∙方法一：根据定义求解 （1）Y 参数方程为：22212122121111UY U Y I U Y U Y I +=+=（2）根据Y 参数的定义：.111.1.20|U I Y U ==.221.1.20|U I YU ==根据替代定理，在端口1-1’上外施电压1U ，而把端口2-2’短路，即令02=U ，如图所示：1U ∙2U ∙1∙2∙=Y 11表示端口2-2’短路时，端口1-1’处的输入导纳或驱动导纳；Y 21表示端口2-2’短路时，端口2-2’与端口1-1’之间的转移导纳。

二端口网络的Z方程和Z参数
Z方程是一组以二端口网络的电流İ1和İ2表征电压
和的方程。

二端口网络以电流İ1和İ2作为独立变量，
电压和作为待求量，根据置换定理，二端口网络端口的外部电路总是可以用电流源替代，如图1(a)所示，替代后网络是线性的，可按照叠加定理，将图1(a) 所示的网络，分解成仅含单个电流源的
网络，如图1(b)、(c)所示。

端口电压和是电流İ1、İ2
单独作用时所产生的电压之和，即
上式还可以写成如下的矩阵形式：
如果二端口网络中的电流İ2和İ1相等，所产生的开路电压和也相等时，Z12= Z21，该网络具有互易性。

如果该网络还
具有Z11= Z22的特点，则网络称为对称的二端口网络。

Z参数的确定可通过输入端口、输出端口开路测量或计算确定：
Z11是输出端开路时，输入端的入端阻抗；
Z21是输出端开路时，输出端对输入端的转移阻抗；
Z12是输入端开路时，输入端对输出端的转移阻抗；
Z22是输入端开路时，输出端的入端阻抗。