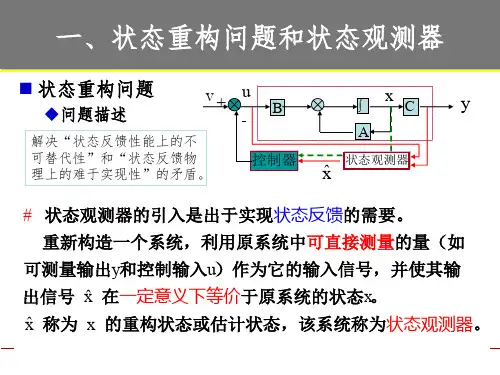
状态观测器
- 格式:ppt
- 大小:439.50 KB
- 文档页数:29


状态观测器是一种数学工具,用于估计系统状态在给定时间的状态。
它基于系统动态方程,通过测量输入和输出数据,可以推断出系统内部状态的变化。
状态观测器的原理基于卡尔曼滤波器。
卡尔曼滤波器是一种优化算法,用于通过历史数据预测未来的值,特别是对于线性系统和非线性系统的近似。
对于线性离散系统,卡尔曼滤波器能够提供最佳估计。
然而,对于非线性系统,卡尔曼滤波器的效率可能会降低。
状态观测器就是为了解决这个问题而设计的。
状态观测器的核心思想是通过设计适当的反馈控制策略,使得系统输出能够最大限度地反映系统真实状态的改变。
观测器设计依赖于对系统动态方程的理解,包括系统的输入、输出和状态变量。
通过观察系统输出,观测器可以推断出系统内部状态的变化。
在具体实现上,状态观测器通常包括两个部分:一个估计器和一个滤波器。
估计器负责估计系统的状态,而滤波器则通过测量数据(包括输入和输出)来更新这个估计。
观测器的优点在于它不需要知道系统的精确模型,只需要知道它的动态行为和某些输入输出数据。
因此,观测器可以用于各种不同的系统,包括那些具有复杂非线性特性的系统。
然而,状态观测器也有其局限性。
首先,观测器的性能受到噪声和扰动的干扰,可能会引入误差。
其次,观测器只能近似地估计系统的状态,而不能完全恢复系统的精确状态。
最后,观测器的设计需要一定的专业知识,包括对系统动态的理解和对噪声特性的认识。
总的来说,状态观测器的原理是通过设计适当的反馈控制策略和测量数据来估计系统的状态。
它基于卡尔曼滤波器,通过历史数据来预测未来的状态变化,对于线性和非线性系统的状态估计具有重要的应用价值。
然而,它也有其局限性,需要在实际应用中注意其性能和误差来源。


现代控制实验状态反馈器和状态观测器的设计现代控制实验中,状态反馈器和状态观测器是设计系统的重要组成部分。
状态反馈器通过测量系统的状态变量,并利用反馈回路将状态变量与控制输入进行耦合,以优化系统的性能指标。
状态观测器则根据系统的输出信息,估计系统的状态变量,以便实时监测系统状态。
本文将分别介绍状态反馈器和状态观测器的设计原理和方法。
一、状态反馈器的设计:状态反馈器的设计目标是通过调整反馈增益矩阵,使得系统的状态变量在给定的性能要求下,达到所需的一组期望值。
其设计步骤如下:1.系统建模:通过对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
通常表示为:ẋ=Ax+Buy=Cx+Du其中,x为系统状态向量,u为控制输入向量,y为系统输出向量,A、B、C、D为系统的状态矩阵。
2.控制器设计:根据系统的动态性能要求,选择一个适当的闭环极点位置,并计算出一个合适的增益矩阵。
常用的设计方法有极点配置法、最优控制法等。
3.状态反馈器设计:根据控制器设计得到的增益矩阵,利用反馈回路将状态变量与控制输入进行耦合。
状态反馈器的输出为:u=-Kx其中,K为状态反馈增益矩阵。
4.性能评估与调整:通过仿真或实验,评估系统的性能表现,并根据需要对状态反馈器的增益矩阵进行调整。
二、状态观测器的设计:状态观测器的设计目标是根据系统的输出信息,通过一个状态估计器,实时估计系统的状态变量。
其设计步骤如下:1.系统建模:同样地,对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
2.观测器设计:根据系统的动态性能要求,选择一个合适的观测器极点位置,以及一个合适的观测器增益矩阵。
常用的设计方法有极点配置法、最优观测器法等。
3.状态估计:根据观测器设计得到的增益矩阵,通过观测器估计系统的状态变量。
状态观测器的输出为:x^=L(y-Cx^)其中,L为观测器增益矩阵,x^为状态估计向量。
4.性能评估与调整:通过仿真或实验,评估系统的状态估计精度,并根据需要对观测器的增益矩阵进行调整。




扩张状态观测器原理
扩张状态观测器是一种用于对系统状态进行实时监测和估计的控制方法。
它的原理基于状态观测理论和系统动力学模型,通过使用系统的输入和输出数据,估计当前系统的状态。
以下是扩张状态观测器的工作原理:
1. 建立系统动力学模型:首先,需要建立系统的数学模型,描述系统的动态行为。
这通常通过差分方程或微分方程来表示系统的输入和输出之间的关系。
模型的结构和参数可以基于系统的物理原理或经验来确定。
2. 设计观测器:根据系统动力学模型,设计一个观测器来估计系统的状态。
观测器通常由一个状态估计器和一个补偿器组成。
状态估计器根据系统模型和已知的输入和输出数据,利用卡尔曼滤波、最小二乘等方法,计算出当前系统的状态估计值。
补偿器根据状态估计值和测量输出,进行补偿、校正,提高状态估计的精度。
3. 实时状态估计:在运行过程中,通过记录系统的输入和输出数据,并将其输入到观测器中。
观测器根据这些数据,实时计算出系统的状态估计值。
状态估计值可以用于系统的监测、故障检测和故障诊断等应用。
扩张状态观测器的优点是可以对系统状态进行实时估计,不需要系统的全部状态变量进行测量。
同时,它对模型误差和测量噪声有一定的鲁棒性,能够提高状态估计的准确性和稳定性。
然而,扩张状态观测器的设计需要考虑系统模型的准确性和观
测器参数的选择等因素,对观测器的稳定性和收敛性有一定的要求。
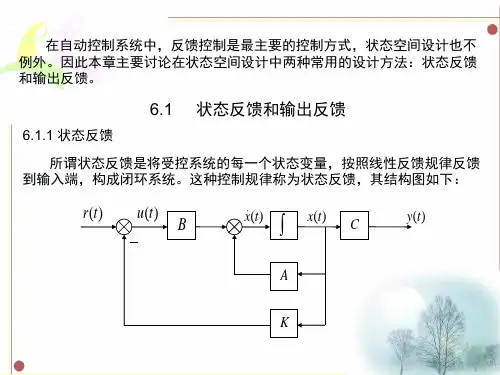

状态观测器设计利用状态反馈实现闭环系统的极点配置,需要利用系统的全部状态变量。
然而系统的状态变量并不都是能够易于用物理方法量测出来的,有些根本就无法量测;甚至一些中间变量根本就没有常规的物理意义。
此种情况下要在工程上实现状态反馈,就需要对系统的状态进行估计,即构造状态观测器。
状态观测器,是一个在物理上可以实现的动态系统,它利用待观测系统的可以量测得到的输入和输出信息来估计待观测系统的状态变量,以便用该组状态变量的估计值来代替待观测系统的真实状态变量进行状态反馈设计,实现闭环系统极点的再配置。
1. 全维状态观测器当对象的所有状态均不可直接量测时,若要进行状态反馈设计,就需对全部状态变量进行观测。
这时构造的状态观测器,其阶次与对象的阶次相同,被称为全维状态观测器。
考虑如下n阶单输出线性定常离散系统(1)其中,A为n×n维系统矩阵,B为n×r输入矩阵,C为n×1维输出矩阵。
系统结构图如图1所示。
图1 全维状态观测器构造一个与受控系统具有相同参数的动态系统(2)当系统(1)与(2)的初始状态完全一致时,则两个系统未来任意时刻的状态也应完全相同。
但在实际实现时,不可能保证二者初始状态完全相同。
为此,应引入两个系统状态误差反馈信号构成状态误差闭环系统,通过极点配置使误差系统的状态渐趋于零。
由于原受控系统状态不可直接量测,故用二个系统的输出误差信号代替。
引入了输出误差的状态观测器状态方程为(3)其中,H为状态观测器的输出误差反馈系数矩阵,有如下形式定义状态估计误差为,用式(7.65)与(7.67)相减可得(4)即(5)通过式(5)可以看出,若选择合适的输出误差反馈矩阵H 使得状态估计误差系统(5)的所有极点均位于z平面单位圆内,则误差可在有限拍内趋于零,即状态估计值在有限拍内可以跟踪上真实状态,且极点越靠近原点状态估计误差趋于零的速度越快,反之越慢。
可见,能否逼近x(k)以及逼近速度是由H阵决定的。
状态观测器摘要观测器在控制理论中非常重要。
当状态不能观测时,应设计状态观测器来估计状态。
理论分析和数值仿真证实了用所设计的观测器来估计状态的有效性。
关键字:观测器;状态观测器;设计一 全维状态观测器的设计极点配置是基于状态反馈,因此状态X 必须可观测。
当状态不能观测时,则应设计状态观测器来估计状态。
x A x B u y C x =+⎧⎨=⎩(1) 若系统完全能观测,则可构造如图1所示的状态观测器。
由上图可得观测器的状态方程为ˆˆˆxA xB u LC x L y =+-+ (2) 即 ˆˆ x (A L C )x B u L y =-++ 其特征多项式为()()f s sI A L C =--由于工程上要求ˆ x能比较快速的逼近 x ,只要调整反 馈矩阵 L, 观测器的极点就可以 任意配置达到要求的性能。
假定单变量所要求的 n 个 观测器的极点为:123.................n λλλλ , 则可求出期望的状态观测器的特征方程为:112()( n n nn n f s s a s a λλλλλλ-=---=++这时可求得反馈矩阵 L 为:10()...1o o L f A V -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ (3) 式中1...o n C C A V C A -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是将系统期望的观测器特征方程中 S 换成系统矩阵 A后的矩阵多项式。
利用对偶原则, 可使设计问题大为简化, 求解过程如下:( 1)构造系统式( 1)的对偶系统T TT z A z C B z ηω⎧=+⎪⎨=⎪⎩ (4) ( 2)用MATLAB 的函数 p l ace ( )及 acker ( ), 根据下式可求得状态观测器的反馈矩阵Lk e r(,,)T T T L a c A C P =或(,,)T T TL p la c e A C P = (5) 其中, P 为给定的极点, L 为状态观测器的反馈矩阵。
离散控制系统中的状态观测器设计离散控制系统是指系统的输入和输出是离散的,并且在时间上以离散的方式进行测量和控制。
状态观测器是离散控制系统中重要的组成部分,用于估计系统的状态变量,从而实现对系统的控制。
本文将介绍离散控制系统中状态观测器的设计方法及其应用。
一、状态观测器的概念和作用状态观测器是一种用于估计系统状态的装置或算法。
在离散控制系统中,通过观测系统的输出值和输入值,结合系统的数学模型,状态观测器能够推断出系统的状态变量,从而实现对系统的监测和控制。
状态观测器在离散控制系统中具有重要的作用。
首先,通过对系统状态的估计,可以实现对系统的运行状态的实时监测,减少故障的发生。
其次,状态观测器可以提供系统未知状态变量的估计值,从而实现对系统的控制。
因此,状态观测器在离散控制系统中具有广泛的应用。
二、状态观测器的设计方法状态观测器的设计方法可以分为两类:基于传统观测器设计方法和基于最优观测器设计方法。
1. 基于传统观测器设计方法基于传统观测器设计方法的核心思想是通过系统的输出值来估计系统的状态变量。
最常用的传统观测器设计方法有:(1)全阶观测器设计:全阶观测器是指观测器的状态向量与系统的状态向量具有相同的维数。
全阶观测器可以通过系统的输出值和输入值来准确地估计系统的状态变量。
(2)低阶观测器设计:低阶观测器是指观测器的状态向量比系统的状态向量的维数低。
低阶观测器设计方法通过将系统的状态变量投影到一个低维的观测空间中来实现对系统状态的估计。
2. 基于最优观测器设计方法基于最优观测器设计方法的核心思想是通过优化问题来设计状态观测器,使得估计误差最小。
最优观测器能够最大程度地准确估计系统的状态变量。
最常用的最优观测器设计方法是卡尔曼滤波器。
卡尔曼滤波器能够通过系统的输出值和输入值来估计系统的状态变量,并且可以自适应地调整观测器的参数,以最小化估计误差。
三、状态观测器的应用状态观测器在离散控制系统中有广泛的应用。