下载文档原格式
一、填空题1、机械振动按不同情况进行分类大致可分成（线性振动）和非线性振动；确定性振动和（随机振动）；（自由振动）和强迫振动。
2、周期运动的最简单形式是（简谐运动），它是时间的单一（正弦）或（余弦）函数。
3、单自由度系统无阻尼自由振动的频率只与（质量）和（刚度）有关，与系统受到的激励无关。
4、简谐激励下单自由度系统的响应由（瞬态响应）和（稳态响应）组成。
5、工程上分析随机振动用（数学统计）方法，描述随机过程的最基本的数字特征包括均值、方差、（自相关函数）和（互相关函数）。
6、单位脉冲力激励下，系统的脉冲响应函数和系统的（频响函数）函数是一对傅里叶变换对，和系统的（传递函数）函数是一对拉普拉斯变换对。
2、在离散系统中，弹性元件储存( 势能 )，惯性元件储存（动能 ），（阻尼 ）元件耗散能量。
4、叠加原理是分析（线性 ）系统的基础。
5、系统固有频率主要与系统的（刚度 ）和（质量 ）有关，与系统受到的激励无关。
6、系统的脉冲响应函数和（频响函数 ）函数是一对傅里叶变换对，和（传递函数 ）函数是一对拉普拉斯变换对。
7、机械振动是指机械或结构在平衡位置附近的（往复弹性 ）运动。
1．振动基本研究课题中的系统识别是指 根据已知的激励和响应特性分析系统的性质，并可得到振动系统的全部参数。
（本小题2分）2．振动按激励情况可分为 自由振动 和 强迫振动 两类。
（本小题2分）。
3．图（a ）所示n 个弹簧串联的等效刚度=k ∑=ni ik111；图（b ）所示n 个粘性阻尼串联的等效粘性阻尼系数=e C ∑=ni ic 111。
（本小题3分）（a ） （b ）题一 3 题图4．已知简谐振动的物体通过距离静平衡位置为cm x 51=和cm x 102=时的速度分别为s cm x 201= 和s cm x 82= ，则其振动周期=T 2.97s ；振幅=A 10.69cm 。
（本小题4分）5．如图（a ）所示扭转振动系统，等效为如图（b ）所示以转角2ϕ描述系统运动的单自由度系统后，则系统的等效转动惯量=eq I 221I i I +，等效扭转刚度=teq k 221t t k i k +。
25第2章 单自由度系统的自由振动2.1 无阻尼系统的自由振动设有质量为m 的物块(可视为质点)挂在弹簧的下端，弹簧的自然长度为l 0,弹簧刚度为k ，如不计弹簧的质量，这就构成典型的单自由度系统，称之为弹簧质量系统如图2-1所示。
工程中许多振动问题都可简化成这种力学模型。
例如，梁上固定一台电动机，当电机沿铅直方向振动时，梁和电机组成一个振动系统，如不计梁的质量，则它在该系统中的作用相当于一根无重弹簧，而电机可视为集中质量。
于是这个系统可简化成如图2-1所示的弹簧质量系统。
2.1.1自由振动方程以图2-1所示的弹簧质量系统为研究对象。
取物块的静平衡位置为坐标原点O ，x 轴顺弹簧变形方向铅直向下为正。
当物块在静平衡位置时，由平衡条件∑F x = 0，得到st δk mg = （A ）st δ称为弹簧的静变形。
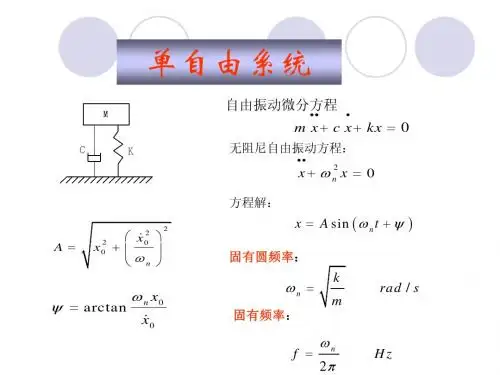
当物块偏离平衡位置为x 距离时，物块的运动微分方程为mxkx &&=− （2-1） 将式（2-1）两边除以m ，并令mkp =n （2-2） 则式（2-1）可写成02n =+x p x && （2-3）这就是弹簧质量系统置之只在线弹性力－kx 的作用下所具有的振动微分方程，称之为无阻尼自由振动的微分方程，是二阶常系数线性齐次方程。
由微分方程理论可知，式（2-3）的通解为t p C t p C x n 2n 1sin cos +=其中C 1和C 2为积分常数，由物块运动的起始条件确定。
设0=t 时，x x xx ==00，&&。
可解得 C x 10= n02p xC &=t p p xt p x x n n0n 0sin cos &+= （2-4） 式（2-4）亦可写成下述形式)sin(n α+=t p A x （2-5）26 其中⎪⎪⎩⎪⎪⎨⎧=+=)arctan()(00n 2n020x x p p x x A &&α （2-6） 式（2-4）、（2-5）是物块振动方程的两种形式，称为无阻尼自由振动，简称自由振动。
胡海岩主编---机械振动基础课后习题解答_第2章习题第2章习题含答案习题2-1 定常力作用下的单自由度系统1. 一个单自由度系统的质量m=2kg，刚度k=1000N/m，阻尼系数c=10N·s/m。
试求该系统的固有频率、阻尼比和振动的稳定性。
解：根据公式，该系统的固有频率可计算为：ωn = √(k/m) = √(1000/2) ≈ 22.36 rad/s阻尼比可计算为：ξ = c/(2√(mk)) = 10/(2√(2×1000)) ≈ 0.158振动的稳定性取决于阻尼比ξ的大小。
当ξ<1时，系统为欠阻尼；当ξ=1时，系统为临界阻尼；当ξ>1时，系统为过阻尼。
2. 一个单自由度系统的质量m=5kg，刚度k=500N/m，阻尼系数c=20N·s/m。
试求该系统的固有频率、阻尼比和振动的稳定性。
解：根据公式，该系统的固有频率可计算为：ωn = √(k/m) = √(500/5) = 10 rad/s阻尼比可计算为：ξ = c/(2√(mk)) = 20/(2√(5×500)) ≈ 0.141振动的稳定性取决于阻尼比ξ的大小。
当ξ<1时，系统为欠阻尼；当ξ=1时，系统为临界阻尼；当ξ>1时，系统为过阻尼。
习题2-2 强迫振动的幅值和相位1. 一个单自由度系统的质量m=3kg，刚度k=2000N/m，阻尼系数c=30N·s/m。
给定的外力F(t) = 10sin(5t)N。
试求该系统在稳态时的振动幅值和相位。
解：首先求解系统的强迫响应，即对外力F(t)进行拉氏变换：F(s) = L{F(t)} = L{10sin(5t)} = 10L{sin(5t)} = 10×(5/(s^2+25))根据公式，系统的强迫响应可计算为：X(s) = F(s)/((s^2+ωn^2)+2ξωns)其中，ωn=√(k/m)为系统的固有频率，ξ=c/(2√(mk))为系统的阻尼比。
