单自由度系统的振动

第二章单自由度系统振动§1-1 概述单自由度系统的振动理论是振动理论的理论基础。

(1)尽管实际的机械都是弹性体或多自由度系统，然而要掌握多自由度振动的基本规律，就必须先掌握单自由度系统的振动理论。

此外，(2)许多工程技术上的具体振动系统在一定条件下，也可以简化为单自由度振动系统来研究。

[举例如下：]例如：(1)悬臂锤削镗杆；(2)外圆磨床的砂轮主轴；(3)安装在地上的床身等。

[力学模型的简化方法]若忽略这些零部件中的镗杆、主轴和转轴的质量，只考虑它们的弹性。

忽略那些支承在弹性元件上的镗刀头、砂轮、床身等惯性元件的弹性，只考虑它们的惯性。

把它们看成是只有惯性而无弹性的集中质点。

于是，实际的机械系统近似地简化为单自由度线性振动系统的动力学模型。

在实际的振动系统中必然存在着各种阻尼，故模型中用一个阻尼器来表示。

阻尼器由一个油缸和活塞、油液组成。

汽车轮悬置系统等等。

[以上为工程实际中的振动系统]单自由度振动系统——指用一个独立参量便可确定系统位置的振动系统。

所有的单自由度振动系统经过简化，都可以抽象成单振子，即将系统中全部起作用的质量都认为集中到质点上，这个质点的质量m 称为当量质量，所有的弹性都集中到弹簧中，这个弹簧刚度k称为当量弹簧刚度。

以后讨论中，质量就是指当量质量，刚度就是指当量弹簧刚度。

在单自由度振动系统中，质量m、弹簧刚度k、阻尼系数C是振动系统的三个基本要素。

有时在振动系统中还作用有一个持续作用的激振力P。

应用牛顿运动定律，作用于一个质点上所有力的合力等于该质点的质量和该合力方向的加速度的乘积。

（牛顿运动定律）（达伦培尔原理）现取所有与坐标x 方向一致的力、速度和加速度为正，则：kx x C t P xm --= ωsin 0 (牛顿运动定律) （达伦培尔原理：在一个振动体上的所有各力的合力必等于零） （动静法分析：作用在振动体上的外力与设想加在此振动体上的惯性力组成平衡力系）上式经整理得，t P kx x C xm ωsin 0=++ （2.1） 该式就是单自由度线性振动系统的运动微分方程式的普遍式。

y sy(t)机械振动分析------单自由度无阻尼系统的自由振动机械振动是物体(或物体的一部分)在平衡位置（物体静止时的位置）附近作的往复运动。

可分为自由振动、受迫振动。

又可分为无阻尼振动与阻尼振动。

常见的简谐运动有弹簧振子模型、单摆模型等。

振动在机械中的应用非常普遍,例如在振动筛分行业中基本原理系借电机轴上下端所安装的重锤（不平衡重锤），将电机的旋转运动转变为水平、垂直、倾斜的三次元运动，再把这个运动传达给筛面。

若改变上下部的重锤的相位角可改变原料的行进方向。

物体受到初干扰后，仅在系统的恢复力作用下在其平衡位置附近的振动称为无阻尼自由振动。

其中仅需用一个独立坐标就可确定振体位置的系统为单自由度系统。

单自由度系统的振动理论是振动理论的基础。

研究单自由度系统的振动有着非常普遍的实际意义，因为工程上有许多问题通过简化，用单自由度系统的振动理论就能得到满意的结果。

而同时对多自由度系统和连续系统的振动，在特殊坐标系中考察时，显示出与单自由度系统类似的性态。

因此，揭示单自由度振动系统的规律、特点，为进一步研究复杂振动系统奠定了基础。

影响振动作用的因素是振动频率、加速度和振幅。

现在我们就此方面展开对单自由度无阻尼振动的讨论。

主要包括两部分：单自由度无阻尼系统的自由振动和单自由度无阻尼系统的受迫振动。

一、单自由度无阻尼系统的自由振动如下图，设此梁上的集中质量为m ，其重量为W mg ，梁由于质量的重力引起的质量处的静力位移用s y 表示，与s y 相应的质量位置称为质量的静力平衡位置。

若此质量受到扰动离开了静力平衡位置，当扰动除去后，则体系将发生振动，这样的振动称为体系的自由振动。

由于振动的方向与梁轴垂直，故称为横向振动。

在此，只讨论微小振幅的振动，由振动引起的内力限于材料的弹性极限以内，用以表示质量运动的方程将为线性微分方程。

1、建立运动方程建立运动方程常用的基本原理是达朗伯原理（亦称惯性力法或动静法）。

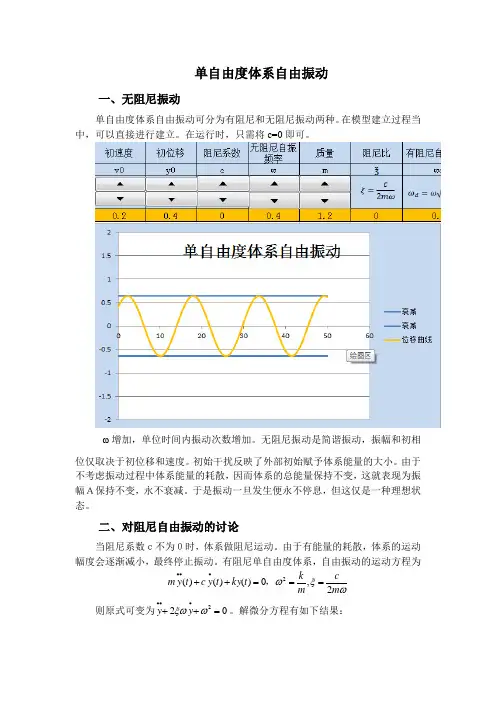
单自由度体系自由振动一、无阻尼振动单自由度体系自由振动可分为有阻尼和无阻尼振动两种。

在模型建立过程当中，可以直接进行建立。

在运行时，只需将c=0即可。

ω增加，单位时间内振动次数增加。

无阻尼振动是简谐振动，振幅和初相位仅取决于初位移和速度。

初始干扰反映了外部初始赋予体系能量的大小。

由于不考虑振动过程中体系能量的耗散，因而体系的总能量保持不变，这就表现为振幅Ａ保持不变，永不衰减。

于是振动一旦发生便永不停息，但这仅是一种理想状态。

二、对阻尼自由振动的讨论当阻尼系数ｃ不为０时，体系做阻尼运动。

由于有能量的耗散，体系的运动幅度会逐渐减小，最终停止振动。

有阻尼单自由度体系，自由振动的运动方程为ωξωm c m k t ky t y c t y m 2,0)()()(2===++∙∙∙， 则原式可变为022=++∙∙∙ωξωy y 。

解微分方程有如下结果：2.1 当1<ξ时，即小阻尼运动，方程的解为：)sin(A )sin cos ()(000ϕωωωξωωξωξω+=++=--t e t y v t y e t y d t d d d t 其中2200201)(ξωωωξω-=++=d d y v y A可画出小阻尼体系自由振动时的ｙ－ｔ曲线如图所示：是一条逐渐衰减的波动曲线2.2 当1>ξ时，即大阻尼的情况，方程的解为：⎥⎥⎦⎤⎢⎢⎣⎡-+--+=-t ch y t sh v y e t y o t ωξωξξξωωξ11)1()(20220 上式不含有简谐振动的因子，是因为体系受干扰后偏离平衡位置所积蓄起来的初始能量在恢复平衡位置的过程中全部消耗克服阻尼，由于阻尼很大，不足以引起振动。

当初始速度，初始位移都大于０时，可画出大阻尼体系自由振动时的ｙ－ｔ曲线如图所示：2.3 当1=ξ时，即临界阻尼的情况，方程的解为：[]t v t y e t y t 00)1)(++=-ωω（当初始速度，初始位移都大于０时，可画出临界阻尼体系自由振动时的ｙ－ｔ曲线如下图所示；当体系在临界阻尼时，其运动衰减的最快，即他能在最短时间内无振动的回到平衡位置。

25第2章 单自由度系统的自由振动2.1 无阻尼系统的自由振动设有质量为m 的物块(可视为质点)挂在弹簧的下端，弹簧的自然长度为l 0,弹簧刚度为k ，如不计弹簧的质量，这就构成典型的单自由度系统，称之为弹簧质量系统如图2-1所示。

工程中许多振动问题都可简化成这种力学模型。

例如，梁上固定一台电动机，当电机沿铅直方向振动时，梁和电机组成一个振动系统，如不计梁的质量，则它在该系统中的作用相当于一根无重弹簧，而电机可视为集中质量。

于是这个系统可简化成如图2-1所示的弹簧质量系统。

2.1.1自由振动方程以图2-1所示的弹簧质量系统为研究对象。

取物块的静平衡位置为坐标原点O ，x 轴顺弹簧变形方向铅直向下为正。

当物块在静平衡位置时，由平衡条件∑F x = 0，得到st δk mg = （A ）st δ称为弹簧的静变形。

当物块偏离平衡位置为x 距离时，物块的运动微分方程为mxkx &&=− （2-1） 将式（2-1）两边除以m ，并令mkp =n （2-2） 则式（2-1）可写成02n =+x p x && （2-3）这就是弹簧质量系统置之只在线弹性力－kx 的作用下所具有的振动微分方程，称之为无阻尼自由振动的微分方程，是二阶常系数线性齐次方程。

由微分方程理论可知，式（2-3）的通解为t p C t p C x n 2n 1sin cos +=其中C 1和C 2为积分常数，由物块运动的起始条件确定。

设0=t 时，x x xx ==00，&&。

可解得 C x 10= n02p xC &=t p p xt p x x n n0n 0sin cos &+= （2-4） 式（2-4）亦可写成下述形式)sin(n α+=t p A x （2-5）26 其中⎪⎪⎩⎪⎪⎨⎧=+=)arctan()(00n 2n020x x p p x x A &&α （2-6） 式（2-4）、（2-5）是物块振动方程的两种形式，称为无阻尼自由振动，简称自由振动。

第2章 单自由度(SDOF)系统振动(Single Degree of freedom)如果振动系统任意时刻的空间位置只需要一个独立参数来表达，则称为单自由度系统。

本章介绍单自由度系统运动方程的建立，以及自由振动的特点和动力响应的计算问题。

2.1 运动方程的建立此处分别应用基于达朗贝尔原理的直接平衡法、虚位移原理和哈密顿原理建立振动微分方程。

2.1.1 直接平衡法承受动力荷载作用的任何单自由度系统均可以由图2—1所示的模型来代表。

图2—1(a)中，m 为质量块的质量(kg )，是为弹簧的刚度(m N /)，c 为粘滞阻尼系数(m s N /⋅)，)(t P 为干扰力(N )。

将坐标原点设在质量块的静平衡位置处，坐标y 即为相对于静平衡位置产生的质量块的动位移。

在任意瞬时取质量块的隔离体，如图2—1(b)所示，作用于质量块上的力有下列四种：（1）弹性恢复力（它等于弹簧刚度k 与位移y 的乘积），ky f s =，与位移的方向相反；（2）阻尼力（假设为粘滞阻尼机理，它等于阻尼常数c 与速度y 的乘积），yc f D =，与速度的方向相反；（3）惯性力（根据d ’Alembert 原理，它等于质量m 与加速度y的乘积），ym f I =，与加速度的方向相反； （4）干扰力，)(t P .（根据竖向力的动平衡条件即直接平衡法得出）)(t P ky y c ym =++ (2—1) 在振动的任意时刻，这四种力都保持着平衡，只是各个力所占的比例不同而已。

由方程(2—1)可知，相对于动力系统的静力平衡位置所建立的运动方程是不受重力影响的。

换言之，此类情况可以不考虑重力影响建立方程。

由于这个原因，建立方程时，位移都以静力平衡位置作为坐标原点，由此方程仅能得到系统的动位移，而总的位移应该是动力位移响应和静力位移值的叠加。

2.1.2 虚位移原理以图2—1所示的结构系统说明如何应用虚位移原理建立方程。

令质量m 发生虚位移y δ，则作用在质量m 上的四个力所作的总虚功应该等于零，即0)(=+---y t P y f y f y f s D I δδδδ式中的负号是因为力的方向和虚位移的方向相反。