拉普拉斯变换的定义、收敛域

积分性质
积分性质
若 $f(t)$ 的拉普拉斯变换为 $F(s)$， 则 $int_{0}^{infty} f(t) dt$ 的拉普拉 斯变换为 $- frac{1}{s} F(s)$。
应用
积分性质在求解初值问题和极值问题 时非常有用，可以方便地得到原函数 的表达式。
微分性质
微分性质
若 $f(t)$ 的拉普拉斯变换为 $F(s)$，则 $f^{(n)}(t)$ 的拉普拉斯变换为 $s^{n} F(s) - s^{n-1} f(0-) - s^{n-2} f'(0-) - ldots - f^{(n-1)}(0-)$。
卷积定理
总结词
卷积定理是拉普拉斯变换的一个重要特性， 它描述了函数与其导数之间的卷积关系。
详细描述
卷积定理表明，对于任意实数t，如果函数 f(t)与其导数f'(t)的拉普拉斯变换都存在，则 它们之间的卷积结果等于零。这个定理在信 号处理、控制系统等领域有着广泛的应用， 可以帮助我们更好地理解和分析函数的性质
，再通过反变换得到 (y(t))。
控制系统的稳定性分析
总结词
通过拉普拉斯变换，可以分析控制系统的稳定性，为系 统设计和优化提供依据。
详细描述
对于线性时不变控制系统，通过拉普拉斯变换，可以将 其转化为传递函数的形式。根据传递函数的极点和零点 分布，可以判断系统的稳定性。如果所有极点都在复平 面的左半部分，则系统是稳定的。如果极点在右半部分 或等于零，则系统是不稳定的。此外，系统的动态性能 也可以通过传递函数的极点和零点分布进行分析和优化 。
03
动态行为。
2023
PART 02
拉普拉斯变换的应用
REPORTING
在微分方程中的应用

拉普拉斯变换定义式：设有一时间函数f(t) [0,∞] 或 0≤t≤∞单边函数 ,其中，S=σ+jω是复参变量，称为复频率。

左端的定积分称为拉普拉斯积分，又称为f(t)的拉普拉斯变换；右端的F(S)是拉普拉斯积分的结果，此积分把时域中的单边函数f(t)变换为以复频率S为自变量的复频域函数F(S)，称为f(t)的拉普拉斯象函数。

以上的拉普拉斯变换是对单边函数的拉普拉斯变换，称为单边拉普拉斯变换。

如f(t)是定义在整个时间轴上的函数，可将其乘以单位阶跃函数，即变为f(t)ε（t），则拉普拉斯变换为F(s),=mathcal left =int_ ^infty f(t),e^ ,dt 其中积分下标取0-而不是0或0+ ，是为了将冲激函数δ(t)及其导函数纳入拉普拉斯变换的范围。

z变换可将分散的信号（现在主要用于数字信号）从时域转换到频域。

作用和拉普拉斯变换（将连续的信号从时域转换到频域）是一样的。

拉普拉斯变换是将时域信号变换到“复频域”，与傅里叶变换的“频域”有所区别。

FT[f(t)]=从负无穷到正无穷对[f(t)exp(-jwt)]积分 ,LT[f(t)]=从零到正无穷对[f(t)exp(-st)]积分 ,(由于实际应用，通常只做单边拉普拉斯变换，即积分从零开始) .具体地，在傅里叶积分变换中，所乘因子为exp(-jwt)，此处，-jwt显然是为一纯虚数；而在拉普拉斯变换中，所乘因子为exp(-st)，其中s为一复数：s=D+jw,jw是为虚部，相当于Fourier变换中的jwt，而D则是实部，作为衰减因子，这样就能将许多无法作Fourier变换的函数（比如exp(at),a>0）做域变换。

拉普拉斯变换主要用于电路分析，作为解微分方程的强有力工具（将微积分运算转化为乘除运算）。

但随着CAD的兴起，这一作用已不怎么受重视了，但关于其收敛域的分析（零极点图）依然常用。

Fourier 变换则随着FFT算法（快速傅立叶变换）的发展已经成为最重要的数学工具应用于数字信号处理领域。

∫
∞
s
a s s π ds = arctan = − arctan 2 2 s +a as 2 a
21
四、延时（时域平移） 延时（时域平移）
若LT [ f (t )] = F ( s ), 则当t0 > 0时, 有 : LT [ f (t − t0 )u (t − t0 )] = e
− st0
F ( s)
1 (18) (1 − e − at ) t
−3t
∫ ∫
∞
s
1 1 s ( − )ds = ln s s+a s+a
∞
s
s = − ln s+a
∞
(19)
e
−e t
−5t
∞
s
1 1 s+3 s+5 ( − )ds = ln = ln s+3 s+5 s+5 s s+3
∞
sin( at) ( 20) t
11
例4 − 1 求f (t ) = sin( ωt )的拉氏变换F ( s).
1 jωt − jω t f (t ) = sin(ωt ) = (e − e ) 2j
e j ω t − e − jω t F ( s ) = LT [sin(ωt )] = LT [ ] 2j 1 1 1 1 jω t − jω t = − ( LT [e ] − LT [e ]) = [ ] 2j 2 j s − jω s + j ω
18
三、时域积分与复频域积分特性 1、时域积分特性
若LT [ f (t )] = F ( s ), 则LT [ ∫ 其中 : f
( −1) t −∞

拉普拉斯变换收敛域与极点
拉普拉斯变换的收敛域是指使得变换积分存在的复平面上的区域。

在收敛域内，拉普拉斯变换是收敛的，也就是说变换存在。

拉普拉斯变换的极点是指函数在复平面上的奇异点，即使拉普拉斯变换在某一点处无穷大或不收敛。

极点可以是有限个或无穷个，也可能是虚轴上的点。

极点的位置对于收敛域以及函数在时域和频域的性质有重要影响。

一般而言，拉普拉斯变换的收敛域是由极点和性质受限制的，不同的极点位置可能导致不同的收敛域。

比如当极点全部在左半平面内时，拉普拉斯变换的收敛域是右半平面，即实部大于某一值的区域。

当极点在右半平面内时，拉普拉斯变换的收敛域是左半平面，即实部小于某一值的区域。

如果极点在虚轴上，则收敛域为左半平面和虚轴上除了极点处的点之外的区域。

总之，拉普拉斯变换的收敛域与极点的位置密切相关，极点的位置可以决定拉普拉斯变换的收敛性和性质。

− − −
ω
p2 + ω2
1 (3)由于 2 ⇔ sin ωt , ⇔ e −( R L ) t p + ω2 p+R L 引用卷积定理完成反演， E0 t −( R L )( t −τ ) E0 −( R L ) t ( R L )τ ( R L) sin ωt − ω cos ωt t j (t ) = sin ωτdτ = {e [e ] |0 } 2 2 2 ∫0 e L L R L +ω E0 ( R L) sin ωt − ω cos ωt E0 ωe −( R L ) t = + 2 2 2 L R L +ω L R 2 L2 + ω 2
wuxia@
至于它在初始时刻之前的值，不关心，不妨 设f(t)=0 (t<0)。 为了获得宽松的变换条件，把f(t)加工为 g(t)=e-σt f(t). e-σt 是收敛因子，即，正实数σ 的值选的足够大，以保证g(t)在(-∞,∞)上绝 对可积。 于是，可以对g(t)做傅里叶变换，
− 3 2
wuxia@
−
（二）查表法
e −τp 例2：求 解： 1 1 查表得 , ⇔ πt p e −τp 1 再利用延迟定理 ⇔ p π (τ − t ) p 的原函数.
wuxia@
ω p+λ 例3：求 和 的原函数。 2 2 2 2 ( p + λ) + ω ( p + λ) + ω
t0 ∞ − p ( ξ + t0 )
dξ = e
− pt0
∫
∞
t0
f (ξ )e
− pξ
dξ = e
− pt0
−
f ( p)

sT
(1e 2
)
25
f(t) F(s)11 esTs2E ((22 T T))2(1esT 2)
1 1esT
2
E(2T) s2 (2T)2
26
3.比例性（尺度变换）
设 f(t) F (s),则 f(a t) 1F (s),a 0 aa
例 已知L[f(t)]=F(s)，试求
L [ f ( a t 0 t )( a t 0 t )a ] 0 ( ,t 0 0 )
7
收敛域 lt i m f(t)et0(0)
• 有始有终信号和能量 整个平面
j
有限信号
•等幅0振荡0信或号和0 增a长信 以 0 为界
号
j
0 a
• 不收敛信号 et2, t et2 (0t)
除非 (0tT) 8
双边拉氏变换收敛域— f (t)u(t)etu(t)
f(t)e td t u (t)e td t0u ( t)e ( 1 )td
s 0
0 s0
F (s) s
33
若积分下限由 开始
t
0
t
f()d f()d f()d
0
f1(0) t f()d 0
4 ) f( t t 0 )( t t 0 ) s i n 0 ( t t 0 )( t t 0 )
L [ s in0 ( t t0 )( t t0 ) ] e s t0 L [ s in0 t] e s t0s 2 00 2
22
例 求锯齿波的拉氏变换
f (t) E
Tt
解：
fa (t)
证明:由定义
L[d(ft)] d(ft)estdt
dt
0 dt
estf(t)(s)estf(t)dt 0 0

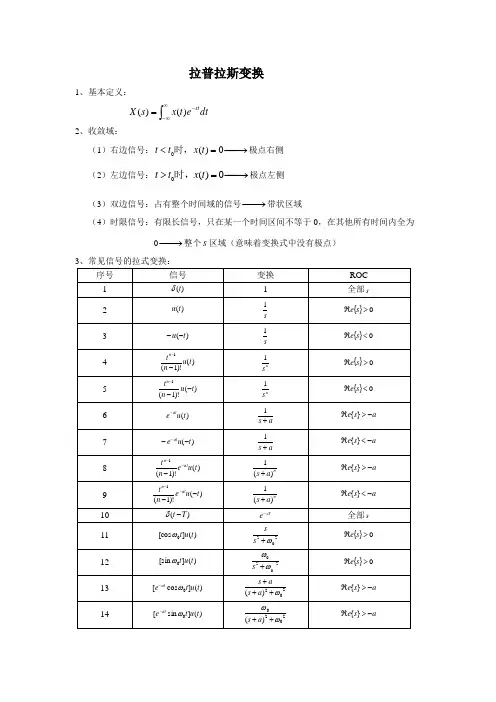
拉普拉斯变换 1、基本定义： ⎰∞∞--=dt e t x s X st )()(2、收敛域：（1）右边信号：−→−=<0)(0t x t t 时，极点右侧 （2）左边信号：−→−=>0)(0t x t t 时，极点左侧（3）双边信号：占有整个时间域的信号−→−带状区域 （4）时限信号：有限长信号，只在某一个时间区间不等于0，在其他所有时间内全为0−→−整个s 区域（意味着变换式中没有极点）4、拉式变换的主要性质：)()()()()()(11s X t x s X t x s X t x LLL−→←−→←−→← ROC: 21R R R5、用拉普拉斯变换分析与表征LTI 系统一个LTI 系统输入和输出的拉普拉斯变换是通过乘以系统单位冲激响应的拉普拉斯变换联系起来的，即)()()(s X s H s Y =当ωj s =时，)(s H 就是这个LTI 系统的频率响应；在拉普拉斯变换范畴内，一般称)(s H 为系统函数或转移函数（1）因果性（2）稳定性6、由线性常系数微分方程表征的LTI 系统 见504P7、系统函数的代数属性与方框图表示两系统级联：单位冲激响应 )()()(21t h t h t h *=→)()()(21s H s H s H=两系统并联：单位冲激响应 )()()()()()(2121s H s H s H t h t h t h +=→+=两LTI 系统的反馈互联：)()(1)()()()(211s H s H s H s H s X s Y +==−→−+)(t x )(t y8、单边拉式变换：重要价值在于求解非零状态下的系统响应⎪⎩⎪⎨⎧==⎰⎰+-∞-ωσωσπj j st st ds e s X t x dte t x s X )(21)()()(0 收敛域：要么在极点的右半平面，要么是整个s 平面（1）单边拉普拉斯变换性质（2）利用单边拉普拉斯变换求解微分方程 见518P。

t
Re(s) 0
4)卷积特性（convolution）
若 则有
f1 (t) L F1 (s) f 2 (t) L F2 (s)
Re( s) s 1 Re( s) s 2
f1 (t) f 2 (t) L F1 (s)F2 (s) Re( s) max( s 1,s 2 )
L[ f1(t) f2 (t)] 0
F
(
s)
1 s2
e - s 1
Re(s) -
例：单边周期信号的Laplace变换。 f(t)
单边周期信号的定义：
f(t)=f(t+nT); t0, n=0,1,2,...
0 T 2T 3T
t
定义：f1
(t)
f 0
(t
)
0t T 其它
单边周期信号
f (t)
k 0
f1(t - kT)u(t - kT)
L[ f (t)]
k 0
e-skT F1(s)
F1(s) 1- e-sT
Re(s) 0
例：求如图所示周期方波的Laplace变换。
f(t) 1
01
2345 周期方波信号
L[u(t) - u(t -1)] 1- e-s s
F(s) 1- e-s s
1 1- e-2s
1 s(1 e-s )
若
f (t) L F (s) Re( s) s 0
则有 f (at) L 1 F ( s ) aa
a 0, Re( s) as 0
L[ f (t)]
0-
f (at)e-st dt
1 a 0-
f
-st
(t)e a dt
1
F(

f
-st
(t)e a dt

1
F(
s
)
aa
收敛域：
Re(s/a) s0 Re(s) as0
3)时移特性（Time Shifting）
若 f (t) L F (s) Re( s) s 0
则有 f (t - t0 )u(t - t0 ) L e-st0 F (s) t0 0, Re(s) s 0
例：求信号f
(t)

sin 0
t
0 t 其它

的Laplace变换。
f (t) sin(t)u(t) sin(t - )u(t - )
F
(
s)

1 s2
e - s 1
Re(s) -
例：单边周期信号的Laplace变换。 f(t)
单边周期信号的定义：
f(t)=f(t+nT); t0, n=0,1,2,...
拉普拉斯变换 (the Laplace Transform)
1、从傅里叶变换到拉普拉斯变换
傅里叶分析具有清晰的物理意义，但某些信号的傅里 叶变换不存在 (t<0,无意义的函数)。引入拉普拉斯变换， 从而也可以对这些信号进行分析。拉普拉斯变换实质 是将信号f(t)乘以衰减因子e-s t的傅里叶分析。
L[cos(w0t)u(t)]
s
s2

w
2 0
Re(s) 0
L[sin(w0t)u(t)]
w0
s2

w
2 0
Re(s) 0
单边拉普拉斯的基本性质 (properties of Laplace Transform)
1 ) 线性特性(linearity)

17
若 x(t ) 是右边信号,即 T 则有
t , 0 在ROC内，
绝对可积，即：
x(t )e
0t

T

T
x(t )e
0t
dt
若1
0 ，则
e


dt

T
x(t )e 1t dt
x(t )e e
( 1 0 )T 2 Re[ s] 1 此时 x(t ) 是双边信号。
26
27
作业5月8日
• 9.2 • 9.3 • 9.21（b）（h）
28
§9.3 拉氏反变换
The Inverse Laplace Transform
一. 定义： 由 X (s) x(t )e st dt

例2.反因果信号： x(t ) e at u(t )
X ( s ) e e dt e
at st
0
0
( s a )t
1 dt , Re[s] a sa
8
由以上例子，可以看出: 1. 拉氏变换与傅里叶变换一样存在收敛问题。并非 任何信号的拉氏变换都存在，也不是 S 平面上的任 何复数都能使拉氏变换收敛。 2.拉氏变换积分收敛的那些复数 S 的集合，称为拉
础可以用几何求值的方法从零极点图求得 X ( j ) 的特性。这在定性分析系统频率特性时有很大
用处。
34
作两个矢量 s 和 a ，则 1
矢量
X (s1 )
1.单零点情况： X ( s) s a 零点s a , 要求出 s s1 时的 X (s1 )，可以
X (s1 ) (s1 a)

设
其中， 为 的从零处开始取值的第一个周期， 使用第一个周期函数依次向右平移并相加，则组 成单边周期函数： 利用时移性有：
例： 试求图中不同的时移对应变换 解：观察图形的时移关系，有如下对
x1 (t )
应变换：
0
t
x2 (t )
x1 (t ) ktu (t ) x2 (t ) k (t t0 )u(t ) x3 (t ) ktu(t t0 ) x4 (t ) k (t t0 )u(t t0 )
1 , 解: 由于 u (t ) s
L
0 sin 0tu (t ) 2 s 0 2 1 s L e 根据时移性质有： u (t 1) s
L
再根据频移性质有：
e
t
0 sin 0tu (t ) ( s ) 2 0 2
L
1 ( s 1) e u (t 1) e s 1
4.1 拉普拉斯变换
4.1.1 拉普拉斯变换定义
f (t)=eatu(t) a>0 的傅里叶变换？ 将f (t)乘以衰减因子e-t，得： 不存在!
令
若 ，则有
推广到一般情况：
（s= +j）
定义：
求傅里叶逆变换
拉普拉斯正变换 原函数
拉普拉斯逆变换 原函数
拉普拉斯变换符号表示及物理含义：
频域卷积
初值定理 终值定理
拉氏变换性质
1.线性
2.时移性
(1) 右移性 即指平移项右移，否则，依据单边变换定义，就 会把横轴左边部分截去，就不满足时移性了。因此，
时移性质准确是指右移性。
例如：求下面各式的单边拉普拉斯变换
解：前两项的单边变换相同，只需把三角函数按 三角公式展开，再利用基本变换求解，最后一项

[
f1 (t )
f2 (t)]
1 2
j
[F1(s)
F2 (s)]
=
1 2
j
j
j F1( p)F2 (s p)dp
3. 拉普拉斯逆变换 （1） 部分分式展开法
首先应用 海维赛展开定理将 F (s) 展开成部分分式，然后将各部分分式逐项进行逆变换，
最后叠加起来即得到原函数 f (t) 。
（2）留数法
1
1s s2
1 es 1 es
2
本文例 4-3下载后请自行对内容图4-2编（c） 辑修改删除，
应用微分性质求图 4-3（a）中 f1t , f2 (t), f3t 的象函数下面说明应用微分性质应注意的
问题，图 4-3（b）f1t , f2 t, f3t是的导数f1t , f2t , f3t 的波形。
1 t estd t 2 2 t estd t
0
1
1
t 1 est 1 1 estd t 2 1 estd t 2 t estd t
s
0
s 0
0
1
1 es s
1 s2
es
1 s2
2 e2s s
2 es s
2 e2s s
1 s2
es
1 s2
1 es
2
方法二：利用线性叠加和时移性质求解 由于
F
(s) 则 [ df (t)] dt
sF (s)
f (0 )
[
d
nf dt
(t)
n
]
sn
F
(s)
n1 r0
s n r 1
f
(r
)
(0
)
式中

−σt
指数增长信号
e
at
(a > 0)
e .e
at
−σt
(σ > a )
功率型周期信号
2
x1 (t ) = x(t )e
象函数 正LT
−σ t
s =σ + jω
X1 (ω) = ∫ x(t )e
−∞
∞
−(σ + jω )t
dt
双边拉普拉 斯变换
X (s) = ∫ x(t)e dt
−st −∞
∞
原函数 逆LT
3、拉氏变换的基本性质（1）
线性
∑k x (t)
i=1 i i
n
∑ k .L[ x(t )]
i =1 i
n
微分 积分
dx(t ) dt
sX ( s ) − x(0 )
X ( s ) x ' (0− ) + s s
−
∫
t −∞
f (τ ) d τ
时移 频移
x (t − t0 )u (t − t0 )
− 7e
−5t
)u (t )
16
6、单边拉普拉斯变换
实际信号一般都有初始时刻，不妨把初始时 刻设为坐标原点，通常大家关心的信号都是 x(t ) = 0, t < 0 的因果信号
X ( s ) = ∫ − x(t )e dt
− st 0
∞
称为信号x(t)的单边拉普拉斯变换
积分下限取0-是 为了处理在t=0 包含冲激函数及 其导数的x(t)时 较方便
dt
∫
x (t ) e
− st
dt
24
收敛域包含jω轴 。只要将Xb(s)中的s代以 jω ，即为信号的傅立叶变换

第五章 拉普拉斯变换
基本内容： 拉斯变换的定义(重点 重点)； 基本内容： 1. 拉斯变换的定义 重点 ； 2. 收敛域的概念(难点 ； 收敛域的概念 难点)； 难点 3. 零极点图； 零极点图； 4. 拉斯变换的性质 重点) ； 拉斯变换的性质(重点 重点 5. 系统函数 难点) ； 系统函数(难点 难点 6. 单边拉斯变换 重点)； 单边拉斯变换(重点 ； 重点
e
st
LTI
h (t )
∞ −∞
y (t ) = H ( s )e st
H ( s ) = ∫ h(t )e dt
定义: 定义
∞ X ( s ) = ∫−∞ x(t )e− st dt = LT {x(t )}
− st
5.1 拉普拉斯变换
一. 定义
e
st
LTI
h (t )
∞ −∞
y (t ) = H ( s )e st
−σ t ∞
f (t )e
−σ t
= FT {F (σ + jω}
−1
1 ∞ + jω t = ∫−∞ F (σ + jω )e dω 2π 1 ∞ (σ + jω t ) f (t ) = dω ∫−∞ F (σ + jω )e 2π 1 σ + j∞ st = ∫σ − j∞ F ( s )e ds 2π
5.4 复频域分析
5.4 复频域分析
5.4 复频域分析
5.4 复频域分析
5.4 复频域分析
5.4 复频域分析
5.4 复频域分析
应用举例： 应用举例： 图示电路，开关动作前已进入稳态， 例 1 ：图示电路，开关动作前已进入稳态，试 求开关打开后电感支路电流和电感两端电压。 求开关打开后电感支路电流和电感两端电压。 解： t<0，开关k闭合，电路稳定，有 ，开关 闭合 电路稳定， 闭合，

f (0+ ) = f0 (0+ ) = limsF (s) 0
s→∞
下面证明上式的 正确性 设对于F(s)长除后有
F(s) = Kmsm + Km−1sm−1 +⋯+ K0 + F (s) 0
式中F0(s)是真分式.对上式取逆变换
f (t) = Kmδ (t) + Km−1δ
m
m−1
(t) +⋯+ K0δ (t) + f0 (t)
第三章 拉普拉斯变换
§3.1 拉普拉斯变换
一 拉普拉斯变换的定义及收敛域 ①定义 双边拉普拉斯变换对
∞ F(s) = ∫ f (t)e−st dt −∞ σ + j∞ 1 F(s)est ds f (t) = 2 j ∫ − j∞ π σ
其中， = σ + jω 称为复频率，s平面为复平面。 s
−a < Re(s) < a
由上式可以看出，X(s)没有零点，在 s=a 和 s=-a 处 有两个极点，如下图
-a
a
如果 a<0， 1）式和（2）式的收敛域不重叠，没有公共的 （ 收敛域，因此，x(t)的拉氏变换不存在。
§3.2 拉氏变换的基本性质
• 线性
a1 f1(t) + a2 f2 (t) ⇒ a1F (s) + a2F2 (s) 1
• 尺寸变换 • 时间平移 • 频率平移
f (t)es0t ⇒ F(s − s0 )
1 f (at) ⇒ F(s / a) a
f (t − t0 )u(t − t0 ) ⇒ F(s)e−st0
• 时域微分
df (t)/ dt ⇒ sF(s) − f (0− )

拉普拉斯变换基本要求拉普拉斯变换的定义、收敛域的概念：熟练掌握拉普拉斯变换的性质、卷积定理的意义及它们的运用。

能根据时域电路模型画出S 域等效电路模型，并求其冲激响应、零输入响应、零状态响应和全响应。

能根据系统函数的零、极点分布情况分析、判断系统的时域与频域特性。

理解全通网络、最小相移网络的概念以及拉普拉斯变换与傅里叶变换的关系。

会判定系统的稳定性。

知识要点1. 拉普拉斯变换的定义及定义域 （1） 定义 单边拉普拉斯变换： 正变换0[()]()()stf t F s f t dt e ζ∞--==⎰逆变换1[()]()()2j stj F s f t F s ds j e σσζπ+∞-∞==⎰双边拉普拉斯变换： 正变换()()stB s f t dt e F ∞--∞=⎰逆变换1()()2j stB j f t s ds j e F σσπ+∞-∞=⎰（2） 定义域若0σσ>时，lim ()0tt f t eσ-→∞=则()tf t eσ-在0σσ>的全部范围内收敛，积分0()stf t dte +∞--⎰存在，即()f t 的拉普拉斯变换存在。

0σσ>就是()f t 的单边拉普拉斯变换的收敛域。

0σ与函数()f t 的性质有关。

2. 拉普拉斯变换的性质 （1） 线性性 若11[()]()f t F S ζ=,22[()]()f t F S ζ=,1κ,2κ为常数时，则11221122[()()]()()f t f t F s F s ζκκκκ+=+（2） 原函数微分 若[()]()f t F s ζ=则()[]()(0)df t sF s f dtζ-=- 式中()(0)r f-是r 阶导数()r rd f t dt在0-时刻的取值。

（3） 原函数积分 若[()]()f t F s ζ=，则(1)(0)()[()]tf F s f t dt s sζ---∞=+⎰式中0(1)(0)()ff t dt ---∞=⎰（4） 延时性若[()]()f t F s ζ=，则000[()()]()st f t t u t t e F s ζ---=（5） s 域平移若[()]()f t F s ζ=，则[()]()atf t e F s a ζ-=+（6） 尺度变换若[()]()f t F s ζ=，则1[()]()sf at F a aζ=（a >0） （7） 初值定理lim()(0)lim ()t o s f t f sF s ++→→∞==（8） 终值定理lim ()lim ()t s f t sF s →+∞→∞=（9） 卷积定理若11[()]()f t F s ζ=，22[()]()f t F s ζ=，则有1212[()()]()()f t f t F s F s ζ*=12121[()()][()()]2f t f t F s F s jζπ=*=121()()2j j F p F s p dp j σσπ+∞-∞-⎰3. 拉普拉斯逆变换 （1） 部分分式展开法首先应用海维赛展开定理将()F s 展开成部分分式，然后将各部分分式逐项进行逆变换，最后叠加起来即得到原函数()f t 。

第四章 拉普拉斯变换—连续信号s 域分析一、考试内容（知识点）1．拉普拉斯变换的定义及其性质、拉普拉斯逆变换； 2．系统的复频域分析法； 3．系统函数)(s H ；4．系统的零极点分布决定系统的时域、频域特性； 5．线性系统的稳定性；6．拉普拉斯变换与傅里叶变换之间的关系。

二、内容（知识点）详解1．拉普拉斯变换的定义、收敛域（1）变换式与反变换式dt e t f t f s F st -∞⎰-==0)()]([)(L ds e s F js F t f stj j ⎰∞+∞--==σσπ)(21)]([)(1L )(s F 称为)(t f 的象函数，)(t f 称为)(s F 的原函数。

下限值取-0，主要是考虑信号)(t f 在t =0时刻可能含有冲激函数及其导数项也能包含在积分区间之内。

（2）收敛域在s 平面上，能使式0)(lim =-→∞t t e t f σ满足和成立的σ的取值范围（区域），称为)(t f 或)(s F 的收敛域。

2．常用时间函数的拉普拉斯变换（1）冲激函数 )()(t t f δ= 1)(=s F)()()(t t f n δ= n s s F =)(（2）阶跃函数 )()(t u t f = ss F 1)(= （3）n t （n 是正整数） t t f =)( 21)(s s F =2)(t t f = 32)(s s F =n t t f =)( 1!)(+=n s n s F（4）指数信号 t e t f α-=)( α+=s s F 1)(t te t f α-=)( ()21)(α+=s s F t n e t t f α-=)( ()1!)(++=n s n s F αt j e t f ω-=)( ωj s s F +=1)( （5）正弦信号、余弦信号系列)sin()(t t f ω= 22)(ωω+=s s F)cos()(t t f ω= 22)(ω+=s ss F)sin()(t e t f t ωα-= 22)()(ωαω++=s s F)cos()(t e t f t ωα-= 22)()(ωαα+++=s s s F )sin()(t t t f ω= 222)(2)(ωω+=s ss F )cos()(t t t f ω= 22222)()(ωω+-=s s s F )()(t sh t f ω= 22)(ωω-=s s F )()(t ch t f ω= 22)(ω-=s ss F （6） ∑∞=-=0)()(n nT t t f δ sT e s F --=11)(∑∞=-=00)()(n nT t f t f sTes F s F --=1)()(0 3．拉普拉斯变换的基本性质象函数)(s F 与原函数)(t f 之间的关系为：)]([)(t f s F L = （1）线性（叠加性）∑∑===⎥⎦⎤⎢⎣⎡ni i i n i i i s F a t f a 11)()(L ，其中i a 为常数，n 为正整数。